李金楠， 高 翔

(中国海洋大学数学科学学院， 山东 青岛 266100)

20世纪80年代，Hamilton[1]引进了Ricci孤立子的概念，Ricci孤立子是爱因斯坦度量的自然推广且为解决三维庞加莱猜想的主要工具。同时Ricci孤立子对应于Ricci流的自相似解[2-3]且出现在Ricci流方程的奇异点经伸缩变换后的极限中[4-6]。

黎曼度量gij为爱因斯坦度量若其Ricci张量满足：

Rij=ρgij，

式中ρ为常数。特别地，具有爱因斯坦度量的光滑流形称为爱因斯坦流形。

光滑流形Mn上的一个完备黎曼度量gij称为Ricci孤立子，若存在一个光滑向量场V=(Vi)使其Ricci张量满足：

式中ρ为常数。此外，若V为一个梯度向量场，则有梯度Ricci孤立子满足方程：

Rij+▽i▽jf=ρgij。

式中f为流形Mn上的光滑函数，称f为Ricci孤立子的势函数。由于常数ρ取值不同，所以可将Ricci孤立子进行分类，其中ρ=0称为稳定Ricci孤立子，ρ>0称为收缩Ricci孤立子，ρ<0称为扩张Ricci孤立子。

爱因斯坦流形是梯度Ricci孤立子势函数为常数的特例，也称为平凡孤立子，可见势函数对于Ricci孤立子的分类具有十分重要的作用。此外结合余面积公式与势函数估计还可进一步给出孤立子的体积增长估计，并最终应用于研究孤立子的分类问题。因此研究Ricci孤立子的势函数估计对孤立子的分类及其他几何不变量的研究都具有十分重要意义。

Bakry-Emery Ricci张量定义为：

Ricf=Ric+Hessf。

Bakry-Emery[7]对该张量进行了详细研究并拓展应用解决了许多重要的孤立子问题。特别地，当势函数f为常数时，Bakry-Emery Ricci张量即为Ricci张量，因此很多关于Ricci张量的性质及结果可以自然地推广到Bakry-Emery Ricci张量上。本文我们将主要证明一个关于Bakry-Emery Ricci张量的Ambrose 型结论，并得到一些Ricci孤立子势函数上下界更精确的估计结果。

1 预备知识

首先，关于流形的紧致性，Ambrose[8]证明了如下定理。

引理1设在完备黎曼流形M上存在点p使得任意从点p出发的测地线γ(t)满足：

则M为紧致的。

推广到Bakry-Emery Ricci张量，张世金[9]证明了对应的Ambrose-Myers型结果。

引理2设在完备黎曼流形(M,g,f)上存在点p使得任意从p出发的测地线γ(t)满足

且势函数满足

f(x)≤C(d(x,p)+1)，

式中C为常数，d(x,p)为从点p到点x的距离函数，则流形M为紧致的。

此外，张世金[9]还给出了以下结论。

引理3一个完备黎曼流形M若满足

Ricf≥λg

及

f(x)≤C(d(x,p)+1)，

式中λ>0，C为常数，则M为紧致的。

2 主要结果

改变势函数上界条件可将引理3进一步推广到Bakry-Emery Ricci张量上，因此我们给出以下定理：

定理1一个完备的黎曼流形(M,g,f)若其Bakry-Emery Ricci张量满足

Ricf≥-λg，

λ>0为常数，固定点p∈M，同时势函数f满足

f(x)≤-δ(d(x,p)+C)2，

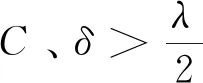
应用上述结果并结合孤立子性质[10-11]，将得到一些梯度Ricci孤立子的势函数上下界估计结果。

定理2令(Mn,gij,f)为一个具有非负Ricci曲率的完备非紧致扩张梯度Ricci孤立子，标准化满足

则其势函数f满足估计：

式中r(x)=d(x,p)为点x到固定点p∈M的距离函数；C为仅取决于维数n及单位球Bp(1)的度量gij的常数。

结合Bakry-Emery Ricci张量，张世金[9]还给出了有关收缩Ricci孤立子的经典势函数下界估计结果[10]，利用本文结论可给出该结论的其他证明方法。

推论1令(Mn,gij,f)为一个完备非紧致的收缩梯度Ricci孤立子且

则势函数f满足：

式中：r(x)=d(x,p)为距离函数；C>0为仅取决于流形的维数n及单位球Bp(1)的度量gij的常数。

同理，推广到稳定梯度Ricci孤立子，将得到以下推论。

定理3令(Mn,gij,f)为一个具有正Ricci曲率的完备非紧致稳定梯度Ricci孤立子，则其势函数f满足下界估计：

f(x)≥-C(r(x)+1)。

式中：r(x)=d(x,p)为距离函数；C>0为仅取决于维数n及单位球Bp(1)的度量gij的常数。

3 主要方法及证明

本节将推广利用Wraith[12]的方法给出满足Bakry-Emery Ricci张量下界为负常数主要定理的证明。

定理4一个完备黎曼流形(M,g,f)若满足

Ricf≥-λg，

λ>0为常数，同时固定点p∈M，势函数f满足

f(x)≤-δ(d(x,p)+C)2，

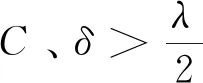
证明 (反证法)设黎曼流形M为非紧致的，固定点p∈M及单位速度射线γ(t)，γ(t)满足初始条件γ(0)=p(即测地线γ(t)从点p出发)。任意时间t，令m(t)为以点γ(t)为中心、以t到p的距离为半径的距离球面的平均曲率，这里以单位内法向量计算平均曲率。值得注意的是，对任意射线γ(t)，t>0时函数m(t)为光滑的，且Wraith[12]证明m(t)满足 Riccati不等式：

代入即Bakry-Emery Ricci张量满足：

由于

[▽f,γ′](t)-[▽f,γ′]。

由假设Ricf≥-λg，故对任意时间t>1，有

-λ(t-1)-m(1)+[▽f,γ′]。

令C1=λ-m(1)+[▽f,γ′](1)，上述不等式为

另外，由定理假设f(x)≤-δ(d(x,p)+C)2可知f(γ(t))≤-δ(t+C)2，则

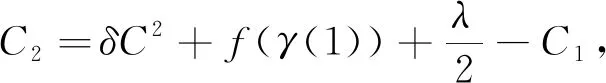
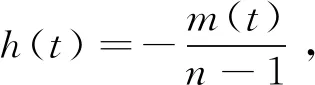
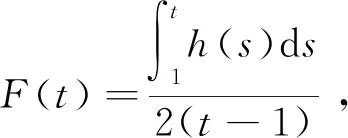
则任意t≥t1>3，有

接下来令

tn+1=tn+21-n，(n≥1)，则对任意i≥1，ti∈

[t1,t1+2)。

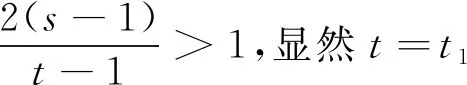
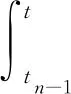
由数学归纳法可知，对任意t∈[tn,t1+2)有F(t)≥2n。

又对任意时间t∈[t1,+∞)，函数F(t)为光滑的，故

矛盾，综上定理4得证。

4 应用

应用定理4并结合不同的Ricci孤立子方程条件，本节将主要采用定理2的结果对梯度扩张Ricci孤立子的势函数估计进行证明并简要介绍稳定及收缩Ricci孤立子的情况。

对于梯度扩张Ricci孤立子，张珠洪[13]已给出其势函数上下界估计的相关结果，本节我们将结合Bakry-Emery Ricci张量及定理4的结论采用不同的方法给出其势函数的一个下界估计。

定理5令(Mn,gij,f)为一个具有非负Ricci曲率的完备非紧致扩张梯度Ricci孤立子，孤立子方程满足

则其势函数f满足估计：

式中：r(x)=d(x,p)为点x到固定点p∈M的距离函数；C为仅取决于维数n及单位球Bp(1)的度量gij的常数。更准确的说，常数C满足

固定点p∈M及单位速度射线γ(t)，由Riccati 不等式可得

特殊的，当Ricf=-λg，则任意时间t>1满足

-λ(t-1)-m(1)+[▽f,γ′]。

令C1=λ-m(1)+[▽f,γ′](1)，上述不等式为

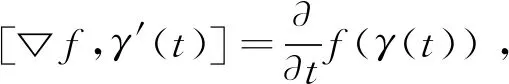
由定理假设势函数

显然有

代入上式得

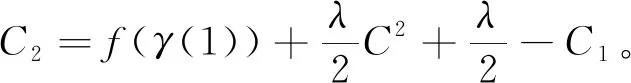
存在t1>3，对任意t≥t1，令常数C满足

有

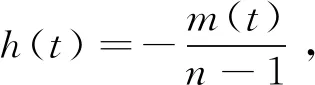
接下来的证明同定理4，可得矛盾，即证明了当势函数满足上界估计

时定理4也成立。

作为应用，令

故对于非紧致扩张梯度Ricci孤立子，存在仅取决于维数及黎曼度量的常数C使得

综上定理得证。

注：上述定理推广到非紧致稳定梯度Ricci孤立子可得其势函数的一个上界估计。准确地说，若假设Bakry-Emery Ricci张量Ricf≥0，势函数f(x)≤-C(r(x)+1),则存在常数C,当C≥6n-[▽f,γ′](1)-m(1)时，定理1成立。

特别地，Ricf=0(即(Mn,gij,f)为稳定Ricci孤立子)，自然可以证明曹怀东等[11]给出的经典的势函数估计结果。

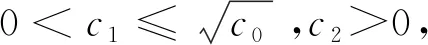
式中r(x)=d(x0,x)为点x到固定点x0∈M的距离函数，常数c0=Rmax满足R+|▽f|2=c0。

此外，由定理1的证明显然有如下推论。

推论2完备黎曼流形M若满足Ricf≥0及f(x)≤-Cd2(x,p)，常数C>0，则M为紧致的。