时统业，曾志红

（1.海军指挥学院，江苏 南京 211800；2.广东第二师范学院学报编辑部，广东 广州 510303）

0 引 言

1938 年，Ostrowski［1］证明了著名的不等式

Ostrowski不等式理论在近似理论、概率论和数值积分中有着广泛应用 .自 1975 年 Milovanović［2］给出式（1）的推广以后的几十年来，学者们建立了涉及各种类型积分、各种类型的凸函数、各种空间、高阶导数、权函数和带有扰动的Ostrowski型不等式，有关Ostrowski不等式的改进和推广见文献［2-11］.

2002年，通过建立带有Peano型核的Montgomery 型积分恒等式（下面的引理 1），Cerone［12］建立了一类新的Ostrowski型不等式，与其他文献不同的是，给出了f(x)与覆盖区间[a，b]的区间[a，x]，[x，b]上的函数平均值的加权算术平均的偏离的界.

引理 1［12］设f：[a，b]→ R 是绝对连续函数，则对任意的和任意x∈ (a，b)有

定理 1［12］设是绝对连续函数，且则对任意的和任意x∈ (a，b)有

Qayyum等［13］通过建立带有Peano型核并带有参数的涉及一阶导数的Montgomery型积分恒等式，给出式（2）的推广；Qayyum等［14］通过建立带有加权Peano型核的涉及一阶导数的Montgomery型积分恒等式，给出式（2）的加权推广；Qayyum 等［15］通过建立涉及二阶导数的积分恒等式（下面的引理2），在二阶导函数有界的情况下，得到式（2）的带有扰动的推广.

引 理 2［15］设二 阶 可 微 ，且f″在[a，b]上 可 积 ，则 对 任 意 的λ∈[0，1]和 任 意x∈ (a，b)有

定理 2［15］设二阶可微，且则 对 任 意 的和 任 意x∈ (a，b)有

Qayyum等［16］又把式（2）和（3）推广到n阶可微函数；Alshanti［17］通过建立新的带有加权 Peano 型核的积分恒等式，在二阶导函数有界的情况下又对式（3）作 了 加 权 推 广 ；Qayyum 等［18］通 过 建 立 带 有Peano型核并带有参数的涉及二阶导数的Montgomery型积分恒等式，给出式（3）的推广；Qayyum等［19］又把这个结果推广到n阶可微函数；Jiang等［20］还将式（2）推广到时间尺度上.

本文将借助引理1和2中的积分恒等式，仿照Cheng 和 Sun［21］有关引入参数求最值的方法，在式（2）和（3）的右边都减去了一个非负项，给出式（2）和（3）的加强.为方便起见，引入记号

1 主要结果

因为f是绝对连续函数，且∞，所以也是绝对连续函数，且应用已证结论，则式（4）的左边不等式得证.

推论1设条件同定理3，则对任意的和任意的x∈(a，b)有

推论2设条件同定理3，则对任意的x∈(a，b)有

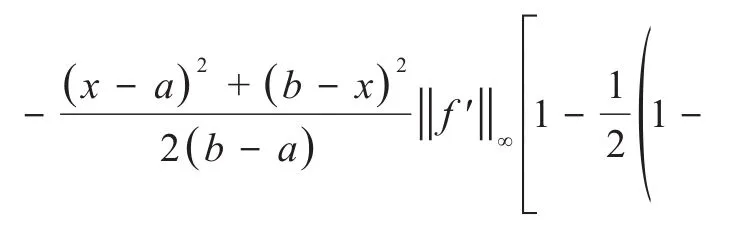
从而有Ostrowski不等式的加强：

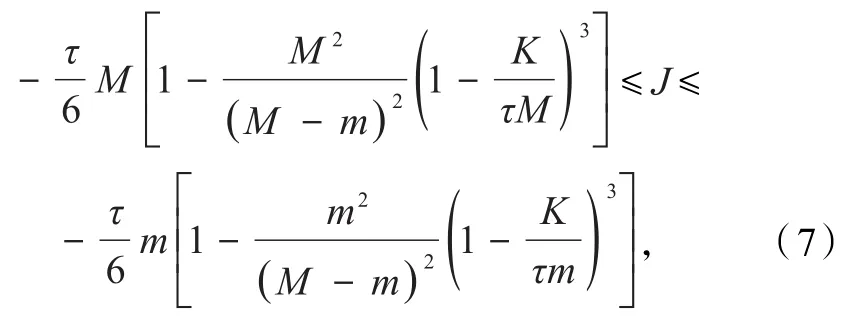
其中

推论4 设条件同定理4，则对任意的x∈(a，b)有

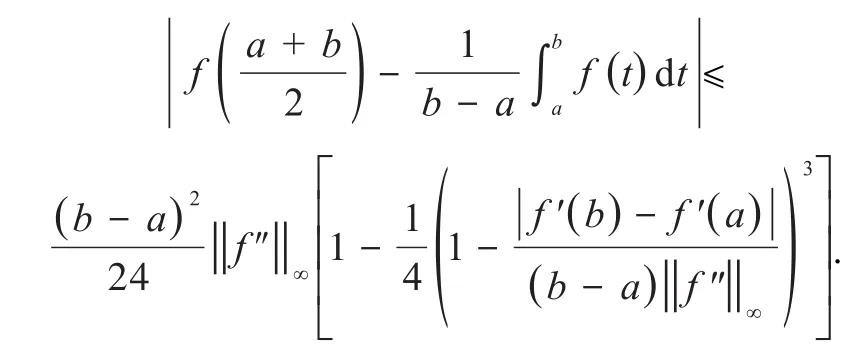
式（10）是式（3）的加强.

接下来的证明类似于定理4，故略去.

推论6设条件同定理5，则有式（9）成立.

推论 7设f：[a，b]→R可微，且f′满足M-Lipschitz条件，即存在常数M，使得对于任意t，s∈ [a，b]有则有

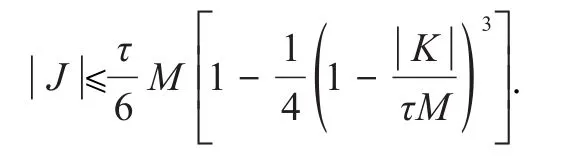
其中

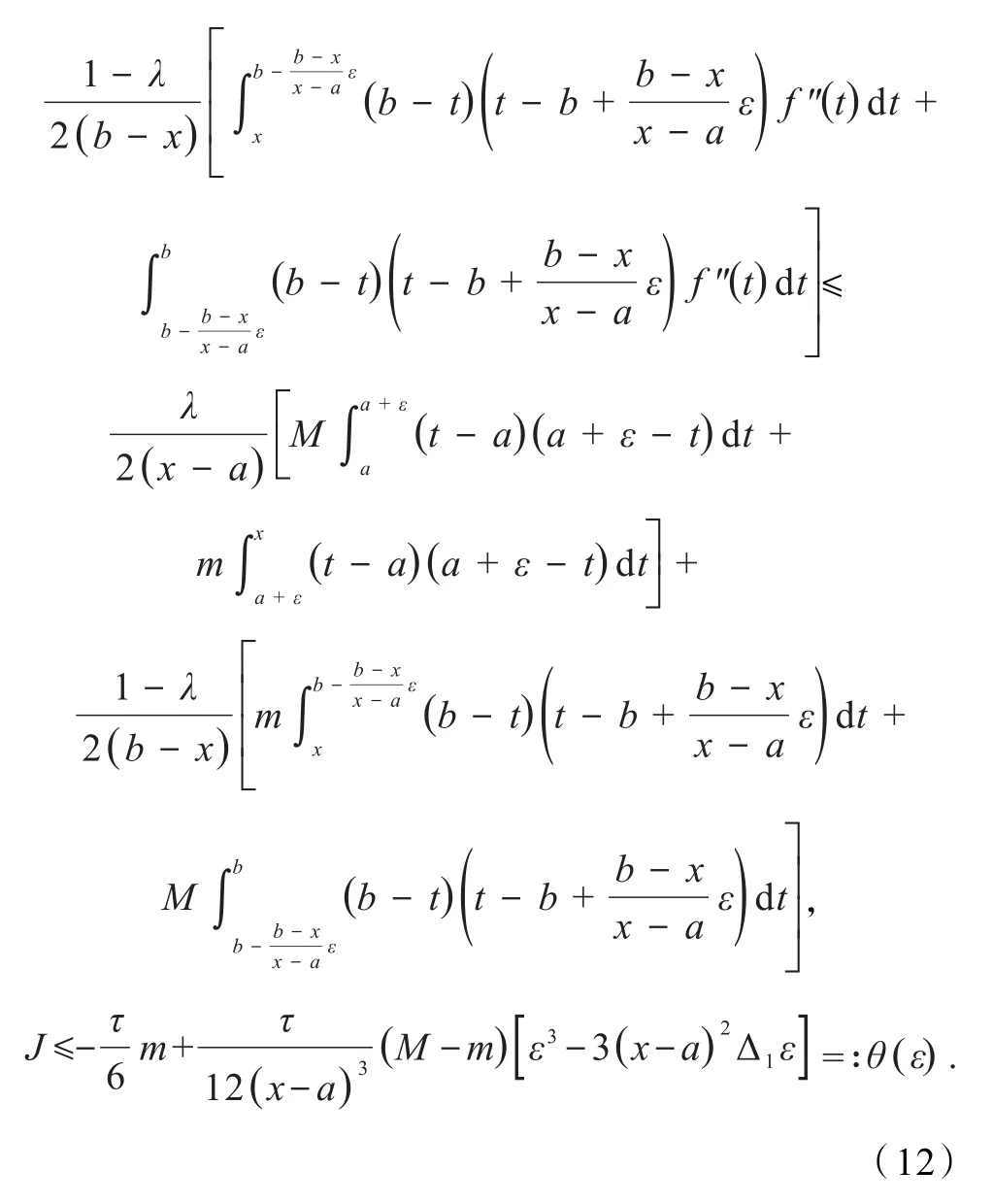
因为当m≤f″(t)≤M时，有对应用已证结论，则式（11）的左边不等式得证.

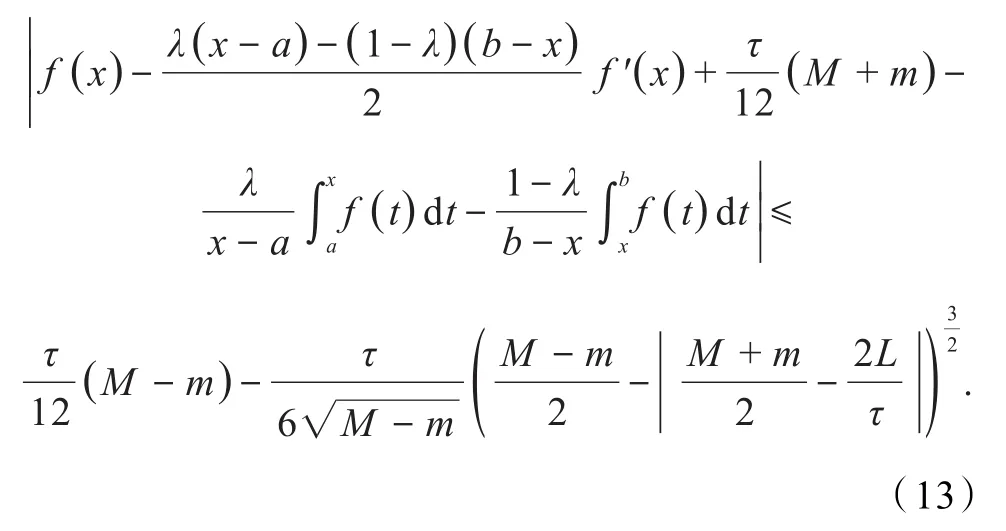
式（14）是式（3）的加强.

接下来的证明类似于定理6，故略去.

推论 11 设f：[a，b]→ R 可微，且f′满足M-Lipschitz条件，即存在常数M，使得对于任意t，s∈[a，b]有则对任意的和 任意的x∈ (a，b)有

2 结束语

本文加强了已有的利用一阶导数对函数值与覆盖整个区间的2个区间上函数平均值组合之差的估计结果，分别在二阶导数有界和一阶导数满足Lipschitz条件的情况下，给出已有扰动的结果的加强.用引入参数求最值的方法，还可以继续做对应于经典Ostrowski不等式的推广研究，将式（2）和式（3）推广到各种类型的积分，以及各种类型凸函数和各种空间等.