张练，刘小华，吴念，曾职云

（贵州民族大学 数据科学与信息工程学院，贵州 贵阳 550025）

非线性分数阶偏微分方程具有广泛而丰富的应用背景，又由于分数阶偏微分方程可以对复杂现象进行更精确的描述。如非布朗运动、信号处理、流体流动等领域中的许多现象都可以用分数阶偏数分方程来描述。自1834年苏格兰工程师Russell发现一种称为孤立波的非线性波以来，研究人员不断地深入研究，从而对非线性波的研究进入了一个新的时代。最近，对于分数阶非线性偏微分方程精确解的研究，产生了许多行之有效的方法,例如投设方法[1]、Jacobi椭圆函数展开法[2]、修正的试验方程法[3]、动力系统分支方法[4-5]等。改进的扩展辅助方程映射法是一种求解非线性偏微分方程行波解的有效方法，Lu Dianchen[6]等首次运用改进的扩展辅助方程映射法构造了广义ZK-BBM方程和改进的C-H方程的孤立波解，Aly R.Seadawy[7]等通过改进的扩展辅助方程映射法得到非线性扩散反应(DR)方程的精确行波解、孤立波解。

本文利用改进的扩展辅助方程映射法考虑如下的非线性时间分数阶Burger方程[8]的精确行波解,

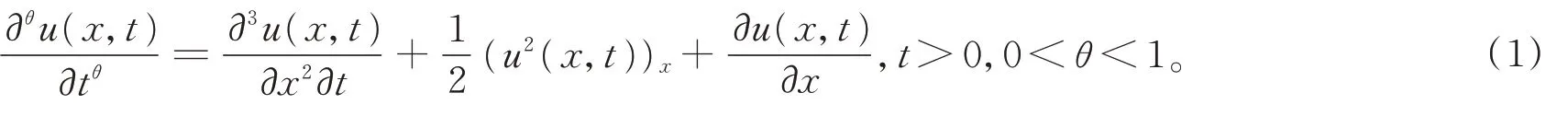
非线性时间分数阶Burger方程是黏性流体现象的一种模型，通过Cole-Hopf变换转化成线性化热方程，它是一类非常重要的非线性偏微分方程，Burger方程的行波解现已取得了许多重要的结果。赵昕,夏善磊[9]运用子方程法得出分数阶Burgers方程和mKdV方程的精确行波解；李晓峰,韩家骅[10]通过扩展的映射法得到了mKdV-Burgers方程的孤波解和周期波解；R.Saleh等[11]运用奇异流形法得出方程(1)的精确解。本文先对方程(1)进行分数复变换，将其转化为常微分方程，然后化为与之等价的平面动力系统，利用平面动力系统理论与方法进行定性分析，给出行波解的存在性，最后利用改进的扩展辅助方程映射法得出方程(1)新的孤立波解的精确表达式。

1 方程(1)有界行波解的存在性

对(1+1)维非线性时间分数阶Burger方程(1)做分数复变换[12]

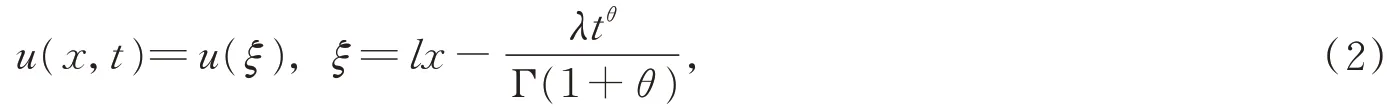
其中l,λ是任意非零常数，则将方程(1)转化为方程

对系统(4)进行首次积分得

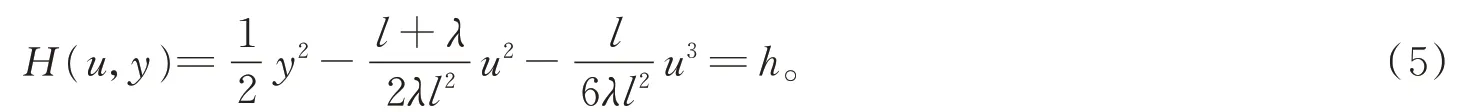
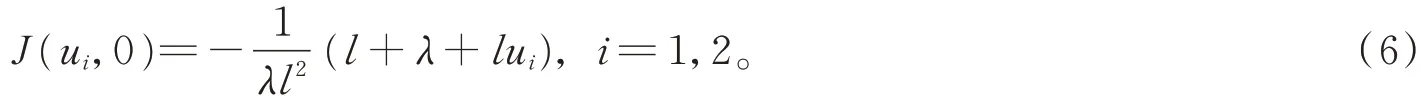
根据平面动力系统理论[13]可知，如果J(ui,0)<0,则为鞍点，如果J(ui,0)>0,则为中心，如果J(ui,0)=0,则为尖点。

当λ>0,l+λ>0时，(0,0)是鞍点，是中心；当λ>0,l+λ<0时，(0,0)是中心，是鞍点;

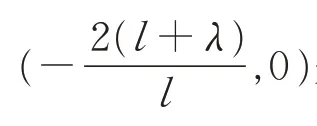
当λ<0,l+λ>0时，(0,0)是中心，是鞍点；当λ<0,l+λ<0时，(0,0)是鞍点，是中心;

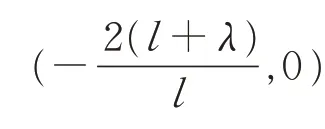
当λ≠0,l+λ=0时，是尖点。

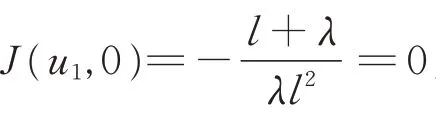
则据不同参数条件下系统(4)的相图如图1所示。

由平面动力系统理论与方法[13]可知，同宿轨对应着方程(3)的钟状孤波解，异宿轨对应着方程(3)的扭状孤波解，闭轨对应着方程(3)的周期解。因此根据图1中的(a)~(e)的轨线可知，方程(3)的有界行波解的存在性结论为：

(1)系统(4)在λ>0,l+λ>0时，方程(3)存在一个钟状孤波解u(ξ),(u(ξ)→0,ξ→±∞)和无穷多个周期解(见图1(a))。

(2)系统(4)在λ>0,l+λ<0时，方程(3)存在一个钟状孤波解和无穷多个周期解(见图1(b))。

(3)系统(4)在λ<0,l+λ>0时，方程(3)存在一个钟状孤波解和无穷多个周期解(见图1(c))。

(4)系统(4)在λ<0,l+λ<0时，方程(3)存在一个钟状孤波解u(ξ),(u(ξ)→0,ξ→±∞)和无穷多个周期解(见图1(d))。

(5)系统(4)在λ≠0,l+λ=0时，方程(3)存在有界行波解(见图1(e))。

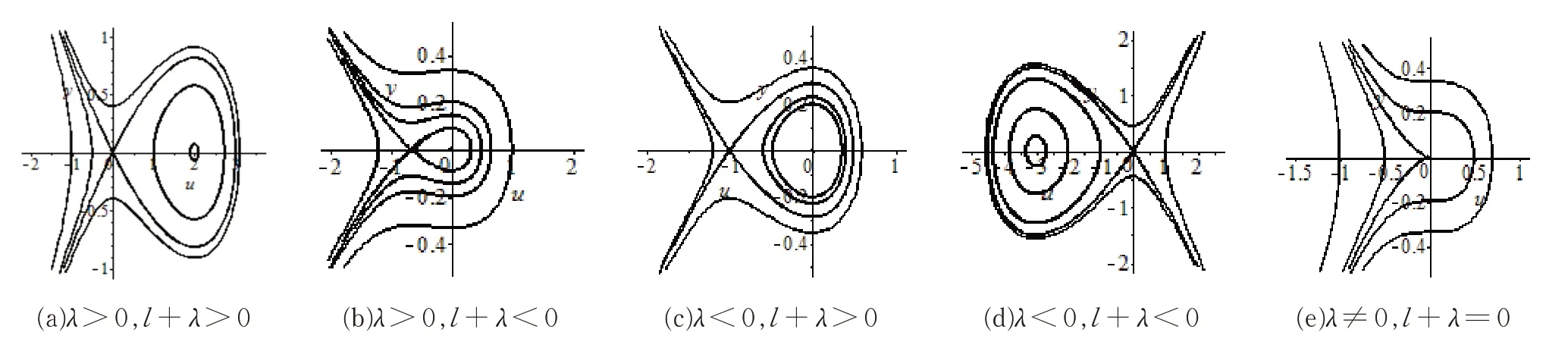
图1 系统(4)在不同参数条件下的相图

由上面的定性分析可知，方程(3)存在四个钟状孤波解、无穷多个周期解和有界行波解，上述得知方程(3)的解的个数与行波解类型，下面将运用改进的扩展辅助方程映射法讨论方程(1)新的精确孤立波解。

2 改进的扩展辅助方程映射方法

考虑如下形式的非线性偏微分方程：

其中P是包含u(x,t)及其它的各导数的多项式函数。

步骤1：对上述方程(7)做行波变换u(x,t)=u(ξ),ξ=lx+λt,其中l,λ是任意非零常数；将上述方程(7)转化为如下的常微分方程：

其中F是包含u(x,t)及其它的各导数的多项式函数。

步骤2：假设方程(8)有如下形式的解：

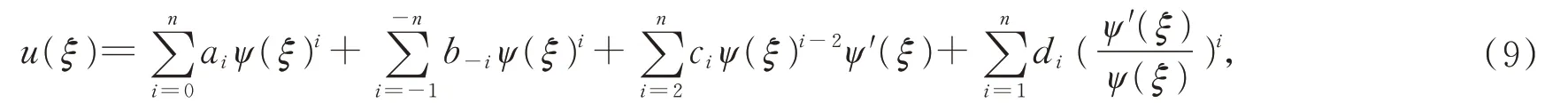
其中ai,bi,ci,di为待定系数，将在后面给出，n由齐次平衡原则确定；ψ(x),ψ′(x)满足如下常微分方程

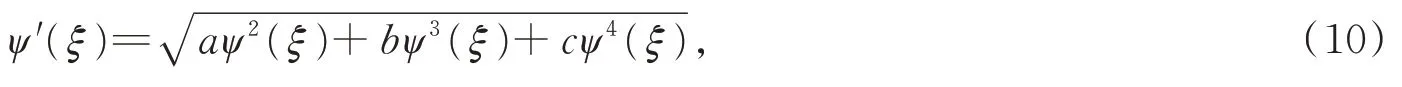
其中a,b,c是常实数，方程(10)的解见文献[14],在第3部分仅用其中孤立波形式的解。

步骤3：将方程(9),(10)代入方程(8),令ψi(ξ)ψ′j(ξ),(i=-n,-n+1,…,n-1,n;j=0,1)的每个多项式等于零，结合Maple软件解这个代数方程组，得到ai,bi,ci,di,l,λ的值。

步骤4：将步骤3得到的值与ψi(ξ)ψ′j(ξ),(i=-n,-n+1,…,n-1,n;j=0,1)代入假设(9),从而得到方程(8)的解，又根据行波变换进而可得方程(7)的有界行波解。

3 方程(1)的孤立波解的精确表达式

下面利用改进的辅助方程映射法来讨论方程(1)的孤波解，由方程(3)的最高阶导数项u″(ξ)与最高阶非线性项u2(ξ)的平衡原则,有n+2=2n得n=2,则可假设方程(3)的解有如下形式：

将(10)，（11）代入方程(3),合并ψi(ξ)ψ′j(ξ),(i=-4,-3,…,3,4;j=0,1)的同类项，并令每个代数方程组等于零，结合Maple软件解这个代数方程组，求得参数a0,a1,a2,b1,b2,c2,d1,d2,λ,a,b的值。下面情形中没有写出的a,λ为任意非零常数，,其中ξ0=0,根据参数的不同，得到7组不同情形如下：

情形1：

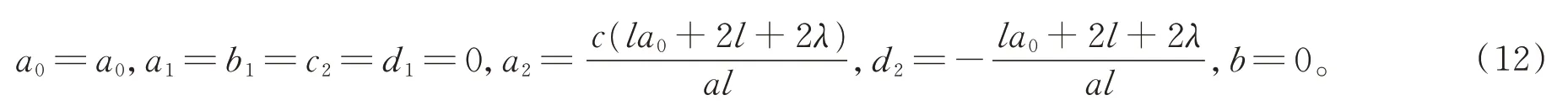
由（10）,(12)的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

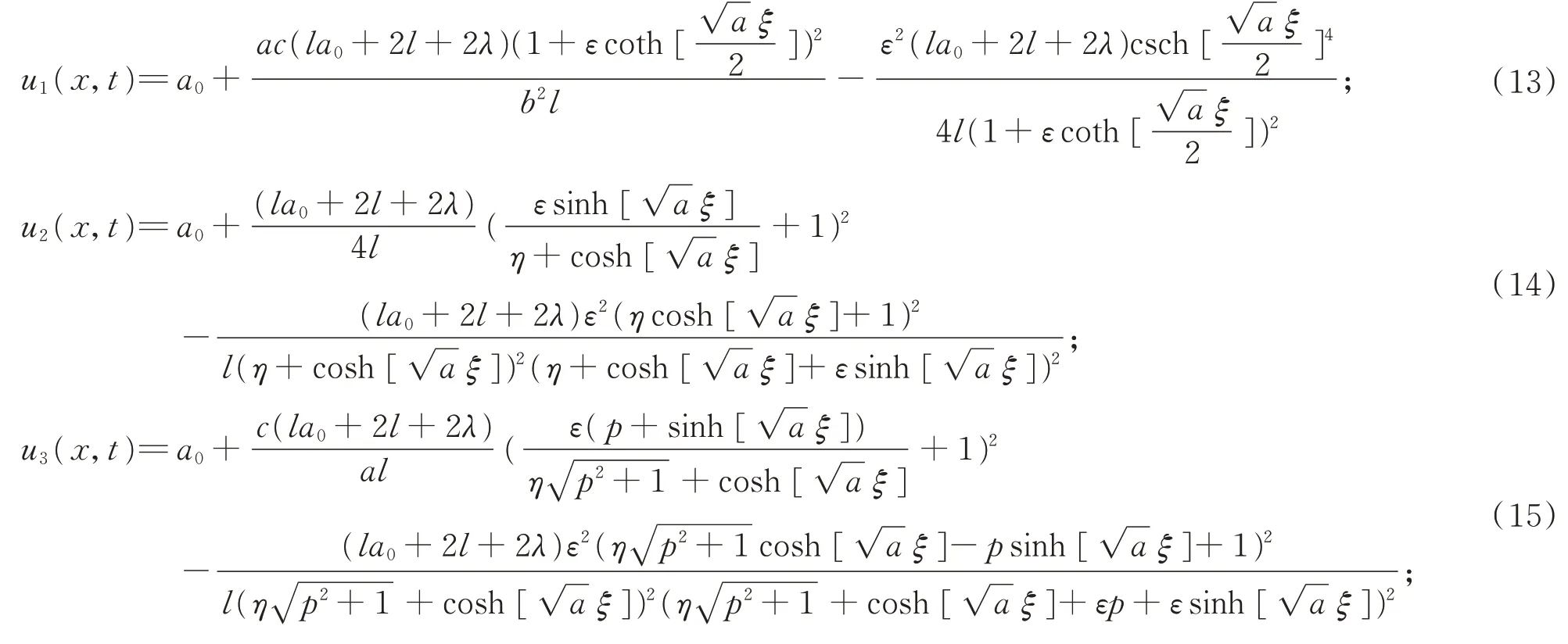
情形2:

由(10)，（16）的解代入假设(12)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

运用Maple软件得出(18)式解的平面图与三维图(图2)：,η=-2

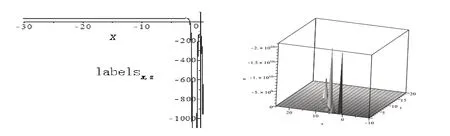
图2 其中ε=8,a=2,c=2,a0=2,l=1,λ=4,θ=

情形3：

由（10）,(20)的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

情形4：

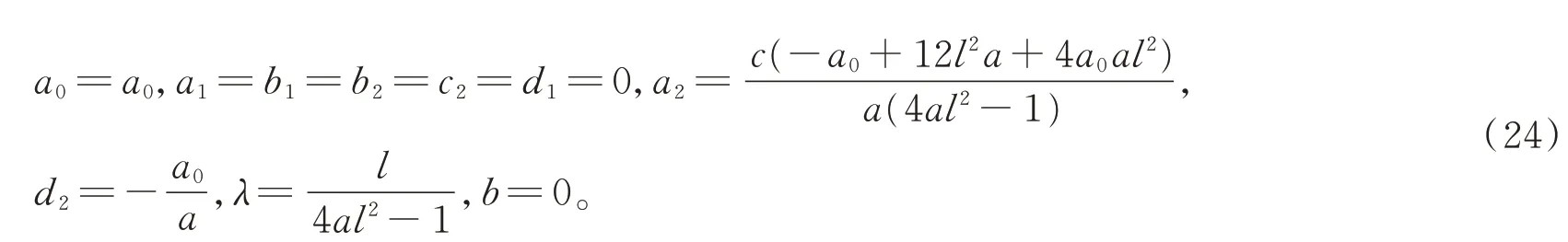
由(10),(24)的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

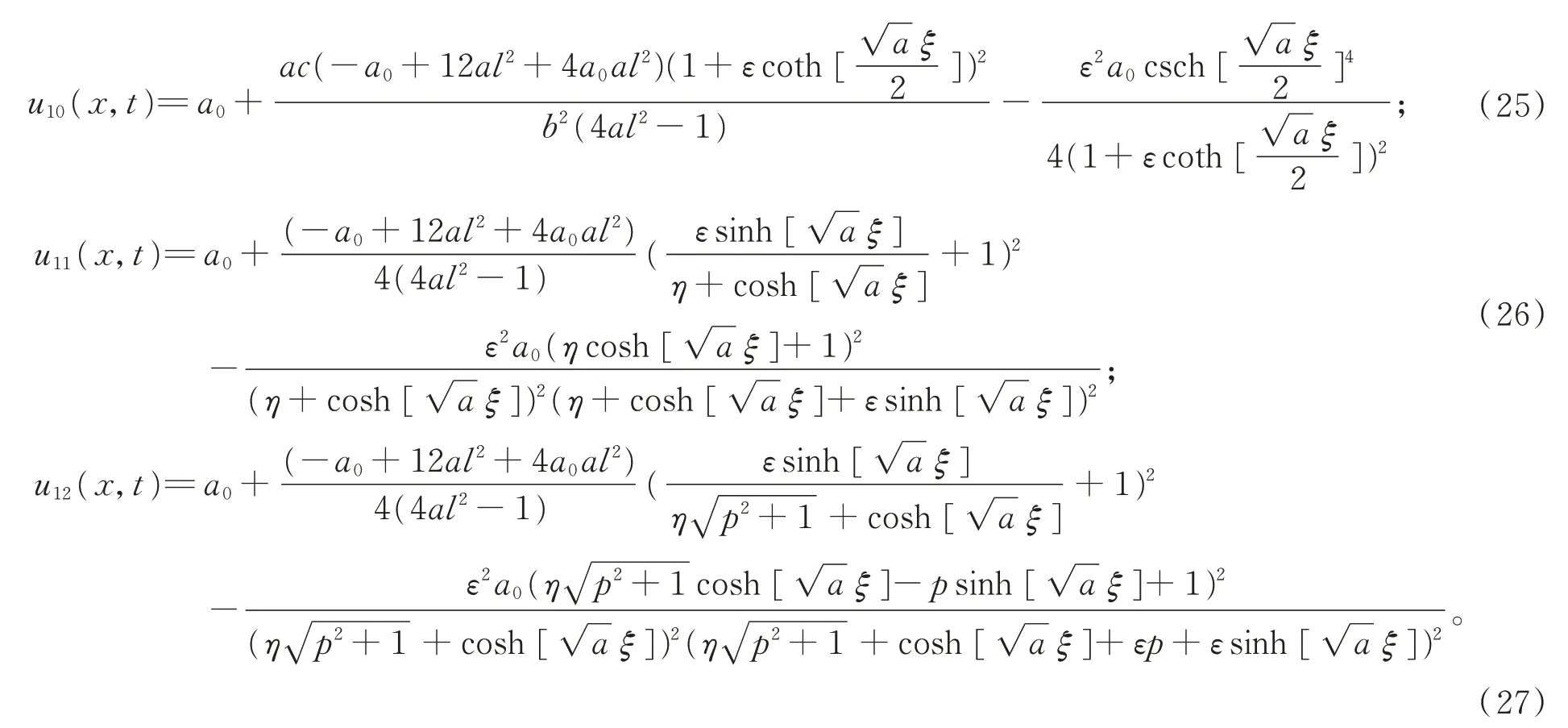
运用Maple软件得出(25)式解的平面图与三维图(见图3)：

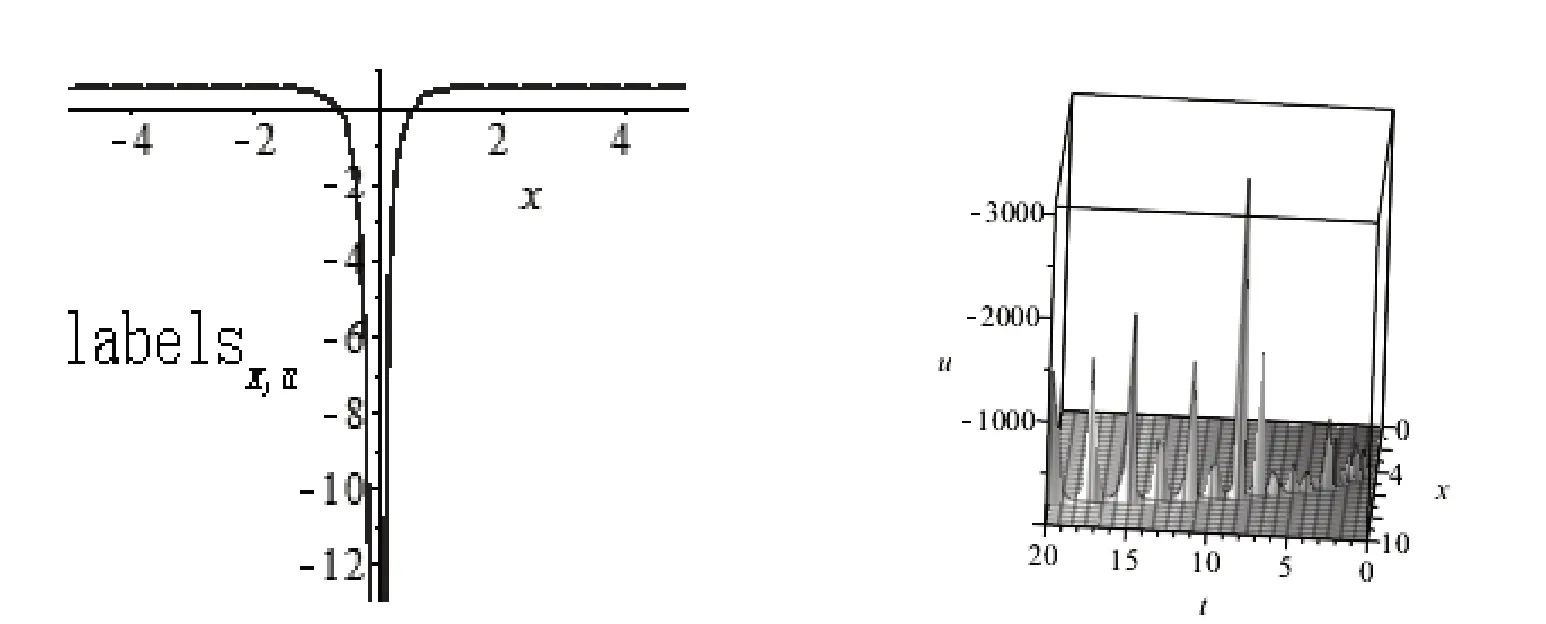
图3 其中取ε=8,a=2,c=2,b=0,a0=0.5357,l=1,λ=4,θ=

情形5：

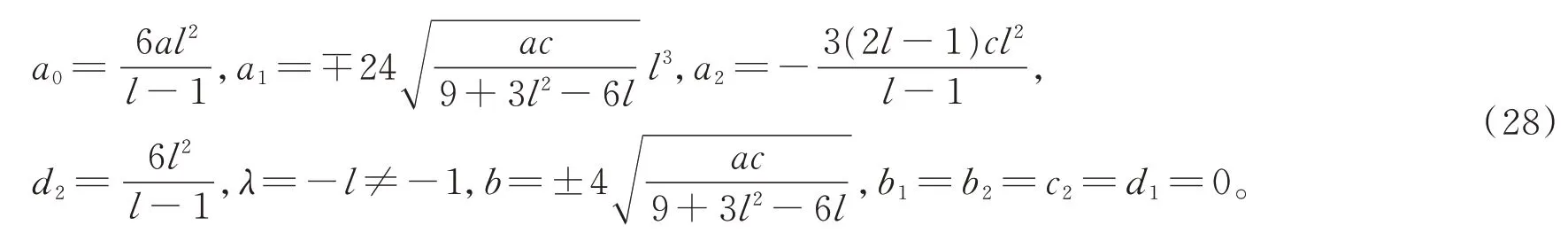
由(10)，（28）的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

情形6：

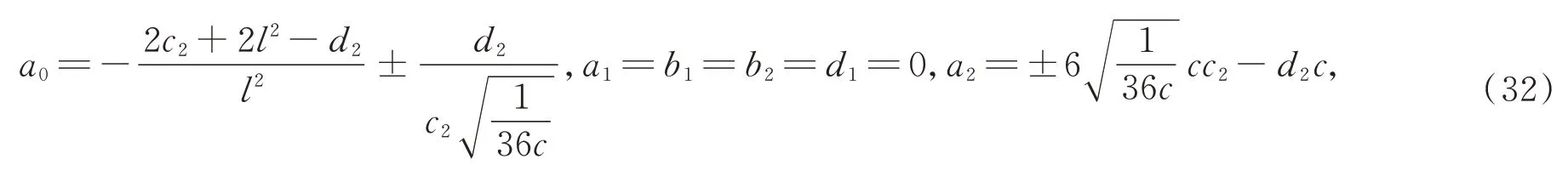
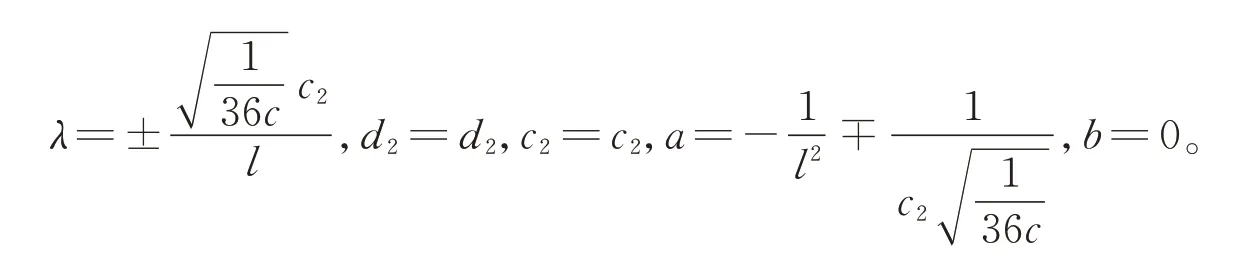
由（10），（32）的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

运用Maple软件得出(35)式解的平面图与三维图(见图4)：-1,c2=-2,d2=2,λ=-,θ=,p=2,η=-2

图4 其中取ε=8,l=1,c=2,a=

情形7：

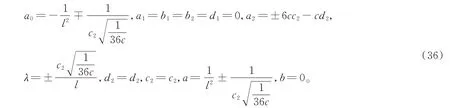
由（10），（36）的解代入假设(11)中可得方程(3)的孤立波解,又根据分数复变换(2)进而可得方程(1)的孤立波解为

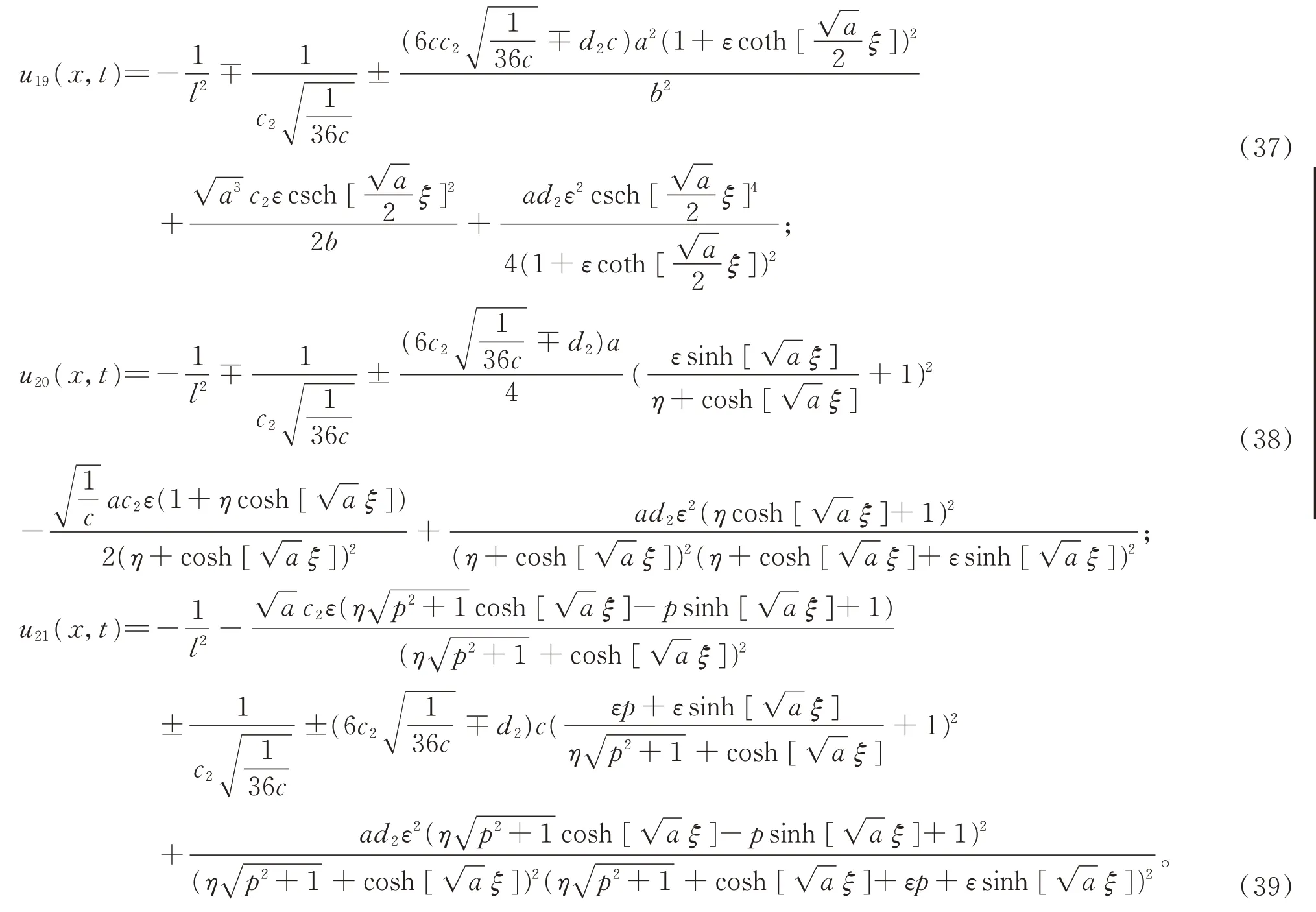
注1：其中的ε,η,p的值是据参考文献[7]中平方项DR方程的对应系数取值。

4 结论

本文通过平面动力系统理论与方法以及改进的辅助方程映射法讨论时间分数阶Burger方程解的存在性及21个有界行波解，所得钟状孤波解都是通过cothξ,sinhξ,coshξ,cschξ形式组合，经查阅文献得知，这种方法得出方程(1)的解的形式是首次得到的，运用此方法扩展了方程(1)的解系；通过对方程(3)进行定性分析，还知有无穷多个周期波解，通过此方法能够求出其部分周期解，已有文献对方程(1)周期波解进行研究，本文没有给出其周期波解。