普粉丽，孙卫新，丁晓敏

1.普洱学院 数学与统计学院，云南 普洱 665000；2.普洱学院 发展规划中心，云南 普洱 665000；3.普洱市思茅区第二小学，云南 普洱 665000

1 研究背景

在互联网快速发展的今天，理解和应用数学已经成为人们日常生活和工作的需求。作为一名非数学专业大学生在将来的社会中分析与解决问题、进行各类计算、使用计算机等都离不开数学。2011 年颁布的《数学课程标准》指出，“数学素养”是现代社会每一个公民应该具备的基本素养[1]。2017 年颁布的《普通高中数学课程标准（2017 年版）》指出，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的[2]。数学素养既是数学教育改革的目标也是提高数学教育质量的关键。

2 数学素养的内涵界定

早在20 世纪80 年代，著名数学教育专家科克罗夫特（Wilfred Cockcroft）就提出“数学素养”是指个人在社会生活中所需要的数学，并能运用数学技能处理日常生活中的数学问题，懂得欣赏和理解用数学语言表达的信息（如图表、曲线、百分比等）[3]。

1994 年张奠宙[4]认为，数学素养包括知识观念、创造能力、思维品质、科学语言。2000 年顾沛[5]认为，数学素养是指抓住数学问题的背景和本质的素养；用准确、严格、简练的数学语言表达数学思想的素养；具有良好的科学态度和创新精神，合理地提出数学猜想、数学概念；探寻解决问题的素养；数学模型的素养。2009 年康世刚[6]认为，学生的数学素养包含数学知识素养、数学应用素养、数学思想方法素养、数学思维素养与数学精神素养。2015 年何小亚[7]认为，数学素养包括数学运算、数学意识、数学推理、数学思想方法和数学情感态度价值观。

3 调查对象

普洱学院地处祖国西南边陲，位于大昆曼国际通道上的枢纽城市——普洱市。40 多年的办学历程，形成了自己的特色。因此，调查对象选取本校的物理教育专业、园林专业、生物教育专业等学生。

4 调查问卷与统计软件

参考杨海艳的《数学专业大学生数学文化素养的调查研究》的问卷，改编本次的调查问卷。问卷设计共20 道目，编号为A1—A7 是对数学的认知考查，编号为B1—B3 是对数学应用意识的考查，编号为C1—C3 是对数学思想方法的考查，编号为D1—D4 是对数学美学价值的考查，编号为E1—E3 是对数学语言与交流的考查。每道题采用5 级量表，从“完全赞同”到“完全反对”分成5 个等级，对应得分从高到低依次记为5 分到1 分，也就是得分越高，说明学生的数学素养越好。共发放问卷169 份，回收且有效问卷为152 份，有效率为95%。本文应用统计软件SPSS24.0 对非数学专业大学生的年级差异进行独立样本T 检验，根据统计结果进行分析。

5 调查结果与分析

5.1 数学知识素养

5.1.1 数学知识素养的调查

问卷调查中显示，91%的学生认同“数学是研究现实世界中一切可能的量的关系的科学”的说法，仅有9%的学生持有反对态度，说明绝大多数学生认同数学是研究现实世界中一切可能的量的关系的科学。数学是大量的公式、定理和枯燥的计算，有30.9%的学生持反对态度，34.2%的学生保持中立态度，34.9%的学生持赞同。这说明学生对数学研究的对象认识还不够明确，部分认识还存在片面性。

对“数学反映了人们积极进取的意志、细致周详的推理、以及对于完美境界的追求”的认识中，仅有10.5%学生持反对态度。“数学问题的答案都是充分的，没有答案的问题不能算数学问题”，有32.2%的学生认为反对，32.2%的学生基本反对，17.1%的学生持中立态度，18.4%的学生赞同。这说明大部分学生都知道数学问题并非都有答案。“数学可以锻炼人们的逻辑思维能力”，有1.3%的学生完全反对，5.9%的学生基本反对，3.9%的学生持中立态度，88.9%的学生赞同。数学是思维的体操，绝大多数学生能认可这种说法，只有少部分学生不赞同。

5.1.2 数学知识素养的年级差异性分析

A1 的p 值为0.966 在于0.05，接受原假设，说明二、三年级的学生对数学是量的关系的科学认识无显著性差异，二、三年级的均值相等。A2 的p 值为0.009 小于0.05，拒绝原假设，说明二、三年级的学生在对数学知识素养有显著性差异，二年级的均值高于三年级的均值。A3 的p 值为0.025 小于0.05，拒绝原假设，说明二、三年级的学生对数学反映了人们积极进取的意志、细致周详的推理、以及对于完美境界的追求有显著性差异，三年级的均值低于二年级的均值。A4 的p 值为0.013 小于0.05，拒绝原假设，说明二、三年级的学生对数学问题的答案都是充分的，没有答案的问题不以能算数学问题的认识存在显著性差异，二年级的均值高于三年级的均值。A5 的p 值为0.232 在于0.05，接受原假设，说明二、三年级的学生对数学可以锻炼人们的逻辑思维能力的认识无显著性差异，三年级的均值高于二年级的均值。A6 的p 值为0.047 小于0.05，拒绝原假设，说明二、三年级的学生对数学的抽象思维能力的认识存在显著性差异，三年级的均值高于二年级的均值。

非数学专业的学生到二、三年级时，有的专业可能会继续学习相关数学课程。这表明二、三年级学生的数学知识素养水平相差不大。

5.2 数学应用意识素养

5.2.1 数学应用意识素养的调查

“数学与人们的社会实践活动密切相关”，2%的学生完全反对，7.2%的学生基本反对，17.8%的学生持中立态度，40.1%的学生基本赞同，32.9%的学生完全赞同。“数学在自然科学和社会科学中都有着广泛的应用”中，3.9%的学生完全反对，3.3%的学生基本反对，13.8%的学生持中立态度，36.1%的学生基本赞同，42.1%的学生完全赞同。“估算、记录、做决定都是数学的应用”，有6.6%的学生反对，27%的学生持中立态度，66.4%的学生持赞同意见。这说明绝大多数学生能正确理解数学应用的特点，只有少数学生对数学应用的认识水平不高。

5.2.2 数学应用意识素养的年级差异性分析

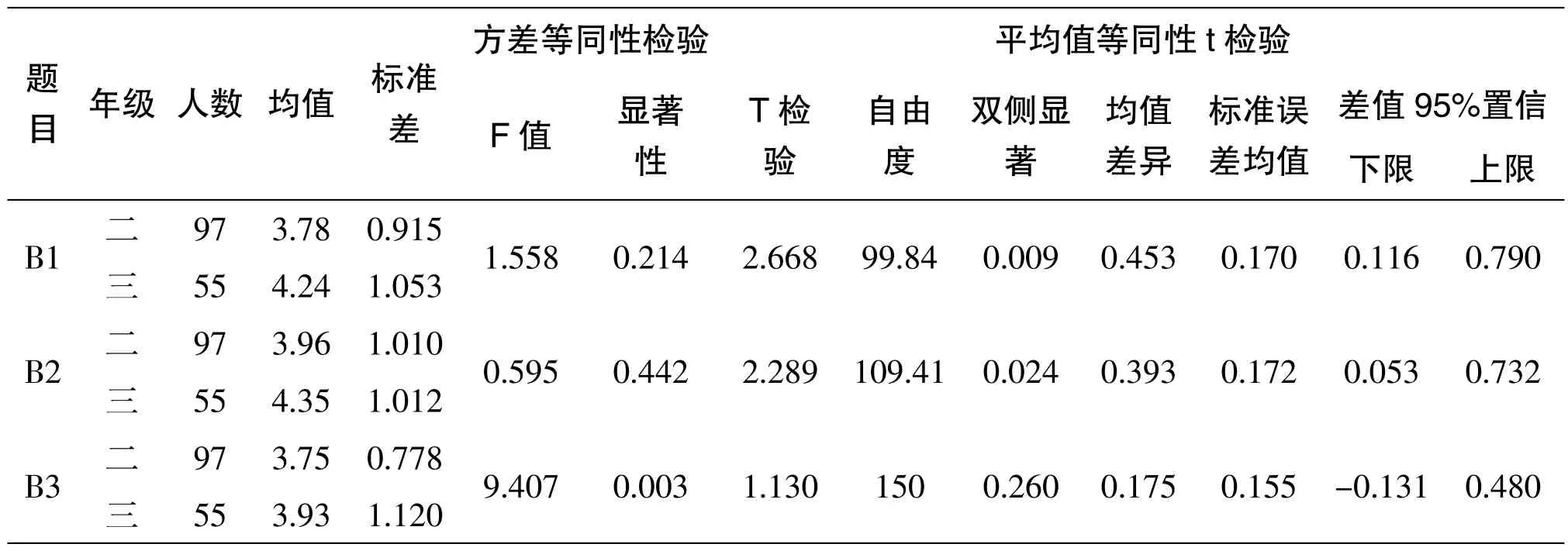
表2 数学应用意识的年级差异

B1 的p 值为0.009 小于0.05，拒绝原假设，说明二、三年级的学生在数学与人们的社会实践活动密切相关的认识中有显著性差异，三年级的均值高于二年级的均值。B2 的p 值为0.024 小于0.05，拒绝原假设，说明二、三年级的学生在数学在自然科学和社会科学中都有着广泛的应用的认识中有显著性差异，三年级的均值高于二年级的均值。B3 的p 值为0.260 大于0.05，接受原假设，说明二、三年级的学生对数学的应用的认识中无显著性差异，但三年级的均值也略高于二年级的均值，说明三年级学生的数学应用意识素养比二年级的学生好。

5.3 数思想方法素养

5.3.1 数学思想方法素养的调查

“数学的发展主要靠严密的演绎推理，与人们的实践活动和归纳法联系不强”中有63.8%的学生反对，有19.7%的学生赞同这一说法。“极限断想是整个数学中最根本最重要的数学思想之一”有仅有8.6%的学生持反对意见；“掌握数学的精神、思想和方法对于一个人在未来工作中解决问题有重要意义”中仅有8.5%的数学持反对态度，66.5%的学生持赞同意见，25%的学生持中立态度，这说明学生对数学精神、思想和方法对一个人未来的生活影响至深。

5.3.2 数学思想方法素养的年级差异性分析

C1 的p 值为0.000 小于0.05，拒绝原假设，说明二、三年级的学生在数学的发展主要靠严密的演绎推理，与人们的实践活动和归纳法联系不强的认识中有显著性差异，三年级的均值小于二年级的均值。C2 的p 值为0.095 大于0.05，接受原假设，说明二、三年级的学生在极限断想是整个数学中最重要的数学思想的认识中无显著性差异，三年级的均值高于二年级的均值。C3 的p 值为0.077 大于0.05，接受原假设，说明二、三年级的学生在掌握数学的精神、思想和方法对于一个人在未来工作中解决问题有重要意义的认识中无显著性差异，但三年级的均值也略高于二年级的均值。

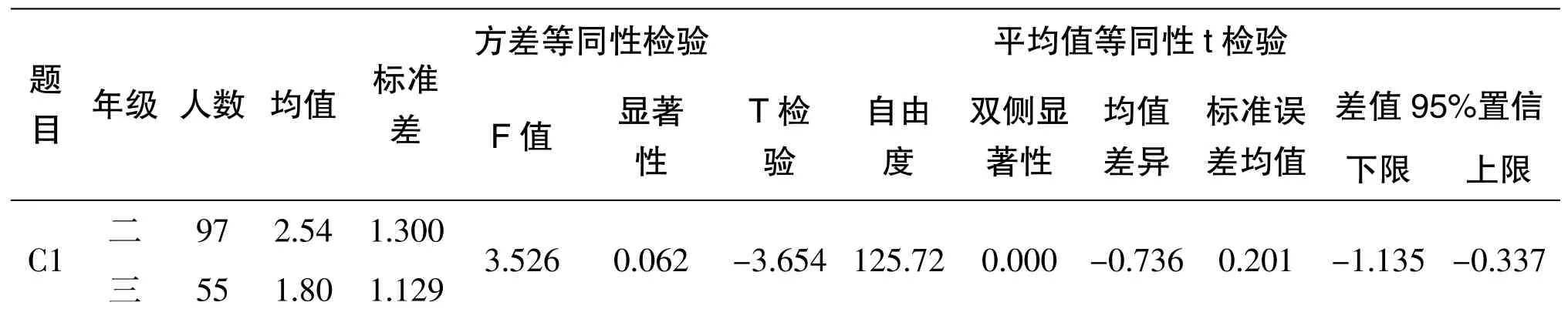
表3 数学的思想方法年级差异

5.4 数学美学素养

5.4.1 数学美学素养的调查

“数学有着和音乐或诗一样的美”有6.6%的学生完全反对，3.9%的学生基本反对，28.9 的学生保持中立，26.3%的学生基本赞同，34.2%的学生赞同。“数学中高度的抽象性、逻辑的严密性和应用的广泛性中也蕴含着极其丰富的审美因素”中仅有2%的学生完全反对，3.9%的学生基本反对，25%的学生持中立态度，30.3%的学生基本赞同，38.8%的学生完全赞同。这表明绝大多数非数学专业的学生除能体会到数学的特点之外也能认识到数学特点之中的美学价值，也有一小部分学生无法体现会数学特点中蕴含的美学价值。“数学具有简单美、对称美、统一美和奇异美”有1.3%的学生完全反对，8.6%的学生基本反对，21.1%的学生持中立态度，32.9%的学生基本赞同，36.2%的学生完全赞同。这说明69.1%的非数学专业学生对数学的美可以从不同的角度审视，数学的简单美、对称美、统一美和奇异美构成数学美的主体。“数学中对复杂的对象施以复杂的运算结果得到最简单的数1，体现了数学是带有神秘色彩的艺术品”有3.3%的学生完全反对，5.9%的学生基本反对，28.3%的学生持中立态度，30.9%的学生基本赞同，31.6%的学生完全赞同。这说明绝大多数学生能感受到数学的简洁美。

5.4.2 数学美学素养的年级差异性分析

D1 的p 值为0.001 小于0.05，拒绝原假设，说明二、三年级的学生在数学中高度的抽象性、逻辑的严密性和应用的广泛性中也蕴含着极其丰富的审美因素的认识中有显著性差异，三年级的均值高于二年级的均值。D2 的p 值为0.000 小于0.05，拒绝原假设，说明二、三年级的学生在数学具有简单美、对称美、统一美和奇异美的认识中有显著性差异，三年级的均值高于二年级的均值。D3 的p 值为0.075 大于0.05，接受原假设，说明二、三年级的学生在数学中对复杂的对象施以复杂的运算结果得到最简单的数1，体现了数学是带有神秘色彩的艺术品的认识中无显著性差异，但三年级的均值也略高于二年级的均值。

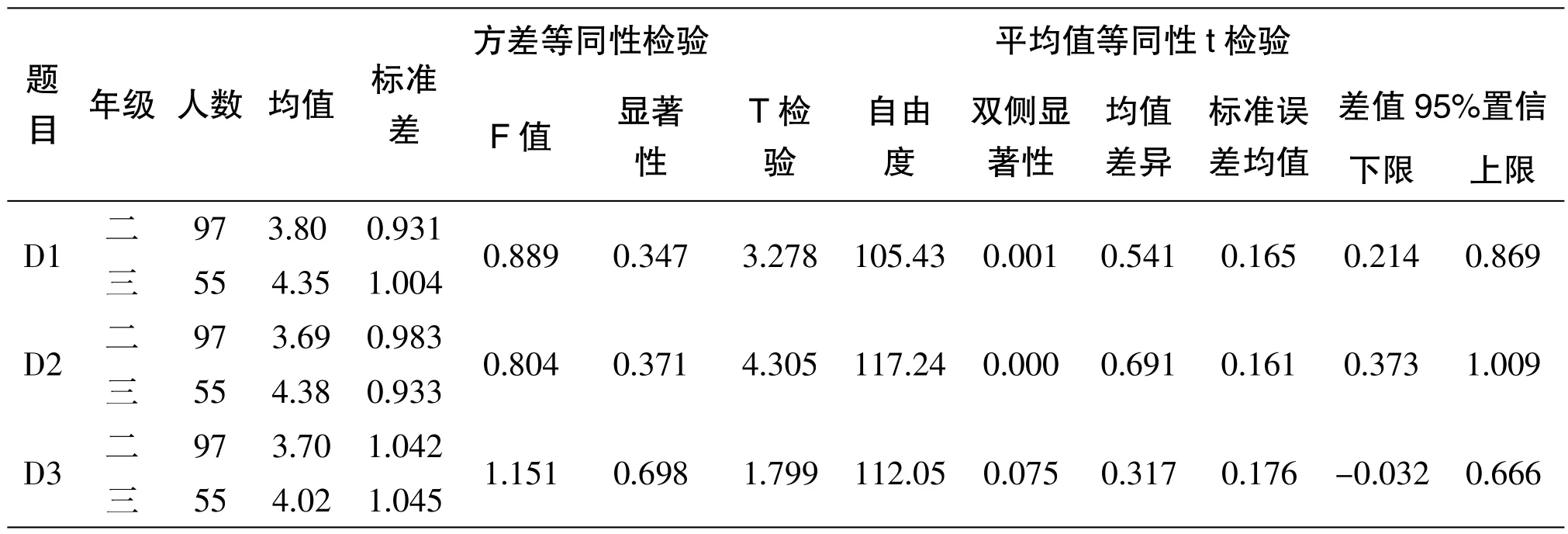
表4 数学美学素养的年级差异

5.5 数学语言与交流素养

5.5.1 数学语言与交流素养的调查

“数学语言是表达和交流的一种重要工具”有3.3%的学生完全反对，12.5%的学生基本反对，25.7%的学生持中立态度，40.8%的学生基本赞同，17.8%的学生完全赞同，将近五分之一的学生并不认同数学语言是表达与交流的一种重要工具。“十进位制计数法是人类最美妙的文明之一”中3.9%的学生反对，34.2%的学生持中立态度，61.9%学生持赞同意见。由此可知，非数学专业学生对数学语言的理解有了一定的认识，但也有少部分学生对数学语言的理解还不够深入。因此，加强数学语言的教学是提升每个人的数学素养途径之一。

5.5.2 数学语言与交流素养年级差异性分析

E1 的p 值为0.045 小于0.05，拒绝原假设，说明二、三年级的学生在数学语言是表达和交流的一种重要工具的认识中有显著性差异，三年级的均值略高于二年级的均值。E2 的p 值为0.004 小于0.05，拒绝原假设，说明二、三年级的学生在数学符号语言对数学的发展有重要的意义的认识中有显著性差异。三年级的均值高于二年级的均值，两个年级的均值都在4 分以上，且三年年级的分数达到4.45 分。E3 的p 值为0.013 小于0.05，拒绝原假设，说明二、三年级学生在十进位制计数法的认识中有显著性差异，三年级的均值高于二年级的均值。

表5 数学语言与交流素养的年级差异性分析

6 提高非数学专业学生数学素养的策略

6.1 注重数学的精神、思想和方法的有效渗透

能否能从数学角度出发，用数学思想方法去分析问题、解决问题，是判断一个人是否具有一定的数学素养。匈牙利著名的数学家罗莎彼德曾有一个生动的比喻：假如在一群科学家面前有煤气灶、水龙头、水壶和火柴，要想烧开水，应当怎么做？这可以锻炼学生处理复杂的实际问题时，自觉地从数学角度出度、用数学的思想方法观察和思考问题，并努力培养学生寻求数学解决问题的办法。

6.2 渗透数学文化知识的教学

能否感知与欣赏美，反映出一个人的素养、情操、品位、境界的高低与否。数学美是数学问题的结论或解决过程适应人类的心理需要而产生的一种满足感。因此，数学有结论之美、方法之美、结构之美，数学之美，美在纯洁，美在和谐，美在对称，美在奇异。因此，教学中融入数学文化知识，培养一定的数学审美情趣，提高审美能力，在美的熏陶下启迪思维，陶冶情操，提升口味，促进学生的数学知识素养与数学美学素养。

6.3 整合数学与其他学科，增强数学应用意识素养

数学是一种工具，一种思维的工具，一种解决数学问题与实际问题的工具。教师教学时，可将社会活动或有社会背景的问题引入到课堂教学时，将有助于发展学生的数学素养。强调学生在理解基本概念的基础上，能应用相关的数学知识来识别、处理和解决这些问题。可加大数学建模和数学在其他学科领域的应用，使学生体会到数学在各行各业的广泛应用意识，激发和培养学生主动运用数学知识的意识与能力，提高大学生的数学素养。

6.4 注重数学语言与交流的教学

数学语言是一切科学的共同语言。比如波动理论靠傅立叶分析来说明，经济学家用数学语言表述经济运行规律；量子力学要通过理论来描述；生物学中的遗传基因DNA 原来是数学中的双螺旋线；物理中的布朗运动成为概率论中的语言；天文学的语言是微积分等。数学课程教学时，鼓励学生学会数学思维、数学表达，从而提升学生的数学素养。

6.5 改变教学方法，增加数学文化素养

“教学有法，教无定法，贵在得法”，在课堂教学中选择合适的教学方法，利用现代教育技术手段与网络教学平台进行教学。借助学习通、学银在线、MOOC 及雨课堂网络教学平台中的数学文化、数学史与数学教育、大学数学等，为学生提供教学视频，方便学生学习，从而增加学生的数学文化素养。