刘艳，冯旭琛，杨睿，黎明，冯一飞

中国海洋大学 工程学院，山东 青岛 266100

0 引 言

自主式水下航行器（AUV）因其灵活性和自主性被广泛应用于海底资源勘探、水下打捞以及海洋测绘等领域[1]。如何快速实现对AUV的精确控制一直是亟待解决的技术难题[2]。通常，AUV控制方法可分为基于模型控制和无模型控制。基于模型控制方法是通过精确揭示AUV所遵循的物理规律和运行机理，在先进的运动控制方法基础上，可以解决风、浪、流扰动下无模型控制方法难以实现的AUV精准控制问题[3-4]。AUV运动学与水动力学模型具有非线性、参数不确定性以及各自由度间的耦合性特点，因此，AUV运动控制系统的设计具有挑战性。

Yang等[5]采用H∞鲁棒控制方法解决了Ciscrea AUV单自由度艏摇模型的非线性和不确定性问题。Rosendo等[6]基于准滑模调节的约束补偿算法和比例微分控制算法，实现了Ciscrea AUV艏摇和垂荡双自由度控制。Guerrero等[7]在AUV六自由度数学模型上设计了去耦合控制器，但前期工作均未考虑耦合参数对控制结果的影响，多自由度耦合控制问题未得到解决。

H∞不确定集合控制方法具有鲁棒性特点，对AUV模型中的不确定性参数不敏感，其控制性能不受扰动和参数变化的影响，可有效解决多自由度耦合控制问题。根据H∞鲁棒控制原理，满足鲁棒稳定性及鲁棒性能要求是设计AUV鲁棒控制系统的两个关键因素。首先，AUV模型中的不确定性参数可表述为不确定集合。根据小增益定理，具有不确定集合作用的闭环系统其鲁棒稳定性等价于标称闭环系统的内部稳定性，且阻尼、附加质量等参数的不确定性分量均可视为不确定集合并予以处理。其次，若AUV模型鲁棒控制器结果满足H∞鲁棒性能要求，则控制器可以保证AUV具有良好的运动控制性能（例如跟踪、干扰抑制和能量最小等），而H∞控制器综合是设计求解H∞鲁棒控制器的关键。

为此，Zames[8]以单输入单输出（single-input single-output，SISO）为对象，提出了基于频域的H∞综合方法，Doyle和Ball等[9-10]面向多输入多输出（multi-input multi-output，MIMO）对象，提出了基于状态空间的DGKF（Doyle-Glover-Khargonekar-Francis）方法。这两种方法都可通过求解代数Riccati方程（ARE)得到H∞综合控制器，但Ciscrea AUV模型存在虚轴附近的极点，采用ARE方法实现H∞控制器综合时，其广义被控对象不满足对应的正则约束条件，而采用基于内点法的线性矩阵不等式(linear matrix inequality, LMI)方法则可完成[11]。不同于ARE方法，LMI方法的正则约束条件较少，可直接求解ARE奇异问题[12]。

基于以上考虑，本文将针对Ciscrea AUV四自由度非线性数学模型的鲁棒控制问题，从耦合控制角度，提出H∞综合控制器设计方法，以实现在外部干扰下的AUV三维轨迹跟踪与艏摇控制。首先，通过摄动法将Ciscrea AUV二次非线性阻尼作用和惯性矩阵的参数不确定性转化为不确定集合，并得到广义系统。然后，针对耦合的广义系统，利用H∞综合方法在稳定的鲁棒控制器上优化闭环系统性能，通过MATLAB软件提供的LMI工具箱[13-14]求解鲁棒控制器。最后，模拟外部干扰下的三维轨迹跟踪和艏摇控制场景。

1 Ciscrea AUV数学模型

本文利用MATLAB完成了Ciscrea AUV数学模型沿螺旋线下沉的仿真。由于仅涉及横荡、纵荡、垂荡和艏摇这4个方向的运动，故只针对Ciscrea AUV四自由度数学模型进行控制仿真。表1所示为Ciscrea AUV数学模型的运动参数。

表1 Ciscrea AUV四自由度数学模型的运动参数Table1 Four-DOF kinematic parameters of Ciscrea AUV

Ciscrea AUV模型的速度向量和位置向量分别表示为V=[u v w r]T和η=[x y zψ]T，已知其水动力模型为

式中：MRB和MA分别为Ciscrea AUV模型的惯性矩阵和附加质量矩阵；D(|V|)为阻尼系数矩阵；g(η)为 回复力；τpro为 推进器输出的推力；τenv为外部干扰力（风、浪、流）。

在不考虑横摇和纵摇自由度的情况下，控制系统可实现AUV运动控制。假设AUV的姿态始终与重力垂直，无需考虑重力与浮力的相互作用，则g(η)可忽略不计。但是，AUV受到的外力包括了推进器输出的推力τpro和 外部干扰力 τenv，其水动力模型又可写为

基于上述AUV模型，考虑质量变化对模型参数的影响。其中，MA仅与AUV的外形有关[15-16]，在实际工程中，AUV搭载的配件（例如相机、机械臂等）对其外形的改变可忽略不计，故MA不受影响。对于形状规则的物体，MA可由经验公式直接计算。然而，Ciscrea AUV是典型的具有复杂外形和开放架构的AUV，经验公式并不适用。因此，文献[17]通过流体计算软件WAMIT计算得到了如下MA，详细计算过程可参见此文献。

Ciscrea AUV模型的惯性矩阵写为：

式中：m为 AUV的自身质量；Izz为AUV绕z轴的转动惯量。

由Solidworks软件可计算得到MRB如下：

鉴于AUV质量变化会影响MRB[18]，故假设MRB具有30%的不确定性，可得到如下含不确定性的惯性矩阵：

H∞综合方法通常适用于线性系统，需要对AUV模型进行线性化。因此，本文采用摄动法[19]将阻尼系数矩阵中的二次非线性作用转换为不确定集合∆d，其中不确定性的变化主要源于AUV作业速度的变化。已知：

式中：Dl为 线性阻尼系数矩阵；Dn(|V|)为非线性阻尼系数矩阵，Dn(|V|)=Dndiag(|V|T)。通过模型辨识实验、STAR-CCM+和ANSYS-CFX这3种方法均可辨识得到四自由度水动力模型的阻尼参数，并取平均值作为最终的参数结果，具体如下[17]：

AUV在整个作业过程中，其速度变化介于初始速度V0与 最大速度Vm之间，其中V0=[0000]T，Vm=[0.50.50.55]T。假设AUV稳定的作业速度为Vm，在该作业速度附近考虑 2 0%的不确定性，则非线性阻尼系数矩阵Dn(|V|)可转化为含不确定性的线性矩阵Dnl，即

式中：Pd=diag(0.2,0.2,0.2,0.2);∆d=diag(δ5,δ6,δ7,δ8)。其中，Pd为 非线性阻尼矩阵的不确定性边界，∆d为非线性阻尼矩阵的不确定集合。

经线性化后，可得到如下具有不确定性的水动力学模型：

式中：M为水动力学模型的惯性矩阵与附加质量矩阵之和；D为水动力学模型的阻尼矩阵。因M和D均为不确定的量，故可使用标称值和不确定集合表述如下：

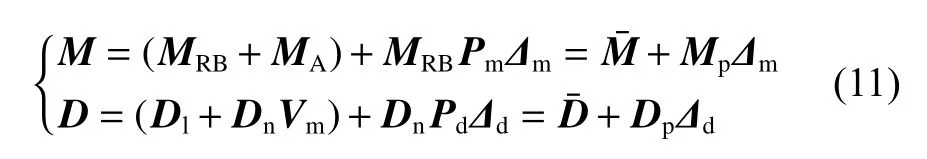
图1所示为不确定性模型的系统结构。其中，系统输入为u，对应AUV所受到的外力，即τpro与τenv之 和；系统输出为y， 对应AUV的位置向量η。如图1所示，不确定性矩阵包含了M−1和D模块。本文采用线性分式变换（LFT）方法[20]将不确定性系统变换为广义系统和不确定集合两个部分。

图1 不确定性模型系统结构图Fig.1 Block diagram of the uncertainty model

其中，模块M−1和D可以表示为上LFT，即

式中：FU为 上LFT的传递函数；Mm为M−1的广义矩阵；Md为D的广义矩阵。

对于广义矩阵P和不确定集合∆组成的上LFT，有FU(P,∆)=P22+P21∆(I−P11∆)−1P12，故可得：

上述各公式可用图2表示，其中um与ym为M−1模块的摄动输入和摄动输出，ud与yd为D的摄动输入和摄动输出，wm与zm为M−1模块的外界输入与输出，wd与zd为D模块的外界输入与输出。

图2 M−1和D的上LFT表示Fig.2 Upper LFT formulation of M−1 andD

综上所述，对于含不确定集合的系统，可以表示为如图3所示的结构，其中，u为 4×1的输入向量，y为 4×1的输出向量。

图3 不确定性系统结构图Fig.3 Block diagram of the uncertainty system

由图3所示不确定性系统结构图，选取状态变量x=[x1x2]T，其中，x1=[xy zψ]T,x2=[uv wr]T，据此，可得到如式（15）所示不确定性系统的状态空间方程。

消去zd，可得：

由Gcis表示CiscreaAUV四自由度广义系统，则Gcis有输入向量[umudu]T和输出向量[ymydy]T，其状态空间可表示为：

其中：

从式(17)和式（18）可以看出，广义系统Gcis不包括不确定性的量，并且Gcis与 不确定集合∆共同组成了Ciscrea AUV不确定性模型。如图4所示，将Ciscrea AUV不确定性模型由上LFT表示为G=FU(Gcis,∆)， 其中 ∆=diag(∆m,∆d) 。Gcis的传递函数矩阵的奇异值曲线如图5所示，图中绘出了Gcis的 4个 奇 异 值 γ1,γ2,γ3,γ4在 频 域 上 分 布 的 曲线。由图可见，开环系统最大奇异值是大于1的，不满足性能约束条件。

图4 开环模型线性分式变换Fig.4 Linear fraction transformation of the open-loop model

图5 广义系统G cis奇异值曲线Fig.5 Singular value curves of the general system Gcis

2 鲁棒控制器综合

图6所示为考虑不确定性系统一般化跟踪问题的原理图。为了方便阐述原理，图中被控对象为单输入单输出系统。其中，r,d,n,e,y,u,yp分别为参考输入、低频干扰、测量噪声、系统误差、控制输入、控制输出和系统测量信号，K为控制器，G为被控对象不确定性模型，它由广义系统P和不确定集合∆组成。将图6表示为图7所示的互连系统。图7中：w为r,d,n组成的外部输入向量，即w=[r d n]T；z′为设计者定义的性能输出向量，包括了e,u,yp； 为了表征期望性能，通常会在z′后串联权重函数矩阵W来评价控制性能，得到评价输出向量z。

图6 一般化的跟踪问题原理图Fig.6 Block diagram of the general tracking problem

图7 H ∞鲁棒综合问题的互连系统表示Fig.7 Interconnection system formulation for robust H∞ synthesis problem

考虑闭环系统鲁棒稳定性，由小增益定理可知：当∆稳 定且 //∆//∞＜1时，不确定的闭环系统鲁棒稳定性等价于标称闭环系统WTw→z′(P,K)的内部稳 定 性，且 //WTw→z′(P,K)//∞＜1成 立。由 下LFT的定义可确定传递函数Tw→z′(P,K)：

此时，无需考虑不确定性扰动对闭环系统鲁棒稳定性的影响，只需考虑标称闭环系统的性能指标。对于控制系统的跟踪问题，通常关注e,u,yp等信号，根据这些信号来衡量闭环系统跟踪能力是否良好、闭环系统响应过程中控制器输出能量是否合理，以及闭环系统是否抑制干扰等。式（21）表示的则是闭环系统的性能输出向量z′=[e u yp]T与外部输入向量w=[rdn]T之间的关系。

通常，采用外部输入信号到特定性能输出信号之间的传递函数的H∞范数来表征性能指标要求，进而通过优化该范数来优化相应的性能指标。表2所示为具体性能指标。

表2 不同性能指标对应的目标函数Table2 Object functions corresponding to different performance indexes

本文针对Ciscrea AUV的MIMO系统干扰抑制问题对闭环系统性能进行了优化，如图8所示。参考输入r和低频干扰输入d组成系统的外部输入向量w， 控制器K、广义系统Gcis和不确定集合∆通过串联反馈形成闭环系统。权重函数矩阵为W=diag(We,Wu,Wp)（其中，下标p表示yp以示简洁），通过将其串联在系统性能输出向量[eu y]T后得到评价性能输出ze,zu,zy组成的向量z=[zezuzy]T，其中权重函数We，Wu和Wp分别用来约束闭环系统对特定信号的跟踪能力、u对外部干扰的抑制能力和y对外部干扰的抑制能力。本文的主要设计目标是抑制外部干扰，系统的性能可以由d到z的H∞范数表示，如式（20）所示。

图8 闭环系统H∞控制框图Fig.8 Block diagram of H ∞ control for the closed-loop system

闭环系统的设计目标是在保证闭环系统的鲁棒稳定性前提下对性能进行优化，因此，对应的H∞鲁棒综合问题可表示为优化问题，如式（21）所示。

根据上文所述不确定系统跟踪问题的鲁棒稳定性条件，可知：当不确定集合 ∆(s)（s表示拉普拉斯变量）稳定且 //∆(s)//∞＜1时，闭环系统的鲁棒稳定性等价于广义系统Gcis与 控制器K互连得到的标称闭环系统的内部稳定性，且 //Td→z(Gcis,K)//∞＜1，亦即

本文在满足闭环系统鲁棒稳定性的前提下，利用经典的ARE方法或LMI方法优化标称闭环系统性能，即求解 min//Td→z(Gcis,K)//∞。为了降低鲁棒控制器的保守性，通常希望优化的目标函数值越小越好。因权重函数是影响优化结果的重要因素，故选取合适的权重函数需要一定的经验[21]。鉴于r,d均为低频信号，闭环系统应在低频的外部输入信号下具有较小的跟踪误差和较强的抗扰性。

因权重函数的逆表征了期望性能，故We,Wp的逆矩阵元素均为高通滤波器。同时，为了最小化控制器的输出能量并统一量纲，本文选取了合适的权重函数，即Wu=diag(0.01,0.01,0.01,0.01)，并且参考Ciscrea AUV艏摇控制器设计方案，经调试得到了如下权重函数：

图9 权重函数逆函数幅频特性曲线Fig.9 Frequency response of the inverse of weighting function

本文利用MATLAB软件中的LMI工具箱求解最优性能函数值，得到一个20维的MIMO鲁棒控制器。图10所示为闭环系统的奇异值曲线，图中绘出了标称闭环系统传递函数//Td→z(Gcis,K)//∞的4个奇异值 γ1,γ2,γ3,γ4在频域上分布的曲线。由图可见，闭环系统的最大奇异值小于1，则//Td→z(Gcis,K)//∞＜1成立，闭环系统的鲁棒稳定性和标称性能满足要求。

图10 闭环系统奇异值曲线Fig.10 Singular value curves of the closed-loop system

3 Ciscrea AUV轨迹跟踪仿真与分析

为了验证所提控制系统的有效性，本文对干扰下的定点跟踪和三维轨迹跟踪进行了仿真，分别给出了参考输入r4×1和 干扰输入d4×1下的标称闭环系统暂态响应，分别如图11和图12所示。

图11 有参考输入下的标称闭环系统暂态响应Fig.11 Transient response of the nominal closed-loop system under reference signal input

图12 有干扰输入下标称闭环系统的暂态响应Fig.12 Transient response of the nominal closed-loop system under disturbance signal input

假设各运动方向的参考输入r(i)和干扰输入d(i)均 为分段的阶跃信号序列，周期为10 s，r(i)=[2.5311.50]，d(i)=[1.5311.50]，i∈{1,2,3,4}。其中，d(i)可简单理解为各运动方向位移（角度）的轻微扰动。图11所示为AUV在横荡、纵荡、垂荡方向的位置x,y,z和 艏摇方向的欧拉角ψ随时间变化的曲线。除了计量单位分别是m和 rad以外，各运动方向的参考输入大小都是一样的。由图可见，输入信号仅含有参考输入r，并随时间变化而变化。系统可以快速（调节时间小于5 s）跟踪参考输入且无超调，从而验证了无外部干扰下闭环系统在x,y,z,ψ方向的跟踪能力。

令参考输入为0，得到图12所示的标称闭环系统在干扰输入下输出信号随时间变化的曲线。由图可见，干扰输入下的系统输出在5s内衰减至0，系统抗扰性得到了验证。

利用MATLAB软件模拟Ciscrea AUV在外部干扰下螺旋下沉的场景。真实的风、浪、流通常以力或力矩形式直接作用在AUV上，并对其产生扰动。本文考虑恒定流速与流向的水流对AUV产生的阻尼力。

假设水流流速vd与水平面的夹角为α，在水平面的投影与AUV纵荡坐标夹角为α1，则水流流速在AUV的x,y,z方向的分量依次为：

水流在固定方向对AUV产生的阻尼力F与流速v的关系表示为

式中：k1,k2分别为二次非线性阻尼系数和线性阻尼系数，各运动方向上的k1,k2值可由阻尼系数矩阵D(|V|)及 水流分量的大小得到。当α=π/6,β=π/3时，通过查表计算，可得流速为 0.3m/s的恒定水流在x,y,z方向产生的水流干扰d=[3.94624.0079 1.8083]TN。

分别在有/无干扰的条件下，令AUV跟踪空间螺旋曲线s1，同时实现1 rad的艏摇角控制：

式中：参考输入s1为 空间螺旋曲线，在 50s时加入水流干扰输入d，在 0∼100s时间段内标称系统的轨迹曲线如图13～图15所示。

图13 有/无干扰下AUV标称系统轨迹跟踪曲线对比Fig.13 Comparison of trajectory tracking curves of the AUV nominal system with and without interference

设AUV初始位置为 (x,y,z)=(0,0,0)，初始艏摇角为 0rad，由图13可见，AUV可以有效跟踪参考轨迹。由图14可见，外界干扰并没有使得系统轨迹严重偏离参考轨迹，系统在干扰下仍然保证了其跟踪精度，这证明了控制系统具有一定的抗扰性。当干扰在ψ方向的分量为0时，由图15可见，x,y,z方向的干扰作用在AUV耦合数学模型上造成了ψ方向的细微扰动，闭环系统在5s内消除了扰动，其有效性得到了验证。

图14 有/无干扰下AUV标称系统轨迹跟踪在不同坐标平面投影曲线Fig.14 Trajectory tracking projection curves of the AUV nominal system on different coordinate planes with and without interference

图15 有/无干扰下AUV艏摇控制暂态响应Fig.15 Transient response of the AUV yawing control with and without interference

为了验证本文所提控制系统的鲁棒性，对不确定性模型G的10个摄动模型进行了闭环系统仿真，结果如图16所示。惯性矩阵MRB以 [0.3;0.2;0.15;0.1;0.05;−0.05;−0.1;−0.15;−0.2;−0.3]的幅度在标称模型上变化，得到了被控对象的10个摄动模型。可以看出，图中的曲线没有明显差别，MRB在有界摄动内变化时不会影响系统控制性能。

图16 有干扰下摄动系统三维轨迹跟踪曲线Fig.16 Three-dimensional trajectory tracking curves of the AUV perturbation system with interference

本文利用小增益定理保证了闭环系统的鲁棒稳定性，在此基础上求解了 min//Tw→z(Gcis,K)//∞，因此求解的控制器K只能满足标称闭环系统的性能条件。本文利用结构奇异值 µ分析方法综合考虑了鲁棒稳定性和鲁棒性能。在范数有界的复数不确定性结构扰动下，分别针对闭环系统鲁棒稳定性和鲁棒性能计算了结构奇异值的边界。

通过下LFT，将标称闭环系统表示为M=FL(Gcis,K)， 其中FL为下LFT，则在该系统上施加范数有界的复数不确定性结构集合∆得到结构奇异值 µ分析框图，如图17所示。图中，w1与w2均为外部输入信号，e1与e2为M模块的输入和输出，M对应于不确定性结构∆的奇异值定义为

图17 闭环系统鲁棒稳定性分析框图Fig.17 Robust stability analysis of the feedback system

图18（a）给出了 µ∆(M11jω ）的上、下界及满足系统鲁棒稳定性的 //∆//∞的上界，经计算可得γ1=0.24373， 当// ∆//∞＜1/0.24373时，不确定的闭环系统均能保持稳定性。图18（b）给出了µ∆(M(jω))的上、下边界及满足系统标称性能的结构奇异值µ，其最大值为0.988 02，而鲁棒性能要求下的1 /γ2最高可达1.114 4，即γ2＜1。 对于本文的∆=diag(∆m,∆d)结构，仅当 //∆//∞＜1/1.1144时，才能满足闭环系统的鲁棒性能。综合以上结果，发现在任意复数不确定性结构满足 //∆//∞＜1/1.1144时，闭环控制系统可保证鲁棒稳定性并满足鲁棒性能要求。

图18 闭环系统结构奇异值方法分析Fig.18 Structure singular value analysis of the closed-loop system

4 结 语

本文针对Ciscrea AUV四自由度的非线性不确定性模型设计H∞鲁棒控制器，并分析了海流干扰场景中AUV三维轨迹跟踪性能。结果表明，标称控制系统可以维持一定的跟踪精度和响应速度，可有效消除干扰力对AUV产生的输出扰动，抗扰性能良好。在摄动系统闭环仿真中，AUV未失稳，控制器的鲁棒稳定性得以验证。本文通过结构奇异值分析得到了系统结构奇异值的上、下界，该上、下界保证了控制器的鲁棒性能。

AUV的H∞鲁棒控制器具有一定的抗扰性，本文求解的是一个四自由度的高阶控制器，但因其结构复杂，给实际工程实现带来了一定的困难。如何求解结构简洁的MIMO鲁棒控制器是未来需要解决的问题。