Xiao-Yu Shen(沈小宇) Shuai Su(宿帅) and Hai-Liang Hou(侯海良)

1School of Automation,Central South University,Changsha 410083,China

2National Engineering Research Center of Rail Transportation Operation and Control System,Beijing Jiaotong University,Beijing 100044,China

3State Key Laboratory of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China

Keywords: multiagent systems,nonconvex input constraints,switching topologies,distributed optimization

1. Introduction

The distributed optimization problem of multiagent systems has already been one of the most popular problems in the field of control.[1–26]The aim of distributed optimization is to minimize the global objective function in a distributed manner,where the global objective function is the sum of the local objective functions of all agents. Primary studies about distributed optimization mostly focused on the unconstrained case. For example, in Refs. [1–4], distributed optimization problems with the convex or strongly convex objective functions with locally or globally Lipschitz gradients were considered for optimal distribution convergence. Recent studies about distributed optimization paid more and more attention to the constrained case. For example, in Refs. [5–8], distributed discrete-time and continuous-time optimization problems with convex position-state constraints were investigated,

where the gradient stepsizes all are uniform, and those in Refs.[7,8]are diminishing. Also,in Refs.[9–11],distributed optimization problems with inequality constraints, positivity constraints and coupled-constraints were studied. The constraints in the these existing works were usually assumed to be convex. In reality, the agent systems are often subject to nonconvex constraints rather than convex constraints. For example,the quadrotors can move in every direction but the region formed by the driving forces is nonconvex. To deal with the nonconvex constraints, some works have been performed in Ref.[12].However,the results in Ref.[12]were on the consensus problem and the optimization problem was not considered.In Ref.[13],while distributed optimization with nonconvex constraints was studied, the nonconvex constraints were only on the velocities of the agents.

Inspired by Refs. [12,13], in this paper, we address the distributed optimization problem of discrete-time multiagent systems with nonconvex control input constraints, switching topologies and nonuniform stepsizes, where local objective functions are general differentiable and convex. We first introduce a novel distributed optimization algorithm with a switching mechanism to guarantee that all agents eventually converge to an optimal solution point, while their control inputs are constrained in their own nonconvex region.It is worth noting that the mechanism is performed to tackle the coexistence of the nonconvex constraint operator and the optimization gradient term. Based on the dynamic transformation technique,the original nonlinear dynamic system was transformed into an equivalent one with a nonlinear error term. By utilizing the nonnegative matrix theory, it is shown that the optimization problem can be solved when the union of switching communication graphs is jointly strongly connected.

In contrast to Ref. [13], where the nonlinearities are caused by the position constraints,the velocity constraints and the local objective functions, in this paper the nonlinearities are caused by the input constraints and the local objective functions. As is well known,there are no general rules to determine whether a certain nonlinear system is stable, and any small difference might lead to completely different dynamics. Moreover,different from most of the existing works,e.g.,Refs. [1–5,9], nonuniform stepsizes were taken into account,which together with nonconvex input constraints destroy the balance of the optimal convergence of the objective functions.Hence,all the existing approaches based on the graph balance cannot be applied in this paper.

Notation: Rrrepresents the real column vectors set withrdimensions;Rr×nrepresents the real matrices set withr×ndimensions;Irrepresents the unit matrix withrdimensions;xTrepresents the transpose of the vectorx;||x||represents the standard Euclidean norm of the vectorx;PH(h)represents the projection of the vectorhon the closed convex setH, i.e.,PH(h)=argmin¯h∈H‖h−¯h‖;∇f(x)represents the gradient of the functionf(x) atx; the symbol / represents the division sign;⎿A」ijrepresents theijth entry of matrixA; and 1 represents a column vector whose dimension is compatible and elements all are one.

2. Preliminaries

LetH(N,V) represent a directed graph, whereN={1,...,n}denotes the set of nodes, andV ⊆N×Nrepresents the set of edges. The edge(j,i)∈Vmeans that agentjcan transmit information to agenti. We useai jto denote the weight of edge (j,i),aij ≥¯µif (j,i)∈V, andaij=0 otherwise,where ¯µis a positive constant. LetNi={j ∈N:(j,i)∈V}be the set of neighbors of agentiandLdenote the Laplacian of the directed graphH. A sequence of ordered edges(i1,i2),(i2,i3),...represents a directed path. A graphHis strongly connected if there exists a directed path from every node to every other nodes.

A matrixG=[gi j]∈Rr×nis a stochastic matrix if all elements ofGare nonnegative and each row sum ofGis 1,i.e.,gij ≥0 andG1=1.

3. Model and problem statement

The multi-agent system under consideration consists ofnfirst-order discrete-time agents. LetH(kT)represent the communication graph of the system at timekT, whereTis the sampling time and each agent is regarded as a node inH(kT).When no confusion arises,we use(k)instead of(kT)for simplicity of expression throughout this paper.

Suppose that the dynamics of each agent is

wherexi(k)∈Rrrepresents the position state of agenti,ui(k)∈Rrrepresents the control input,and SUi(·)denotes the constraint operator of control input of agentisuch that

It should be noted that the operator SUican be used to describe the nonconvex constraints while the existing convex operators including the saturation operator and the projection operator can only be used to describe the hyperplane constraints or the convex constraints. In practical applications, the systems are often subject to nonconvex constraints.

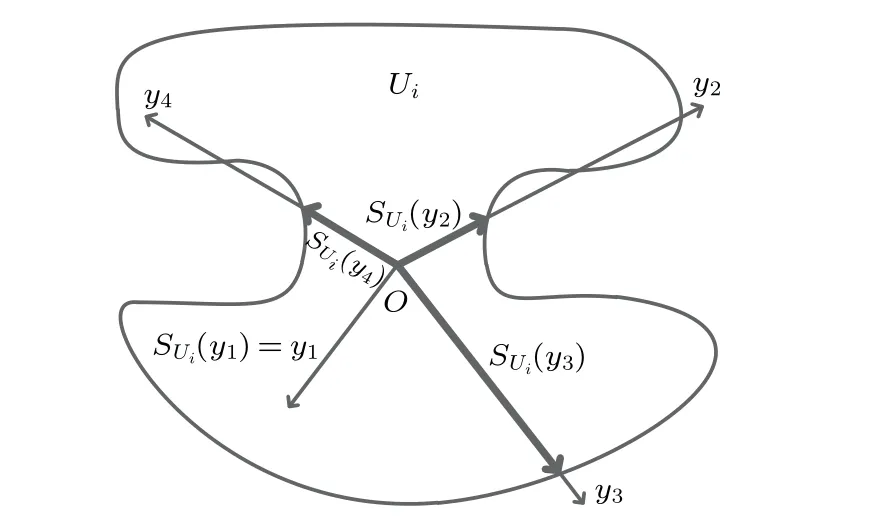
Fig.1. Some examples of the constraint operator.

wherefi(x):Rr →R represents the local objective function of agentiand is only known by agenti. Letfi(x) be convex and differentiable. Hence,∑ni=1fi(x)is a convex differentiable function.

For the following analysis, we useXi≜{x|∇fi(x)=0}andX≜{x|∑ni=1∇fi(x)=0}to represent the optimal set of the local objective functionsfi(x) and the optimal set of the global objective function ∑ni=1fi(x) respectively. Then, we make the following assumption.

Assumption 2[14]Suppose that each setXiis nonempty and bounded for alli ∈N.

4. Main results

4.1. Algorithm and model transformations

(1)Algorithm

To solve the optimization problem, the proposed distributed control algorithm for each agent has the form given by

In the following analysis, we only discuss the case ofr=1 for simplicity of expression,and the general case ofr>1 can be analyzed in a similar way.

(2)Model transformations

Due to the coexistence of nonconvex control input constraints and nonuniform gradient stepsizes, it is very hard to analyze the system stability directly. To tackle this problem,we first make model transformations for system(1)with Eq.(3)so as to fully explore the convexity of the closed-loop system.

for allk. Under Assumption 1, it is clear that ˜pi(k)=1 ifui(k)=0 or SUi(ui(k))=ui(k),0< ˜pi(k)<1 ifui(k)/=0 and SUi(ui(k))

Then, the system (1) with Eq. (3) can be converted into the following equivalent system:

4.2. Main theorem

Before giving the main theorem,the following necessary assumptions and lemmas are first introduced:

Assumption 3[13]Suppose that there exists a positive constantρsuch that 1>ρ> ∑j∈Ni(k)ai j(k)Tfor alliandk ≥0.

Remark 2 The role of Assumption 3 is to ensure the system matrix to be nonnegative. The role of Assumption 4 is to ensure the persistence of the information flow between agents.In Assumption 4, the union of the graphs is only required to be strongly connected everyαtime and the graph at each time might not be strongly connected. The role of Assumption 5 is to ensure the balance of the optimal convergence of all agents.

Lemma 1[27]Letf0(x):Rr →R be a differentiable convex function.Then,f0(x)is minimized if and only if ∇f0(x)=0.

It is easy to see that for alli,Mi(kl+6ni)≤12n(α+1)ε1/βifMi(kl)≤12n(α+1)ε1/βholds. In addition, ifMi(kl)>18n(α+1)ε1/β, thenMi(kl+6n)−Mi(kl)<−12n(α+1)ε1.Therefore, it follows that there must exist a constantT1>T0such thatMi(kl+6n j)≤18n(α+1)ε1/βfor allkl+6n j>T1. In view of the arbitrariness of the constantsklandε1,lettingkl →+∞andε1→0,it follows that limkl→+∞[ψi(kl)−ψj(kl)]=0 for alli,j. Recall that‖ψ(k+1)−ψ(kl)‖≤‖Ξ(k,kl)ψ(kl)−

whereσ ∈X.This implies that all agents will eventually reach a common point in the optimal set of the objective function(2).

Remark 3 The advantages of our results are mainly in three aspects. First, in our algorithm, nonuniform stepsizes are considered. In most of the existing works, the stepsizes were usually assumed to be uniform at any time. In Ref.[17],nonuniform stepsizes are considered, whereas the stepsizes are given in the form of square root which is a special case of ours. Second, the communication graphs considered are jointly strongly connected. Only a few of existing works have considered such switching graphs. Third, nonconvex input constraints are considered in this paper. In Ref. [13], nonconvex constraints have been considered, but the nonconvex constraints are on the velocity state rather than the input constraints.

5. Simulation example

Figures 3 and 4 show the simulation results for the system(1)using algorithms(3).It is clear that all agents cooperatively reach a consensus point in the optimal set and all control inputs are in the bounded nonconvex set, which is consistent with Theorem 1. Another objective of Figs.5 and 6 is to compare the convergence rates of the algorithm when the parametermis adopted as different values. From the simulations, it can be observed that the convergence rate of the algorithm whenm=5 is faster than the case ofm=2. Also,we consider the impact of the initial values on the convergence rate in Figs.6 and 7. From the simulations,it can be observed that the convergence rate is sensitive to the initial values of the stepsizes.

Fig.2. A group of directed graphs.

Fig.3. The position trajectories of all agents.

Fig.4. The control inputs with nonconvex constraints of all agents.

Fig.5. The optimal convergence of agents when m=2 and the initial value of the stepsizes is 0.1.

Fig.6. The optimal convergence of agents when m=5 and the initial value of the stepsizes is 0.1.

Fig.7. The optimal convergence of agents when m=5 and the initial value of the stepsizes is 10.

6. Conclusion

We have solved a distributed optimization problem of the first-order discrete-time multi-agent systems with nonconvex control input constraints,nonuniform stepsizes and switching topologies. The proposed distributed algorithms ensure that all agents cooperatively reach a consensus point in the optimal set and all the agents’inputs are constrained in their own nonconvex region. A switching mechanism was introduced to tackle the coexistence of the nonconvex constraint operator and the nonuniform gradient term. It is proved that the constrained distributed optimization problem can be solved when the union of the switching communication graphs is balanced and jointly strongly connected.