Li Sun,Jierong Liang

1 College of Mechanical and Electrical Engineering,Hohai University,Changzhou 213022,China

2 Department of Chemical and Biochemical Engineering,Technical University of Denmark,2800 Kgs.Lyngby,Denmark

3 Department of Energy Conversion and Storage,Technical University of Denmark,2800 Kgs.Lyngby,Denmark

Keywords:Thermodynamic modeling Liquid density Activity coefficients of individual ions Gas solubility

ABSTRACT An electrolyte Equation of State is presented by combining the Cubic Plus Association Equation of State,Mean Spherical Approximation and the Born equation.This new model uses experimental relative static permittivity,intend to predict well the activity coefficients of individual ions(ACI)and liquid densities of aqueous solutions.This new model is applied to model water+NaCl binary system and water+gas +NaCl ternary systems.The cation/anion-water interaction parameters of are obtained by fitting the experimental data of ACI,mean ionic activity coefficients (MIAC) and liquid densities of water+NaCl binary system.The cation/anion-gas interaction parameters are obtained by fitting the experimental data of gas solubilities in aqueous NaCl solutions.The modeling results show that this new model can correlate well with the phase equilibrium and volumetric properties.Without gas,predictions for ACI,MIAC,and liquid densities present relative average deviations of 1.3%,3.6%and 1.4%compared to experimental reference values.For most gas-containing systems,predictions for gas solubilities present relative average deviations lower than 7.0%.Further,the contributions of ACI,and salting effects of NaCl on gases are analyzed and discussed.

1.Introduction

Aqueous electrolyte solutions,especially sodium chloride(NaCl) systems widely exist in geological fluids,seawater and chemical productions.Due to the complexity and wide industrial application of the aqueous electrolyte solutions,both experimental and theoretical studies have attracted considerable interest.Phase equilibrium and volumetric properties are equally crucial for the geochemistry,petroleum,and chemical industries.And the activity coefficients of individual ions (ACI) have attracted much attention because they are essential for biological systems,membrane processes [1].

Thermodynamic models can mathematically describe the phase behavior of electrolyte solutions.Compared with the so-called fugacity-activity approach,the so-called fugacity-fugacity approach (i.e.electrolyte Equation of State,e-EoS) provides a consistent thermodynamic framework for aqueous electrolyte solutions.Several e-EoS have been presented for modeling aqueous electrolyte solutions.Zuo and Guo[2]pretended an electrolyte version of Patel-Teja EoS by adding a Debye-Hückel term [3].Harvey and Prausnitz [4] developed an e-EoS,which based on a shortrange perturbed term with Lennard-Jones potential,Mean-Spherical-Approximation (MSA) term [5],and Born equation [6].Aasberg-Petersen et al.[7] pretended an e-EoS by combining four-parameter ALS EoS and modified Debye-Hückel electrostatic contribution.Søreide and Whitson [8] developed an e-EoS by extending the Peng-Robinson EoS.Some e-EoS were developed based on statistical associating fluid theory (SAFT).Based on the SAFT for potentials of variable range to electrolytes,Schreckenberg et al.[9] developed an e-EoS by adding a Born equation.Sun and Dubessy [10] improved and extended Lennard-Jones SAFT by adding an MSA term.Tan et al.[11] presented an e-EoS by coupling perturbed-chain SAFT with primitive MSA term.Rozmus et al.[12] extended PPC-SAFT by adding an MSA term and a Born term.

The Cubic Plus Association EoS (CPA) [13] was developed for describing associating fluids(e.g.fluid water,H2O),which contains hydrogen-bonding.So,some e-EoS have been presented based on CPA for aqueous electrolyte solutions.Tan et al.[11] developed a model that combined CPA,primitive MSA term and Born equation.Haghighi et al.[14] combined CPA and a modified Debye-Hückel electrostatic term.Maribo-Mogensen et al.[15]developed an electrolyte version of CPA by adding Debye-Hückel electrostatic contribution,and Born equation.Courtial et al.[16] presented an e-EoS based on CPA,by adding MSA term and Born term.

Most of the above e-EoS perform satisfactorily for phase equilibrium at low salt molalities.At high salt molalities,some models[4,7,8,11]show poor predictive abilities.Some models[2]can only be applied over narrow temperature-pressure ranges.Using e-EoS for the liquid phase allows calculating the liquid densities.Unfortunately,limited models[10,11,16]show good predictions of volumetric properties.Several modeling investigations have been presented for ACI;however,no e-EoS can predict well the ACI.

In this work,we present a new model representing simultaneously phase equilibrium and volumetric properties.Based on the CPA EoS,this new model uses MSA term and Born term to consider the electrostatic interactions.The two most essential innovation points of this model are accurately predicting the ACI and liquid densities.

This manuscript is divided into three main parts:Section 2,the e-EoS is detailed with a description of the contributions to the total Helmholtz free energy.Section 3,the parameter estimation and the modeling results are presented in each case.Section 4,the main conclusion.

2.Thermodynamic Model

2.1.Literature studies of the II+IW theory

Understanding the ACI is a basis for understanding the whole aqueous electrolyte systems.Investigation of ACI and analysis of the terms of electrolyte models may provide insight into the models’ capabilities and contributes to the development of improved models for electrolyte solutions.

Some measurement works for ACI have been published.Based on classical thermodynamic theories of electrolyte solutions (i.e.Debye-Hückel theory [3]),some modeling works [17] have been presented to model the ACI in aqueous solutions.Valiskó et al.[17]presented the“II+IW”theory in which they divide the excess chemical potential into the ion-ion interaction part and ion-water interaction part,respectively.Shilov and Lyashchenko [18]extended the original Debye-Hückel theory[3],they also presented ion-ion contribution and ion-water ion-ion contribution of excess chemical potential.Shilov and Lyashchenko[18]named this model“EDH”(extended version of Debye-Hückel).The“EDH”can be considered as a version of“II+IW”theory.In Shilov and Lyashchenko’s work [18] and Valiskó et al.’s works [17],qualitative agreements with experimental data are obtained.

“EDH” and “II+IW” both suggest that the activity coefficient depends on the balance between ion-ion and ion-water interactions;they both use the Born equation to consider ion-water interaction.In “II+IW”,Monte Carlo simulation and MSA are recommended for ion-ion interaction calculation.In “EDH”,the ion-ion interaction calculation is based on Debye-Hückel theory.Debye-Hückel and MSA do not consider ion association,while Monte Carlo simulation includes ion association calculation.

There is no adjustable parameter in“II+IW”and“EDH”models,and in the“EDH”[18]and“II+IW”[17]calculations,experimental volumetric properties and relative static permittivity (εr,concentration-dependent) are used [19].

In “EDH”,the sum of cation and anion radii are treat as the Debye-Hückel distance of closest approach.In the ion-water calculation of“EDH”,the average value of cation and anion radii is used.“II+IW” uses individual ion radius in both ion-ion and ion-water interaction calculations.Moreover,“II+IW”uses the different type of radii in the two terms(the Born radius is obtained from regression of hydration Gibbs energies).

Although the “II+IW” theory is simplified,it can represent the fundamental interactions present in electrolyte solutions[20].The“II+IW” theory does not contain any “physical forces” terms;it cannot describe a wide range of properties for aqueous electrolyte solutions.Adding physical contributions to activity coefficients,and combining the“II+IW” theory and EoS should be considered,our model combines the “II+IW” theory and physical contributions (EoS) to build a new thermodynamic model.

2.2.Thermodynamic model

The CPA EoS [13] contains a Soave Redlich Kwong term for the physical interactions and an association term especially describing associating fluids (e.g.liquid H2O).So,the e-EoS based on CPA is very appropriate for aqueous electrolyte solutions.The longrange electrostatic forces between charged molecules should be taken into account for mixtures containing electrolytes[21].In this work,we apply MSA term [22] for the ion-ion interaction calculations and Born equation [6] for the ion-water interaction calculations.

The residual Helmholtz energy in this model is given by:

ASRKand AAssocare the residual Helmholtz energy from physical part and the association part,respectively,the details can be found in the original paper[13].AMSAand ABornare the residual Helmholtz energy from the MSA term[22]and Born equation[6],respectively.

It needs to point out that there is no association contribution from ions,so the only no-electrolyte part has an association term.

In this model,the MSA term and Born term are used to calculate the electrostatic interactions.MSA uses a more “modern” method of computing the excess Helmholtz energy from the electrostatic interactions than Debye-Hückel theory [3].

The MSA expression for the excess Helmholtz energy is according to Harvey et al.[23],by using an average diameter σ of the ions,the expression is reduced to a simpler,explicit form [23]:

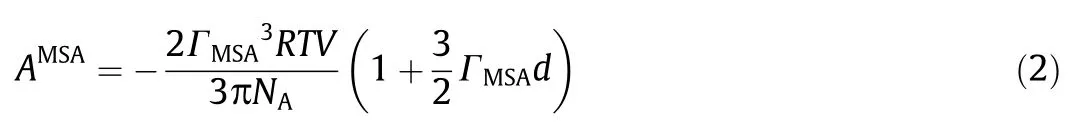
The average diameter d is calculated using the diameter of ions

ΓMSAis given with an implicit expression:

The expression of inverse Debye length (κ) is:

Here,V is total volume,NAis the Avogadro constant,niis the number of mole of ion i,and Ziis the charge of ion i.

The excess Helmholtz energy from ion-water interaction is calculated using the Born equation [6]:

where rBorn，iis Born radius of ion i,and e is the elementary charge.

The Huron-Vidal/NRTL infinite pressure mixing rule offers additional flexibility that let the EoS accurately correlate binary interactions in complex electrolyte mixtures.

In this model,for the binary system involving an ion:

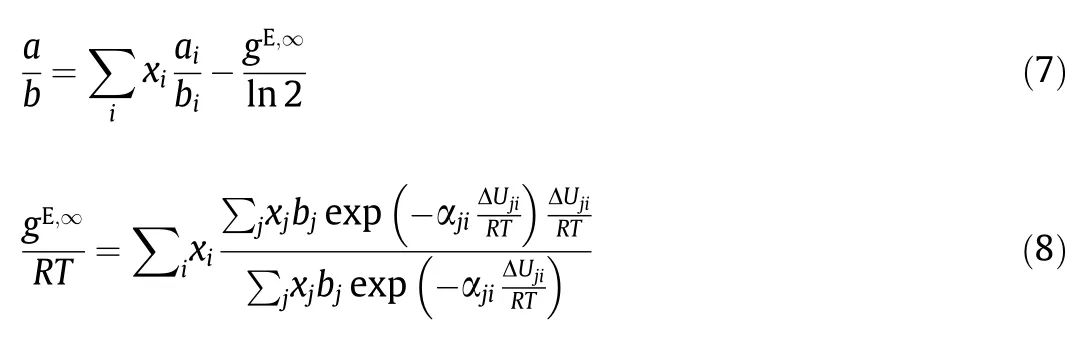
where gE，∞is the excess Gibbs energy at infinite pressure calculated with the NRTL equation,αjiis the NRTL non-randomness parameter,ΔUjiis the change in interaction energy between like and unlike interactions (ΔUji=ΔUij-ΔUjj).

In order to apply this e-EoS over wide temperature ranges,a quadratic temperature dependency for the interaction parameter was presented:

Courtial et al.[16]use the MSA expression,which is more complicated than that used in this work.Courtial et al.[16] used the classical van der Waals one fluid mixing rules for a binary system involving an ion.In contrast,this work uses Huron-Vidal/NRTL infinite pressure mixing rule for a binary system involving an ion.From these two aspects,we can say that our model offers greater flexibility and simplicity.

2.3.Parameter estimation

In order to simplify this model,several assumptions are made:the temperature-dependent parameter,CPA reduced energy parameter (Γi,Γ=a0/(Rb)) of ions are set to zero;the ions are assumed to be non-associating,thus eliminating the two association parameters.The NRTL non-randomness factor (αji) and the ion-ion interaction parameters are set to zero.Then,the three size parameters di,rBorn，iand biare connected with only ion-water/gas interaction parameters left.

Moreover,the ion-solvent and ion-gas interaction parameters are converted to cation/anion-solvent parametersCation/anion-gas interaction parameterswhich means that interaction parameters between cation and solvent are equal to those between anion and solvent,interaction parameters between cation and gas are equal to those between anion and gas.

The “II+IW” theory investigations [17,19] concluded that the ion size,liquid density are essential for electrostatic interaction calculations,and the εrshould be the experimental values in electrostatic interaction calculations [17,19].

Other electrolyte versions of CPA use different approaches of εr.Maribo-Mogensen et al.[15]introduce a new model for the εrcalculation,eliminating the kinetic depolarization effects.However,the theory of kinetic depolarization is controversial.In Courtial et al.’s work[16],the expression is related to temperature and liquid density.Our model presents an experimental expression of the εr,which relates to electrolyte molality and temperature.For aqueous NaCl solutions,the expression is:

Fig.1 shows the correlation results for the εrof aqueous NaCl solutions.From the results,we can see that using Eq.(10) gives good agreements with experimental data over wide temperaturemolality ranges for aqueous NaCl solutions (e.g.relative average deviation are 4.5%,3.2%,3.1% and 5.3% for 273.15 K,298.15 K,313.15 K and 333.15 K respectively).It should be noticed that,rare experimental data of relative static permittivity for aqueous NaCl solution have been published over wide temperature-molality ranges.Furthermore,the published values are different between different measurements.

In Maribo-Mogensen et al.’s calculations [15],the hydrated ion radii from Marcus are used in ion-ion interaction calculation,Born radii (obtained by fitting the experimental data of free hydration energy) are used in ion-water interaction calculations.In Courtial et al.’s calculations [16],the ion radii (0.80 × 10-10m and 2.15 × 10-10m for Na+and Cl-,respectively) used in calculations are neither the Pauling radii [25] nor the hydrated ion radii from Marcus,and the values are far from Pauling radii [25](0.95×10-10m and 1.81×10-10m for Na+and Cl-,respectively).Courtial et al.[16]used the same ion radii in both ion-ion and ionwater interaction calculations.

The“II +IW” theory[17,19]investigations show that the physical ion size (i.e.Pauling radius) [25] should be used in ion-ion interaction calculations,the Born radii should be used in ionwater interaction calculations.

The Born radius is defined from the hydration free energy of the ion,but not all ions have experimental data of free hydration energy.In order to improve the model applicability,the Born radius can be estimated by using the “L-P-S” equation [26] (has been supported by molecular simulation).

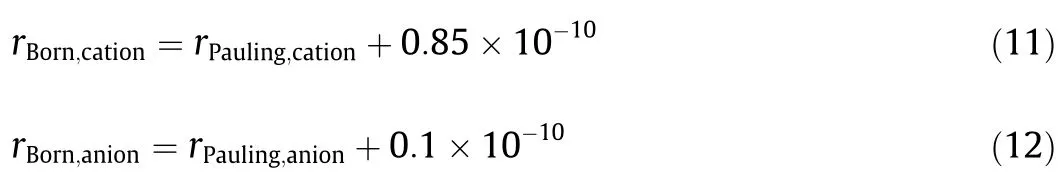
Volumetric properties are critical for both non-electrolyte and electrolyte calculations.An ion has a volume;the volumeexclusion from ions should be considered [21].

In Maribo-Mogensen et al.’s[15]and Courtial et al.’s[16]calculations,the CPA co-volume parameter of an ion is predicted using the following equation [21]:

rion-ion，iis the crystallographic ion radius of ion i used in ion-ion interaction calculations.

However,the calculated CPA co-volume parameter of ion(using Eq.(13)) may underestimate the liquid densities of aqueous electrolyte solutions.One possible explanation is that their CPA covolume parameters of ions overestimate the volume-exclusion from ions in water.The CPA co-volume parameters of ions,which reflect the right ion volume-exclusion,should be used to correlate the liquid densities accurately.In this work,the CPA co-volume parameters of ions are included in the regression.Moreover,the bcand baare assumed to equal to each other,then one CPA covolume parameter bc/afor Na+and Cl-.

For gas-containing systems,the gas solubilities (i.e.mole fractions of gases in liquid phase) are calculated by a two-phase PTflash with the successive substitution method,and we assume that there is no salt/ion in the vapor phase.The cation/anion-solvent interaction parameters and CPA co-volume parameters of ions are obtained from the regression of the ACI,mean ionic activity coefficients (MIAC) and liquid densities of aqueous electrolyte solutions.The cation/anion-gas interaction parameters are obtained from the regression of gas solubilities in aqueous electrolyte solutions.

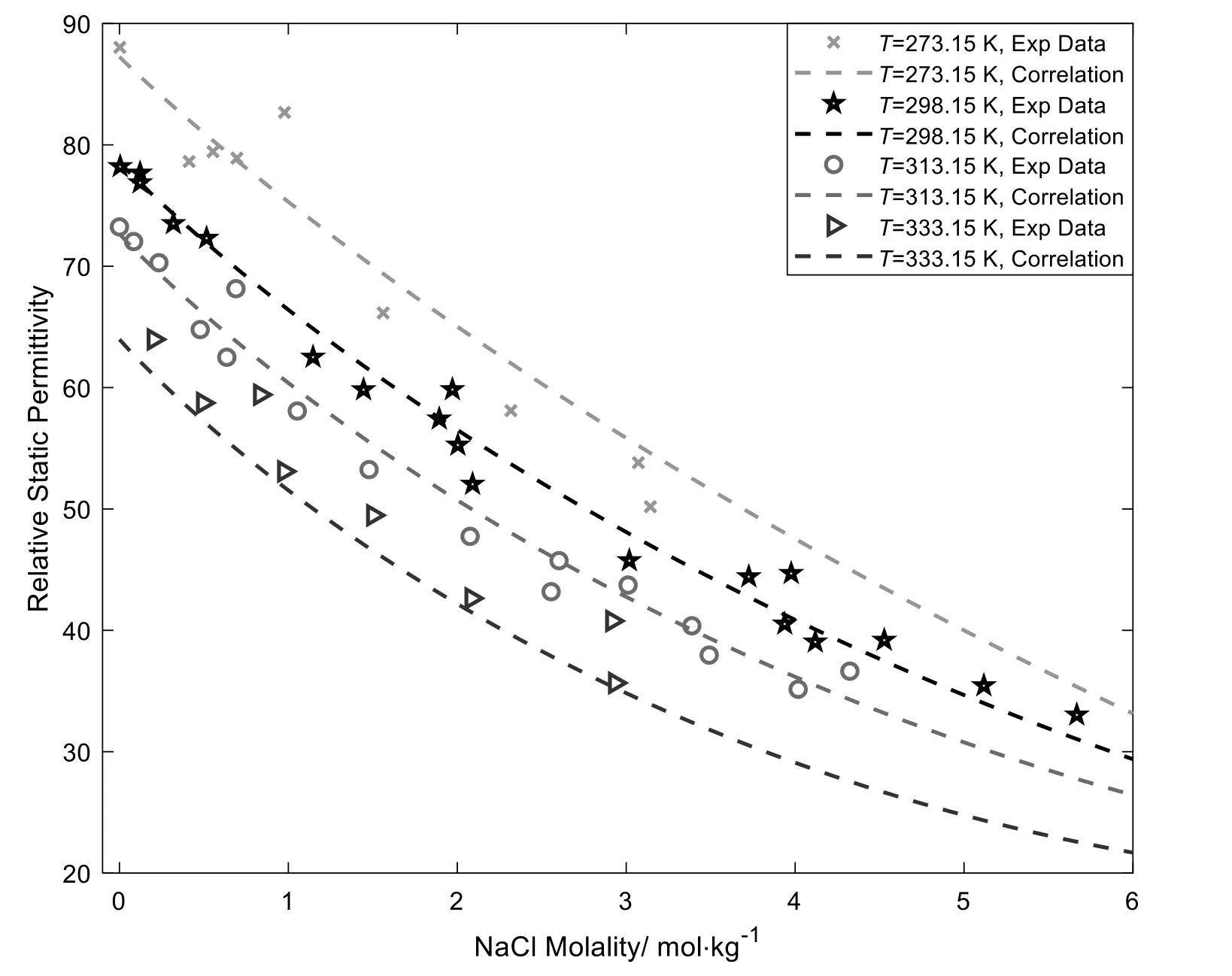
Fig.1.The relative static permittivity of aqueous NaCl solutions at different temperatures and molalities [24].

The objective function used for the regression is:

where NPis the number of data points,represents the calculated values(ACI,MIAC,liquid densities and gas solubilities),andrepresents the corresponding experimental values.

The results are typically presented as the relative average deviation (RAD):

For each H2O+electrolyte binary system,there are four adjustable parametersAfter modeling the H2O+NaCl binary systems,there are three adjustable parametersfor each H2O+gas+elec trolyte ternary system.

One binary systems is studied:H2O+NaCl,four gas-containing ternary systems are studied:H2O+carbon dioxide(CO2)+NaCl,H2-O+methane(CH4)+NaCl,H2O+nitrogen(N2)+NaCl,H2O+oxygen(O2)+NaCl.

3.Modeling Results

3.1.Results of binary systems

Before investigating the H2O+gas+electrolyte systems,the modeling of binary systems are considered,the binary systems contain H2O+gas and H2O+NaCl systems.The H2O+gas systems are modeled by using CPA in previous works.The CPA parameters of water and gases are from the literature [13,27],and are presented in Tables 1 and 2.In this work,we treat H2O as an association component with four association sites,CO2as not a selfassociating fluid.

In Table 1,Tcis the critical temperature,b is the CPA co-volume parameter,Γ is the CPA reduced energy parameter (Γ=a0/(Rb)),c1is the CPA alpha-function temperature-dependence,is the association volume,andis the association energy.

H2O is set to have a four-site (4C) scheme,and the three gases are set to non-association components.Before presenting the modeling results,it is necessary to review the two mechanisms of the gas dissolution:the vacancy (also called as insertion and hydrophobic) mechanism,and the solvation (also called as insertion-substitution and hydrophilic) mechanism.Table 2 lists the H2O-gas interaction parameters and modeling performance of gas solubilities in pure water.

In Table 2,kijin the binary interaction parameters between H2O and gas,T is the temperature,P is the pressure,NPis the number of data points.

The other binary system is the H2O+NaCl system.The cation/anion-water interaction parameters and CPA co-volume parameters of ions are obtained in regression.The regression progress is as follows:(1)obtaining cation/anion-water interaction parameter at reference temperatureand co-volume parameters of ions (bc/a) by fitting the experimental data of ACI (at 298.15 K),MIAC(at 298.15 K)and liquid densities of aqueous solutions(at 298.15 K);(2)obtaining temperature-dependent parameters of cation/anion-water interaction parameters ωc/a-water,TUc/a-waterfrom the regression of the experimental data of MIAC(over wide temperature ranges) and liquid densities of aqueous solutions(over wide temperature ranges).Table 3 and Fig.2 show the obtained parameters and the modeling results of H2O+NaCl binary system.

It can be observed from Table 3 that this model can correlate well the ACI,the MIAC and liquid densities over wide temperature-molality ranges.Fig.2 shows the activity coefficients of individual ions and salt in aqueous NaCl solutions.

Fig.2 shows that the MSA term and Born term have significant“opposing”values.The activity coefficient results can be explained as a balance of the positive Born contribution and the negative ionion contribution[18],the absolute value of these two contributions both increase with salt concentration increasing.

As discussed above,the “II+IW” theory ignores all physical interactions in aqueous electrolyte solutions,so,“II+IW” theory cannot accurately predict the activity coefficients.Our model considers the physical interactions,and give good agreements with the experimental activity coefficients.

Fig.3 shows that this model can correlate well MIAC of NaCl in aqueous solutions over wide temperature-molality ranges.We can also see from Fig.3 that the MIAC are different at different temperatures for a specific molality,so the temperature dependency of cation/anion-water interaction parameters cannot be ignored.

It can be observed from Fig.3 that,the deviations between experimental and calculated values are relatively large around molality=1.0 mol.kg-1water.That means our model cannot reproduce temperature dependency of MIAC around molality=1.0 mol.kg-1accurately.This is mainly because that the volume-exclusion is considered as temperature-independent in our model.Since the RAD of MIAC is accepted(3.6%)over wide temperature,to simplify the model,this current model use constant bc/aover wide temperature ranges.

Fig.4 shows the modeling results of liquid densities of aqueous NaCl solutions.From Fig.4,it can be observed that this model correlate well with the liquid densities of aqueous NaCl solutions over wide temperature ranges.As discussed above,in this work,we include the CPA co-volume parameters of ions (bc/a) into regression.The bc/aobtained in this work are smaller than those of Maribo-Mogensen et al.’s work [15] and Courtial et al.’s work[16],lower values of bc/arespect the correct volume-exclusion from ions.

3.2.Results of ternary systems

After obtaining the cation/anion-water interaction parameters and CPA co-volume parameter in binary system modeling,modeling of the ternary systems (i.e.H2O+gas+NaCl) is presented.At first,data selection of gas solubilities should be made,Duan and Sun [34],Yan et al.[35] reviewed experimental CO2solubilities in aqueous NaCl solution and pointed out the doubtful data.Duan et al.[36] reviewed the experimental CH4solubilities in aqueous NaCl solutions and pointed out the doubtful data.In this work,these mentioned low credibility experimental data are not included in modeling.The experimental solubilities of N2,O2in aqueous NaCl solutions are scattered and cover only limited ranges,so,we add all the founded data in modeling.The unit of NaCl concentration in some literature is“molarity”,in our calculations,we convert “molarity/mol.L-1solution” to “molality/-mol.kg-1water” before modeling.Table 4 and Figs.5–9 present the cation/anion-gas interaction parameters and the modeling performance for gas solubilities in aqueous NaCl solutions.

Table 4 summarizes the fitted adjustable parameters and model performance on gas solubilities.This model gives good agreements with experimental gas solubilities in aqueous NaCl solutions over wide temperature-pressure-molality ranges.

Table 1CPA parameters for pure components

Table 2Modelling performance of gas solubilities in pure water

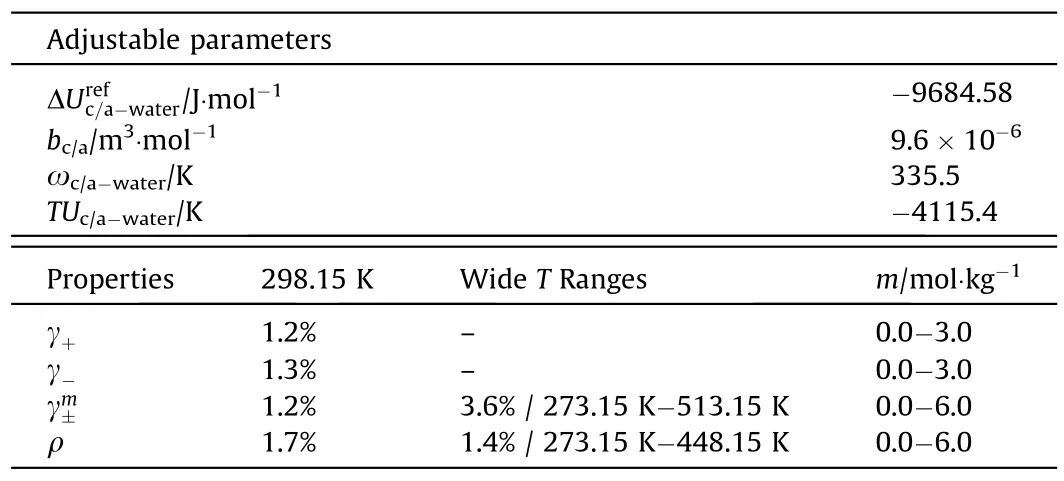
Table 3Adjustable parameters and modeling performance for H2O+NaCl system

Table 4Cation/anion-gas interaction parameters and modeling performance of gas solubilities in aqueous NaCl solutions

The deviations (RAD) are small for most investigated systems.The larger deviations of CH4solubility(RAD=7.3%)might be from high-temperature ranges (up to 513.15 K).

Fig.5 presents CO2solubilities in aqueous NaCl solution as a function of molality at different pressures.From Fig.5,we can see that CO2solubilities decrease as the increasing NaCl molality,NaCl shows significant salting-out effects on CO2.The reduction of gas solubility is due to the presence of ion solvation in a solvent:gas dissolution in water mainly because of the interstice of bulk water,the additive electrolytes form ion hydration,then,the interstice of bulk water will reduce,and more gas molecules will escape to vapor phase,result in low gas solubilities.

Fig.6 shows the solubilities of CH4in aqueous NaCl solution as a function of molality at different pressures.It can be seen from Fig.6 that this model can correlate well with the solubilities of CH4in aqueous NaCl solution.Similar to CO2,the solubilities of CH4decrease as the NaCl molality increases.It is also observed that the solubilities of CH4decreases as pressure decreases.

Fig.7 shows the modeling results of N2solubilities in aqueous NaCl solutions at 324.65 K.The results show that this model can correlate well N2solubilities in aqueous NaCl solutions.The N2solubilities increase with increasing pressures,and decrease with increasing molality,NaCl shows significant salting-out effects on N2in water.

Fig.8 shows the modeling results of O2solubilities in aqueous NaCl solutions at atmospheric pressure.The results show that this new model gives good agreements with experimental O2solubili-ties in aqueous NaCl solutions.The O2solubilities decrease with increasing temperatures,and decrease with increasing NaCl molality,NaCl shows significant salting-out effects on O2in water.

Some modeling works ignore the temperature dependency of salting effects.It is of interest to compare the results between the temperature-dependent approach and the temperatureindependent approach.Fig.9 shows the modeling results of O2solubilities in aqueous NaCl solutions using the temperatureindependent approach.

From Fig.9,it can be seen that the modeling results by using the temperature-independent approach are worse than those by using the temperature-dependent approach.As mentioned above,the salting-out effects are from the ion hydration.The ion hydration is affected by temperature changing,temperature-dependency of interaction parameters should be taken into account.

Different gases have different solubilities in the liquid phase,the solubilitiesin pure water follow a sequence of CO2>CH4>O2>N2with the same temperature and pressure.CO2has the biggest solubility because CO2is an acid gas;there is an additional equilibrium of two acids for the dissolution of CO2.

The solubilities of O2are about twice as high compared to N2at the same temperature and pressure[43].An explanation based on the hydrophobic mechanism[44]has been presented for this phenomenon:the McGowan volume of N2(22.22× 10-6m3.mol-1)is greater than that of O2(18.30×10-6m3.mol-1)[45],and the small hydrophobic solutes can enter the bulk water system without severely distorting the hydrogen-bonding network of the surrounding water,N2causes a greater distortion of this hydrogen-bonding network than does O2,leading to lower solubilities of N2[43].

CH4has a bigger volume (26.51 × 10-6m3.mol-1) than N2and O2,but CH4has bigger solubility than N2and O2,this is not consistent with the hydrophobic mechanism mentioned above.The possible explanations are that the C-H...O interaction is a hydrogenbonding [46] which is weaker than in the case of water,and CH4has the different molecular structure with N2and O2,i.e.having four carbon-hydrogen bonds.

It is of interest to compare the salting-out effects on different gases.In this work,we use Setschenow-type equation [47] to describe the salting-out effects:

Fig.2.Modeling performance of activity coefficients of ions and NaCl in aqueous solution.(a) Activity coefficients of cation [30].(b) Activity coefficients of anion [30].(c) Mean ionic activity coefficients [31].

Fig.3.Mean ionic activity coefficients of aqueous NaCl solutions at different temperatures and molalities [31].

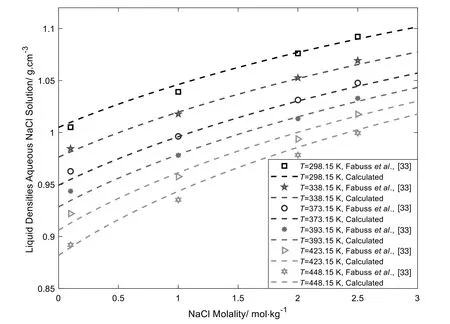
Fig.4.Liquid densities of aqueous NaCl solutions at different temperatures and molalities [33].

where S0is gas solubility in pure water(mol.kg-1),S is gas solubility in aqueous NaCl solution (mol.kg-1),kSis the Setschenow coefficients,m is the molality of salt (mol.kg-1).Fig.10 shows Setschenow coefficients (calculated from experimental data) for different gases.Because of the few data for different gases under the same pressure and temperature,we only list few data points here.

As discussed above,the salting-out effects of electrolytes mainly from the ion hydration.The solubility changes of CO2arefrom the combinations of additional acid equilibrium and ion hydration,and the solubility changes of CH4are from the combinations of C-H...O interaction and ion hydration.

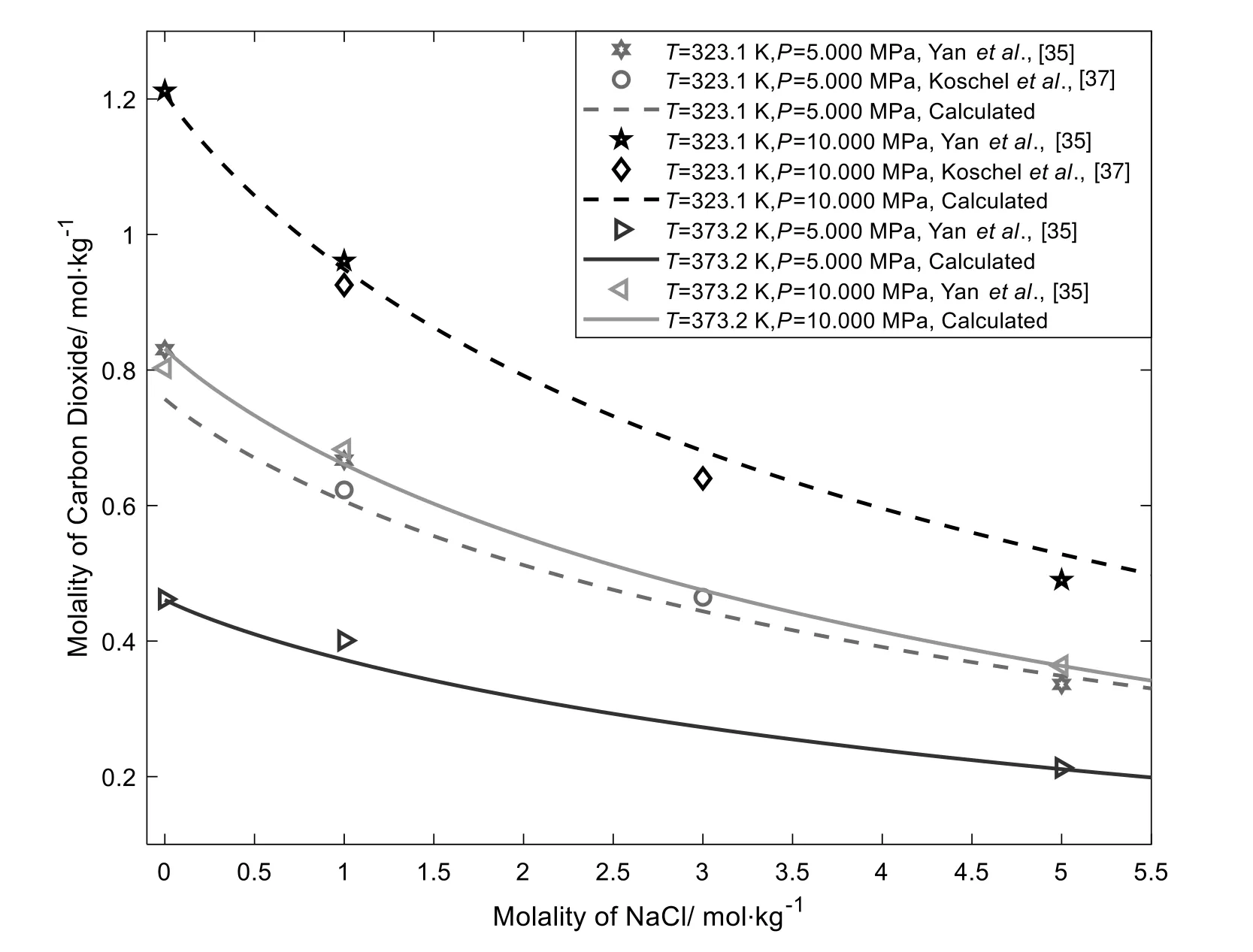
Fig.5.CO2 solubilities in aqueous NaCl solutions at 323.1 K and 373.2 K [35,37].

As can be observed from Fig.10,at 298.15 K and 101325 Pa,CO2has the smallest Setschenow coefficients,because additional acid equilibrium affects gas solubility more than ion hydration.CH4shows the unusual trend compared with other gases because of the weak C-H...O interaction.At 324.65 K and 20.265 × 106Pa,N2has bigger Setschenow coefficients than CH4.The Setschenow coefficients of CH4do not show an unusual trend at 324.65 K,mainly because that at the higher temperature,the C-H...O hydrogen bond has disintegrated.

In our model,we treat gases as no-association components,so,this model cannot describe the effects of C-H...O hydrogen bond on CH4solubilities.Furthermore,the chemical equilibrium is not included in this model;the additional dissolution equilibrium of acid gases (i.e.CO2) is not considered in this model.

Several e-EoS have been presented to model solubilities of CO2,CH4and N2in aqueous electrolyte solutions,it is of interest to compare the modeling performance of different e-EoS.Søreide and Whitson’s model [8] overpredicts CO2solubilities in pure water and NaCl solutions.Harvey and Prausnitz’s model [4],Aasberg-Petersen et al.’s model [7] overestimates gas solubilities (e.g.for CO2,RAD >10.0%) at high NaCl molalities.Zuo and Guo’s model[2] can only be applied at narrow temperature ranges.Sun et al.’s model [28] give relatively large deviations for solubilities of CO2and CH4at high temperatures.There are very few electrolyte EoS be applied to calculate solubilities of O2in aqueous NaCl solutions.Our model can be applied at high NaCl molalities (up to 6.4 mol.kg-1water),and give a good performance.At high temperature,the deviation of CO2and CH4is relatively large.

To better understanding and improving the models,a review and discussion of different e-EoS are needed.In these e-EoS,Zuo and Guo [2],Sun and Dubessy [10],Tan et al.[11] did not take the effect of salt presence on εrinto account.Harvey and Prausnitz[4],Aasberg-Petersen et al.[7],Haghighi et al.[14],Søreide and Whitson [8],and Maribo-Mogensen et al.[15] all take the effect of electrolyte presence on εrinto account.This treatment is crucial for electrostatic interaction calculations [17].Aasberg-Petersen et al.[7],Haghighi et al.[14],Sun and Dubessy [10],Søreide and Whitson [8] did not take the ion-water contribution.Simultaneously,The Born term is necessary for describing the salting-out effects and other phase behavior.Temperature dependency of salting effects is considered in some works [8,14,15].However,some models [2,4,7,12] ignored the temperature dependency of ion-gas interactions.Temperature dependency should be taken into account if the temperature range is wide.The salting-out effects result from ion hydration,and the temperature change influences ion hydration.Most models [4,7] present worse performances at high molality.The reason may be that all these models considered electrolytes dissolving completely in water in water,and the ion pair is not considered.

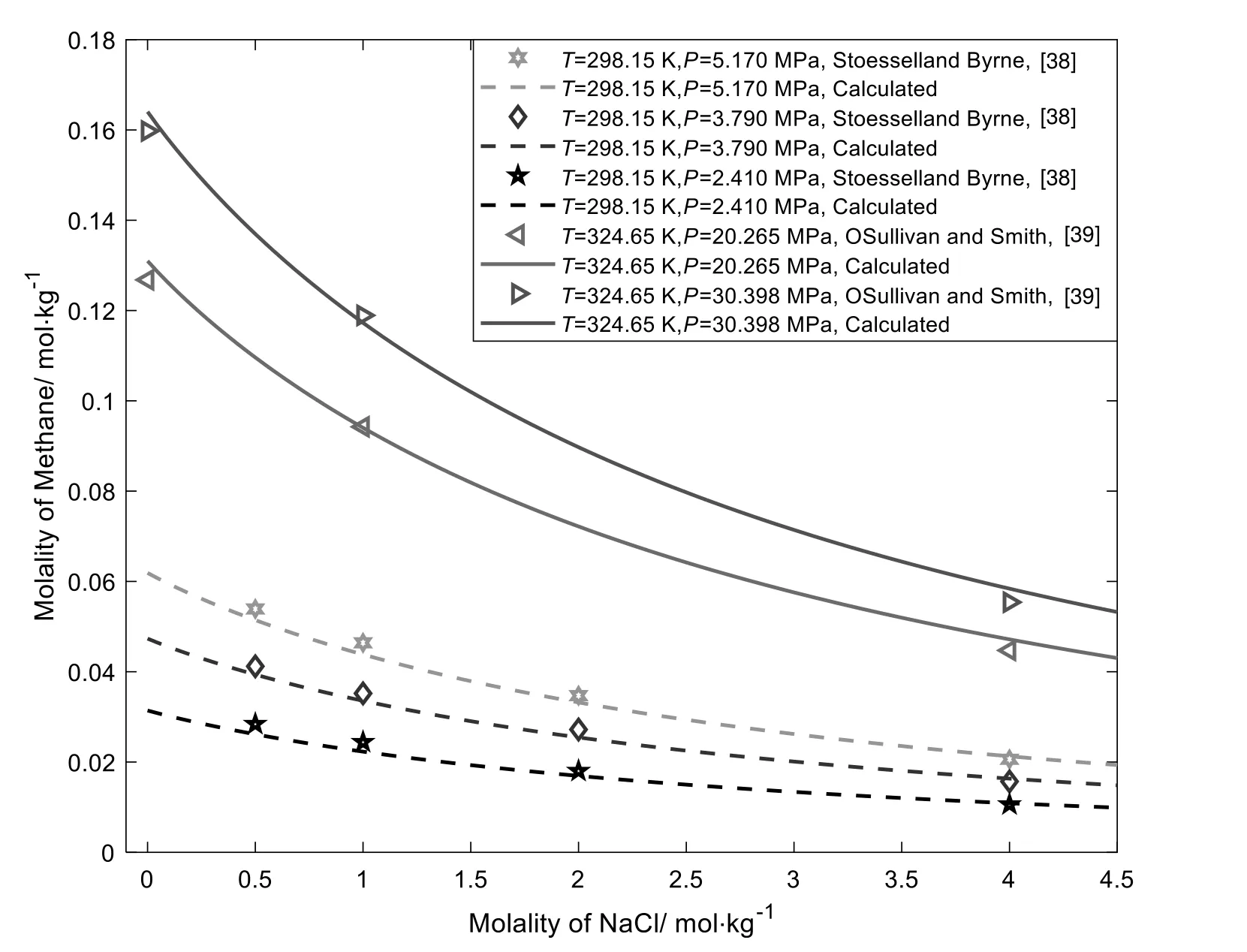
Fig.6.CH4 solubilities in aqueous NaCl solutions at 298.15 K [38] and 324.65 K [39].

Fig.7.N2 solubilities in aqueous NaCl solutions at 324.65 K [39].

Our model does not take into account any chemical equilibrium;in other words,ion-association,additional chemical equilibrium of acid gas and weak-acid anion dissolution in water are not included in the model.This current model considers all gases as non-association components,it is recommended for modeling of strong-electrolyte systems,non-acid-gas systems,and nonassociation-gas systems.

Fig.8.O2 solubilities in aqueous NaCl solutions at 101325 Pa [40-42].

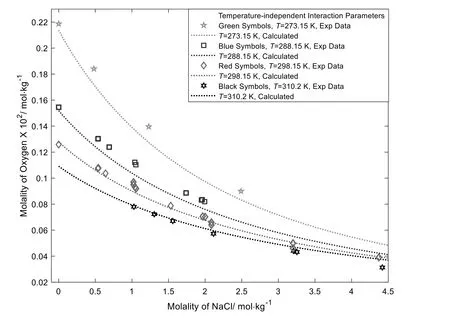
Fig.9.Calculations of O2 solubilities in aqueous NaCl solutions [40-42] by using the temperature-independent approach.

Fig.10.Setschenow Coefficients for gases in aqueous NaCl solutions [39,41,48,49].

4.Conclusions

A new electrolyte Equation of State has been presented for modeling the phase equilibrium and volumetric properties for aqueous electrolyte solutions.The two main innovation points of this model are accurate predictions of ACI and liquid densities.The H2O+NaCl binary system,H2O+gas+NaCl ternary systems have been correlated using this new model.The modeling results show that this new model gives accurate agreements with the experimental ACI,MIAC,and liquid densities of aqueous NaCl solutions.With temperature-dependent interaction parameters,this new model gives good agreements with the experimental gas solubilities over wide ranges of temperature,pressure and NaCl molality.The experimental volumetric properties,relative static permittivity are critical for modeling aqueous electrolyte solutions.More experimental data over more extensive temperaturepressure-molality ranges would be useful for the investigation of aqueous electrolyte solutions.Adding chemical equilibrium and considering hydrogen-bonding of gases are potential solutions for improving the modeling performance.Furthermore,more theoretical studies of ACI may result in developments towards better approaches.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors thank the Department of Chemical and Biochemical Engineering at Technical University of Denmark,College of Mechanical and Electrical Engineering at Hohai University,and School of Energy and Power Engineering at Wuhan University of Technology for supporting this research.

Nomenclature

AAssocresidual Helmholtz energy contribution for association

ABornresidual Helmholtz energy contribution Born hydration model

AMSAresidual Helmholtz energy contribution from the Mean Spherical Approximation

AResresidual Helmholtz energy

ASRKresidual Helmholtz energy contribution for the cubic Soave Redlich Kwong EoS

a SRK temperature dependent energy parameter

aiSRK temperature dependent energy parameter of component i

b CPA co-volume,m3.mol-1

biCPA co-volume of component i,m3.mol-1

c1pure component temperature-dependent parameter for Soave’s α(T)-function

d average diameter of cation and anion,m

didiameters of ions i,m

e the elementary charge

gE，∞excess Gibbs energy at infinite pressure

kijbinary interaction parameter between solvent and gas

kSSetschenow coefficient

m molality of salt,mol.kg-1

NAAvogadro constant

NPnumber of data points

niamount of component i

P pressure,pressure range,Pa

R ideal gas constant

rBorn，iborn radius of the ion i,m

rPauling，iPauling radius of ion i,m

S molality of gas in aqueous NaCl solutions,mol.kg-1

S0molality of gas in pure water,mol.kg-1

T temperature,temperature range,K

Tccritical temperature,K

Trefreference temperature,298.15 K

TUijan adjustable parameter of the temperature dependency,K

V volume,m3

ΔUijchange in interaction energy between like and unlike interactions

ximole fraction of component i

Zicharge of ion i

αjiNRTL non-randomness parameter

Γ CPA reduced energy parameter,K

γ+activity coefficient of cation

γ-activity coefficient of anion

εrstatic permittivity relative to vacuum

ε0vacuum permittivity

κ inverse Debye length,m-1

ρ density of fluid,kg.m-3

ωijlinear dependency in interaction energy calculation,K