HE Yining， GUO Qi

（School of Mathematical Sciences，SUST，Suzhou 215009，China）

Abstract： In this paper，we introduced a kind of spherical translations and established some theorems of Helly type for spherically convex sets concerned with these spherical translations. The conclusions obtained here are analogues of those for convex sets in spherical spaces. This contributes to the further study on spherical convexity.

Key words： spherically convex set；spherical translation；Helly theorem CLC number： O18 MR（2010） Subject Classification： 52A55 Document code： A Article ID： 2096－3289（2021）04－0023－07

1 Introduction

The study on convexity theory in spherical spaces has been getting more and more attentions in the recent decades （see [1-2] and the references therein）. The goal of such a study is to establish a systematic theory parallel to the convexity theory in Euclidean spaces，including the basic theories of spherically convex sets and spherically convex functions （see e.g. [1-5]），the spherical convex geometric analysis （see [6-7] and the references therein） and the applications of spherical convexity theory （too many references to mention here，so，readers are referred to the references in e.g. [1－2]）.

Due to the lack of compositions and transformations on spheres，the development of spherical convexity theory is very slow in the past century. In fact，the convexity theory in spherical spaces emerged almost at the same time as the one in Euclidean spaces （[8-9]）. However，the earlier work was concentrated only on the combinatorial properties of spherically convex sets，or more precisely，only on the establishment of theorems of Helly type with various kinds of spherically convex sets （see e.g.[10-13]） simply because the definitions of spherically convex sets could be given only in geometric languages in the earlier time. The theorems of Radon type and Carathéodory type for spherically convex sets are established very lately in [4] after [4-5] formulated an equivalent definition of analytic form.

The classical Helly theorem for convex sets in the n-dimensional Euclidean space is well-known，which states that if any n+1 elements in a finite family of convex sets have a common point，then all elements in the family have a common point（see [14] or[15]）. The analogues of the classical Helly theorem were also established repeatedly for various kinds of spherically convex sets （see e.g.[4，8，10-13]），and we would like to point out that the argument in [4] is the only one with analytic nature.

As known，the various extensions，generalizations and ramifications of the classical Helly theorem for convex sets form a powerful systematic tool in combinatorial and convex geometry，etc. So it is reasonable to find the analogues of these extensions，generalizations and ramifications for spherically convex sets. However，as far as we know，there are almost no such results available in the literature. The cause of such a phenomenon is simply that there are not so many compositions and transformations on spheres，which even make it impossible to formulate such extensions，generalizations and ramifications. As a try，in this article we will introduce a kind of spherical translations and establish several theorems of Helly type for spherically convex sets concerned with these spherical translations.

2 Notation and definitions

As usual，Rnand Sn-1denote the n-dimensional Euclidean space and the unit sphere in Rnrespectively.“〈·，·〉” and ｜｜·｜｜denote the standard inner product and the norm induced by “〈·，·〉” on Rn，respectively. Often Rnis also viewed as an affine space，so，in this paper，the vectors and the points will not be distinguished intentionally. We use x，y，z，… to denote the points （or vectors） in Rnand u，v，w，… to denote points （or unit vectors） in Sn-1. The letter o always stands for the origin （or zero vector） of Rn. R，R+and R*+stand for the set of reals，nonnegative reals and positive reals respectively.

A set of the form V∩Sn-1is called a k-sphere （0≤k≤n-1），where V is a （k+1）-dimensional subspace of Rn. Observe that a 0-sphere is of the form {x，-x} for some x∈Sn-1. A set of the form Su+:=Hu+∩Sn-1（resp. Su+:=Hu+∩Sn-1） is called an open （resp. closed） hemisphere （Su-and Su-are defined in a similar way）. u，v∈Sn-1are called （a pair of） antipodes （or antipodal） if v=-u. For other notation refer to [15].

As mentioned in introduction，various distinct spherical convexities were defined and studied in the history（see，e.g. [8-12] and the references therein），which lead to different families of spherically convex sets. We point out that except the one in [4] or [5] all other definitions were given in geometric languages. Here，following [2]，we adopt the one given in [1] or [3] but with an equivalent definition of analytic form.

The radial projection ρ:Rn→Sn-1∪{o} defined as

is crucial in the definition of analytic form. The following properties of radial projection are trivial：

（i） ρ °ρ=ρ，where ° denotes the composition of operators；

（ii） ρ（tx）=ρ（x），ρ（-x）=-ρ（x） for x∈Rnand t∈R*+；

（iii） ρ（x）=x if and only if x∈Sn-1or x＝o.

With the help of radial projection，a spherical addition “+s”on Rnwas introduced in [4－5] as：x+sy:=ρ（x+y），x，y∈Rn. Naturally，the spherically convex combination composition was also introduced in [4－5]：

is called a spherically convex combination （an s-convex combination for brevity） of x1，x2，…，xk. When k＝2，we write λx+s（1-λ）y instead of （s）（λx+（1-λ）y）.

Definition 1 A set C⊂Sn-1is called spherically convex（s-convex for brevity） if for any w1，w2∈C and 0≤λ≤1，λw1+s（1-λ）w2∈C whenever λw1+（1-λ）w2≠o.

An s-convex set is called proper if it contains no antipodes.

For C⊂Sn-1，denote by RC:=R+C its radial hull，which is clearly a cone. Then，in the recent decades，a popular definition of spherically convex sets is that C⊂Sn-1is called a spherically convex set if RCis a convex cone，i.e. RC=coneC，the convex cone generated by C （see [1，3]）. The following proposition was proved in [2，4]，which implies that the popular definition above is equivalent to Definition 2.1（see[2，4] for the proofs，or check directly）.

Proposition 2 Let C⊂Sn-1. Then C=RC∩Sn-1and

（i） C is a （closed） s-convex set if and only if RCis a （closed） convex cone.

（ii） C is a proper s-convex set if and only if the convex cone RCis pointed，i.e. RC∩（-RC）={o}.

3 Gnomonic map and spherical translations

The well known gnomonic map from an open hemisphere to an Euclidean space is a very important tool in the study on spherical convexity. In this section，we recall some properties of gnomonic maps，and then define and study the so-called spherical transformations. Following the custom，we denote Hvby Rvn-1（or simply Rv） to emphasis the fact that Hvis actually an （n-1）-dimensional Euclidean space.

Definition 2 Let v∈Sn-1. Then the map gv:Sv+→Rvdefined by

By Proposition 3，the following corollary is obvious.

Corollary 1 Let C⊂Sv+. Then C is s-convex if and only if gv（C）⊂Rvis convex，where gv（C） denotes the image of C under gv.

In fact，since both gvand gv-1are continuous，we may easily regain the following conclusions of [6].

Proposition 4 Let v∈Sn-1. For every C⊂Sv+，we have

（i） gv（C）⊂Rvis a convex body if and only if C is a s-convex body，i.e. gv:K（Sv+）→K（Rv） is a bijection，where K（Rv） denotes the set of convex bodies contained in Rv.

（ii） If S⊂Sn-1is a k-sphere，0≤k≤n-2，with （the k-hemisphere） S∩Sv+≠Ø，then gv（S∩Sv+）⊂Rvis a kaffine subspace；Conversely，if V⊂Rvis a k-affine subspace，then gv-1（V）⊂Sv+is a k-hemisphere. Moreover v∈S∩Sv+if and only if gv（S∩Sv+） is a linear subspace.

With the help of Proposition 4，we may define the counterpart of translations on Euclidean spaces for every open hemisphere Sv+.

Definition 3 Let v∈Sn-1. For each translation Lb（·）:=·+b on Rv，where b∈Rv，the operation Lb:Sv+→Sv+defined by

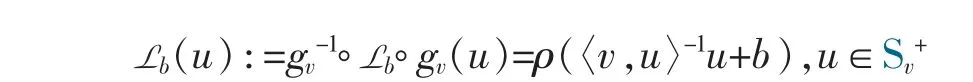
is called a spherical translation （s-translation for brevity） on Sv+，where “°” denotes the composition of operators.

Since Lbis closedness-preserving and convexity-preserving，by Proposition 3 and 4，the following conclusionis straightforward.

Proposition 5 Let C∈Kp（Sv+）. Then for every b∈Rv，Lb（C）∈Kp（Sv+），i.e. Lbis closedness-preserving and s-convexity-preserving.

Denoting by L（Sv+） the set of s-translations on Sv+，we have the following Theorem.

Theorem 1 Let v∈Sn-1. Then，

（i） Lb°Lc=Lb+cfor all Lb，Lc∈L（Sv+）. Hence，L（Sv+） is an abilian group under the compositions of operators，Moreover，the identity of L（Sv+） is Lo，and Lb-1=L-b.

（ii） The map ψ（Lb）:=Lbis a group isomorphism from L（Sv+） onto L（Rv）:={Lb|b∈Rv}.

Proof. Since L（Rv） is an abelian group and Lb°Lc=Lc°Lb=Lb+cfor all b，c∈Rv，we need only to check Lb°Lc=Lb+c. Indeed，by definition

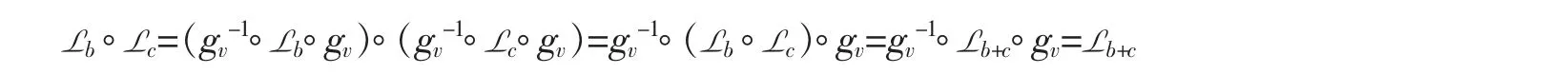
The similar argument for Lc°Lb=Lb+cworks as well. The proof completes. □

4 Some theorems of Helly's type for s-convex sets

In this section，we will establish several theorems of Helly's type，concerned with s-translations，for s-convex sets.

Theorem 2 Let C，C1，C2，…，Cm∈Kp（Sv+）. If for arbitrary i1，i2，…，in∈{1，2，…，m}，there is b=bi1，…，in∈Rvsuch that LbC∩Cij≠Ø，j=1，2，…，n，then，there exists b*∈Rvsuch that

Proof. Let D:=gv（C），Di:=gv（Ci） and then define

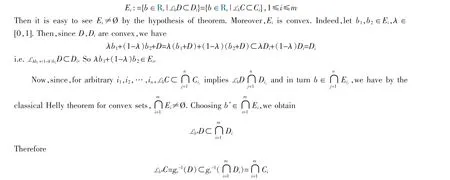
Also，Theorem 3 reduces to Theorem 4.3 in [4] when C is a singleton. The following theorem of Helly type is the dual of Theorem 3，which can be obtained by applying Theorem 3 trickily to the family of polar s-convex sets（the polar set C⊥of an s-convex set C is defined as{u∈Sn-1|〈u，w〉≤0 for all w∈C}，which is an s-convex set as well）. However，we prefer to present a direct argument here.

The proof is complete. □

Final Remark The main contributions of this paper are the introduction of s-transformations and the establishment of several theorems of Helly type concerned with such s-translations. Of course，the s-translations defined here are not so satisfactory as one expects since they can move sets around only in a hemisphere. So，our next research topic is to find more general translations on the whole sphere and in turn more general extensions of Helly's theorem.