JIAO Xiaoxiang，XIN Jialin

(School of Mathematical Sciences, University of Chinese Academy of Sciences，Beijing 100049, China)

Abstract We present a construction of the complex Grassmannian G(2,n+2) as a quotient of some minimal submanifold Qn+1 of HPn+1, then show that a surface in G(2,n+2) can be horizontally lifted to Qn+1 if and only if it is totally real.

Keywords Grassmannian; totally real surface; horizontal lift

The theory of minimal surfaces is an important part of modern differential geometry. The theory is particularly fruitful when the ambient space is a symmetric space. Calabi[1]proved a rigidity theorem for minimal two-spheres of constant curvature inSn. Bolton et al.[2]constructed all the minimal two-spheres of constant curvature inPn, and showed that a totally real minimal two-sphere inPncan be mapped, by a holomorphic isometry ofPn, intoPn⊂Pn. Then He and Wang[3]proved a similar rigidity result for totally real minimal two-spheres in HPn.

In this paper, we present a construction of the complex GrassmannianG(2,n+2) due to Berndt[4], which considersG(2,n+2) as a quotient of some minimal submanifoldQn+1of HPn+1. A Riemannian metric can be given onG(2,n+2) so that the projection π:Qn+1→G(2,n+2) is a Riemannian submersion. Then we show that a surface inG(2,n+2) can be horizontally lifted toQn+1if and only if it is totally real.

Our result is a special case of Ref.[5], where the author considered a general Riemannian submersionN→B, and characterized the existence of horizontal lifts of a submanifold ofBusing a familyJof (1,1)-tensors onB. In our paper, we make use of the fact that the projectionQn+1→G(2,n+2)is a principal bundle, thus obtain a characterization by a first order PDE. Our method is largely inspired by Ref.[3], where the authors considered the Riemannian submersionS4n+3→HPn.

1 Preliminaries

i2=j2=k2=-1,

ij=k=-ji,jk=i=-kj,ki=j=-ik.

Thus H is associative but not commutative.andare naturally embedded into H as follows:

=·1⊂H, C=·1⊕·i⊂H,

and we sometimes express an element of H asq=z+wj, wherez,w∈C.

Conjugation is defined for quaternions:

Or equivalently,

Let Hnbe the space ofn-dimensional quaternion column vectors. We consider it as a right H-module. Ifp=(p1,…,pn)T,q=(q1,…,qn)T∈Hn, two inner products ofp,qare defined:

It is easily verified that 〈,〉is just the usual Euclidean inner product if Hnis identified as4n, and that the following properties hold:

wherep,q∈Hn,x,y∈H.

Similarly, forz=(z1,…,zn)t,w=(w1,…,wn)t∈n, we define their inner products:

We will often omit the subscriptsand H for simplicity.

Next we consider the quaternion projective space HPn, the set of quaternionic lines in Hn+1. Equivalently, HPn=S4n+3/Sp(1), whereS4n+3is the unit sphere in Hn+1≅4n+4, andSp(1), the multiplicative group of unit quaternions, acts onS4n+3by right multiplication. Since this is an isometric action, there is a unique Riemannian metric on HPn, called the Fubini-Study metric, such that the quotient mapτ:S4n+3→HPnis a Riemannian submersion. For anyq∈S4n+3, letHqbe the horizontal space ofτatq, i.e. the normal space to the fibreτ-1(τ(q)). ThenHq={q′∈Letτq=dτq|Hq. By assumption,τq:Hq→Tτ(q)HPnis a linear isometry.

2 The submanifold Qn+1⊂HPn+1; the complex Grassmannian G(2,n+2)

We quote some results from Ref.[4].

SU(n+2)acts onS4n+7⊂Hn+2isometrically via

SU(n+2)×S4n+7→S4n+7,

wherez,v∈n+2, with|z|2+|v|2=1. This action commutes with theSp(1)-action onS4n+7defined in the last section, hence descends to an isometric action on HPn+1.

By some straightforward calculations, we find that thisSU(n+2)-action on HPn+1has only two singular orbits, namely,

Pn+1={τ(z+0·j)|z∈S2n+3},

(1)

and

v∈S2n+3,〈z,v〉=0}，

(2)

whereS2n+3is the unit sphere ofn+2.

We have the following proposition from Ref.[4]:

Proposition2.1The singular orbits of theSU(n+2)-action on HPn+1arePn+1andQn+1.Qn+1has codimension3 in HPn+1, and is isometric to the homogeneous spaceSU(n+2)/SU(2)×SU(n) equipped with a suitable invariant metric. Furthermore,Qn+1is a minimal submanifold of HPn+1.

Now consider an action ofU(1) onQn+1:

wheret∈. Again this is an isometric action. A vector fieldξonQn+1is defined:

=dτq(iq)=τq(iq).

(3)

LetBn+1=Qn+1/U(1). SinceU(1) acts onQn+1isometrically, there is a unique Riemannian metric onBn+1such that the natural projectionπ:Qn+1→Bn+1is a Riemannian submersion.

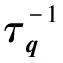
(4)

(5)

Since by definitionTτ(q)Qn+1=·ξτ(q)⊕τ(q), this completely determinesφ. In particular,φ()⊂.

G(2,n+2)=U(n+2)/U(2)×U(n),

where the metric onG(2,n+2)is induced by the following bi-invariant metric onU(n+2):

Thus, for example,B2is isometric toG(2,3)=CP2, with the Fubini-Study metric of constant holomorphic sectional curvature 8.

RemarkThe isometry betweenG(2,n+2) andBn+1can be explicitly given as

G(2,n+2)→Bn+1,

wherez,v∈Cn+2,|z|=|v|=1,〈z,v〉=0.

3 The main theorem

Definition3.1SupposeNis a Hermitian manifold,Jis its complex structure,f∶M→Nis an immersion from a surfaceMtoN. Thenfis called totally real ifJImf*p⊥Imf*pfor allp∈M.

If we choose a local frameX,YforM, thenfis totally real if and only ifJf*X⊥f*Yeverywhere. This follows easily from the Hermitian condition 〈Ju,Jv〉=〈u,v〉,J2=-1, where 〈,〉 is the Riemannian metric onN.

Now we can state our main result.

Theorem3.1SupposeMis a surface,ψ:M→Bn+1an immersion, then the following are equivalent:

1)ψis totally real;

Furthermore,ηis minimal inQn+1if and only ifψis minimal inBn+1.

We prove the theorem step by step.

Step1LetUbe an open subset ofM,η:U→Qn+1an immersion, we shall find a sufficient and necessary condition forηto be horizontal.

dη=dτdq

=dτ(dq-q〈q,dq〉)，

(6)

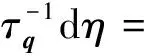
Recall from the last section that

ηis horizontal with respect toπ

⟺〈dq-q〈q,dq〉,iq〉=0

⟺〈dq,iq〉=0.

For the last equivalence note thatq∈τ-1(Qn+1) implies 〈q,iq〉=0.

Then

〈dq,iq〉=0

⟺0 =〈dZ+dV·j,Zi+Vk〉

=(〈dZ,Z〉-〈V,dV〉)i+

(〈Z,dV〉+〈dZ,V〉)k

=(〈dZ,Z〉+〈dV,V〉)i.

In summary, we have proved

〈dZ,Z〉+〈dV,V〉=0.

(7)

Step2Letψ:M→Bn+1be an immersion of a surfaceMintoBn+1. We look for the condition under whichψhas a local horizontal lift toQn+1.

(8)

Sinceη0is horizontal, we apply Lemma 1 to obtain

0=〈d(λZ),λZ〉+〈d(λV),λV〉

=〈dλ·Z+λdZ,λZ〉+〈dλ·V+λdV,λV〉

2d(logλ)=〈dZ,Z〉+〈dV,V〉.

(9)

If we take a local coordinate (x,y) onM, this amounts to

(10)

that is,

holds. This equation simplifies to

〈Zx,Zy〉+〈Vx,Vy〉=〈Zy,Zx〉+〈Vy,Vx〉.

(11)

Thus we obtain

We have

dψ=dπdτdq

=dπdτ(dq-q〈q,dq〉-iq〈iq,dq〉)

(12)

Choose a local coordinate (x,y) onM. Then, using the definitions of the tensorsφ,J(see (5)), and the fact thatτ,πare Riemannian submersions, we obtain

ψis totally real

⟺0 =〈ψx,Jψy〉Bn+1

(13)

=〈qx-q〈q,qx〉-iq〈iq,qx〉,iqy-iq〈q,qy〉+q〈iq,qy〉〉

=〈qx,iqy〉-〈qx,iq〉〈q,qy〉+〈qx,q〉〈iq,qy〉-

〈qx，q〉〈q,iqy〉-〈qx,iq〉〈iq,qy〉-

〈qx，iq〉〈iq,iqy〉+〈qx,iq〉〈q,qy〉

=〈qx，iqy〉-〈qx,q〉〈q,iqy〉-〈qx,iq〉〈iq,iqy〉

For the second step note thatq∈τ-1(Qn+1)implies 〈q,iq〉=0. Differentiating〈q,q〉=1 yields

0 =〈qx,q〉+〈q,qx〉

i.e.,〈qx,q〉∈ImH. Similarly, differentiating〈q,iq〉=0 yields

i.e.,〈q,iqy〉∈. Therefore〈qx,q〉〈q,iqy〉∈ImH. Similarly 〈qx,iq〉〈iq,iqy〉∈ImH. Thus we get

=2Re〈qx,iqy〉

=Re〈Zx+Vxj,Zyi+Vyk〉

=Re(〈Zx,Zy〉i-〈Vy,Vx〉i)

=Im(〈Vy,Vx〉-〈Zx,Zy〉).

(14)

Finally, from (13) and (14) we obtain

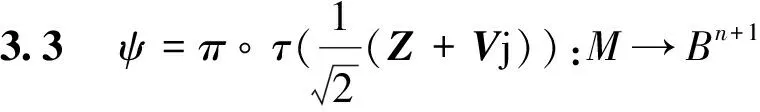
Im(〈Vy,Vx〉-〈Zx,Zy〉)=0,

or equivalently,

〈Vy,Vx〉-〈Zx,Zy〉=〈Vx,Vy〉-〈Zy,Zx〉.

(15)

Comparing with Lemma 3.2, we find thatψhave a local horizontal lift toQn+1if and only if it is totally real.

Step4We need a simple lemma.

(16)

Comparing with the Gauss equation inN, we find that

(17)

The conclusion follows immediately.

□

From the above lemma, we see that

This applies to our situation and the main theorem is fully proved.