张雷雷, 解 龙, 高 旭, 孙天宇, 张 峰

(1.西安现代控制技术研究所, 陕西 西安 710065; 2.西北工业大学 力学与土木建筑学院, 陕西 西安 710129)

0 引 言

随着近年来常规弹药向多用途和智能化扩展,其高成本使得可靠性鉴定试验难以采用普通弹药的大样本量考核方式[1-2]。目前在小子样系统可靠性评定领域,由于贝叶斯理论能够有效整合验前试验信息与现场试验信息,并对系统可靠性作出客观评价,取得了不少有意义的研究成果[3-11]。如文献[3]提出一种改进美国陆军装备系统分析中心增长模型的可靠性贝叶斯评定方法,并成功应用于某数字控制系统;文献[4]针对复杂液体推进系统提出了基于马尔可夫链蒙特卡罗法的贝叶斯评估方法,有效解决了贫信息下可靠性评估困难的问题;文献[5]提出借助最大熵方法对验前分布进行确定,然后再进行可靠性评定的方法;文献[6]以某航天系统为研究对象,提出融合多源信息和专家知识的贝叶斯可靠性评估方法;文献[7]基于贝叶斯理论提出了对航空发动机涡轮盘的可靠性评定方法,取得了有效的评定结果;文献[8]针对小样本情形下零失效型部件的可靠性评估问题,基于威布尔模型和贝叶斯理论建立了综合可靠性评估模型及求解方法;文献[9]将模糊数学和灰色系统理论引入贝叶斯网络模型中,提出了一种基于不确定隶属度函数和区间特征量的复杂不确定系统可靠性分析方法;文献[10]针对高可靠、长寿命产品的可靠性评估,提出了一种无失效数据下的贝叶斯估计方法,在保证评估精度的情况下显著降低了样本量;文献[11]结合动态离散时间贝叶斯模型和故障树模型,解决了不确定条件下的动态系统可靠性评估问题,并成功应用于动车制动系统。

虽然应用贝叶斯理论进行小子样可靠性评估已得到了工程界的普遍共识,但在验前信息与现场信息“异母体”下的有效折合及验前信息为多源情形下的贝叶斯验前分布构建方面,依然是目前难点所在[6-13]。诸多学者所提方法不一,总体来说与所研究对象关联性较强,呈现一定程度的“案例式”研究特点,无法直接应用于高价值弹药领域。弹药研制过程中,其技术状态会经历原理样机、工程样机等阶段,试验环境会与实际工作环境有所差异,与已定型相似装备会存在一定功能和硬件的沿用[2]。这些特点使其可靠性特征具有时间上的动态特性、环境上的差异特性和对象上的关联特性,现有方法难以充分挖掘和利用这些特性背后所关联的样本量数据以有效补充小容量现场样本,因此需要探究新的高效可靠性评定方法。

著名科学家钱学森于上世纪七十年代提出“小子样变动统计”[14-15]的概念,为少量试射情况下对武器装备的精度指标进行评估和鉴定提供了思路。其概念可近似归纳如下:对于多个相互关联的不同总体,例如具有不同来源的多组样本,或者同一对象在不同阶段、不同时段所生成的样本,通过统计建模和参数估计获得关于某一总体的更多知识或各个总体之间的内在关联和变动关系,完成统计推断、趋势预测、统计决策等。高价值弹药的样本特征具备小子样变动统计的特点,因此可借助小子样变动统计的思想进行可靠性综合建模和分析。但该思想发展至今,由于缺乏系统的理论基础,还未形成成熟的方法体系,目前明确提出“小子样变动统计”这一术语并进行相关研究的文献还较少,因此如何基于小子样变动统计思想对高价值弹药可靠性进行建模将是本文的研究重点。

本文拟采用“小子样变动统计”思想建立高价值弹药的可靠性综合评定模型,将不同研制阶段、环境鉴定试验、已定型相似装备外场使用等获得的成败型统计数据作为历史样本,引入信息熵和条件熵理论对历史样本与现场小容量样本在“异母体”下的多源数据融合进行研究,获得各类历史样本的融合权重。构建多源混合先验分布,基于融合验前分布和现场样本,推导得到失效概率的贝叶斯验后分布,从而实现对高价值弹药可靠性置信下限的贝叶斯统计推断。最后,以某型高价值弹药为应用对象,验证了本文方法的有效性和合理性。

1 可靠性建模

1.1 弹药装备研制中存在的变动统计问题

弹药装备在研制过程中会经历原理样机、工程样机等典型阶段,每个阶段都会开展一定量的外场发射飞行试验,因此积累了可一定程度上表征可靠度的样本数据,但由于每个阶段伴随有部分设计上的优化迭代,使其与最终项目定型时的样本特征有一定差异;工程样机阶段弹药会经历一系列环境鉴定试验,如高温、低温、湿热等典型单应力环境,因此会积累一定量的样本数据,而弹药的可靠性特征与所处环境密不可分,在不同的环境条件下会呈现出不同的水平;武器装备的研制普遍具有一定继承性,弹药类产品更是如此。部分弹上部件通常沿用其他已定型相似弹药的技术成熟产品或货架产品,而相似弹药在定型及部队演习过程中已积累较多的外场靶试数据,一定程度上可以反映当前在研弹药组成部件的可靠性水平。

上述3种情况分别体现了弹药可靠性在研制阶段上呈现的动态特性、环境上呈现的差异特性和相似装备上呈现的关联特性。这些特性背后所关联的的三类历史样本与待鉴定弹药定型时的现场样本在可靠性特征上存在较多相似性,但又有一定差异性,因此高价值弹药的可靠性综合评定属于典型的小子样变动统计范畴。

1.2 基于小子样变动统计的弹药可靠性建模

将待鉴定弹药的可靠性特征在时间上具有的动态特性、环境上具有的差异特性、对象上具有的关联特性分别记为X、Y、Z,则弹药的可靠性函数可记为

R=Φ(X,Y,Z)

(1)

将待鉴定弹药的研制阶段划分为A,B,…,表示原理样机阶段、工程样机阶段等不同的研制阶段,不同阶段的外场飞行试验样本量记为[(nA,xA),(nB,xB),…],其中n为试验总数,x为试验成功数。

LM法[4]是由Lindstorm和Madden提出的近似方法,适用于多个部件(或子系统)串联组成的系统。若某系统由m个子系统组成,第j子系统在nj次试验中有rj次失效、xj次成功,则系统可靠性RS的极大似然估计为

(2)

(3)

最后,针对不同历史样本与现场样本之间“异总体”问题,引入相似系数ρ表征各历史样本向现场样本的接近程度,则式(1)可进一步表征如下:

(4)

式中:n*,x*分别为现场试验数和现场成功数。

由此便得到了弹药装备基于小子样变动统计的可靠性模型,关于相似系数ρ和可靠性特征量R的确定,下文将分别引入条件熵理论和贝叶斯理论进行研究,最后基于实际工程案例进行方法有效性验证。

2 可靠性综合评定

2.1 “异母体”情形下的验前信息预处理

上世纪40年代Shannon提出了信息熵[16]的概念,首次将事件的不确定度进行了理论上的量化处理。变量离散形式下信息熵的定义为

(5)

式中：x为事件X的可能取值结果；χ为所有结果组成的集合。进一步,给出条件熵的定义如下:

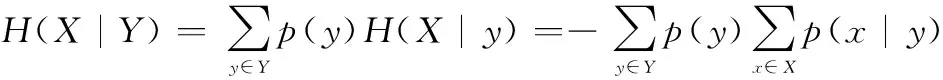
log2p(x|y)

(6)

式中:H(X|Y)表示已知Y的情况下X的不确定度。

可见,信息熵以定量化的手段描述了信息的不确定度,条件熵描述了在已知某种信息情形下该信息的剩余不确定度[17-18]。

基于上述思想,可考虑以信息熵和条件熵模型对无历史样本下可靠度R的不确定性和有历史样本下可靠度R的不确定性进行量化,两种不确定度的差值即为引入历史样本后对消除可靠度R不确定性的贡献值,贡献值占原不确定值的比例越大,说明该历史样本向现场样本的可靠性特征越接近,即相似系数越高。具体方法如下:

(1)无历史样本时,在获得现场样本X=(n*,x*)(其中n*为试验数,x*为成功数)后,条件熵即为可靠性参数R自身的信息熵

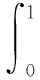
(7)

式中：π0(R|X)为可靠度R的后验概率密度函数。

对于试验结果服从二项分布的弹药装备来说,在无任何先验信息下,可用(0,1)上的均匀分布作为可靠度R的先验分布

则样本X与参数R的联合分布h(X,R)为

进一步求解样本X的边际分布

最后得到R的后验分布,即

(8)

式(8)刚好是参数为x+1和n-x+1的贝塔分布,记为β(x+1,n-x+1)。

将式(8)代入式(7)即可得到可靠度R的信息熵H0(R),具体表达式如下:

(2)引入某类历史样本Xi=(ni,xi)时,可设弹药可靠度R的先验分布为其共轭先验分布β(a,b)。在贝叶斯统计中,如果后验分布与先验分布具有相同的函数形式,则先验分布被称为共轭先验分布[19]。其优点在于代数上的方便性,可以直接获得后验分布的封闭形式,否则只能数值计算。目前常见的一些分布都已通过证明获得其共轭先验分布,如二项分布中以“成功概率”为参数的共轭先验分布为贝塔分布,泊松分布中以“均值”为参数的共轭先验分布为伽马分布。

关于贝塔分布β(a,b)中超参数a,b的确定可基于先验矩方法,过程为:将基于历史数据获得的关于可靠度R的若干估计值记为θ1,θ2,…,θk,由此可计算前两阶先验矩μ1和μ2:

然后令其分别等于贝塔分布的一、二阶矩,即可求解获得超参数a,b的值。

基于现场样本X=(n*,x*)易推导得到后验分布为

πi(R|(X,Xi))=β(a+x*,b+n*-x*)

则条件熵Hi(R)的求解公式为

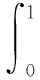
(9)

式中:Hi(R)表示第i类历史样本存在下可靠度R的不确定值,具体表达式为

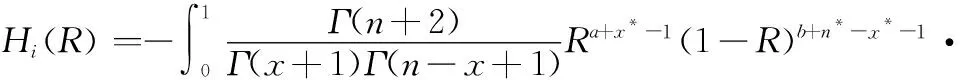
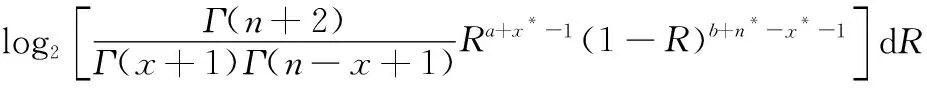
(3)由于获得了第i个来源的验前信息而使参数R的信息熵的损失比为

(10)

显然,KΔHi(R)越大,表示第i个来源的验前信息对消除可靠度R的不确定性所作的贡献越大。

(4)对KΔHi(R)进行归一化处理,作为继承因子值ρi:

(11)

式中:N表示历史样本的类别总数。

上述过程将多源先验信息纳入统一框架,为构建可靠度R的贝叶斯多源混合先验函数奠定了基础。

2.2 可靠性特征量的贝叶斯统计推断

弹药在可靠性鉴定过程中,外场飞行试验结果为“成功”和“失败”两种,服从二项分布[20]。对于二项分布,当随机变量为成功概率(即可靠度R)时,其共轭先验分布为贝塔分布。β(a,b)分布的概率密度函数为

(12)

式中:R为随机变量;a和b为超参数。可基于先验矩方法求解超参数,在此不再赘述。

利用贝叶斯理论进行统计推断的前提是样本来源于同一总体,因此式(12)无法直接作为本文弹药可靠度R的先验分布函数。第2.1节继承因子ρ的确定解决了历史样本与现场样本“异总体”的量化描述问题,因此可构造基于贝塔分布和继承因子ρ的多源加权混合先验分布函数:

(13)

式中:N为历史样本类别数。

样本X和参数R的联合分布为

h(X,R)=p(X|R)π(R)

(14)

式(14)将总体信息、样本信息和先验信息3种可用的信息都综合在了一起。

将h(X,R)作如下分解:

h(X,R)=π(R|X)m(X)

式中:m(X)为X的边际密度函数,即

可见能用来对R作出推断的仅仅是条件分布π(R|X),其求解公式为

(15)

在样本X给定下,式(15)即为R的后验分布的概率密度函数形式。

对于弹药可靠性评估,工程界一般较为关注可靠度置信下限。给定单侧置信度C,可靠度R的置信下限可通过如下公式进行求解:

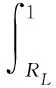
(16)

由此,完成了对高价值弹药的可靠性综合评定。

3 工程案例

某改型高价值弹药,研制总要求中对其可靠性指标规定为:可靠度单侧置信下限不小于0.9。已知定型试验前,收集的有效先验信息如表1所示,除去两个新研电子部件,其余都为沿用该基型弹药的成熟产品。两个新研部件在工程样机鉴定阶段中开展了模拟外场飞行的地面可靠性鉴定试验,成败型数据由计量型数据转换而得。现需要据此制定该型待鉴定弹药在定型阶段的可靠性考核方案。

表1 先验数据

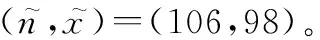
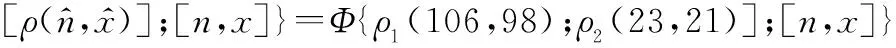
以现场样本为[n,x]=[10,10]为例,基于第2.1节方法可得到历史样本1和2的继承因子值分别为0.43和0.57。基于继承因子和贝塔分布构建混合先验分布函数,其函数图像如图1所示,同时给出了分别基于两类历史样本的单先验分布图。不难发现,混合先验分布是对两类历史样本分别对应先验分布的合理融合,比较符合工程实际。基于2.2节方法推导求解可靠度R的后验分布函数,对应函数图像如图2所示,基于该后验分布即可完成对可靠度等参数的求解计算。

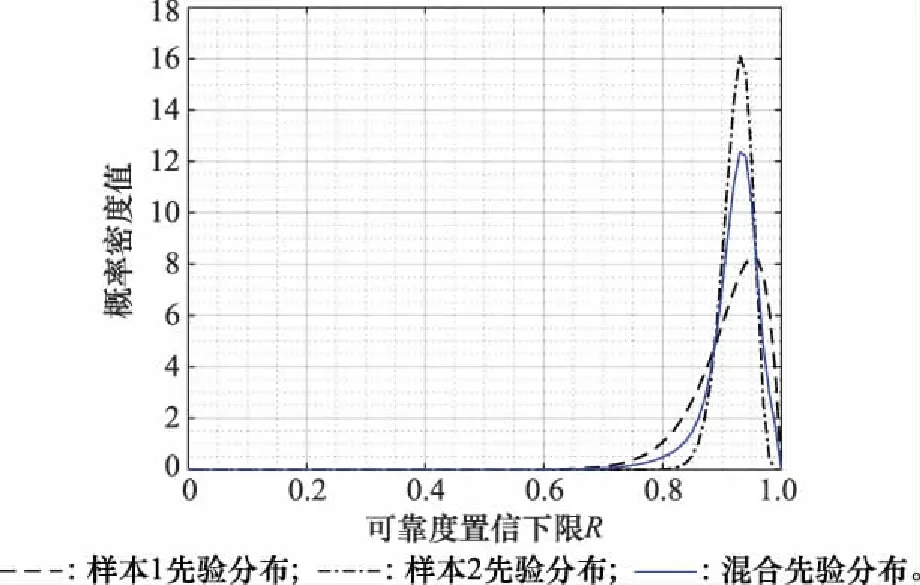
图1 可靠度R的混合先验分布

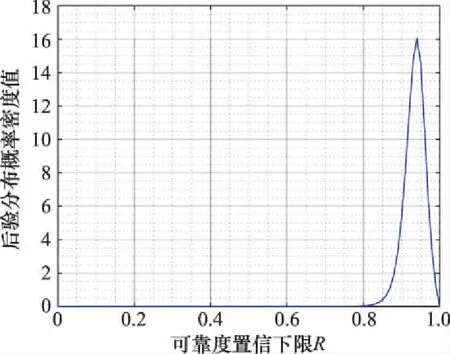
图2 可靠度R的后验分布

目前弹药装备定型阶段的可靠性评估方法主要依据GB/T 4087—2009《数据的统计处理和解释 二项分布可靠度单侧置信下限》,可靠度单侧置信下限的计算公式如下:

(17)

式中:RL为可靠度单侧置信下限;n为样本总数;f为失败数;γ为置信度。

图3给出了基于本文方法分别在0失效和1失效情形下,该型弹药可靠度置信下限随用弹量的变化曲线。同时给出了基于式(16)的传统可靠性评估方法下的可靠度随用弹量变化曲线。可见,传统方法在0失效和1失效下靶试用弹量至少分别为22发和38发才能达到0.9的可靠度,而引入有效先验数据后基于本文方法在评估精度不变的情况下只分别需要13发和25发的靶试量,用弹量分别降低了41%和34%。

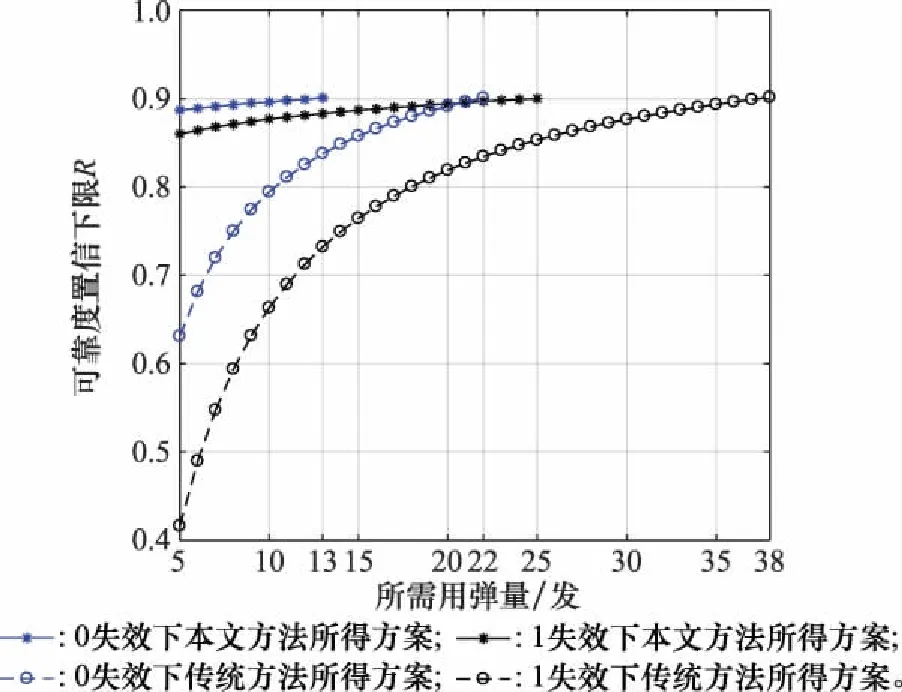
图3 本文方法与传统方法结果对比

4 结 论

针对高价值弹药在可靠性评估中高可靠度、置信度与高用弹量之间的冲突问题,综合利用变动统计理论、信息熵与条件熵理论及贝叶斯理论,建立了适用于弹药装备的小子样可靠性综合评定方法。以某型高价值弹药为应用对象,对本文方法的应用过程进行了说明,给出了该型弹药在高可靠度、高置信度指标要求下的合理用弹量方案,进一步验证了该方法的合理性和可行性。本文方法可直接应用于失效服从二项分布的高价值装备可靠性综合评估中,而对于服从指数分布、正态分布等其他分布类型的可靠性数据,有待进一步研究给出基于小子样变动统计的可靠性评估方法。本文方法可扩展至武器装备的小子样测试性综合评定领域。