晏兵川，李宝毅，张永康

（天津师范大学数学科学学院，天津300387）

1 引言和主要结果

弱化Hilbert第16问题一直是常微分方程定性理论的热门课题之一[1-2].Bogdanov-Takens系统（B-T系统）是向量场的分岔理论研究中一类重要的近Hamilton系统.文献[3-10]研究了在二、三、四次多项式扰动下B-T系统的极限环个数.令Mk（h）为扰动系统的k阶Melnikov函数.对于B-T系统的n次多项式扰动，文献[11]证明了当M1（h）≢0时，极限环个数的上确界为n-1（计重数）;文献[12]证明了当M1（h）≡0，M2（h）≢0时，极限环个数的上确界为（计重数）;文献[13]证明了当Mi（h）≡0（i=1，2，…，k-1），Mk（h）≢0时（k≥3），极限环的个数不超过k（n-1）-1（计重数）.

随着分岔理论的发展，一些研究开始关注分段光滑向量场的定性分析.文献[14]将平面分为上下2个区域，证明了在分段n次多项式扰动下B-T系统的极限环个数不超过12n+6（计重数）.文献[15]将平面分为左右2个区域，证明了在非连续（连续）分段n次多项式扰动下B-T系统的极限环个数不超过16n+计重数）.文献[16]证明了将平面等分成3个扇形区域时，一类分段线性Hamilton系统在n次多项式扰动下至少可以产生2n+（计重数）个极限环.文献[17]证明了一类平面抛物-椭圆型分段光滑线性Hamilton系统在n次多项式扰动下极限环的个数不超过（计重数）.

本文将平面分为上下2个区域，通过计算一阶Melnikov函数，估计非连续分段n次多项式扰动的B-T系统

的极限环个数，其中：0<ε≪1，n∈N+，

当ε=0时，未扰动系统（1）0的Hamilton函数为

设Γh与x轴正半轴和负半轴分别交于点Bh（b（h），0）和Ah（a（h），0）.

本文的主要结果为：

定理 在非连续分段n次多项式扰动下，当h∈一阶Melnikov函数M（1h）≢0时，扰动系统（1）ε的极限环个数不超过

2 一阶Melnikov函数

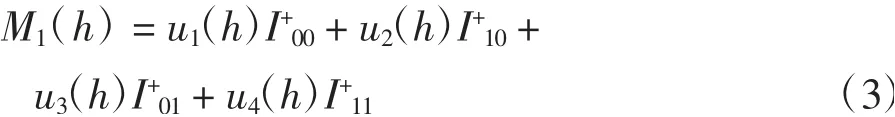
其中：u1（h）、u2（h）、u3（h）、u4（h）为h的多项式，且

证明 由Γh关于x轴的对称性可得

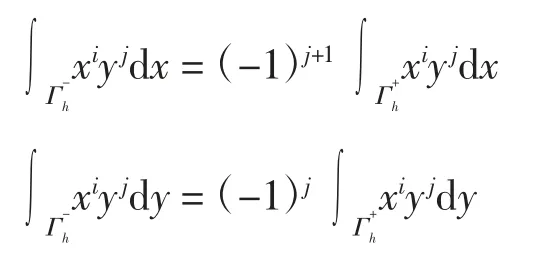
因此

则有

下面只需证明对i+j=n，I+ij满足

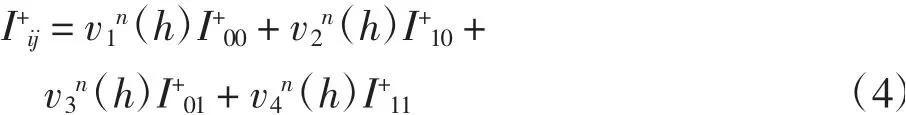
其中：v1n（h）、v2n（h）、v3n（h）、v4n（h）为h的多项式，且

对式（2）关于x求导得

式（5）两端同乘以xi-2y jdx（i≥2），并沿Γ+h积分得

当i=2时，有

即

当i≥3时，由式（6）可得

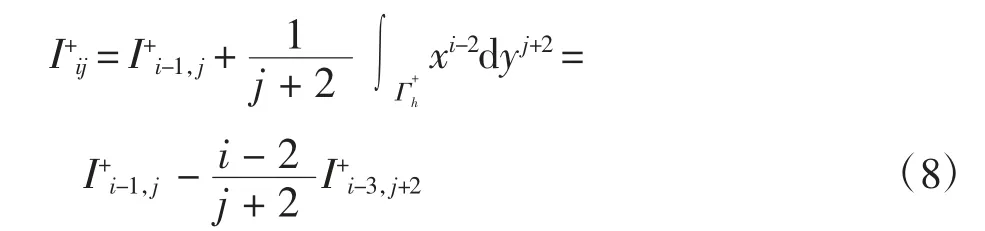
式（2）两端同乘以xiy j-2dx（j≥2），并沿Γ+h积分得

即

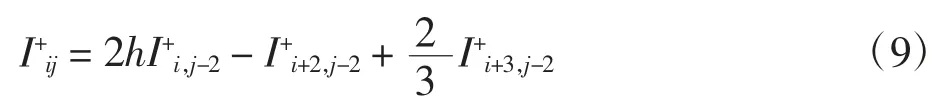
由式（8）～式（9）可得

在式（7）和式（10）中分别取j=0和（i，j）=（0，2），可得

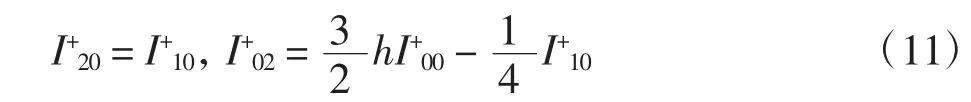
在式（8）和式（7）中分别取（i，j）=（3，0）和j=1，可得

在式（10）中取（i，j）=（1，2）、（0，3），可得

下面对n使用数学归纳法证明式（4）成立.由式（11）～式（13）可知式（4）对n=0、1、2、3成立.假设当n=i+j≤k-1（k≥4）时式（4）成立，则当n=k，即i+j=k时，在式（10）中取（i，j）=（0，k）、（1，k-1），在式（7）中取j=k-2，在式（8）中取（i，j）=（l，k-l）（3≤l≤k），可得

由归纳假设，当n=k时，I+ij有形如式（4）的表达式.下面利用式（14）估计多项式v1n（h）、v2n（h）、v3n（h）、v4n（h）的次数.

情形1 当（i，j）=（0，k）、（1，k-1）时，有

因此可得

情形2 当（i，j）=（2，k-2）时，I+2，k-2=I+1，k-2，此时显然有

情形3 当（i，j）=（l，k-l）（3≤l≤k）时，有

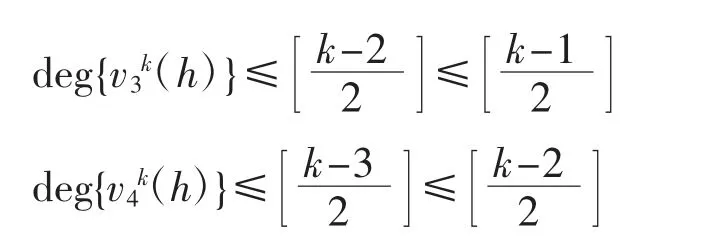
综上可得式（4）成立.引理1证毕.

引理2I+00、I+′00在上无零点.

证明 将Ah（a（h），0）和Bh（b（h），0）代入式（2）得

则有

因为a（h）≠b（h）且a（h）+b（h）<1，故I+′00≠0.引理2证毕.

记Δ（h）=h（6h-1）.

引理3I+00、I+10满足Picard-Fuchs方程组

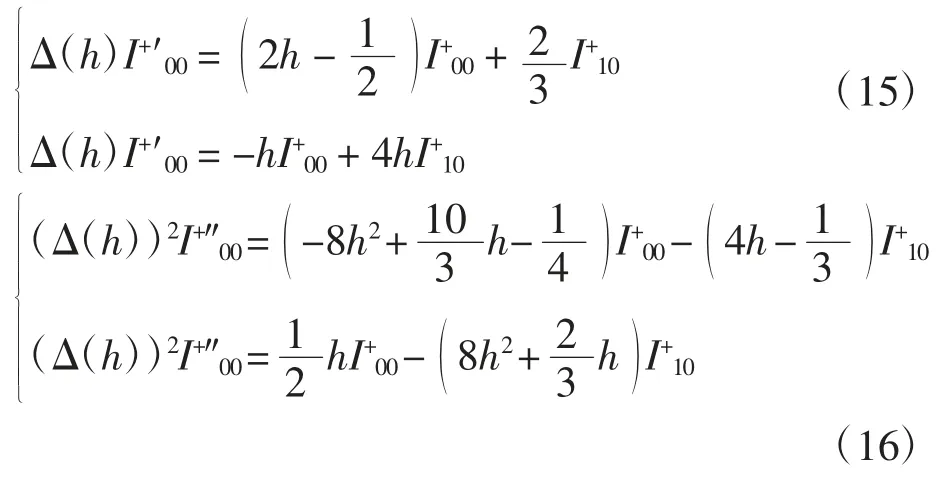
证明 考虑积分

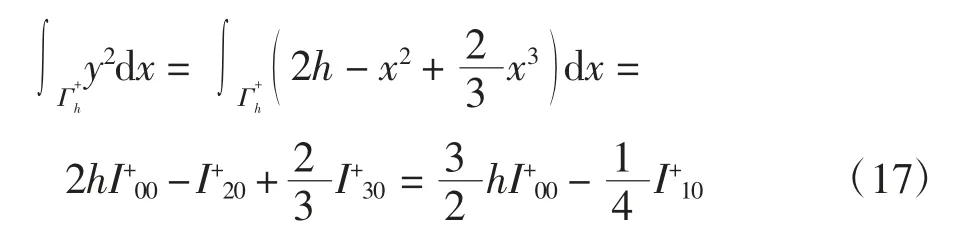
注意到

因此对式（17）关于h求导可得

整理得

考虑积分

注意到

因此，对式（19）关于h求导可得

整理得

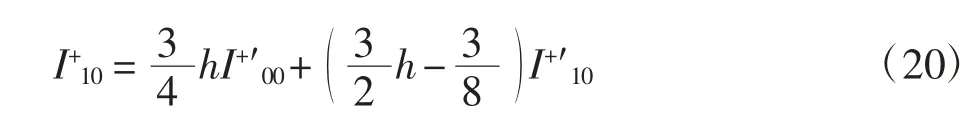
联立式（18）和式（20）可得

因此式（15）成立.对式（15）关于h求导，经整理可得式（16）.引理3证毕.

利用

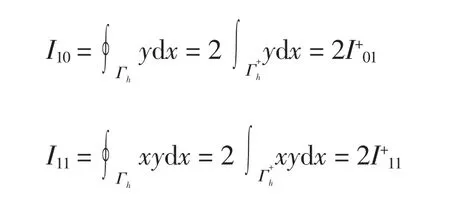
并结合文献[18]的推论1*可得引理4.

引理4I+01、I+11满足Picard-Fuchs方程组

3 极限环个数的估计

命题1[19]设系统满足

（1）P（h）在闭区间[a，b]上连续，在开区间（a，b）内可导；

（2）A（h）和B（h）在闭区间[a，b]上连续，F（h，P）在[a，b]×[mp，Mp]上连续，其中[mp，Mp]为F（h，P）在[a，b]上的值域.

则有以下结论：若A（h）和B（h）在开区间（a，b）内分别有个和个零点（，计重数），则函数P（h）在开区间（a，b）内至多有个零点（计重数）.

命题2[15]P2（h）、P1（h）、P0（h）和R（h）为开区间K上的充分光滑的连续函数，P2（h）的零点是孤立的，且

存在非平凡解Φ1（h），则

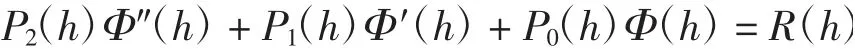
的任一解在K上的零点个数（计重数）不超过p+2w+r+2，其中p、w、r分别为P2（h）、Φ1（h）、R（h）在K上的零点个数（计重数）.

定理的证明 （f h）在上的孤立零点个数记为#f（h）（计重数）.

当n=1时，系统（1）ε的一阶Melnikov函数为

其中：u1、u2、u3为常数.令φ1（h）=I+01，定义二阶微分算子（其中I为恒同算子），由式（22）可知L1（φ1（h））≡0，将式（18）和式（20）代入式（16）可得

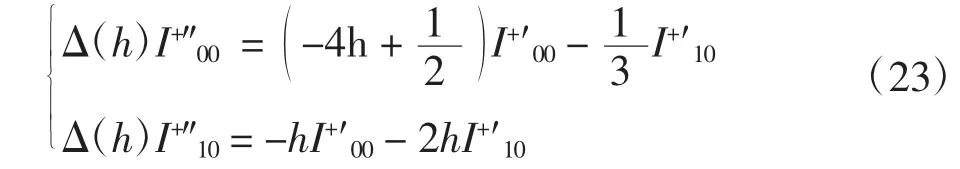
则有

其中：

由式（23）可得

令G（h）=α11（h）+α12（h）w（h），则有

其中：

所以#B1（h）≤3，由命题1可知

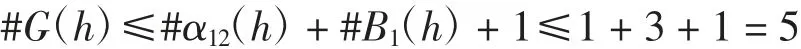
再由命题2可得

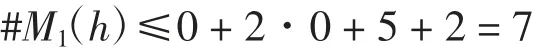
即当M1（h）≢0时，系统（1）ε至多存在7个极限环.

当n≥2时，在式（3）中令

对ψ2（h）关于h求导，由引理4可得

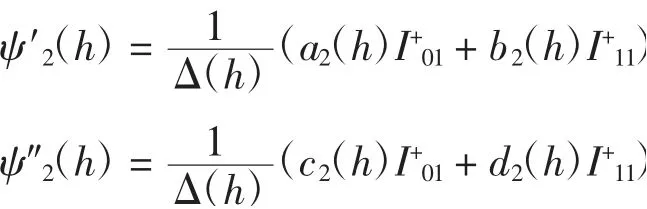
其中：

从而

事实上，设P1（h）为k次多项式，P2（h）和P0（h）均为k+1次多项式，则式（24）左端为关于h的次数不超过β+k+1的多项式，共有β+k+2项，令其各项系数为0，得到β+k+2个线性方程.式（25）左端为关于h的次数不超过α+k的多项式，共有α+k+1项，令其各项系数为0，得到α+k+1个线性方程.因此可得到一个含有α+β+2k+3个方程的线性方程组.

又由于P1（h）中有k+1个待定系数，P2（h）和P0（h）中分别有k+2个待定系数，则线性方程组共有3k+5个待定系数，因此当3k+5>α+β+2k+3，即k>α+β-2时，线性方程组存在非零解.取k=α+β-1，则存在系数不全为0的实系数α+β-1次多项式P1（h），α+β次多项式P2（h）和P0（h），使得L（ψ2（h））≡0.

对ψ1（h）关于h求导，结合式（18）、式（20）和式（23）可得

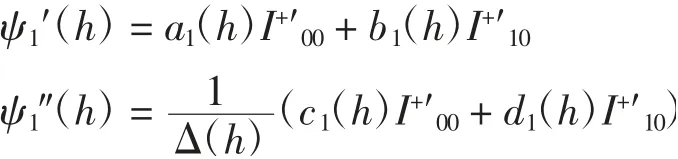
其中：

从而

因此

其中：

从而

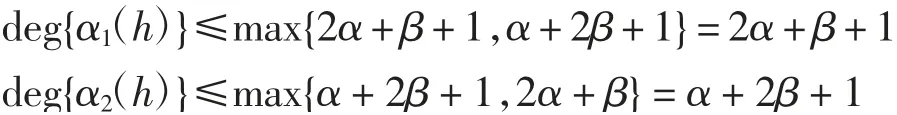
令G（h）=α1（h）+α2（h）w（h），则有

其中：

则有

因此，由命题1可知

由P2（h）的多项式次数可得

根据Petrov定理[20]可知w=#ψ2（h）≤α+β，再由命题2可得

取n=1，有因此当M（1h）≢0时，扰动系统（1）ε的极限环个数不超过计重数）.定理证毕.