郭春晓，郭艳凤

（1.中国矿业大学（北京）理学院，北京 100083；2.广西科技大学 理学院，广西 柳州 545006；3.中国地质大学（武汉）数理学院，湖北 武汉 430074）

0 引言

在数学物理、大气海洋和其他应用科学的各个分支中，存在着许多由非线性偏微分方程描述的混沌现象。某些非线性偏微分方程精确解的表达形式对解释相应的混沌现象具有重要意义。到目前为止，已经有一些有效方法可得到具体的精确解形式，例如Painleve分析法［1］、back lund变换法［2-3］、Hirota双线性变换法［4］、逆散射法［5］、tanhcoth方法［6-7］、G′／G展开法［8-9］、扩展的双Darboux变换法［10］等。然而，这些方法在应用中有着不同的限制条件，一般情况下没有一个通用方法可以求解所有的非线性偏微分方程。通过改进辅助的常微分方程和相应的待定函数的表示形式推广和改进G′／G方法［11］，即扩展的G′／G展开法，可以得到更多的精确解形式。本文主要利用扩展的G′／G展开法讨论广义KdV-mKdV方程的精确解形式。

广义KdV-mKdV方程［12］为

其中，α，β，γ，ε为实数。这个方程是物理学许多分支中重要的一类模型，描述了一维非线性晶格中部分有界波在简谐力作用下的传播，特别描述了等离子体物理中无Landau阻尼的小振幅离子声波的传播，它也被用来解释固体物理中热量通过氟化钠单晶的传播。近年来许多研究者对其进行了研究［12-15］，并得到了丰富的精确行波解，包括双周期Jacobi椭圆函数解。在极限情况下，这些解退化为相应的孤立波解和激波解。本文主要用扩展的G′／G展开法研究广义KdV-mKdV方程的混沌现象，并得到了一些新的精确解。

1 预备知识

通常情况下，以常微分方程

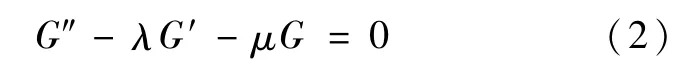
为基础，其中，λ和μ为任意常数。利用G′／G展开法研究某些偏微分方程，得到了具有u（ξ）＝的行波解形式，其中aN≠0，见文献［8］。进一步地，行波解的表达式可以延伸为u（ξ）＝，其中a－N和aN至少一个不为0。

近年来，某些学者通过线性常微分方程（2）引入了一种求非线性偏微分方程更多新解的有效方法，即假设解具有形式u（ξ），其中a－N和aN至少一个不为0［8，11］。在此基础上，再利用新的非线性常微分方程作为辅助方程，构造了一些非线性偏微分方程更丰富的解［11］，该方法可以看作是原展开法的推广。

这个新的非线性常微分方程可以写成

其中，A，B，C，E为待定参数。令G′／G＝H（ξ），当这些参数满足不同条件时，可以得到非线性常微分方程（3）具体解的表达形式，参见文献［11］。

记M＝A－C，Ω＝B2＋4EM，Δ＝EM，

根据H（ξ）在不同条件下的表达形式，通过扩展的G′／G展开方法可以得到更多广义KdVmKdV方程新的精确解形式。

2 广义KdV-mKdV方程的精确解

式（1）中，γ＝1时，广义KdV-mKdV方程为

进一步地，式（10）两边关于ξ积分可得

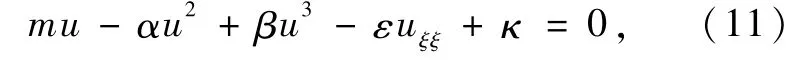
其中，κ为积分常数。对非线性方程（11）中的最高阶导数项uξξ和最高阶非线性项u3运用齐次平衡法，待定表达式u（ξ）＝中的最高次数N满足等式N＋2＝3N，解可得N＝1。

令H（ξ）＝G′／G，假设方程（11）具有如下形式的解，

其中，a0，a1，a2，d为待定参数。将式（3）和（12）代入式（11），通过Maple软件进行计算，方程可以转换成关于（d＋H（ξ））N（N＝0，±1，±2，…）的多项式。进一步令d＋H（ξ）的不同次数幂的系数为0，可以得到包含相关参数的代数方程组。通过Maple软件求解这些代数方程组，可以得到如下参数之间的关系。

情形1当A≠0，βε＞0时，

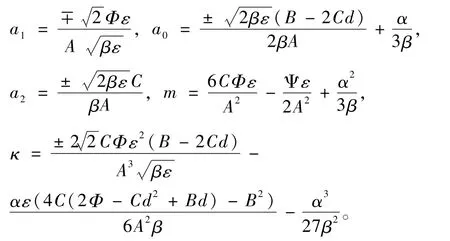
此种情况下，将上面参数关系式代入式（12）中，可得如下新精确解的表达形式

其中，ξ＝x－mt，H（ξ）分别满足式（4）～（8），Φ＝－Cd2＋Bd＋A－E，Ψ＝B2＋4C（A－E）。当参数满足式（4）～（8）的条件和关系时，上述解即为新精确解形式。

情形2当A≠0，βε＞0，C≠0，d＝B

2C≠0时，

此种情况下，将上面参数关系式代入式（12）中，可得如下新精确解的表达形式

其中，ξ＝x－mt，H（ξ）分别满足式（4）～（8），Φ＝－Cd2＋Bd＋A－E，Ψ＝B2＋4C（A－E）。当参数满足式（4）～（8）的条件和关系时，上述解即为新精确解形式。

特别地，在情形2中，当C≠0，时，所得到的解是用扩展的展开法得到的新精确解中的特例，可明显看到新解形式中d可以取不为0的值。

情形3当a2＝0，A≠0，C≠0，βε＞0，B－2Cd≠0，Φ≠0，α－3βa0≠0时，有

此种情况下，将上述关系式代入式（12），得到如下新的精确解表达形式

其中，ξ＝x－mt，H（ξ）分别满足式（4）～（8），Ψ＝B2＋4C（A－E），a1由上面的关系式决定。

特别地，当α－3βa0＞0，A＞0时，参数关系式可简化为

3 结果分析

根据情形1中解的5种情况图形分析解的主要结构和性质。情形1中，如果可以得到如下具体解的形式。

当B≠0，Ω＞0时，取

于是有

利用Map le可以得到解u11的图形，如图1所示。从图1可以看出，短时间内，广义KdV-mKdV的孤波解主要出现在小的窄区域内，可能会发生怪波的突变情况。从解的表达形式看，当分母趋于0时，会出现爆破现象。

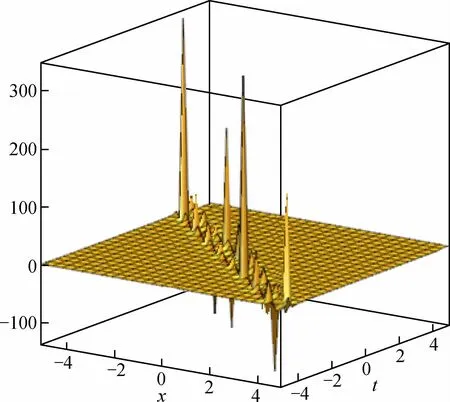
图1 B≠0，Ω ＞0时u11的图形Fig.1 Solution u11 when B≠0，Ω ＞0

类似地，当自由参数为不同条件下的值时，都可以得到相应解的具体形式。下文只给出相应的参数取值情况，并描述相关图形。

当B≠0，Ω＜0时，取

ε＝β＝－1，A＝2，α＝B＝C＝E＝d＝C2＝1，Ω＝B2＋4E（A－C）＝－3＜0，C1＝利用Map le可以得到解u12的图形，如图2所示。从图2可以看出，较短时间内，广义KdV-mKdV mKdV的周期解出现在比较大的区域内。破坏特性在一定时期内可能是渐近的、周期性的。而爆炸现象的出现和情形1原因相同。

图2 B≠0，Ω ＜0时u12的图形Fig.2 Solution u12 when B≠0，Ω ＜0

当B≠0，Ω＝0时，取ε＝β＝－1，B＝C＝2，α＝A＝E＝C2＝1，d＝C1解u13的图形参见图3。从图3可以看出，短时间内，广义KdV-mKdV的有理解在小区域内出现，怪波的破坏性发生很明显，并且在整个区域内以对称形式不断发生，引起爆破现象。

图3 B≠0，Ω＝0时u13的图形Fig.3 Solution u13 when B≠0，Ω＝0

当B＝0，Δ＝E（A－C）＞0时，取ε＝β＝－1，A＝2，α＝C＝E＝C2＝1，d＝C1解u14的图形见图4。在此条件下，给出了广义KdVmKdV在小区域内的孤立波解，破坏性逐渐缓慢发生，与前面的爆破现象有所不同。

图4 B＝0，Δ ＞0时u14的图形Fig.4 Solution u14 when B＝0，Δ ＞0

当B＝0，Δ＝E（A－C）＜0时，取ε＝β＝－1，A＝－2，α＝C＝E＝C2＝1，d＝C1解u15的图形见图5。广义KdV-mKdV在区域内出现周期解的形式，破坏特性渐近出现，并具有一定的周期性。

图5 B＝0，Δ ＜0时u15的图形Fig.5 Solution u15 when B＝0，Δ ＜0

同样，其他情况下自由参数给定后，根据参数之间的关系可以得到相应解的图形和性质，本文不再赘述。从这些新精确解的性质看，都具有一定的爆破现象，从而在自然现象中特殊条件下怪波现象的出现是有一定条件的。这些解的形式对理解自然界中的怪波现象具有重要意义。

4 结语

本文通过扩展的G′／G展开法，得到了一类广义KdV-mKdV方程新的精确解形式。情形1中当C＝0时，方程（3）化为方程（2），得到通常意义下G′／G展开法所用到的线性常微分方程解的形式。而当C≠0，d≠0时，可以借助非线性常微分方程得到扩展的G′／G展开方法中的待定解形式。用扩展的G′／G展开方法所得到的解在特殊情况下包含了一般情形下的解，除此之外还得到了一些新精确解的表达形式，并解释了部分怪波的形成机理。理论和实际计算表明，扩展的G′／G展开方法在研究非线性偏微分方程的新精确解和怪波现象方面具有重要意义。

当α＝0或β＝0时，可以将KdV-mKdV方程分别转化为mKdV方程或KdV方程。根据上述解的表达形式，当β→0时，选取一些适当的参数值，可以进一步考虑mKdV方程新的精确解形式。这种计算方法可以应用于求解更多非线性系统的一些新精确解形式，具有一定推广性。