Chang-Yao Liao and Xian-Ting Liang

Department of Physics,Ningbo University,Ningbo 315211,China

Abstract In this paper,we derive the Lindblad and Redfield forms of the master equation based on the Born–Markov master equation with and without the secular approximation for open multi-level quantum systems.The coefficients of the equations are re-evaluated according to the scheme in[(2019),Phys.Rev.A 99,022118].They are complex numbers rather than the real numbers obtained from traditional simplified methods.The dynamics of two models(one is an open threelevel quantum system model,and the other is the model of phycoerythrin 545 (PE545) in a photosynthesis system)are studied.It is shown that the secular approximation and the simplified real coefficients may cause a small distortion of the dynamics in some environments,but a large distortion of the dynamics in others.These effects are discussed and characterized by studying the dynamics of nontrivial instances of multi-level systems in the presence of dissipation.

Keywords: Master equation,secular approximation,Redfield form,Lindblad form

1.Introduction

It is known that no real physical systems exist in complete isolation in nature.They unavoidably suffer from interactions with uncountable degrees of freedom in their surroundings,and the evolution of their quantum states is affected by this kind of interaction.Thus,understanding the dissipative quantum dynamics of a system embedded in a complex environment is an important topic across various sub-disciplines of matter science [1–10].In the study of reduced quantum dissipative dynamics,it is extremely convenient to use the Lindblad and Redfield forms [11–13] based on the Born–Markov master equation.The general Lindblad and Redfield equations can be derived using the secular approximation and they are widely applied in investigations of the evolution of the reduced density matrix of the interesting quantum systems [14–21].However,some investigations show that the secular approximation may distort the actual dynamics of the quantum systems under investigation[22].In recent years,many non-secular Lindblad and Redfield forms of the master equation have been derived for some specific models,and many interesting results have been obtained based on these forms [23,24].However,it would be convenient to formulate the master equation into the Lindblad and Redfield forms without secular approximation for the general physical model.Recently,there has been some progress in this field[22,25–27].Schaller et al[27]proposed a coarse-grained approach with a dynamically adapted coarsegrained timescale.In this method,the secular approximation is not used and the positivity of the reduced dissipative dynamics is preserved.Lidar et al [22] also obtained the Markovian master equation without invoking the secular approximation through a coarse-grained time treatment.In this coarse-grained approximation,a Lindblad master equation is proposed.By optimizing the coarse-grained timescale,this approach can predict the dissipative dynamics of some open quantum systems.Several models have been investigated using this method.It has been shown that the secular approximation has a nontrivial effect on the dynamics of the populations,and that the master equation derived from the secular approximation misses some features of the dynamics.

However,although this approach saves the positivity of the dynamics and gives up the secular approximation,the coarse-grained approximation should be used instead.In section 2,we will derive the Lindblad and Redfield master equations based on the Born–Markov master equation without using any other approximations.The non-secular equations that we obtain can be used as easily as the traditional forms.For convenience,we call the corresponding equations with and without use of the secular approximation the secular and non-secular Lindblad and Redfield master equations.As will be seen,the non-secular Lindblad and Redfield equations obtained immediately degenerate to the traditional secular Lindblad and Redfield equations when we add the secular approximation to them.It can easily be seen that the non-secular Lindblad and Redfield equations include many more terms;however,some of them are discarded in the secular Lindblad and Redfield equations because they do not satisfy the criterion of secular approximation.

Another possible factor that affects the accuracy of the master equations is when the imaginary parts of the equations’ coefficients are ignored.According to Redfield’s original paper [11],in order to determine the equations’coefficients exactly,a Cauchy principle value integral should be solved,for which it is always difficult to obtain the analytic form of the integral[28].Therefore,the imaginary part of the spectral correlation tensor is always ignored,which may also result in distortion of the true reduced dynamics of open quantum systems.In [29],we proposed a scheme for evaluating the coefficients in the Born–Markov master equation.It is interesting that the scheme can also be used to exactly evaluate the coefficients of the Lindblad and Redfield equations.In section 3,we will re-evaluate the equations’coefficients according to the method in [29].

In section 4,as examples,we will investigate the dynamics of two models by using the secular and non-secular equations with the traditional real coefficients and our obtained complex coefficients in the equations.One model is a three-level quantum system,and the other is the PE545 complex[30–32],which is a model extensively used to study photosynthetic pigment protein complexes.We will show that the secular approximation and the simplified real coefficients may cause a small distortion of the dynamics in some environments,but a large distortion in other environments.These investigations suggest that when we want to exactly solve the dynamics of some dissipative quantum systems,we should use the non-secular Lindblad and Redfield master equations,and the complex coefficients in the equations.

2.Model and formulation

In this section,we derive the non-secular Lindblad and Redfield equations.As usual,the total system environment Hamiltonian is set to [28,33]

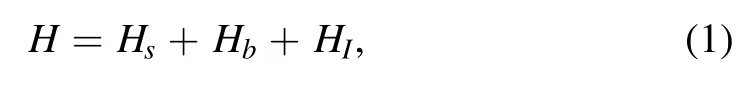
where Hs,Hb,and HIare the Hamiltonian of the system,the bath,and the interaction between the system and its environment.Supposing the interaction Hamiltonian is described by

where Sαand Eαare the system and environment operators,the general Hamiltonian of the open multi-level quantum system can be written as

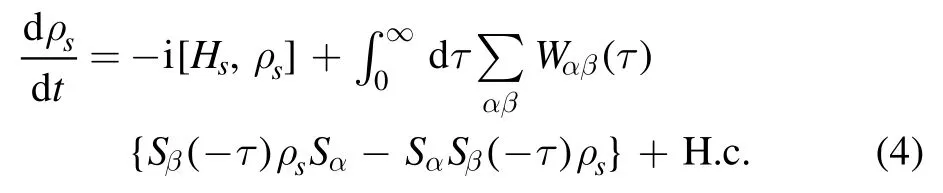
Here and in the following,we set ħ=1,and define

It is not convenient to use equation(4)in a numerical analysis of reduced quantum dissipative dynamics.Fortunately,two computable forms,the Lindblad and Redfield master equations,have been introduced and extensively used in recent years.These equations have been derived in many references.However,in general,these derivations depend on the support of additional approximations.In the following,we re-derive these equations based on the Born–Markov master equation without the help of other approximations and assumptions.

2.1.Lindblad forms

In this section,we derive the Lindblad forms of the master equation with and without the use of the secular approximation.Setting

we can write equation (4) as

Here,Sαis a Hermitian operator,soSα=.Because

where

the Born–Markov master equation can be rearranged into

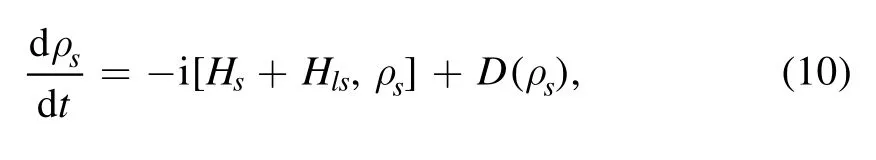
with

and

After some tedious but straightforward calculation (see appendix A),we can obtain

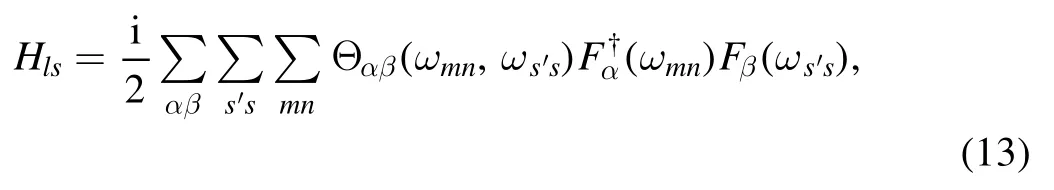
and

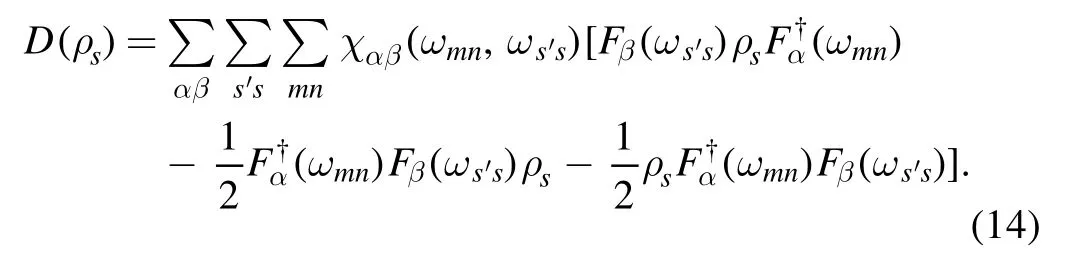
Here,Θαβ(ωmn) and χαβ(ωmn) are defined by equations (53)and (54) in appendix A.Equation (10) together with equations (13) and (14) is the non-secular Lindblad form of the master equation.Furthermore,this form degenerates into the traditional Lindblad master equation when the secular approximation is applied,which means that in these equations,only the termsare included.The equation can now be expressed in the secular form as[37,38]

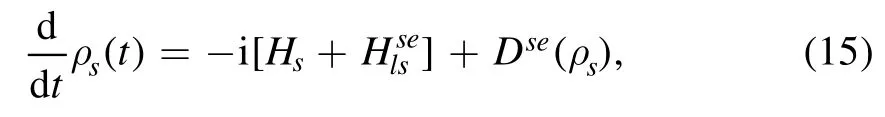
with

and

Thus,we have obtained the Lindblad forms of the master equations with and without secular approximation.

2.2.Redfield forms

Similarly,in the following,we derive the Redfield equations with and without the secular approximation.It is known that in the interaction scenario,we have

From equations (4) and (18),we have

Some simple algebra(see appendix B)results in the Redfield equation in the interaction scenario as

with

Thus,coming back to the Schrödinger scenario,we can obtain the Redfield equation as

with

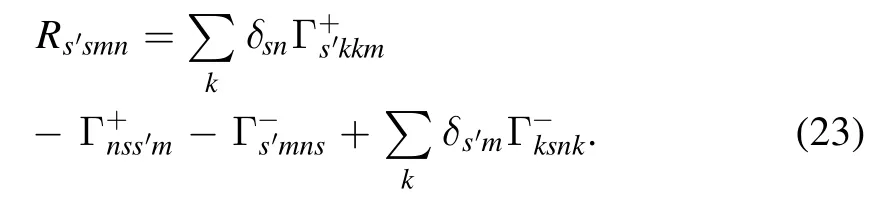
3.On the coefficients in the Lindblad and Redfield master equations

To study quantum dissipative dynamics by solving the Lindblad and Redfield equations(10),(15)and(22),we must know the equations’ coefficientsχ αβ(ωmn,ωs′s) ,Θαβ(ωmn,ωs′s) andwhich depend on ascertaining the spectral correlation tensor Γαβ(Δ) for an identified Δ.In the following,we reevaluate the quality according to the scheme for calculating the coefficients of the Born–Markov master equation given in[29].It is known that when α ≠β,we have Wαβ(τ)=0,and when α=β,we set Wα(τ)=Wαβ(τ).Therefore,the correlation function can be calculated as

where we note that 〈qj(τ)|qk〉=0 for j ≠k,and(ωj)=where kBis the Boltzmann constant,and T is the temperature.Traditionally,from Wαβ(τ),we can obtain the spectral correlation tensor of the bath for an identified Δ as

Due to

where P indicates the Cauchy principal value,and ignoring the imaginary part of the integral,one has

Here,

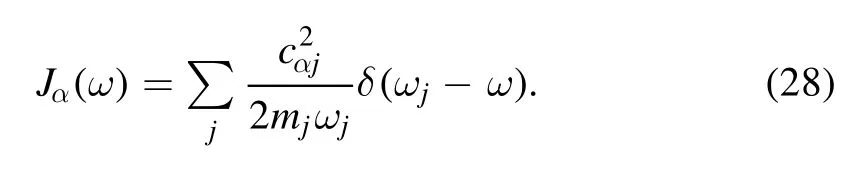
The term Jα(ω) is always described with a environmental spectral density function,for example,the Drude spectral density function [13],as

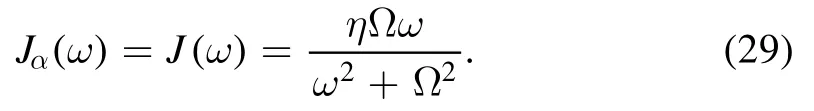
Supposing that the baths to be coupled to all modes of the system are the same,Γαβ(ωmn) can then be obtained as

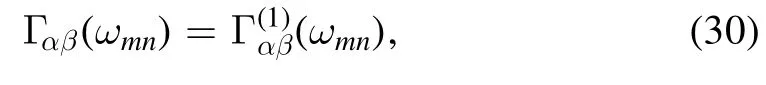
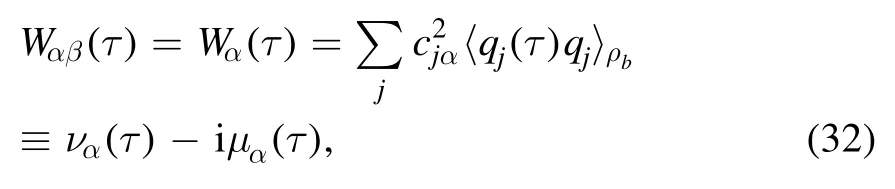
where

Thus,we can recalculate Γαβ(ωmn).When α ≠β,we have Γαβ(ωmn)=0,and when α=β,we have [29]

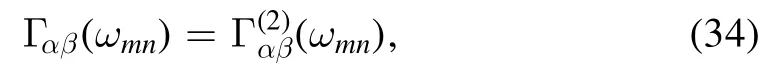
where,

with [29],

4.Two examples

In this section,we investigate the dynamics of an open threelevel quantum system model and the PE545 complex model using the Lindblad and Redfield master equations (10),(15)and (22) withand.

4.1.An open three-level quantum system model

First,we investigate an open three-level quantum system model.In this model,the system’s Hamiltonian is set to

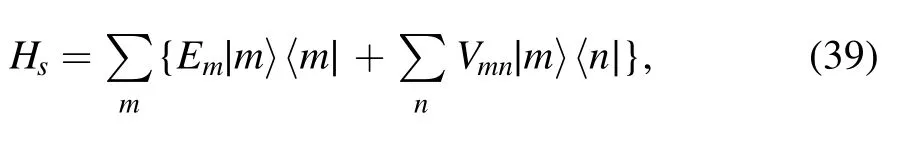
where we assign E1=0,E2=−2.67 cm−1,E3=−3.67 cm−1,and V13=V31=0,V12=V21=V23=V32=0.67 cm−1,and we set the the environmental spectral density function to the Drude form using equation (29).We let η=0.125,Ω=100.0 cm−1,and we set the environmental temperature to 300 K.The initial state is set to ρ(0)=|1〉〈1|.Numerical analysis shows that when N>=100,andare convergent,so we set N=100 in equation (37) in the computation.The reduced dynamics of the open three-level system is solved,and the elements of the reduced density matrix are plotted in figure 1.

However,when the system is embedded in a different environment,the secular approximation and the simplified real coefficients may distort the actual dynamics.For example,suppose the same system is embedded in an environment whose spectral density is still described by the Drude form,and its parameters are unchanged except for η,which changes from 0.125 to 5.0.The elements of the reduced density matrix for the open three-level system are plotted in figure 2.It is shown that in this case,the dynamics of the reduced system is different when we choose different equations (secular versus non-secular equations) or parameters (realor complexIn this environment,the real coefficients,in particular the secular approximation,greatly reduce the timescale of the system’s dynamics.

Similarly,we can take another case whereby in the Drude spectral density function,the parameter Ω changes from 100.0 cm−1to 15.0 cm−1and the other parameters are the same as those used for figure 1.The elements of the reduced density matrix for the open three-level system are plotted in figure 3.It is shown that,in this case,the dynamics of the reduced system is very sensitive to the choice of equations (secular versus non-secular) and parameters (realor complexIn this environment,the real coefficients,especially the timescale of the system dynamics,are greatly reduced when we use the secular approximation.

4.2.The PE545 model

Secondly,we investigate the reduced dynamics of phycoerythrin 545 (PE545) from Rhodomonas CS24 [30,32].The Hamiltonian can be described as

The values of the site energies ∊m(cm1) and the coupling strengths Δmn(cm1) are listed in table 1.

Figure 2.The evolution of the reduced density matrix for a three-level quantum system.The meanings of the symbols and the values of the parameters are the same as in figure 1,except that η=5.0.

Similarly,if we change the environments so that the bath’s parameter η becomes larger,for example,η=100.0,or the bath parameter Ω becomes smaller,for example Ω=100.0 cm−1,the dynamics of the reduced system then becomes very sensitive to the choice of equation (secular or non-secular) and the parameters (realor complexIn this environment,the secular approximation greatly reduces the timescale of the system dynamics,and the real coefficients also seriously affect the reduced dynamics.

From above two examples,we can see that the secular approximation and the use of an inexactmay cause the reduced dynamics of the open system to be slightly distorted in some environments(smaller η and bigger Ω),and they may make the dynamics very distorted in other environments (with bigger η and smaller Ω).Our analysis shows that the two models above are insensitive to the choice of the secular versus the non-secular equation,and the real versus complex parameters when the temperature T is changed in the range T>10 K.However,when the temperature is very low,these master equations based on the Markovian approximation are not very effective,because in this case the non-Markovian effects become very strong.

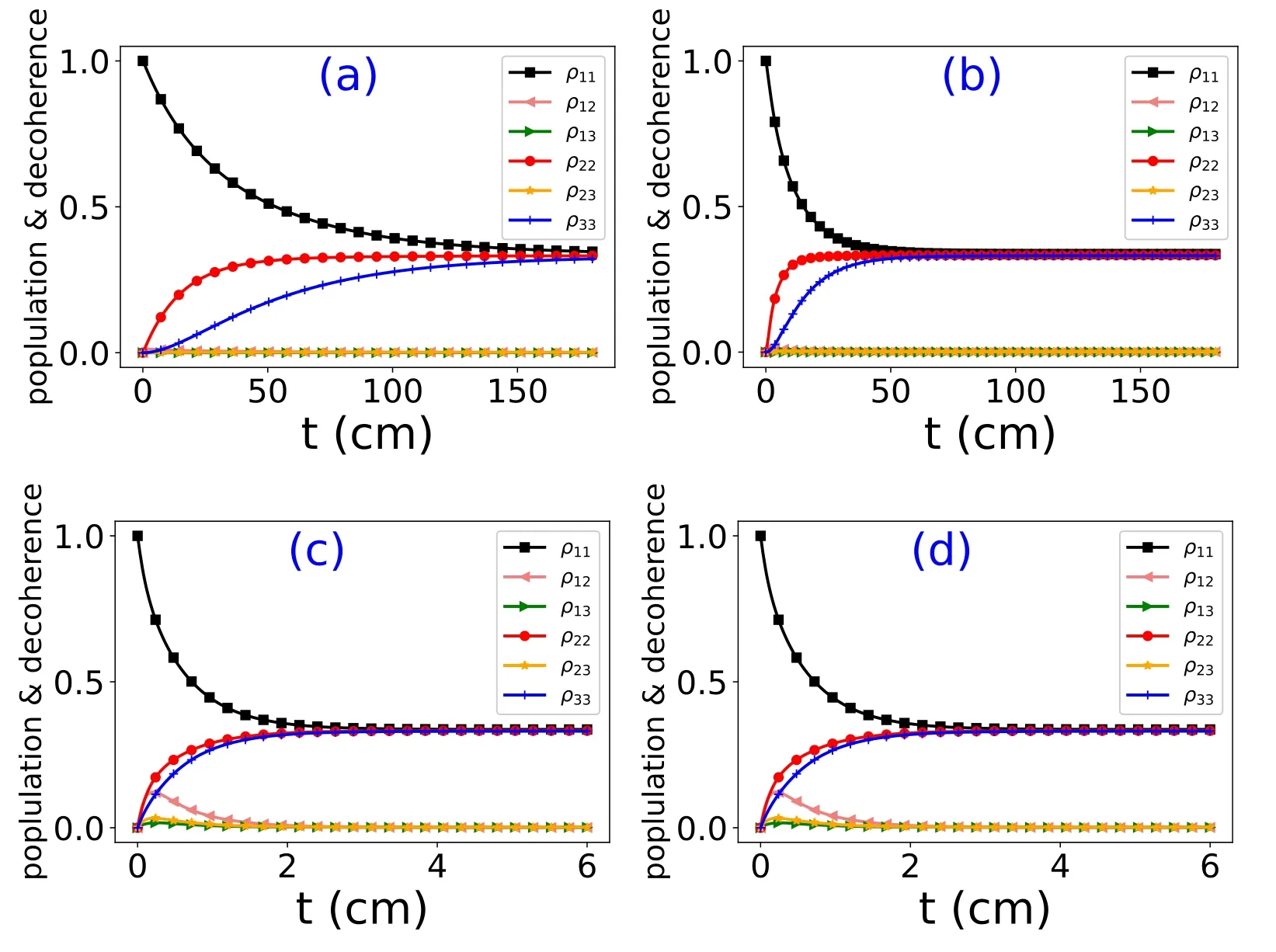
Figure 3.The evolution of the reduced density matrix for a three-level quantum system.The meanings of the symbols and the values of the parameters are the same as those used for figure 1,except that Ω=15.0 cm−1.

Table 1.The values of the site energies ∊m (cm−1) and the coupling strengths Δmn(cm 1) between the sites of PE545.

5.Discussion and conclusions

In this paper,we have re-derived the computable forms of the Lindblad and Redfield equations based on the Born–Markov master equation with and without the secular approximation,and re-evaluated the corresponding coefficients in these equations for multi-level open quantum systems.We investigated two quantum system models using the secular and non-secular forms of the Lindblad and Redfield master equations with different representations of the equations’coefficients derived from the spectral correlation tensorsandOne model was an open three-level quantum system,and the other was the PE545 model.It was shown that the secular approximation and the equations’ real coefficients obtained from the simplified spectral correlation tensormay not seriously affect the accuracy of the dynamic results in some environments,but they may seriously affect the results in other environments.When the temperature is not very low,the results were insensitive to the choice of the secular versus the non-secular equation and the real or complex coefficients.It is worth noting that for the secular Lindblad and Redfield equations,given an input physical state ρin,the output time-evolved state and the steady-state ρoutare always physical.We considered that the positivity of the Born–Markov equation was not assured;however,it was confirmed that for the models investigated and under our chosen conditions,there were no negative populations in the evolution of the reduced density matrix as the dynamics were studied using the non-secular Lindblad and Redfield equations.This means that the dynamics generated using the non-secular Lindblad and Redfield forms may not include non-physical states.However,further theoretical exploration of the problem is needed to reach a general conclusion.

Acknowledgments

This project was sponsored by the National Natural Science Foundation of China (Grant No.21773131),and the K.C.Wong Magna Foundation of Ningbo University.XTL thanks Zi-Hui Liu,Xuan-Chao Zhang,Xuan Leng,Jiong Cheng,and Wen-Zhao Zhang for helpful discussions,and also the referee for many beneficial comments.

Appendix A

We denote the eigenvalues of Hsby ωnand the projection onto the eigenspace belonging to the eigenvalue ωnby ∏(ωn).Then,we define the operators ([28])

Here,ωmn=ωn−ωm.Summing over all energy levels and employing the completeness relation in equation(41),we get

Thus,we have

Inserting the form of equation (43) into equation (6),we obtain

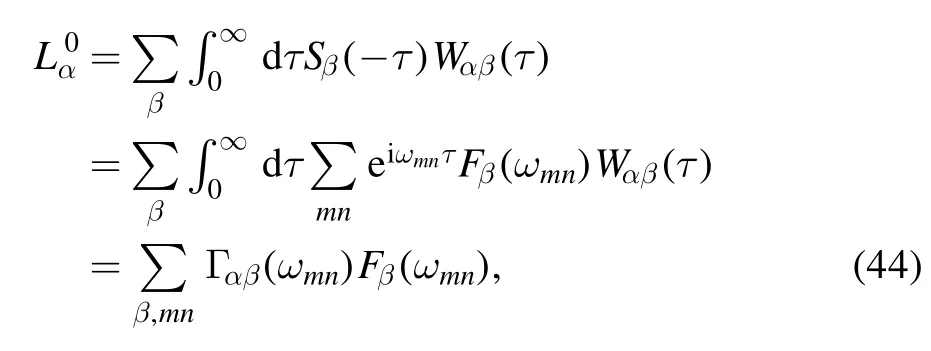
where Γαβ(ωmn) is the Fourier transform of the bath’s correlation function; we call this the spectral correlation tensor of the bath,and it is defined as

Therefore,we have

Inserting equations(42),(44),and(46)into equation(11),we can obtain

and

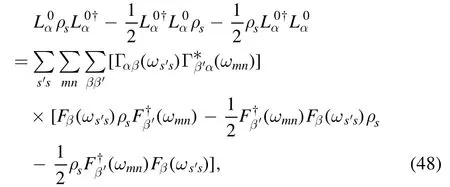
and

Thus,we have

Similarly,we have

In equation (51),the third equality holds,which is based on the fact that when we exchange the indexes α and β,and the variablesωs′sand ωmn,the first term of the right-hand side of the equality does not change.We denote

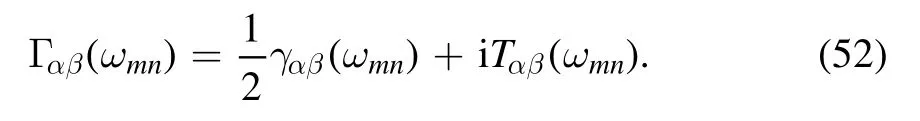
So,we have

and

Thus,we can obtain equations (13) and (14).

Appendix B

The matrix form of equation (19) reads

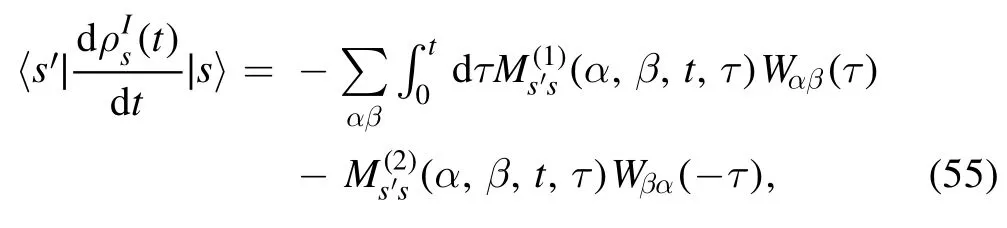
with

and

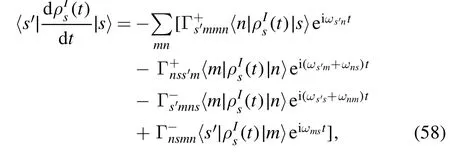
where

Using equation (59),we have

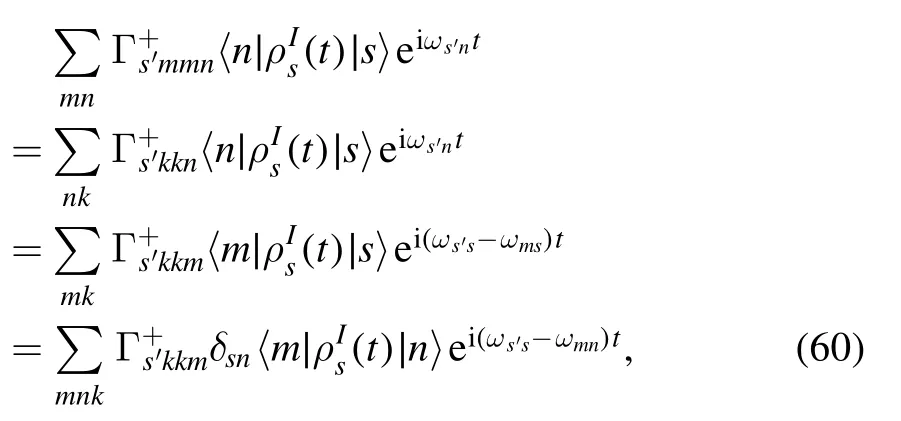
and

Substituting equations (60),and (61) into equation (58),we can finally obtain the Redfield equation in the interaction scenario as equation (22).