一种提高非完整小圆弧曲率半径参数评价精度的方法*
2021-09-27罗智孙吴国新何小妹何学军朱春梅
罗智孙,吴国新*,何小妹,何学军,朱春梅
(1.北京信息科技大学 现代测控技术教育部重点实验室,北京 100192;2.中国航空工业集团 北京长城计量测试技术研究所,北京 100095)
0 引 言
非完整小圆弧指的是圆弧轮廓对应中心角度小于120°的、曲率半径范围为0~25 mm的弧线或弧面[1]。非完整小圆弧轮廓性能特殊,在国防科技工业和精密制造业中得到了广泛应用,例如:航空发动机叶片的前后缘轮廓对发动机的气动性能和叶片的疲劳性能产生直接影响;数控机床刀具的刀尖部分直接决定其加工精度;一些精密零部件的边缘倒角用于去除加工毛刺,改善零部件应力集中的情况。
曲率半径参数作为小圆弧轮廓的核心参数,其精度对工件的生产制造性能极为重要,存在精确测量及评定的迫切需要[2]。然而,其非完整性和圆弧半径范围小的特点导致测量及评价难度大,因此,对曲率半径参数估计的准确性一直存在着争议。
通过已有文献对非完整小圆弧评价方法的研究,基本确定了影响曲率半径评价结果的主要圆弧参数,以及各参数对评价过程影响的大致趋势[3]。影响评价精度的主要圆弧参数有圆弧的理论半径、圆弧轮廓点集所对中心角,以及圆弧轮廓点集的轮廓度误差[4]。在通常情况下,圆弧的理论半径越小,评价的难度及误差就越大;圆弧轮廓所对中心角度越小,曲率半径评价的准确性也越差;轮廓点集的轮廓度误差越大,评价精度也随之下降[5]。
在上述3个影响因素中,圆弧半径是要求取的目标值,无法对其进行调节。因此,学者们普遍从圆弧轮廓点集所对中心角,以及圆弧轮廓点集的轮廓度误差上着手,通过减小轮廓度误差的影响或者增大中心角度的方法,以此来提高其评价的精度。
GUEVARA I等[6]提出了一种基于平均绝对误差来拟合一组点的鲁棒几何方法,该方法通过最小化到数据点的几何距离之和,基于梯度或二阶导数的快速迭代算法,以左、右导数确定迭代新方向,将数据点拟合成圆弧,继而求取半径;该算法在计算效率上可作为常规算法的替代方法,原理上降低了轮廓度误差对评价过程的影响,增强了算法的鲁棒性,使其对异常值和数据噪声不敏感,进而提升了评价精度。FEI Zhi-gen等[7]从非完整小圆弧所对中心角度着手,采用了一种基于径向基函数神经网络(RBFNN)的双向预测方法,将观测数据视为时间序列,并对其进行了双向延伸,再进行了插值,通过增大圆弧长度进而增大圆弧轮廓所对中心角度,经过大量数据的训练学习,最终证实该方法拟合的稳定性和准确性远胜于预测之前。
在一些特定领域及工况条件下,以上方法具有很好的应用效果,但都具有一定的局限性。如基于径向基函数神经网络(RBFNN)的双向预测法,所需圆弧轮廓数据样本量巨大,实际工程中可供用于训练学习的圆弧数据样本数量基本难以达到要求,其应用的普适性不高。不过,此种试图在一定时间跨度内通过预测延长圆弧长度的方法亦是一种可行手段。
基于这种启发,笔者提出一种基于自适应三次指数平滑预测模型的方法,对已有的圆弧轮廓数据点集进行预测延伸,针对传统三次指数平滑预测中平滑系数难以确定的问题,在其基础上添加自适应算法,进行优化。
1 小圆弧轮廓所对中心角对曲率半径参数评价的影响
非完整小圆弧曲率半径参数评价的难点之一在于其非完整性,即轮廓中心角占总圆或球面的比例[8]。圆弧轮廓所对中心角度越小,说明这段圆弧的完整性也越差;完整性差意味着该段圆弧所缺失的信息较多[9],直接导致拟合过程中的不确定因素增多。
因此,在完整性较差的圆弧的拟合过程中,不仅采用不同拟合方法情况下拟合的结果相差很大;采用同种方法对同一圆弧数据拟合,每次的拟合结果也不尽相同。非完整小圆弧曲率半径参数评价的难点主要在于拟合的稳定性及重复性差,直接导致曲率半径估计的准确性也存在争议。
在利用某光学三坐标测量仪测量一件圆心角为10°左右的非完整小圆弧标准件时,经处理后得到轮廓数据点集,再使用测量仪自带软件将其拟合成圆;由于圆弧数据所对中心角过小,缺失信息太多,每次拟合圆的圆心位置与曲率半径参数的结果差异性很大,重复性比较差,难以判定哪次拟合的结果才是准确的。
其拟合效果如图1所示。
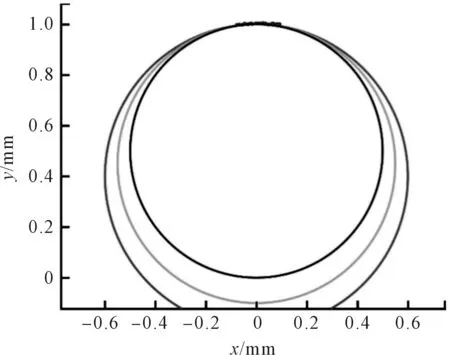
图1 非完整小圆弧曲率半径评价的难点
在非完整圆弧的拟合评价过程中,影响圆弧轮廓数据的曲率半径参数评价精度的因素有:理论半径R、轮廓所对中心角θ和轮廓度误差f等。
为了能对轮廓中心角参数进行更准确地分析,在仿真分析过程中,需控制其他的影响因素不变,即在对一组小圆弧轮廓数据点集进行分析时,应保持半径与轮廓度误差不发生改变,调整中心角度慢慢增大,观察圆弧轮廓数据点集所对应中心角度对曲率半径参数评价结果的影响趋势。
笔者采用3组理论半径分别为0.05 mm,1 mm以及25 mm的圆弧数据点集,轮廓度误差均为理论半径值的14%左右,使用最小二乘法拟合,得出不同半径的小圆弧轮廓数据的评价误差随中心角度增大的变化趋势,如图2所示。
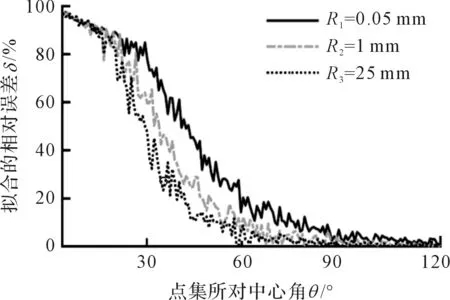
图2 小圆弧中心角度对评价影响的趋势图
由图2可知:在非完整圆弧的评价过程中,不同半径圆弧数据的评价误差变化趋势基本一致,都随着轮廓所对中心角度的增大而减小,评价误差的变化率均呈现出先增大再减小的趋势;
当圆弧中心轮廓角度小于10°或者大于60°时,曲线较平稳,通过增大中心角减小评价误差的方法效果不太明显;反观约15°~60°之间的圆弧,随着中心角度的增大,误差曲线下降的速率快,评价精度提升的效果最为明显。
基于以上仿真分析的结果可知:针对轮廓中心角为60°以下的非完整小圆弧曲率半径参数评价上的难点,可利用一种增大圆弧所对中心角度的方法,来降低曲率半径参数评价过程中的误差。
在所有能增加圆弧长度的方法中,时间序列预测法作为一种常用外延方法而被广泛应用[10]。
2 三次指数平滑法的预测模型
时间序列预测就是通过分析其历史数据的规律性,来研究其未来的变化趋势。一般来说,历史数据对未来值的影响是随时间间隔的增长而递减的,所以,更切合实际的方法是对各期数据进行加权平均求取预测值[11]。
简单加权平均法用的是算术平均数,近期数据的权值比远期数据的权值大,即越近的数据对预测值的影响越大[12]。
指数平滑法是一种特殊的加权平均法,其原理是将权值按照指数递减的规律分配。根据平滑的次数不同,分为一次指数平滑法、二次指数平滑法和三次指数平滑法;每个算法都是在之前的算法基础上再进行一次平滑运算处理得到的。一次指数平滑法适用于无趋势效应、平滑序列的预测;二次指数平滑法适用于线性时间序列数据的预测;三次指数平滑法适用于非线性变化、规律性较差的数据[13]。
在本文的研究中,笔者将圆弧轮廓数据点集根据其空间位置顺序视为时间序列,其大体趋势呈线性变化。但从精密测量的角度分析,由于圆弧表面粗糙度及测量过程中存在误差,实测数据点的规律性并不高,采用三次指数平滑法预测的精度更高。
笔者将实际测量所得的小圆弧轮廓数据点集按照空间坐标位置排序,并将序数视为时间序列的期数,对之进行三次指数平滑。其数学模型如下:
已知圆弧采样点坐标点集X=[x1,x2,x3,…,xn],Y=[y1,y2,y3,…,y…n],三次指数平滑预测模型为:
(1)

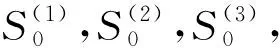
(2)
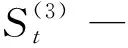
同理,对Y进行三次指数平滑处理。
利用式(2)可求得:
(3)
at2,bt2,ct2的求解同理。
将求出的at1,bt1,ct1和at2,bt2,ct2代入式(1)中,设定好预测的期数m,即可得到后期的预测值。
在三次平滑过程中,为增强预测的准确性,各个参数的选取需要依照一定的要求。接下来对主要参数及其选取标准分别进行分析。
2.1 平滑初值的选取
在平滑过程中,若历史数据样本较小,初始值对预测值影响较大,则取前3或前5组数据的算术平均值为平滑的初值;若样本量大,初始值对预测值影响较小,则取第一组数据作为平滑初值[14]。
2.2 平滑系数的选取
在指数平滑过程中,选择合适的平滑系数α是提高预测精度的关键[15]。α值越大,加权系数序列的衰减速度越快,所以α值实际起着控制参加平均的历史数据对预测值影响的作用,α值愈大意味着历史数据对预测值影响越强。
在平滑系数选取过程中往往遵循以下准则:
(1)若序列的基本趋势较平稳,预测偏差由随机因素造成,则α应取小一些,以减小修正幅度,使预测模型能包含更多历史数据的信息[16];
(2)若预测目标的基本趋势已经发生系统的变化,则α应取大一些,以偏重新数据对原模型进行大幅度修正,使预测模型适应预测新目标的变化[17]。
在实际应用中,α的取值范围一般在0.1~0.3为宜。
2.3 预测步数的选取
在三次指数平滑预测过程中,可采用一步预测或者多步预测,一步预测即是固定式(1)中的m值为1,每次预测只得到一个预测点,预测后将该预测点并入点集重新进行下一期数据的预测;多步预测的m不为1,即可通过一次预测获得多期的预测点。
在两种预测方案的选择上,多步预测虽然能减少迭代计算的次数,提升计算效率,但是由于预测的过程中对于趋势变化的反应速度不如一步预测,导致后期预测数据的准确性不如前期预测数据;随着预测期数增加,误差累加导致后期预测点容易产生偏离,无法进行长期的精确预测[18]。
而用一步预测时,每预测一期数据后便将该数据纳入数据点集,虽然迭代次数增多,计算时间更长,但一定程度上减缓了误差累积的速率,使预测点在多次预测后依然保持较高的准确性,能够将圆弧外延的角度进一步增大,对于曲率半径评价精度提高更有帮助。
因此,在精度要求较高的小圆弧轮廓数据的预测上,一步预测的性能上要优于多步预测。
此处笔者采用三次指数平滑预测模型,对一组轮廓对应中心角为15°左右的圆弧数据点集进行预测,其结果如图3所示。
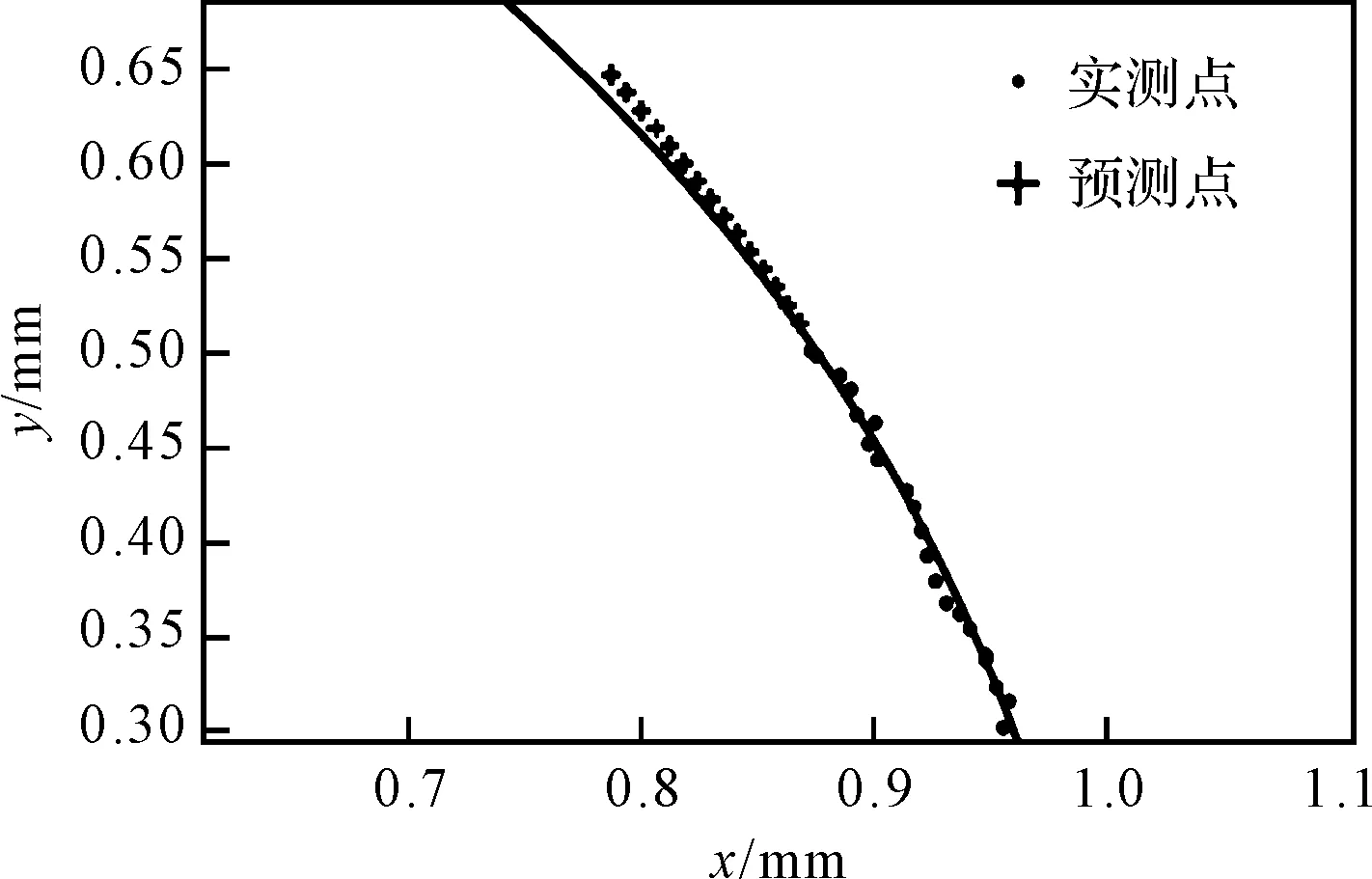
图3 三次指数平滑预测发散图像
由图3可知:对比使用Hough变换法拟合的该组数据的圆弧曲线,可观察到虽然前期的预测点具备一定准确度;但随着预测期数的增加,后期的预测点相对于拟合的标准圆弧发生了较明显的偏移,并且偏移量逐渐增大。
在对图3进行分析时,将预测点出现偏离的原因锁定在平滑系数的确定上,仅凭借实际运用经验确定的平滑系数显然具有一定的局限性;并且,由于每次迭代计算后都会将预测点并入点集,使得预测的样本量逐渐增大,预测趋势发生细微改变,平滑系数却依然是第一次预测前使用的值。
因此,针对如何提高预测结果准确性的问题,最佳平滑系数的确定策略亟待优化。
3 自适应三次指数平滑预测模型
在三次指数平滑的过程中,平滑系数的选取常常带有较强的主观性,由于没有实际值与预测值比较,无法确定其是否为最优系数。
另外,在传统三次指数平滑模型中,平滑系数一旦确定便无法再进行调整,对于样本环境波动的适应能力差,仅适用于一次预测。当一次预测结束后,新产生的预测点再并入数据点集中进行下一轮预测,样本的数量发生改变,再使用该平滑系数进行计算就可能不太适用了。
并且,由于实测数据点集数量过大,预测一个点需要点集所有的点都代入进行迭代计算,增加了许多不必要的繁琐计算;根据时间序列预测的原理,越是靠前的历史数据对预测值的影响越小,远期数据的影响几乎可以忽略不计。
为解决以上两个问题,笔者提出了自适应三次指数平滑预测模型,即在原来传统三次指数模型的基础上添加自适应算法进行优化。
自适应三次指数平滑预测模型并不是像传统的三次指数平滑法一样,将所有点全部代入直接预测,而是根据现有的数据点集,从第一期数据开始,只截取其中部分点进行三次指数平滑;计算出这一期的预测数据后,就往后移动一步计算,每次移动都将最先一期的数据剔除,并加入后一期实测数据。
同时,遍历平滑系数α的取值空间,进行定步距计算,得出一系列预测点,将所有预测点与当期的实测点进行比较,根据误差平方和最小化原则,得出误差最小的预测点,反推出预测该点的平滑系数值,即为实时最佳平滑预测值。
经过前期历史数据的训练,可拟合出平滑系数α的变化趋势曲线。在点集外进行预测时,由于缺少实测值的比较,则需要根据α的拟合曲线方程计算后期平滑系数值,直接利用该平滑系数参与计算预测实测数据点集外的数据点。
自适应三次指数平滑算法流程如下:
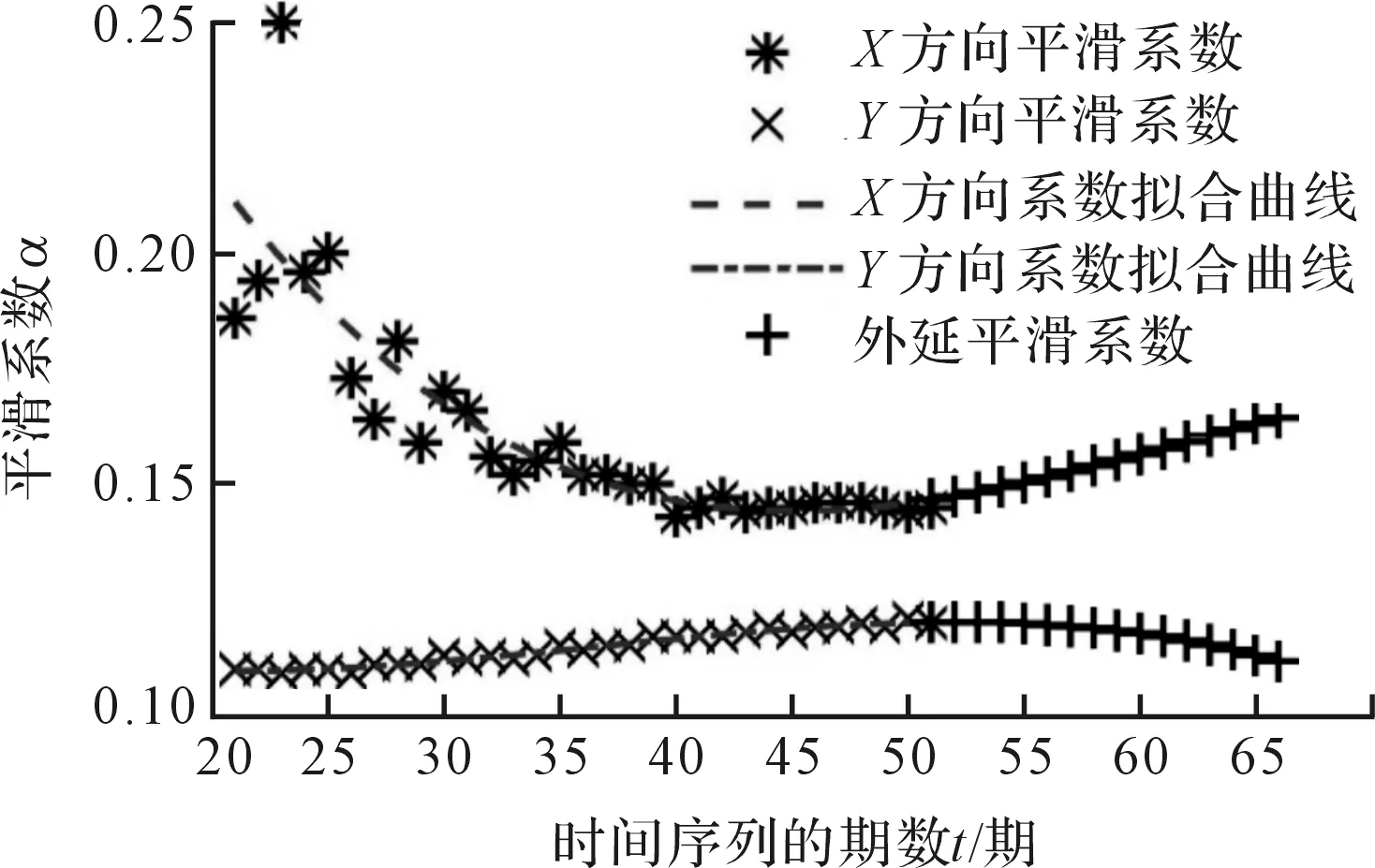
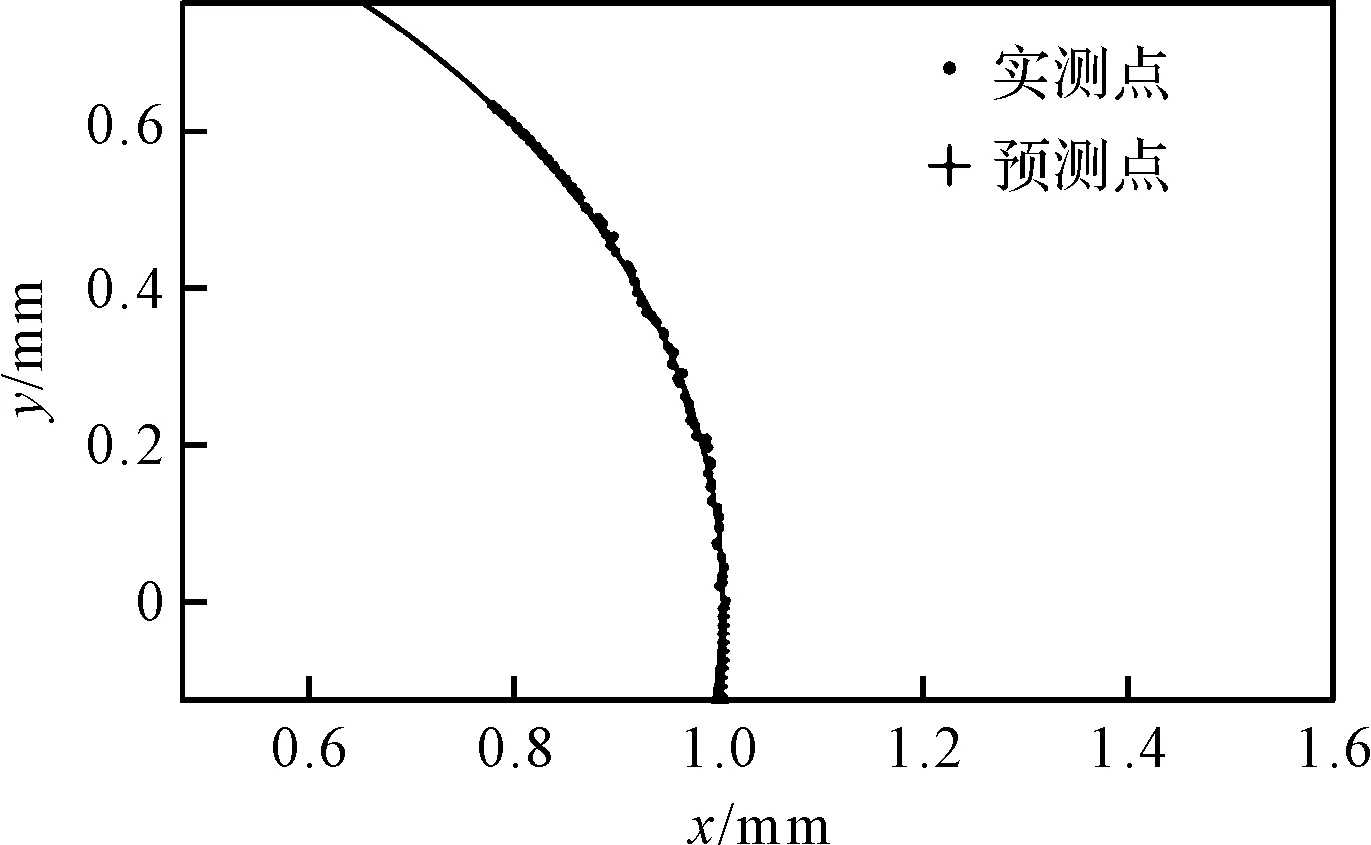
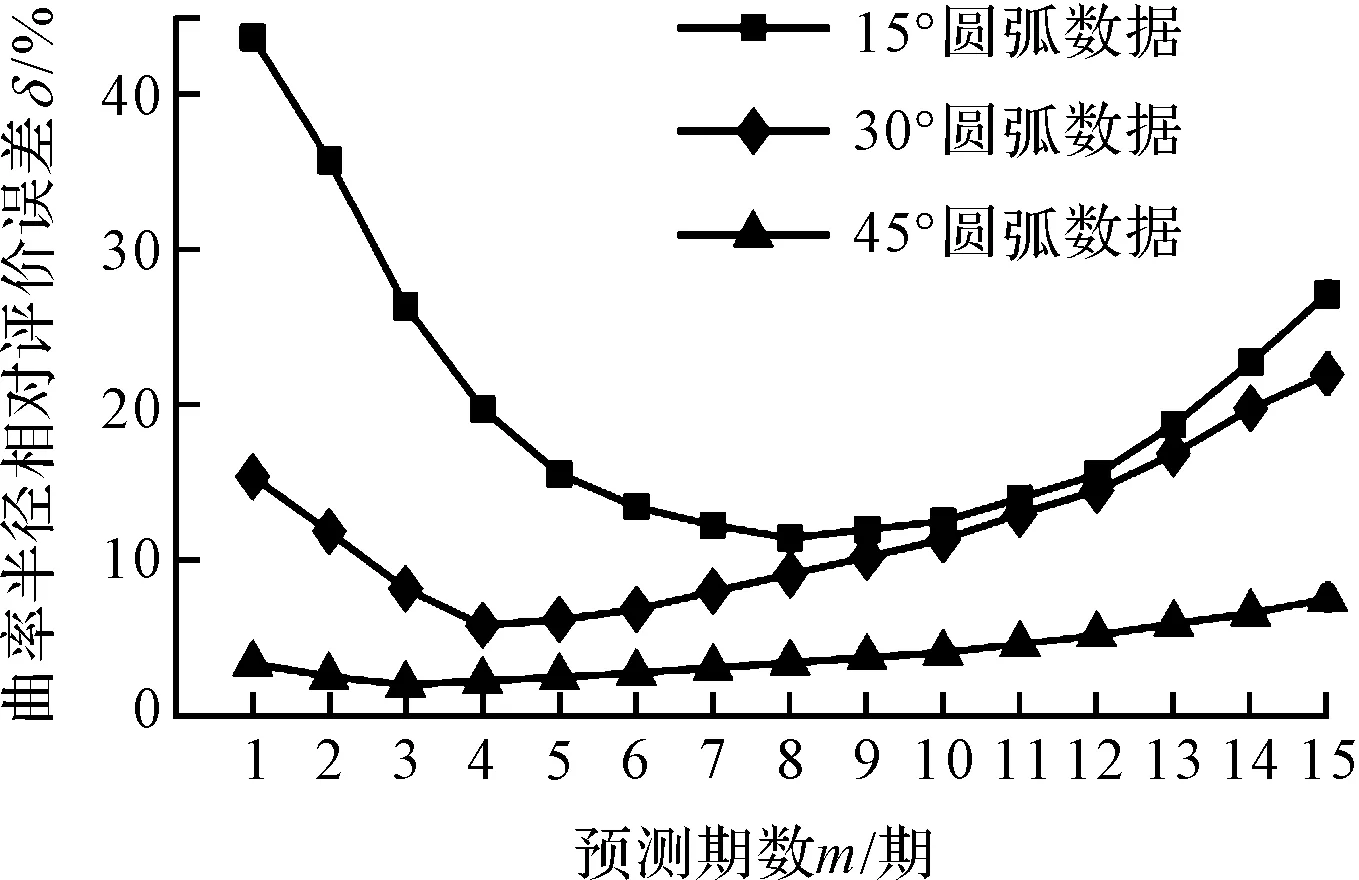
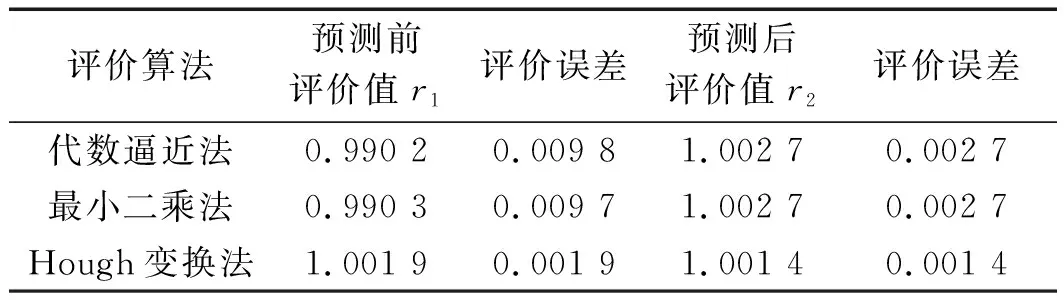
(1)利用现有实测数据横纵坐标点集X和Y,实测样本点个数为n,假定每次预测固定采用k期(k (2)去掉第1期数据,采用第2期至第k+1期实测数据,重复(1)中步骤,得到最佳平滑系数α2,以此类推,总共能得到n-k个α值; (3)使用MATLAB的polyfit函数,将α1到αn-k拟合,得到拟合曲线与拟合公式,计算αn-k+1,αn-k+2,…αn-k+m(其中:m—数据点集外预测的期数); (4)当计算移动至使用第n-k期到第n期数据计算第n+1期预测数据时,将平滑系数αn-k+1代入进行(2)中三次指数平滑预测,每次预测后均将预测点并入点集,并剔除最早一期的数据;以此类推,使用第n+m-k-1期到n+m-1期数据,代入αn-k+m计算第n+m期预测值; (5)将数据点集按逆序排列,即第1期数据变为第n期,第n期变为第1期,重复步骤(1)~(4); (6)将原数据点集与预测数据点集合并形成新数据点集,利用评价方法进行曲率参数评价。 自适应三次指数平滑法固定样本移动计算示意图如图4所示。 图4 自适应三次指数平滑固定样本移动计算示意图 相比于传统三次平滑系数α的确定,自适应三次指数平滑模型的优点在于,能根据时间序列自身的变化来实时监测并调整α的值,每次迭代过程在取值空间内寻找平滑系数最优解;并且在迭代过程中移动计算,固定了时间序列样本的数量,规避了由于预测的样本量改变而产生的影响,更有助于客观观察α的变化趋势,以及用于后期点集外平滑系数的确定。 每次用于计算的样本点数量k的取值同样会影响预测的结果。样本点过多则导致迭代的次数减少,得到平滑系数的个数不够,不利于其拟合以及观测其变化趋势;样本点过少则容易受轮廓点集数据的偶然误差影响,导致平滑系数的波动较大,可能出现偏离较大的点,同样不利于平滑系数α的拟合。 因此,在每次预测样本k值的选取上,一般取总数据点个数的40%~50%左右。至于样本外预测点的个数m的确定,则需要经多次实验,分析不同圆弧数据下预测的最佳期数。 笔者使用9组理论半径分别为0.05 mm、1 mm、25 mm,轮廓对应中心角梯度分别为15°、30°和45°的数据点集,点集的轮廓度误差均在理论半径值的2.6%左右,点集个数均为50个;利用自适应三次指数平滑法进行数据的双向预测,再用最小二乘法评价曲率半径,与直接使用最小二乘法进行比较,分析两种情况下的曲率半径评价精度的变化情况。 此法的原理即是利用前期数据来分析出平滑系数的变化趋势,再通过该趋势调整后期平滑系数,利用得到的平滑系数,进行实测轮廓数据点集外的数据点预测。在前期每一次迭代遍历搜索最佳平滑系数的过程中,将步长设定为0.001,α的取值空间为(0,1)。为提高迭代速度,减少不必要的计算,可根据实际情况缩小α的取值范围;固定每次用于预测的样本点个数k值为20。 因此,在整个移动迭代过程中,由50个实测点集数据可得到30个α值,观察α值的变化趋势,通过对之拟合得到变化曲线及变化公式,利用变化公式,即可求取后期用于点集外数据预测的平滑系数,利用得到的α值,继续进行固定样本数移动计算,就能到准确的轮廓点集外预测点。 平滑系数α的变化趋势及拟合如图5所示。 图5 自适应三次指数平滑系数拟合图及后期推导值 在平滑系数拟合的过程中,笔者使用MATLAB的polyfit函数对其进行拟合,不同拟合次数后期的α变化趋势具有一定差异性。经多组数据综合分析可知,在二次拟合、三次拟合和四次拟合中,选择三次拟合具有更高的拟合优度。 使用与图3中同一组轮廓对应中心角为15°左右的圆弧数据点集,笔者进行自适应三次指数平滑预测。 预测后的拟合结果如图6所示。 图6 自适应三次指数平滑法双向预测拟合效果图 由图6可知:对比图3中单独使用三次指数平滑的预测结果,添加自适应优化后预测的误差明显减小,大大延缓了误差累积的速度,使后期预测点相对于理想圆的偏移量减小了许多;预测的角度增大,使圆弧外延的长度得以增加。 笔者采用不同角度的圆弧数据,进行预测后的误差比较,其结果如图7所示。 图7 不同角度下的预测误差比较 经过以上数据的评价分析结果,验证了自适应三次指数平滑预测方法应用在非完整小圆弧曲率半径参数评价上的可行性。 经初步验证,在使用最小二乘法评价曲率半径参数时,使用自适应三次指数平滑法处理轮廓对应中心角小于60°的圆弧后,具有提高评价精度的作用;并且,随着预测次数的增加,评价误差呈现先减小再增大的趋势,即存在最佳预测期数的问题。 经过对评价误差变化趋势的原因分析可知,短期内预测的数据比较精准,可提高曲率半径参数评价的精度;但随着预测期数的增加,中长期预测数据的误差会慢慢增大。 从上述实验中可观察到:对于15°的小圆弧,双向预测的期数m取8期时最佳,评价的误差最小;对于30°的小圆弧,预测期数m取4期时最佳;对于45°的小圆弧,预测期数m取3期时最佳。用各数据点集相邻两点的夹角乘以对应最佳期数,可求出各组不同角度圆弧数据预测的最佳角度。 经计算可知,各组圆弧数据预测的最佳角度均在5°左右波动,此时,评价误差减至最小,对评价精度的提升效果最佳。 在上文中,为方便计算均使用最小二乘进行曲率半径参数评价,在不同中心角度轮廓数据下,笔者分析了采用该方法对评价的影响。 为验证自适应三次指数平滑法应用的普适性,即在使用其他评价方法时,对非完整小圆弧的评价精度依然具有提高的效果,笔者以一组理论半径为1 mm,圆心角为30°,轮廓度误差为0.026 4的数据点集为例,并根据上节的结果,取预测期数m为4,对其进行自适应三次平滑处理,再分别使用代数逼近法、最小二乘法和Hough变换法,评价曲率半径参数值;并将其与原来未使用自适应三次指数平滑处理前的曲率半径参数评价结果进行比较,预测前后的评价误差分析。 不同评价方法在预测前后评价误差分析如表1所示。 表1 不同评价方法在预测前后评价误差分析(单位:mm) 经过以上不同评价方法下的分析可知,对比使用不同评价方法,自适应三次指数平滑法预测处理均有不同程度的提高;对于最小二乘法及代数逼近法这种代数和最小化原理的参数评价方法,比之Hough变换法这种参数空间内寻优的评价方法,经预测后的精度提升效果更明显。 实验结果表明:相比于未处理直接评价的方法,使用自适应三次指数平滑法对圆弧轮廓数据进行处理后,再利用评价方法进行曲率半径评价的方法,曲率半径的评价精度得到了提升;并且,该方法对于60°以下的非完整小圆弧的评价精度提升效果较为明显;角度越小,评价精度的提升就越大。 在使用该方法时预测圆弧点集数据时,将圆弧对应中心角度增加5°左右最佳,此法对于不同评价方法均能提升评价的精度,具备一定的普适性。 在研究非完整小圆弧曲率半径参数评价方法中,笔者基于仿真分析的方法,计算了一定轮廓度误差下轮廓所对中心角度对评价过程的影响趋势;然后,根据仿真结果分析,针对解决60°以下完整性较差的圆弧在曲率半径参数的评价上存在的难点,提出了一种基于自适应三次指数平滑预测模型的方法,增大了圆弧轮廓中心角度,进而提升了曲率半径参数评价的精度。 笔者通过采用不同圆弧数据进行了多组对照组实验。实验及研究结果表明: (1)使用该方法处理60°以下的非完整小圆弧轮廓数据点集后,再对数据进行评价,评价精度得到了进一步提升。并且,利用此方法将圆弧轮廓增大5°左右,对评价的精度的提升效果最佳; (2)该方法具有一定的普适性,可作为一种前期的数据外延方法,配合各种评价方法对小圆弧曲率半径参数进行精确评价,为提高非完整小圆弧曲率半径参数评价的稳定性与准确性提供了一种有效解决方案。 在下一步的研究工作中,笔者将配合各类不同原理评价方法的使用,进一步研究曲率半径参数评价精度的具体提升效果及其内在联系。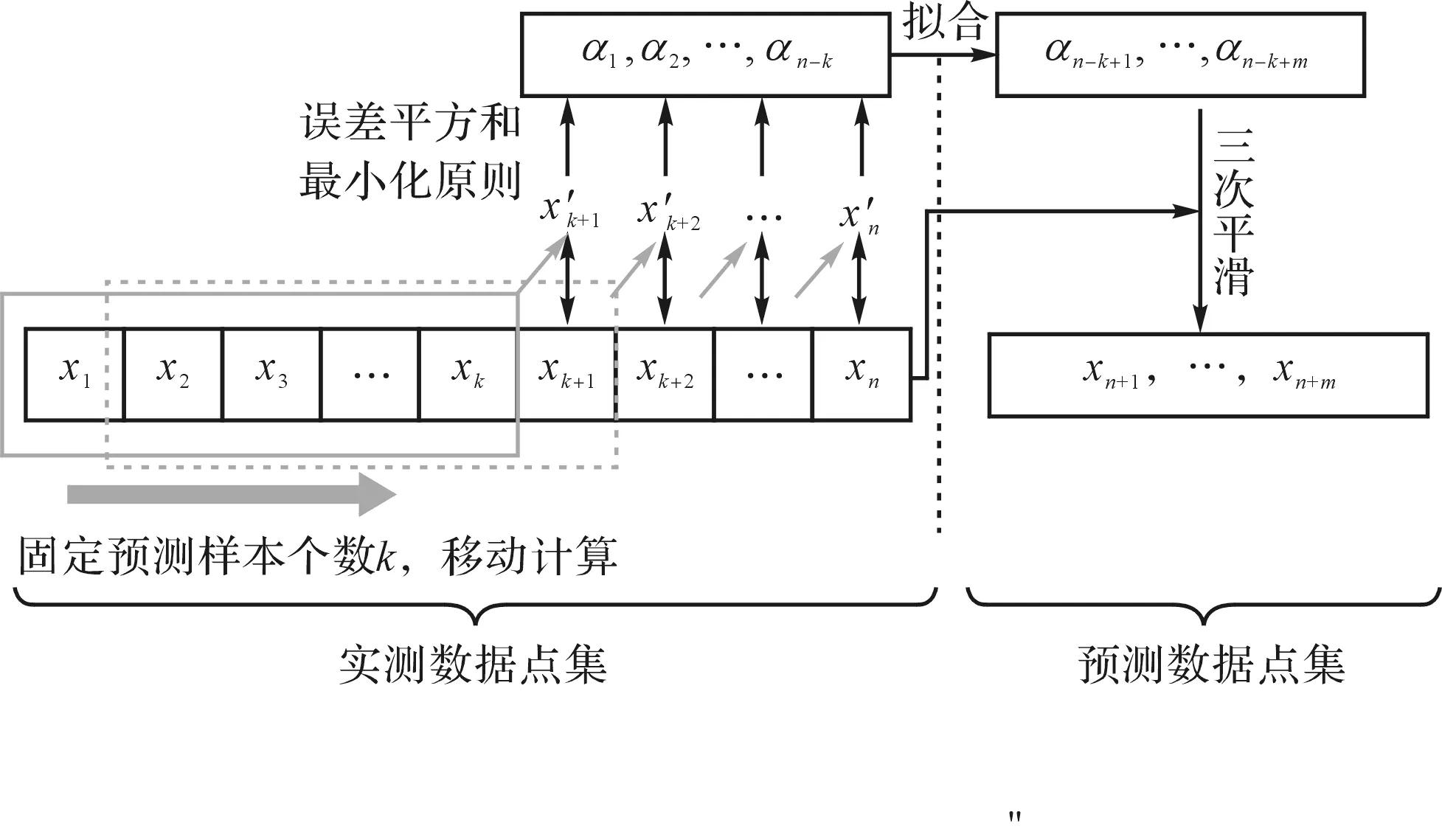
4 实例计算及精度分析
4.1 不同圆弧数据预测前后评价结果比较
4.2 不同评价方法预测前后评价结果比较
5 结束语
