圆柱度最小区域的一般化判别方法*
2021-09-09黄美发唐哲敏刘廷伟
秦 玲 黄美发 唐哲敏 刘廷伟
(①桂林信息科技学院,广西 桂林 541004; ②桂林电子科技大学机电工程学院,广西 桂林 541004)
圆柱度误差是机床轴类零件的一项重要几何误差,它在国标和ISO中的严格评定方法是最小区域法[1-2]。
圆柱度最小区域的几何判别条件比较复杂、条目繁多,标准中列举了7条几何判别条件,并指出还存在其他几何判别条件变式。
为了减少圆柱度等形状误差的判别条件款项,丁喜波等和熊有伦从不同角度提出了基于几何学的统一判别方法[3-5],统一了各类形状误差的判别,但具体操作和计算仍较复杂,因此,目前几何误差的最小区域判别方法大多与具体评定算法相关。凸包法等计算几何方法先归纳所有可能的包容区域,再通过枚举找到其中最小者,即判别方法为数值上的“区域最小”[6-7],这类方法能准确判定最小区域,但不适合测点较多的情况。自适应变动体法、搜索逼近、旋转投影法等基于圆柱或同轴圆柱的几何特性来构造边界圆柱并搜索大小更合适的包容边界,直至满足最小区域的几何判别条件[8-11]。极差法、切比雪夫逼近法及有效集法等从各自优化理论的角度建立形状误差的模型后,分别提出与各自优化理论适应的判别方法[12-14]。牛顿法、二分法等传统优化方法和差分进化算法、混合教与学算法等智能优化算法的判别方法通常为两次迭代间步长或函数值的变化较小[15-18];当出现争议时,这类方法仍需要采用几何判别方法裁定。
综上所述,在经常需要处理大量测点数据的当下,还缺乏一种一般化的、程式化的最小区域判别方法,以便在出现评定争议时裁定算法是否找到了最小区域。因此,本文基于边界点矩阵研究圆柱度的一般化的、程式化的判别方法。分析圆柱测点集与最小区域边界之间的空间关系以及最小区域成立条件的数理逻辑形式,并利用边界点集矩阵的性质提出一种最小区域的一般化判别方法。最后,通过1个评定实例验证了提出的圆柱度一般化判别方法。
1 圆柱度包容区域模型
1.1测点集与包容区域的空间关系
孔轴的圆柱度误差是包容孔轴表面测点集的两个同轴圆柱间“环形柱”区域的大小,其数值与坐标系的选取无关。因此可以将坐标系z轴固定于同轴圆柱的共同轴线上,以便于描述最小区域问题中的基本要素——测点集、边界圆柱,如图1所示。
在建立的坐标系中,测点集可以描述为测点pi的集合{pi|pi= (xi,yi,zi),i= 1, 2, …};测点pi到边界圆柱轴线(z轴)的距离为ri= (xi2+yi2)1/2;外圆柱的半径RU= maxri,内圆柱的半径RV= minri,截面环尺寸L=RU-RV;测点集{pi}自由度方向为沿x、y轴的平动dx、dy和绕x、y轴的转动dα、dβ。

当按自由度方向调整测点集相对于边界圆柱的方位时,边界测点pi的方位变化趋势dpi如公式和图1所示。
(1)
式中:Rdα、Rdβ分别为测点绕x轴、y轴运动的坐标变换矩阵,E3×3为单位矩阵;自由度趋近于0,因此sin dα趋近于dα,sin dβ趋近于dβ,自由度的余弦值趋近于1,自由度的积趋近于0。
1.2 包容区域的大小及其变化趋势
边界圆柱和测点集有相对方位变化趋势时,边界圆柱的大小变化趋势仅取决于边界测点pi。边界测点pi到z轴距离的变化趋势dri,即dpi在径向上的投影,如图2所示。将pi处指向z轴的径向单位向量Ni= (-xi/ri, -yi/ri, -zi/ri)T代入公式,可以得到dri的代数表达式,如式(2)所示:

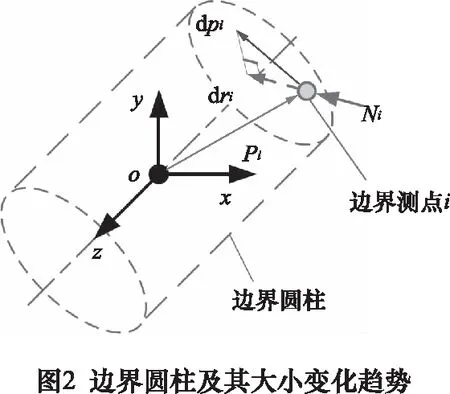
为便于分析,可以将式(2)中pi自由度运动趋势合记为运动趋势向量Ψ= [dx, dy, dα, dβ]T,Ψ的系数合记为运动系数向量Ai,如式(3)所示。
Ai= [xi/ri,yi/ri, -ziyi/ri,zixi/ri]
(3)
将Ai、Ψ代入式(3),可以得到dri的线性向量表达式,如式(4)所示。
AiΨ=dri
(4)
记v∈V、u∈U分别为与内、外圆柱接触的测点序号集,则内圆柱变化趋势dRV= min drv,外圆柱变化趋势dRU= min dru,两个同轴圆柱间的“环形柱”大小变化趋势dR= dRU- dRV。代入式(4),可以得到dR的向量表达式,如式(5)所示。
dR= max dru- min drv=max(Au-Av)Ψ
(5)
2 圆柱度最小区域的一般化表达
2.1 圆柱度最小区域逻辑的基本形式及变形
测点集圆柱度的最小区域可以一般性地描述为:测点集与“环形柱”间的相对方位已调整至最佳,相对方位发生任意改变时,在内外圆柱上各至少存在1个边界测点使“环形柱”不会更小。据此可以建立最小区域逻辑的基本形式,如公式所示,其中dru,v为上边界点pu和下边界点pv到z轴距离的变化趋势之差。
(∀Ψ)(∃(u,v))((Au-Av)Ψ=dru,v≥0)
(6)
式(6)并不便于分析,因此转而分析其互斥的否命题形式,如式(7)所示。
(∃Ψ)(∀(u,v))(Au,vΨ (7) 其中,记b<0,Au,v=Au-Av为pu与pv的运动系数差向量。如果公式不成立,则“环形柱”为测点集的最小区域。否则,“环形柱”不是最小区域。记A= […,Au,v, …]T为边界点集的运动系数差矩阵,b= […, dru,v, …]T,则公式(6)等价于公式(7)。 (∃Ψ)(∀(u,v))((AΨ=b)∧(dru,v 设外圆柱测点数目为m1,内圆柱测点数目为m2,rank(A) =r,则Au,v共有m=m1m2个,A共有m行。当rank([A,b]) =rank(A) =r时,AΨ=b总是有解,公式总是成立,“环形柱”不是最小区域。下面讨论rank([A,b]) >r时公式的成立条件。 定义1:在AΨ=B中任选r个线性无关的运动系数差向量Au,v、对应的dru,v及常数项b,分别集合成矩阵Ar、常数项br及常数项Br;线性方程组ArΨ=Br的解集Fj= {Ψ}j就是不等式组{Au,vΨ 通过定义1,可以将式(8)中AΨ=b的行重新排列,如式(9)所示。 (9) 因为rank(A) =r,所以可以得到关于Au,vΨ界限的性质,如公式所示。 (∀Ψ)(∀(u,v)∈s)(Au,vΨ≠b) (10) 记 则由式(10)可以得到关于Au,vΨ大小的性质: (11) 由式(11)可知,可以先求解方程ArΨ=Br的1个解Ψ*,然后考察Ψ*是否满足P2(Ψ*),即可判断相应的基本解集Fj= {Ψ*}是否为有效基本解集。 总结本节内容,可以得到空间直线度最小区域统一判别方法的基本流程,如图3所示。 本节以实际轴的同一组测点数据为对象,分别用自适应变动体法[8]和优化法[15]评定实际轴的圆柱度。 针对2种方法的评定结果的争议,用本文提出的方法辨别哪种方法准确构建了圆柱度的最小区域,以验证提出的判定方法。 本例用三坐标测量机(Hexagon Metrology, Qing Dao, GLOBAL CLASSIC SR 07. 10. 07)对轴表面进行光学扫描,测点如图4所示。 在MATLAB R2014a中,自编程序实现文献[8]中的自适应变动体法,得到被测轴的圆柱度为0.156 mm,构成最小区域的边界测点的序号为1 560、95、67、90、1 527、48,如表1所示。自适应变动体法基于圆柱的几何特性来构造边界圆柱并逐步搜索更小的包容边界,直至满足最小区域的几何判别条件,流程较为复杂,限于篇幅,请感兴趣的读者自行查阅文献[8]。 表1 评定结果 mm 在MATLAB R2014a中,根据文献[15]建立圆柱度最小区域优化函数,如式(12)所示,其中:Vx、Vy、Vα和Vβ是自由变量,Vx、Vy分别为“环状柱”相对于原始坐标系x轴、y轴的微小平移量,Vα、Vβ分别为“环状柱”相对于原始坐标系x轴、y轴的微小旋转量,Xi、Yi分别为测点pi相对于“环状柱”轴线的坐标。 (12) 用线性高斯牛顿法(MATLAB R2014a中内置的fminun函数)求解相同的轴的圆柱度(测点数据相同),得到被测轴的圆柱度为0.176 mm,构成最小区域的边界测点的序号为11 936、1 595、1 560,如表1所示。高斯牛顿法主要根据目标函数的偏导数来构造迭代公式,以逐步找到目标函数的最优解、最优值,是传统的优化方法,在MATLAB R2014a中有集成的函数。因此,文中仅列出圆柱度最小区域优化函数,恕不详述高斯牛顿法求解过程。 从表1中可以看到,自适应变动体法和线性高斯牛顿法找到的边界点集不同,即两种方法的解不同。同时,从表1中还可以看到,两种方法求得的结果(圆柱度)也不相同。两种方法的评定对象相同,而解和结果不同,出现了争议。为了裁定2个评定结果间的争议,基于提出的判别方法,用自编程序分别判别两种方法是否构造了最小区域。 (1)用提出的方法考察自适应变动体法 将自适应变动体法求得的边界测点代入公式,可以求出运动系数向量Ai及运动系数差向量Au,v,如:A1 560,90的计算如公式所示。 A1 560,90=[A1 560-A90] =[1.103 1 3.815 4 -22.860 2 12.678 9] (13) (2)用提出的方法考察线性高斯牛顿法 出于一般性考虑,表1中线性高斯牛顿法的结果是在初始解为零向量的条件下计算得到的。同时,为了减少计算误差和截断误差对判别结果的影响,距离内外边界圆柱小于0.001 mm的点都考虑为边界点。将线性高斯牛顿法求得的边界测点代入公式可以求出运动系数向量Ai及运动系数差向量Au,v,如A1 936,48为: A1 936,48=[A1 936-A48] =[1.103 1 3.815 4 -22.860 2 12.678 9] (15) 将m=m1m2= 3×2 = 6个Au,v集合为A,如式(16)所示。 指定(m= 6)个(b=-1)并将其集合为b,可以求出rank([A,b]) =rank(A) = 4;因此,公式总是成立,“环形柱”不是最小区域。 (3)用基于梯度的方法考察线性高斯牛顿法 内置函数输出标识符显示线性高斯牛顿法迭代精度达到10-6mm后终止迭代。结合判别结果可知,初步估计线性高斯牛顿法陷于局部最优解。 为验证线性高斯牛顿法是否确实陷入局部最优解,将自适应变动体法求得的“环状柱”相对于原始坐标系的平移、旋转量作为线性高斯牛顿法的初始解。此时,线性高斯牛顿法的最优解与自适应变动体法一致,为0.156 mm,如表2所示。求得的边界点也与自适应变动体法一致。这证实了高斯牛顿法所求得解是局部最优解。 如表2所示,当线性高斯牛顿法的迭代解处函数梯度较小时,基于梯度的判别方法会认定算法找到了最小区域,以保证算法效率。然而,这种方法有可能会被局部最优解或局部低梯度区域所误导,不适合作为出现评定争议时的裁定方法。 从表2中还可以看出,提出的判别方法能判定自适应变动体法求得的“环状柱”为最小区域;能判定以零向量为初解的线性高斯牛顿法陷入了局部最优解,未找到最小区域;还能判定以自适应变动体法的解为初解的线性高斯牛顿法求得的“环状柱”为最小区域。因此,提出的判别方法行之有效,适合作为裁定评定争议的方法。 表2 判别方法及评定方法比较 分析了孔轴外表面测点集与最小区域边界之间的相对空间关系,利用数理逻辑形式、线性方程组和不等式组的性质,以线性矩阵及流程图的形式,提出了孔轴圆柱度最小区域的统一判别方法。提出的判别方法是一种程式化的、一般化的代数判别方法,由简单的重复运算、条件选择构成,可以在出现评定争议时裁定算法是否找到了最小区域。 分别用线性高斯牛顿法和自适应变动体法评定了1个实际轴的圆柱度,用提出的方法分别检验了两种方法的评定结果。提出的判别方法识别了自适应变动体法和线性高斯牛顿法求得的最小区域,也识别了线性高斯牛顿法求出的局部最优解,具备裁定评定争议的能力。 本文推导了圆柱度最小区域的一般化判别方法,其中运用的自由度、法向量、数理逻辑、线性理论等也适合其它形状的最小区域评定。未来可以参考本文方法继续研究直线度、轮廓度等形状误差的最小区域判定。2.2 基于逻辑表达式的一般化判别方法
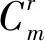
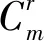

3 实例验证
3.1实际轴的圆柱度评定



3.2 评定结果的争议和判别
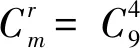
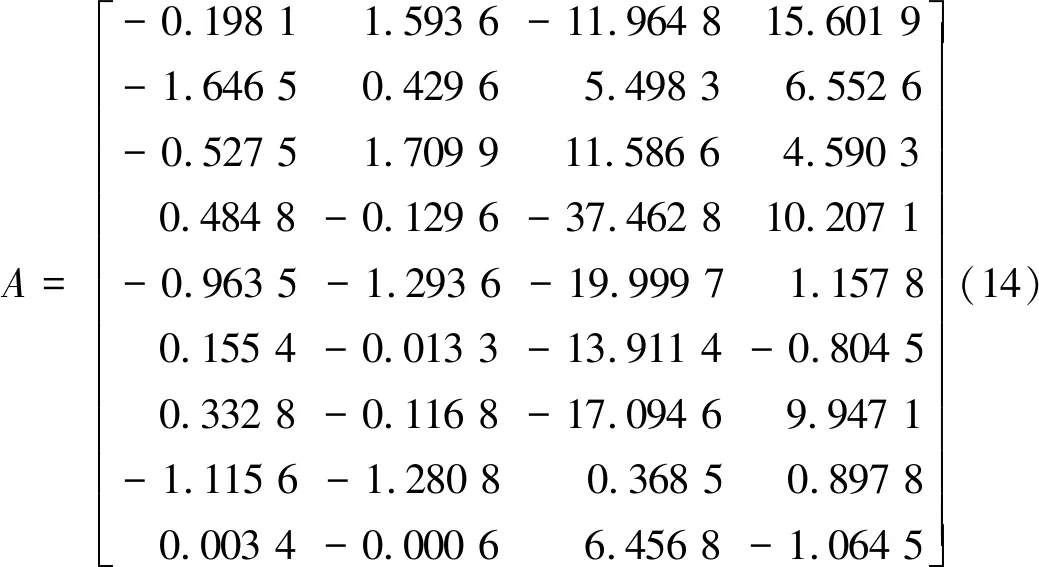

3.3 判别结果及结论
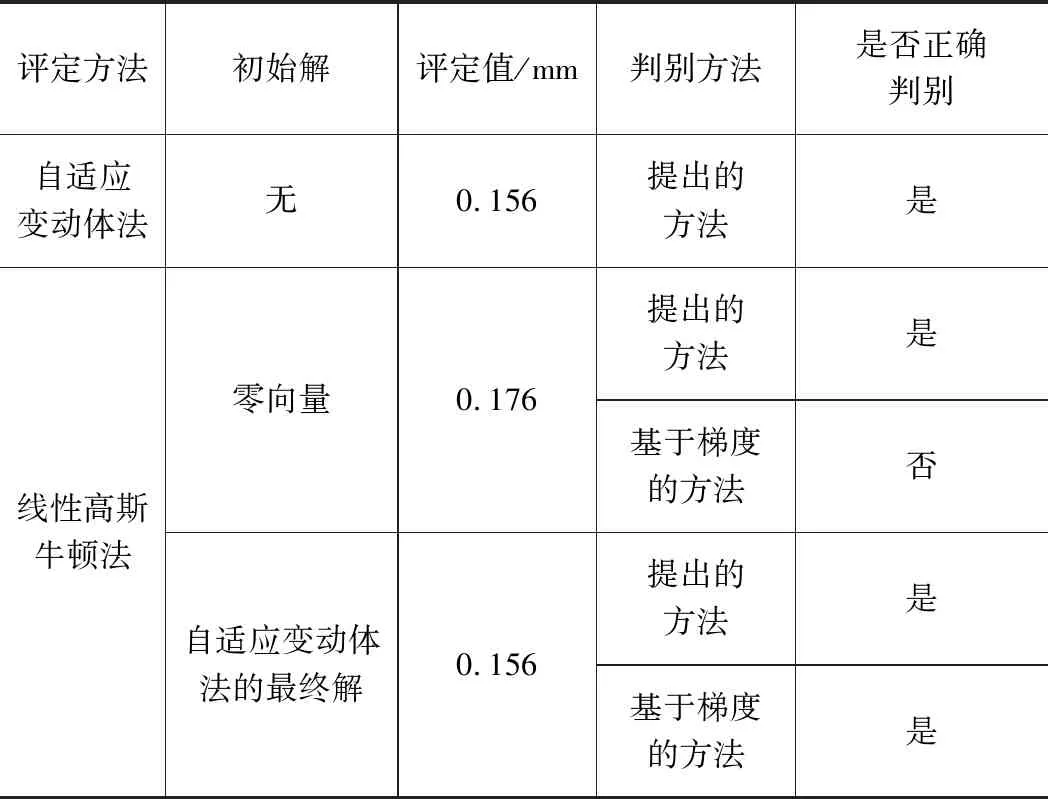
4 结语
