刘全慧

(湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙 410082)

几何是人类直觉的基本来源，抽象的理论问题常常借助几何图像而变得浅易．古希腊甚至有几何神圣(Sacred Geometry)的信仰，柏拉图就认为上苍以几何创世 (God geometrizes continually)，影响深远．现代物理建立在黎曼几何、闵可夫斯基几何等几何基础之上，规范场理论为自然界的基本相互作用的提供了统一的数学基础，而规范场理论是一种几何理论，即所谓的纤维从理论．可以说，几何是物理学的基础．

物理学图像，常常是指几何图像．进入大学后，几何必须借助于微积分才能获得深入的理解．因此，大学中的物理图像就应该是微分几何图像．请回忆Fermi对Dyson关于物理计算的教诲,首先是物理图像(physical picture)[1]．原话是：“One way, and this is the way I prefer, is to have a clear physical picture of the process that you are calculating．The other way is to have a precise and self-consistent mathematical formalism．”[1]既然物理学中的几何无处不在，热力学也不能例外．从教学的角度，如果从几何的角度审视热力学中的一些难题，会发现一些困难问题变得浅易．必须指出，物理课程中微分几何的应用不足，是一个普遍存在而又可以轻易解决却几乎普遍忽视的问题．参见笔者近作[2]．这个问题，国外教学实践时间最长，做得较为成熟的是诺贝尔物理学奖获得者Thorne小组．经过在加州理工和斯坦福大学37年的教学实践之后，他们于2017年出版了一本的全新的大学物理教材《现代经典物理》(全名是Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics)．特点就是用几何重塑了经典物理学．前言中特别声明了如下特点：“几何学是本书中的深入主线，和非常重要的经纬．我们将看到如何通过洗练的几何思考就可决定或强烈限制了经典物理学的基本原理．几何学不仅能凸显经典原理的特征，还有助于将它们与相应的量子原理关联起来．进一步，几何方法可以避免冗长的分析计算．尽管相关的冗长、常规的计算，有时难以避免， 在这种情况下，我们有时会求助于现代符号运算软件Maple，Mathematica和Matlab如来节省空间．”[3]. 换句话说，吹掉物理学上计算难度上的灰尘，发现物理学中到处都是几何．

在热力学建立的过程中，曾受到了几何的影响，吉布斯热力学图像法(Gibbs’ Thermodynamic Graphical Method)[4]是吉布斯文集卷I第一、二篇论文的题目．麦克斯韦利用这一图像法，制作了三维的热力学曲面[5,6]．但是，这一传统没有很好地传承下来．现在的热力学的教科书中，较少能看到几何的作用，这可能是热力学显得抽象难以理解的一个重要原因．

Thorne小组的实践说明，可以尝试从几何角度审视全部的热力学，但是他们的教材并没有涉及热力学，而我们也不可能靠一篇短文做到这一点．本文将在几何框架下具体分析了如下3个问题．第1个问题是，从切触的角度，分析汤姆孙-贝特洛原理．而汤姆孙-贝特洛原理是热力学第三定律的实验基础．第2个问题是，从二维曲面高斯和平均曲率的角度，分析van der Waals方程中a,b系数是否和温度有关的问题．第3个问题是，从黎曼几何分析涨落的(准)热力学理论．最后一节是讨论和结论．

如果没有特殊说明，本文所用的符号取其通常教材中的熟悉的含义．

1 汤姆孙-贝特洛原理与热力学第三定律

1.1 数学准备：两个函数的切触及其切触的阶

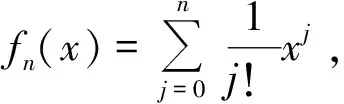
两个函数的切触即二维空间中两根曲线的接触的定量描述，在三维空间中两个曲面之间也有类似的接触．

1.2 两个函数的切触与汤姆孙-贝特洛原理

考察热力学中一幅熟悉的图1，即汤姆孙-贝特洛原理的图示．从这幅图可以立即看出两根曲线ΔG和ΔH在T=0处具有一阶切触．

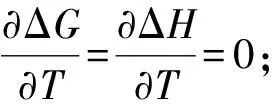
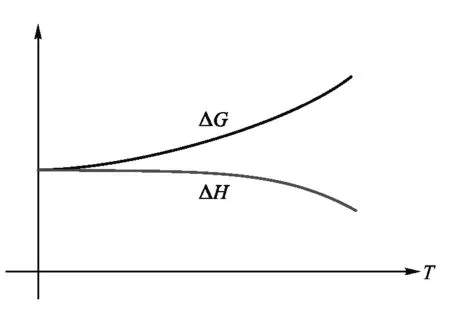
图1 汤姆孙-贝特洛原理的图示

图1中的两根曲线开口方向值得注意．根据等温过程的如下关系ΔG-ΔH=-TΔS，实验上只告诉反应是放热的，即ΔS0,换言之，有ΔG>ΔH．从这一点出发，判别不了曲线ΔG和ΔH随温度变化的开口方向相反．两条曲线同时上凸、下凹，或者二者开口方向相反，都有可能．为什么仅仅考虑二者开口方向相反呢？从几何的角度，两条曲线同时上凸或者下凹，这些是二阶切触．可惜的是，这不是最普遍的情况．所有的情况，都包含在一阶切触中．即一阶切触是最普遍的情况．因此，图1中曲线的开口方向不是最普遍的情况，但是一阶切触包含在所有实验中．

2 van der Waals方程中a、b系数是否和温度有关？

2.1 数学准备：二维曲面上的高斯和平均曲率

考虑一个一般性的二维曲面方程p=p(T,V) ，注意，不要把这个方程误解为普通的物态方程，除非p、T、V都已经无量纲化．平均曲率H和高斯曲率K包含了所有一阶和二阶导数，但是表达式比较复杂，不给出具体形式．一般而言，高斯曲率为正的点，曲面局部形状类似于球面或者椭球面；高斯曲率为负的点，曲面局部形状类似于马鞍面；高斯曲率为零的点，曲面局部形状类似于猴鞍面或者平点．

由于我们感兴趣的主要部分是临界点的形状，因此，我们给出临界点上平均曲率H和高斯曲率K的结果如下

(1)

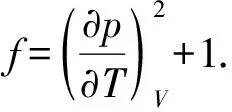
2.2 van der Waals方程的普适性

不失一般性，假设van der Waals方程中的a、b系数依赖于温度

(2)

(3)

临界温度和临界体积、临界压强和临界温度之间的关系如下

(4)

对van der Waals方程进行无量纲化处理，即p以pC为单位，V以VC为单位，T以TC为单位，分别记为p*、V*、T*，同时，a(T)、b(T)分别以a(TC)、b(TC)为单位，记为α(T*)、β(T*)，则van der Waals方程的形式是

(5)

当a,b系数为常数的时候，即

α(T*)=β(T*)=1

(6)

可利用从微分几何的算出临界点的平均曲率H和高斯曲率K(计算直截了当，但过程稍长，从略)：

(7)

第一个结果表明临界点是一个极小曲面，第二个结果即高斯曲率为负数．从几何的角度，表明临界点是一个马鞍点．

结果(7)中的a、b系数不依赖于温度．如果a、b系数依赖于温度，立即发现平均曲率和高斯曲率分别为(计算过程从略)：

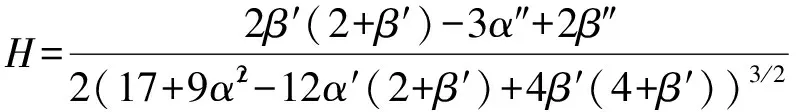
(8)

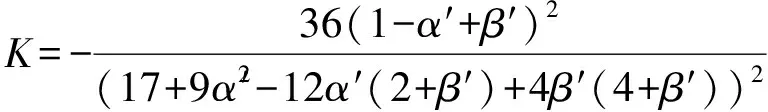
(9)

其中，f′(x)=df/dx，等等．很明显，只要如下条件不满足

α′=1+β′

(10)

则高斯曲率在全部区域内为负数，处处都是马鞍点，这和实际物态定性不符, 参考图2, 清楚显示出临界点不是马鞍点．不过，我们仅仅关心临界点附近点物态方程的行为．于是van der Waals方程中的a、b系数至少一个依赖于温度．如何选择a、b系数，需要和具体物质的实验曲线进行比较[8]．

需要指出的是，van der Waals方程中的a、b系数是否依赖于温度，是一个教学和科研中的难点[8]．

图2 气液相变临界点实验结果图(图取自网站[9]授权使用)

3 涨落的度规描述与标量曲率

考虑一个孤立系统S(0)中的一个小部分，把这一小部分当成我们研究的热力学系统．这部分(系统)的和其它的部分(库)可以有能量、体积和粒子数的交换．用较长或者粗粒化的时间尺度下，系统和库处于平衡状态；而在较短的时间尺度(例如两个分子间平均碰撞时间尺度)下，系统处于不停的涨落中，这个自发涨落也可以较大或者产生宏观可观测的后果．当然，也可以用外加干扰的方式强迫系统偏离平衡态，然后考察系统回复到平衡态过程．

根据涨落的(准)热力学理论，当系统偏离平衡态的概率是[10,11]

W∝exp(ΔS(0)/k)=

exp(-(ΔE-TΔS+pΔV)/kT)=

exp(-(ΔSΔT-ΔpΔV)/kT)

(11)

这是求系统涨落的一般性理论．在这个理论中，没有高级项，不能适用于临界点．或者说我们还没有一个可以包含高级项贡献的自洽的涨落的(准)热力学理论．注意到指数上的量是广延量，只需要考虑到单位体积内的结果．这个结果具有两个性质：第一，是一个物理的不变量：

(12)

第二，不同的热力学坐标下，有不同的形式：

(13)

和

(14)

等等，其中v为单位体积，cV、cp分别为单位体积中的定容和定压热容量．这些表达式可以获得不同热力学量的涨落的表达式．但是，这些不同的表达式都没有彻底表达出它们蕴含的几何含义：这些表达式都是同一个热力学系统或者黎曼流形上的线元长度的平方，即式(13)和(14)中出现了两个不同的坐标选择，而一定有些物理量，例如热力学的标量曲率，和坐标的选择没有关系．

注意到式(13)和(14)给出了两个不同的度规：

(15)

和

(16)

既然有了度规，就可以求标量曲率R：

(17)

其中，g=|gμν|是度规矩阵的行列式．热力学标量曲率，是热力学几何中的一个核心物理量[12]．这是一个热力学量，但是携带了相互作用的信息[12]．

下面研究两个度规矩阵(15)和(16)之间的关系．由于

(18)

即

(19)

由此可以进一步证明这两个度规给出相同的标量曲率．

为了显示出热力学曲率的确是分子之间相互作用的一个刻画，利用常数a、b参量的van der Waals方程，并假定热容量为常数，立即得

(20)

其中n为单位体积中的粒子数．注意van der Waals方程适用于流体体积较大的时候．这个时候，关注式(20)中的领头项，立即发现热力学曲率和正比于分子之间的吸引力参数a，领头项前面的负号，表明分子之间的相互作用为吸引力．

有人可能认为引入热力学标量曲率是锦上添花．事实远非如此．黑洞热力学是理论物理的一个研究热点，是一个确立的学科．但是，解析黑洞的微观结构是一个非常困难的问题[13]，通过分析热力学的标量曲率，可以为理解黑洞的微观结构提供重要的启示[13]．

4 讨论和结论

热力学中，尽管勒让德变换的几何解释为大家所熟知，但是几何的使用还远远不够．本文从书本中的三个熟悉的知识点进行了微分几何分析，发现了热力学和几何的深刻联系，希望能滋养我们的教学甚至研究并产生出新的结果．

本文的目的有两个．第一，在一些常见的热力学问题中，通过挖掘几何内涵可以达到曲径通天的效果，解决热力学疑难问题．第二，无论教学还是科研，积极思考甚至“胡思乱想”是非常必要的．这些思考中包含的启发性非常可贵，因为这里有创造的萌芽．