张建侠，宋明顺，方兴华，邓钰佳

(中国计量大学 经济与管理学院，浙江 杭州 310018)

0 引言

实践中的优化设计问题通常是多目标优化问题(Multiobjective Optimization Problem, MOP)。由于优化目标之间的冲突性，MOP一般不存在单个绝对的最优解，其目标是寻求一组Pareto最优意义下的折衷解[1](Pareto Set, PS)。智能优化算法(如多目标进化算法)是求解MOP的有效方法，但由于在优化进程中需要大量调用函数，不能满足昂贵仿真情形下的优化设计需求[2]。为提高复杂系统的优化设计效率，基于近似模型的代理优化方法应运而生[3-4]。

Kriging模型可以同时提供任意试验点上的预测值及预测误差，易于构造引导优化过程快速收敛的自适应优化策略[5]。以有效全局优化(Efficient Global Optimization, EGO)算法[6]为代表的自适应代理优化算法，合理利用设计的加点准则序贯选取能收敛到全局最优解的新试验点，优化效率比传统进化类方法高出1～2个数量级[7]。近年来，自适应优化思想逐渐推广至MOP。由于容易理解和执行，学者们常采用直接优化Pareto解集质量指标(performance indicator)的方式优化原MOP[8]。

文献[9]基于超体积(HyperVolume, HV)质量指标，提出了期望超体积改进(Expected Hypervolume Improvement, EHVI)准则及其精确计算方法，并证明了EHVI准则的单调性质;文献[10]对ParEGO等4种多目标代理优化算法进行了比较，指出基于EHVI准则的代理优化算法是唯一一种在求解人工构造问题和实际工程问题时，都表现优异的算法。可行性概率(Probability of Feasibility, PoF)准则能估计试验点落入可行域的概率，在代理优化研究中常被用于设计黑箱约束的应对策略[11]。文献[12]进一步指出，基于PoF准则的约束应对策略不需要拟合拉格朗日乘子函数和选择罚因子，与基于增广拉格朗日乘子法的约束优化策略[13]相比，更易于执行且优化效果好;文献[14]将PoF准则分别与Kriging模型预测标准差和EHVI准则结合，提出了探索MOP可行域和改进PS质量的加点策略。当优化问题包含多个非连通可行子区域时，其可行域探索准则不能确保找出所有子区域，且近似PS改进准则逼近可行域边界上最优解的效率不高[15]。

评估算法的收敛性是代理优化研究的另一课题。文献[16]归类分析了多目标进化算法研究中的收敛准则，并强调了综合应用多个评估指标(如Epsilon、R2等)的重要性。对多目标代理优化算法，代理模型的近似误差将会影响求得的近似PS，因此PS的不确定性反映了算法的收敛性。条件模拟(conditional simulation)与Kriging模型有相同理论基础，但更侧重于对区域变量空间分布的随机模拟，被广泛应用于地质、土壤、水文、生态等领域的不确定性评价[17]。针对固定翼飞机采集地面火灾数据存在采样不足的问题，文献[18]提出了利用Kriging模型和条件模拟拟合火辐射能量密度的方法;文献[19]针对不考虑约束影响的优化问题，分析了条件模拟方法评估算法收敛性的可能性。

为提高黑箱系统多目标优化设计的效率，综合考虑Kriging模型的预测不确定性、试验点的PoF和EHVI、试验点之间的距离，并利用随机集理论，提出一种改进的多目标代理优化算法及收敛性分析方法。该算法对可行域非连通的问题也有效；近似PS改进准则兼具刻画可行域边界的能力；收敛性评估从分析近似PS不确定性的角度评估算法的收敛性。通过两个算例与已有算法作比较，计算结果验证了所提算法的高效性。

1 多目标优化和Kriging模型

1.1 问题描述

一个典型的包含m个目标函数和r个约束条件的MOP可以表示为

s.t.

gi(x)≤0,i=1,…,r;

x∈X⊂d。

(1)

其中：m>1;x为d维设计变量;y(x)为目标函数向量;gi(x)为第i个约束条件。由于优化目标之间的冲突性，MOP通常不存在绝对的最优解，而是寻求一组Pareto意义下的折衷解[1]。设G为问题(1)的可行域，x,x′∈G是两个可行解，称x支配x′(记作xx′)当且仅当：∀i∈{1,…,m},yi(x)≤yi(x′)∧y(x)≠y(x′)。Pareto最优解集(PS)是所有Pareto最优解构成的集合：PS={x∈G|x*∈G:x*x}。PS在目标空间上的投影称为Pareto最优前沿(Pareto Front, PF)：PF={y(x)|x∈PS}。

1.2 Kriging模型

Kriging模型将仿真模型的响应y(x)看作是随机过程的实现，即

(2)

(3)

1.3 其他相关概念

辨识优化问题可行域、改进PS质量是多目标代理优化算法的基本功能。为此，首先介绍以下概念。

(1)期望超体积改进[9]

超体积指的是被PF支配的空间的体积，其取值越大越好。超体积改进(HV Improvement，HVI)则被用来度量新试验数据(x,y(x))带来的超体积的增量。

HVI(x)=HVI(y(x),PF,r)=

(4)

(5)

(2)可行性概率[11]

考虑约束条件的影响，令G={x∈X|g(x)≤0}表示可行域，则新试验点x带来的可行超体积改进为

I(x)=I(y(x),PF,r)=1g(x)≤0·

HVI(y(x),PF,r)

(6)

其中1g(x)≤0为示性函数。若目标函数y独立于约束条件g，则新试验点x带来的期望的可行超体积改进可表示为

HVI(y(x),PF,r))

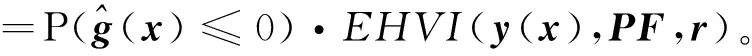
(7)

(3)条件模拟

(8)

2 基于Kriging模型的多目标代理优化算法

本文提出的多目标代理优化算法(Surrogate-based Multiobjective Optimization Algorithm, SMOA)的基本流程如图1所示,包括辨识可行域、改进解集质量及评估解集不确定性3个主要部分。

2.1 辨识可行域和改进近似PF

(1)辨识可行域

若MOP的约束条件较难满足(如可行域较小)，初始样本点集不含可行试验点，则先用以下加点准则选取一个可行试验点：

(9)

(10)

(2)改进近似PF

约束优化问题的最优解通常位于可行域边界上。为此，提出如下兼顾目标改进和可行域边界刻画的近似PF改进准则：

Cpf(x)=maxx∈Ppf(EHVI(x)·PoF(x))。

(11)

式中Ppf表示备选样本集(同时优化EHVI和PoF时求得的Pareto集),

Ppf=maxx∈X(EHVI(x),PoF(x))。

(12)

式中EHVI(x)=EHVI(x,PF,r)表示试验点x的期望超体积改进。从具有Pareto最优性的备选样本集中选取新试验点，不仅缩小了新试验点选择范围、避免在无效区域选取新试验点，还使新试验点兼具了刻画可行域边界的能力，进而提高Cpf(x)准则选取新试验点和改进近似PF的针对性，提高优化效率和稳健性。

2.2 度量近似PF的不确定性

工程实践中MOP的真实PF是未知的，使优化算法的收敛性评估遇到困难(Epsilon、世代距离等解集质量指标需要用到真实PF)。为此，提出一种利用条件模拟度量近似PF不确定性，并将其作为算法收敛性评价依据的间接方法。

(1)条件Pareto前沿(Conditional Pareto Fronts，CPFs)

条件模拟方法生成N个CPFs的步骤见算法1，这些CPFs反映了近似PF的不确定。

算法1生成N个CPFs。

步骤1选取模拟点。

(1)随机生成n个模拟点{e1,…,en}⊂X⊂d。

(2)利用约束条件的Kriging模型，选出“可行”的模拟点{e1′,…,en′}。

步骤2利用条件模拟方法预测目标函数响应值：

步骤3利用“可行”的模拟点及响应数据，生成一个条件PF及条件PS。

步骤4重复以上步骤N次，得到N个CPFs。

文献[22]证明了CPFs在分布上与被其支配的随机集等价。因此，CPFs的不确定性又可借助Vorob’ev期望和方差的概念加以描述[23]。

(2)Vorob’ev期望和方差

定义1收敛函数和上水平集[22-23]。设Y是拓扑空间B⊂m中的随机闭集，定义Y的收敛函数(coverage function)为pY:y∈BP(y∈Y)。利用收敛函数，定义Y的上水平集(upper level set)为Qβ={z∈B,pY(z)≥β}，并称β为分位数。

定义2Vorob’ev期望和方差[22-23]。令m表示m上的勒贝格测度且E(m(Y))≤+∞，若存在β*满足E(m(Y))=m(Qβ*),则定义Y的Vorob’ev期望为其上水平集Qβ*;否则，先用式子{m(Qβ)≤E(m(Y))≤m(Qβ*),∀β>β*}求分位数β*,再令对应的水平集Qβ*为Y的Vorob’ev期望。定义Y与其Vorob’ev期望Qβ*的对称差的期望E(μ(Qβ*ΔY))为Y的Vorob’ev方差。

(3)近似PF的不确定性

算法2评估近似PF的不确定性(求Vorob’ev期望和方差)。

步骤1利用算法1生成近似PF的CPFs。

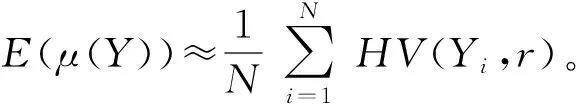
步骤4二分法求Vorob’ev期望的β*分位数

(1)取a=0,b=1。

步骤5利用收敛函数和β*，确定Y的Vorob’ev期望Qβ*(上水平集)。

3 算例与结果分析

本章通过两个典型算例，将提出的SMOA算法与文献[14]的KEMOCO代理优化算法及U-NSGA-Ⅲ[24]进化算法作比较，以验证SMOA算法的有效性、高效性及条件模拟方法评估算法收敛性的可行性。

3.1 数值算例

算例1

f1(x)=(x1-10)2+(x2-15)2+10,

(13)

其中x=(x1,x2)∈[-5,10]×[0,15]。算例1为自构造函数。

算例2[25]

f1(x)=-(25(x1-2)2+(x2-2)2+

(x3-1)2+(x4-4)2+(x5-1)2),

g1=2-x1-x2≤0,

g2=x1+x2-6≤0,

g3=x2-x1-2≤0,

g4=x1-3x2-2≤0

g5=(x3-3)2+x4-4≤0,

g6=4-(x5-3)2-x6≤0。

(14)

其中：x1,x2,x6∈[0,10],x3,x5∈[1,5],x4∈[0,6]。

算例1的可行域由3个非连通子区域组成且可行域占设计变量空间的比例小，可用于验证SMOA算法可行域探索准则的有效性。算例2包含6个变量和6个约束条件，可用于验证SMOA算法在求解较复杂MOP时的高效性和通用性。

3.2 试验设定

为方便分析，首先对算例的变量作归一化处理，使x∈[0,1]d。其次，假定算例的目标和约束条件相互独立，并分别构建他们的Kriging模型(取初始设计的样本容量为k=5×d，其中d为设计变量的维数)。这是由于：优化问题函数之间的相关性信息通常是未知的，且构建多函数联合Kriging模型的过程复杂、易出现数值不稳定，在实践中并未表现出更好的预测精度[26]。

SMOA算法包含两个需要预先设定的参数q和tfea。其中，距离项(D(x))q中的参数q对可行域探索准则Cfea(x)的探索能力有很大影响，经过反复测试，建议对有多个非连通可行子区域的优化问题(如算例1)取q=2，对可行域单连通的优化问题(如算例2)取q=1。鉴于Cfea(x)准则中的距离项能迫使新试验点彼此远离，进而在可行域中分布均匀，此处将用于辨识可行域的可行试验点的数量设定为tfea=10(足以刻画出可行域的轮廓)。此外，本文选取有20个随机初始点的拟牛顿法BFGS算法优化Cfea(x)准则，以保证新试验点选取的准确性；在改进近似PF时，选取种群大小为100、进化代数为200的U-NSGA-Ⅲ算法生成Cpf(x)准则的备选试验点集。

在比较SMOA、KEMOCO以及U-NSGA-Ⅲ算法的优化性能时，本文以试验的总次数T作为SMOA和KEMOCO算法的终止条件，取U-NSGA-Ⅲ算法的种群大小为100、进化代数为200，并选取相对超体积(Relative HV，RHV)、Epsilon和R2指标评估算法的优化性能，用这些指标分别描述近似PF与真实PF之间的相对误差、最大最小距离和平均距离[27]。

3.3 优化结果分析

KEMOCO算法直接以EHVI与PoF的乘积作为近似PF的改进准则。本文SMOA算法首先以同时最大化EHVI和PoF为目标生成具有Pareto最优性的备选点集Ppf，再从中选取新试验点，不仅提高了新试验点选取的目的性，还使其兼具了改进最优解和刻画可行域边界的能力，保证了算法的优化效率和精度。通过两个数值算例，在45组随机初始试验设计下，用SMOA和KEMOCO算法的PF改进准则改进可行域探索阶段得到的近似PF，并与U-NSGA-Ⅲ算法的优化结果作比较，得到的解集质量指标数据如表1所示。表中，算例1的真实PF是通过比较细密网格点上目标和约束函数的取值得到的；算例2的自变量维度高，难以用网格点法确定其真实PF，为此将由U-NSGA-Ⅲ算法(种群大小取200，进化代数取500)求得的“高精度”PF当作真实的PF。

表1 不同优化算法求得的近似PF的质量指标数据(45组)

由表1的指标数据可以看出：用SMOA算法求解算例1和算例2，得到的解集质量指标数据明显优于KEMOCO算法的相应数据(差异性检验结果如表2)，且SMOA算法优化结果的标准差更小。说明本文所提近似PF改进准则(式(11))，兼具了改进目标函数和刻画可行域边界的功能，具有更高的优化精确和稳定性。算例1的优化结果数据还显示SMOA算法和U-NSGA-Ⅲ算法的优化精度在同一数量级，证明SMOA算法具有类似于多目标进化算法的优化能力但优化效率更高(SMOA算法的试验次数是T=80，远小于U-NSGA-Ⅲ算法的试验次数T=20 000)。

表2 SMOA算法与KEMOCO算法优化效果差异性检验(配对t检验，差异性水平0.05)

3.4 算法收敛性评估

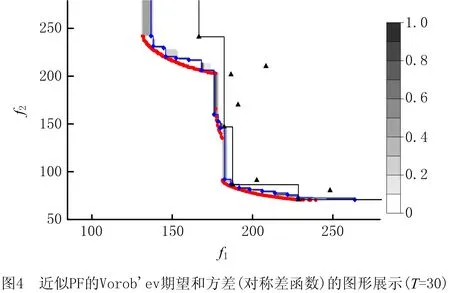
当真实PF未知时，解集质量指标难以评价代理优化算法的收敛性。本文用条件模拟方法分析近似PF的不确定性，并将此不确定性作为算法收敛性的评价依据。用SMOA算法求解算例1，并用条件模拟方法度量近似PF的不确定性，结果如图3～图5所示。图5中圆点对应真实的PF，菱形表示随机集Vorob’ev期望的PF，上三角形表示SMOA算法在优化过程中添加的可行试验数据(它们的连线对应于求得的近似PF)；阴影区域则反映了CPFs的不确定性(y属于对称差Qβ*ΔY的概率)。

由图3可知：在可行域探索阶段选取的前10个试验点中，有4个是可行的且它们成功地找到了算例1的全部3个可行子区域；但此时CPFs的不确定程度高(图中阴影区域大)、SMOA算法求得的近似PF与随机集Vorob’ev期望的PF相差大，算法未收敛。用加点准则Cfea(x)继续选取10个新试验点(如图4)，此时CPFs的不确定性已较小(图中阴影区域较小)，Vorob’ev期望的PF接近于真实的PF，说明当前试验数据包含了PF的较多信息；但SMOA算法求得的近似PF与Vorob’ev期望的PF差异仍然较大，算法尚未收敛。用SMOA算法继续添加新试验点直到总试验次数T=80(如图5)，这时图中的阴影区域已经非常小，且真实的PF、Vorob’ev期望的PF、近似PF三者几乎重合，SMOA算法收敛。

表征近似PF不确定性的Vorob’ev期望和方差的超体积(分别记为VE和VD)，也可由条件模拟方法(算法2)得到。受变异系数概念的启发，在此用VD/VE作为定量分析近似PF不确定性的指标，并与RHV、Epsilon、R2等作比较，结果如图6所示。可知：①VD/VE与RHV、Epsilon、R2等解集质量指标的总体变化趋势一致，表明近似PF的不确定性确实反映了代理优化算法的收敛性；②VD/VE指标的灵敏度略有不足：VE和VD数据的获取涉及随机抽样(用以生成CPFs)，由此产生的随机误差导致VD/VE指标在优化进程的后期不能迅速趋于零；③用条件模拟方法间接分析代理优化算法的收敛性，即便真实PF未知，也能从定性、定量两方面评估优化进程，是一种新颖、可行的算法收敛性评估方法。

4 结束语

针对包含黑箱约束的多目标优化设计问题，本文提出一种有效辨识可行域和提高优化效率的SMOA算法。该算法的可行域探索准则包含了考虑试验点之间距离的项，辨识可行域的能力强；近似PF改进准则从具有Pareto最优性的点集中选取新试验点，选点目的性强且兼具刻画可行域边界，保证了算法的优化效率和精度；此外，用随机模拟方法间接评估算法的收敛性，避免了真实PF未知情况下解集质量指标难以评估算法收敛性的问题。最后，通过与KEMOCO及U-NSGA-Ⅲ算法作比较，验证了SMOA算法的有效性和高效性。由于条件模拟涉及大量模拟点的选取与比较，其计算量较大。如何进一步提高算法收敛性评估中条件模拟的效率以使其适用于高维问题，以及如何在算法的优化迭代中同时选取多个新试验点以充分利用仿真模型的并行计算能力，是需要进一步研究的问题。