赵跃新, 齐望东, 刘 鹏, 袁 恩, 徐 兵

(1.陆军工程大学指挥控制工程学院, 江苏 南京 210007; 2.东南大学信息科学与工程学院,江苏 南京 210096; 3.网络通信与安全紫金山实验室, 江苏 南京 211111)

0 引 言

目标跟踪在无线通信、物联网、雷达声呐等领域得到了广泛的研究与应用,主要包括导航定位[1-2]、侦察监控[3-4]、精确制导[5-6]等方面,旨在利用观测站采集的到达角(angle of arrival, AoA)、传播时间、到达时间差等测量值来估计运动目标的位置和速度。随着阵列天线及其信号处理的技术发展与大量应用,比如5G的大规模天线阵列和波束成形,AoA测量已经在许多低成本硬件平台上得以实现[7-9],使得基于AoA的目标跟踪具有更广的适用范围。

AoA观测方程和目标状态存在非线性关系,使得AoA目标跟踪具有很大的挑战性。由于经典卡尔曼滤波无法适用于非线性状态空间模型,所以需要采用非线性滤波算法处理AoA观测方程。扩展卡尔曼滤波(extended Kalman filter, EKF)通过一阶泰勒级数近似得到线性化的观测方程,但是截断误差使得EKF在初始状态误差和观测噪声较大时容易发散[10]。容积卡尔曼滤波(cubature Kalman filter, CKF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)等Sigma点卡尔曼滤波算法[11-12]并没有近似非线性函数,而是通过选择一组Sigma点近似目标状态的高斯分布统计量,可获得二阶泰勒近似精度,其稳定性更好,但是计算开销大。粒子滤波[13]从后验概率中抽取随机状态粒子并以此表达其分布,可处理非线性模型和非高斯噪声分布,然而计算复杂度很高,难以适用于实时目标跟踪。

与上述非线性滤波算法不同,伪线性卡尔曼滤波[14-15](pseudo linear Kalman filter, PLKF)利用等价运算将AoA观测方程转换为伪线性形式,不需要近似处理非线性函数,可以直接应用线性卡尔曼滤波到伪线性观测方程。PLKF不仅结构简单、计算高效,可满足实时跟踪目标的要求,而且对初始误差十分鲁棒,不容易受到初始状态的影响[16]。然而,伪线性化会使得PLKF产生估计偏差,该偏差不能通过提高观测总数来降低,在观测噪声严重的情况下更为明显,导致跟踪性能急剧退化[17]。

围绕PLKF的偏差问题,改进算法主要分为两类:一类是偏差补偿PLKF[18-19](bias-compensated PLKF, BC-PLKF),另一类是基于工具变量的卡尔曼滤波[17,20](instrumental variable Kalman filter, IVKF)。其中,BC-PLKF通过计算PLKF的估计偏差并进行补偿,以提高跟踪精度;IVKF利用工具变量矩阵减小伪线性噪声和观测系数矩阵的相关性,可以有效降低偏差。随着观测噪声增加,偏差补偿的准确性降低,而工具变量矩阵和观测系数矩阵的相关性减弱,这两类方法都使性能显著降低。对此,采用选择性角度测量IVKF(selective-angle-measurement IVKF，SAM-IVKF)策略[21],当符合SAM条件时使用BC-PLKF的状态估计值构造工具变量矩阵再执行IVKF,否则只需运行BC-PLKF。但是SAM-IVKF本质上还是基于偏差补偿和工具变量思想,并且SAM阈值并不是自适应确定,所以在噪声严重时跟踪性能仍然会出现明显的下降。

针对上述问题,本文将扩展观测矩阵思想[22-23]融入卡尔曼滤波框架,提出了用于三维AoA目标跟踪的二次约束卡尔曼滤波(quadratic constraint Kalman filter, QCKF)算法。该算法通过构造目标函数并附加二次约束以实现状态更新,再利用矩阵扰动方法完成协方差矩阵更新。QCKF的核心思想是引入涉及所有观测噪声项的增广矩阵,接着对等价于线性卡尔曼滤波的目标函数添加二次约束,使其在待估计状态为真实值时达到最小值,以此降低由伪线性噪声和观测系数矩阵之间相关性所引起的估计偏差。仿真分析对比了PLKF、EKF、BC-PLKF、SAM-IVKF、UKF以及QCKF的跟踪性能,充分表明了本文算法的优越性,其均方根误差(root mean squared error, RMSE)在低噪声情况下可达到后验克拉美罗下界(Cramer-Rao lower bound, CRLB),当噪声严重时具有更高的跟踪精度,并且计算复杂度不高。

1 三维AoA目标跟踪

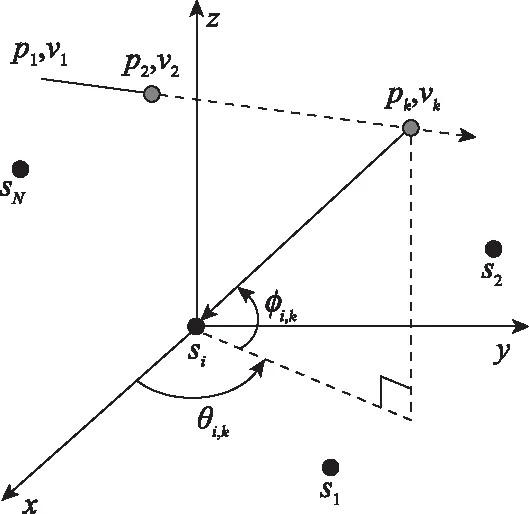
图1 三维AoA目标跟踪示意图

xk=Fk-1xk-1+wk-1

(1)

假设目标进行匀速运动,则Fk和Qk的表达式如下:

(2)

式中:Ts为相邻时刻的采样间隔;Qρ=diag(ρx,ρy,ρz),ρx、ρy和ρz分别为过程噪声在x、y和z坐标轴上的功率谱密度。目标可以通过调整Fk将匀速运动模型替换为匀加速运动、匀速率转弯运动等其他动态模型,同时Qk随之进行相应变化。

在k时刻,目标相对于第i个观测站的AoA包括方位角θi,k和俯仰角φi,k,并且θi,k∈(-π,π)以及φi,k∈(-π/2,π/2),其观测方程为

(3)

(4a)

(4b)

(5)

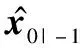
2 PLKF分析

针对AoA目标跟踪的非线性状态估计问题,PLKF是一种简单有效的非线性滤波算法,利用等价运算将非线性观测方程转换为伪线性形式,不采取近似的线性化处理。然而,伪线性化会导致PLKF出现有偏估计,特别是在噪声严重时性能快速下降。因此,本节在推导三维PLKF的基础上,分析其偏差构成及影响,给出引起估计偏差的主要原因。

2.1 PLKF

方位角θi,k的观测方程(4a)通过等价代数运算可转换为

(6)

式中:uθ i,k=[sinθi,k,-cosθi,k,0]T;L=[I3×3,03×3]。在实际情况下,受观测噪声影响的式(6)变为

(7)

同理,俯仰角φi,k的观测方程(4b)等价为

(8)

(9)

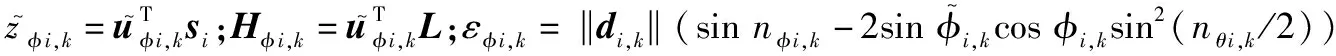
通过组合每个观测站的式(7)和式(9),从而得到伪线性形式的观测方程为

(10)

伪线性方程式(10)与非线性观测方程式(5)相比已转换为线性形式,然后将线性卡尔曼滤波应用于式(1)和式(10)可得PLKF,具体步骤如下。

步骤 1时间更新:

(11a)

(11b)

步骤 2测量更新:

(11c)

(11d)

Pk|k=(I-KkHk)Pk|k-1

(11e)

2.2 偏差分析

(12)

式(12)减去真实状态xk可得到瞬时估计偏差为

(13)

γk=E{σk}=E{σk1}+E{σk2}+E{σk3}

(14)

式中：

估计偏差γk由包括3部分:① 前一个时刻预测值所引入的偏差E{σk1};②Pk|k和wk-1相关性造成的偏差E{σk2};③ 观测系数矩阵Hk和伪线性噪声向量εk相关性引起的偏差E{σk3}。其中,E{σk1}在其余两项偏差等于0时可忽略;Pk|k和系统状态有关,所以与wk-1相关,但对于速度接近恒定的目标,过程噪声较小,使得Pk|k和wk-1相关性很弱,可得E{σk2}≈0。然而,Hk和εk均受到观测噪声影响,其相关性不可忽略,从而E{σk3}≠0。因此,观测系数矩阵和伪线性噪声向量的相关性是PLKF失去无偏性的主要原因,其偏差不会随着观测总数的增加而降低,并且在观测噪声严重时更显著,造成估计性能明显退化。

3 QCKF

为减小PLKF的状态估计偏差,需要降低观测噪声相关性的影响。本文提出的QCKF算法仍使用与观测噪声无关的状态预测方程(11a)及其协方差矩阵方程(11b),然后附加二次约束实现状态更新,再利用矩阵扰动方法完成协方差矩阵更新。

3.1 状态更新

结合线性卡尔曼滤波的状态估计协方差最小准则,可构造等价的目标函数

(15)

(16)

(17)

(18)

(19)

其中，

ηi,k=[0,nθ i,k]T

Λ1,k和Λ2,k的第2i-1行和第2i行(i=1,2,…,N)分别为

Λ2,k(2i-1,:)=0T

其中，

将式(17)和式(18)代入式(16)可得

(20)

为分析噪声扰动矩阵ΔAk和ΔBk对状态估计偏差的影响,对式(20)取期望可得

(21)

由于ΔAk和ΔBk的均值为零矩阵,所以式(20)的右侧第3项在式(21)中也等于0。根据式(17)中ΔAk定义,可得

(22)

(23)

(24)

式中的约束值μk可取任意正数,约束矩阵Ωk的表达式为

(25)

式中：

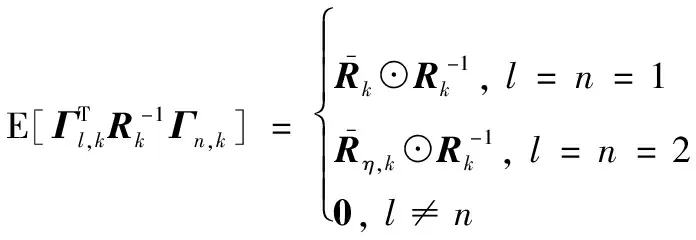
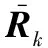
由于具有等式的二次约束优化问题式(24)可通过拉格朗日乘子法进行求解,所以需要最小化的辅助目标函数为

(26)

式中：λ为拉格朗日乘子。通过式(26)对mk求偏导,并令其等于0,可得

(27)

(28)

(29)

3.2 协方差矩阵更新

由于状态更新采用广义特征值分解进行优化问题的求解,所以无法直接利用解析表达式推导协方差矩阵。对此,本节结合约束条件,利用矩阵扰动方法完成协方差矩阵更新。

(30)

(31)

式中：Φ1,k和Φ2,k的第2i-1行和第2i行(i=1,2,…,N)分别为

Φ2,k(2i-1,:)=0T

(32)

将式(32)代入式(24),然后约束优化问题等价于

(33)

(34)

(35)

(36)

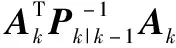
(37)

(38)

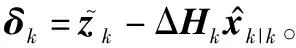
(39)

(40)

(41)

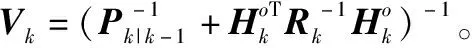
(42)

结合式(41)和式(42),可得

(43)

Tk((Φ2,kTkDk)⊙Θk)12N

(44)

式中：

Θk=blkdiag{Θ1,k,Θ2,k,…,ΘN,k}

(45)

(46)

结合观测方程伪线性化、二次约束状态更新及其协方差矩阵更新,QCKF算法的流程总结如下。

算法1 QCKF输入: x^k-1|k-1,Pk-1|k-1,Fk-1,Qk-1,R-k,y^k,S=[s1,s2,…,sN]时间更新: x^k|k-1=Fk-1x^k-1|k-1 Pk|k-1=Fk-1Pk-1|k-1FTk-1+Qk-1观测方程伪线性化: [z^k,Hk]=pesudo-linear(y^k,S) ∥式(7)和式(9)Dk=f(x^k|k-1,S) ∥Dk定义于式(10)之下Rk=DkR-kDTk测量更新: 构造增广矩阵:Ak=[-I,x^k|k-1],Bk=[-Hk,z^k] 计算约束矩阵:Ωk ∥式(25) ^mk=min{eig(ATkP-1k|k-1Ak+BTkR-1kBk,Ωk)} x^k|k=^mk(1∶6)^mk(7) 更新观测矩阵Hk|k∥x^k|k反推观测值代入Hk Pk|k=(P-1k|k-1+HTk|kR-1kHk|k)-1输出:x^k|k,Pk|k

4 性能指标

4.1 偏差和RMSE

(47a)

(47b)

式中:M为蒙特卡罗仿真次数。进一步可得目标跟踪的时间平均偏差和RMSE:

(48a)

(48b)

式中：U=Nt-Lt+1,Nt为整个跟踪阶段的观测次数；Lt表示时刻偏移量,是为了降低跟踪初始阶段的误差对客观比较性能影响。

4.2 CRLB

参数估计的RMSE下界通过CRLB表示,该指标可作为评估性能的参考值。由于运动目标的状态转移还受到过程噪声的影响,所以使用后验CRLB(posterior CRLB, PCRLB)[26]作为状态估计性能的参考值,从而可以给出不等式：

(49)

式中：Jk为Fisher信息矩阵,可通过递推公式计算得到

(50)

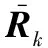
(51)

式中:

所以,目标跟踪的时间平均PCRLB为

(52)

5 仿真分析

为评估本文所提QCKF算法的跟踪性能,通过蒙特卡罗仿真对比该算法与PLKF、EKF、BC-PLKF、SAM-IVKF以及UKF的三维AoA目标跟踪精度,以状态估计的偏差和RMSE作为性能指标,并用PCRLB的平方根(PCRLB1/2)作为RMSE的参考下界。仿真不仅分析各算法在不同观测噪声水平下的性能,而且对比跟踪误差在指定噪声水平下随时刻的变化情况,同时给出各算法的相对运行时间。

5.1 仿真参数

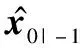
图2 目标跟踪仿真场景

为降低初始跟踪阶段的误差影响,时间平均偏差和RMSE的偏移参数Lt=20。SAM-IVKF在时刻k≤30时执行BC-PLKF算法,并且SAM策略的阈值为4σ。UKF算法需要计算尺度因子,相关参数取值为α=0.5、β=2以及κ=0。

本文QCKF以及PLKF、BC-PLKF和SAM-IVKF算法均建立在观测噪声较小的条件下,但观测噪声标准差σ的取值区间并没有参考指标,这主要源自两方面原因:一方面噪声近似误差与状态估计误差的关系难以构建,另一方面噪声近似误差对状态估计误差的影响能否忽略是与具体的应用需求相关。对此,结合基站进行三维跟踪无人机的仿真场景,以sinnθ,k≈nθ,k和sinnφ,k≈nφ,k的1σ近似误差小于1%作为观测噪声较小的适用条件,所以其标准差σ取值为{1°,2°,…,12°}。此外,所有算法的蒙特卡罗仿真次数M=10 000。

5.2 仿真结果

图3和图4分别为状态估计的位置误差和速度误差随着观测噪声标准差的变化情况。

图3 位置误差随观测噪声变化

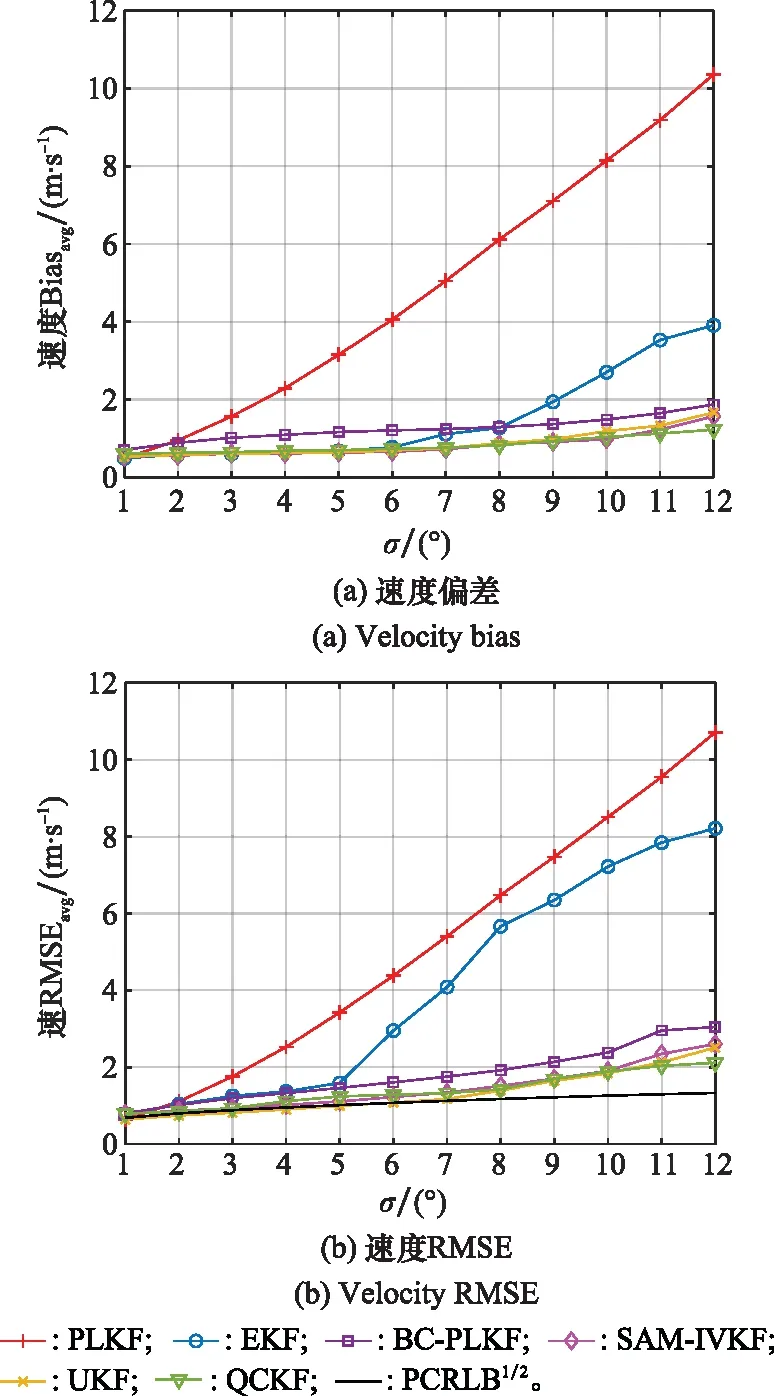
图4 速度误差随观测噪声变化

从图3(a)可看出,PLKF的位置偏差最大,并且随着噪声增大而快速增加;EKF在低噪声条件情况下位置偏差较小,但是当σ≥7°时其偏差也开始较快增加;BC-PLKF的偏差补偿方法能有效降低PLKF的偏差影响,但位置偏差也依然逐步变大,其原因在于偏差补偿的准确性随着噪声增大而降低;SAM-IVKF、UKF和QCKF的位置偏差性能比较接近,均维持在较低水平,尤其当噪声大时QCKF的位置偏差比其他算法更低。

由图3(b)可知,PLKF的位置RMSE仍然最大,这主要由位置偏差影响所造成;EKF在σ≤4°时可以达到后验克拉美罗界,但随着噪声增加,其跟踪误差迅速增大,因为一阶近似引起的初值敏感和发散问题显现;BC-PLKF相较于PLKF的位置RMSE显著降低,但跟踪性能差于SAM-IVKF、UKF和QCKF;当σ≥9°时,SAM-IVKF的位置RMSE明显增加,此时SAM策略逐步以偏差补偿滤波为主导,所以其误差与BC-PLKF不断接近;QCKF在噪声大(σ≥7°)的情况下,位置RMSE始终低于其他算法,尤其当σ=12°时具有更明显的优势,表明其目标跟踪的抗噪声能力更强。

图4展示的速度偏差和RMSE情况与图3的分析类似,但是各算法的速度估计相较于位置估计而言性能差异更小。QCKF的速度估计性能远优于PLKF和EKF,略优于BC-PLKF、SAM-IVKF以及UKF。因此,图3和图4表明即使在速度估计误差接近的情况下,QCKF可以实现更准确的目标位置跟踪,特别是在噪声很大时优势更加突出。表1给出了σ=12°时的95%置信区间宽度,其中EKF的宽度最大,其他算法的差异较小。由于置信区间宽度远低于位置和速度误差,所以图3和图4的结果及分析是可靠有效的。

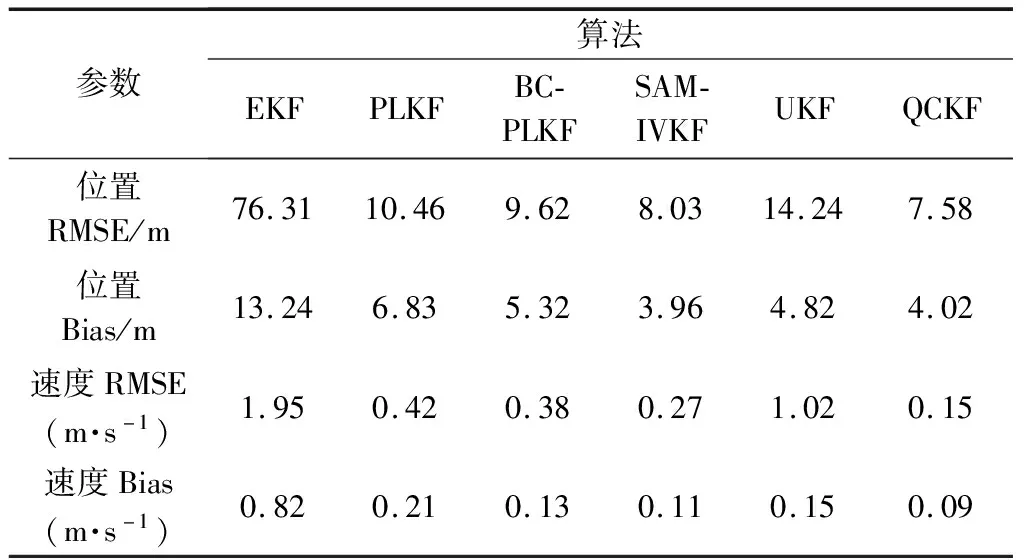
表1 σ=12°时95%置信区间宽度

图5～图7给出了不同观测噪声标准差时跟踪误差随时刻k的变化情况。由于目标跟踪旨在获得目标位置,并且位置和速度的跟踪误差变化情况类似,所以图5～图7仅展示位置偏差和RMSE的变化趋势。为便于直观区分不同算法的数据曲线,图中每隔5个时刻进行符号标记,但实际数据时刻间隔仍为1。从图5(σ=3°)可看出,PLKF受到不断增大的偏差影响,位置误差随时刻快速增加,而其他算法偏差较低,并且可以一直逼近PCRLB。由图6(σ=8°)可知,PLKF和EKF在初始阶段误差明显增加,进而出现发散趋势;BC-PLKF从时刻k=35开始逐步偏离真实轨迹,滤波跟踪误差不断增加;SAM-IVKF、UKF和QCKF的偏差保持在较小范围,RMSE维持在PCRLB附近,其中QCKF的偏离误差更小。从图7(σ=12°)可看出,PLKF和EKF很快出现发散,位置误差迅速增加;SAM-IVKF和BC-PLKF的跟踪性能较为接近,原因在于噪声严重时SAM策略以偏差补偿作为主要滤波方法;QCKF在位置偏差和RMSE性能指标上均比其他算法更优。值得注意的是,运动目标的位置不断远离观测站,使得AoA目标跟踪的距离放大误差问题显现,所以PCRLB在图5～图7中均呈现上升趋势。

图5 σ=3°时位置误差随时刻变化

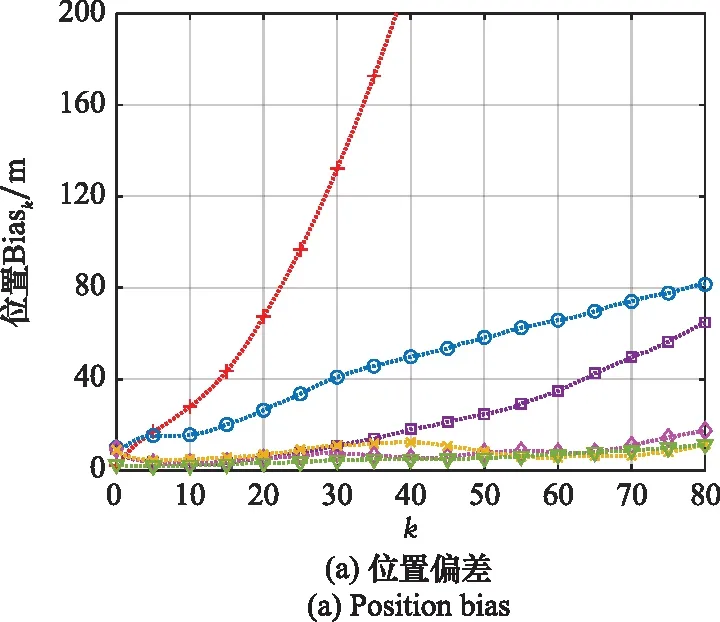
图6 σ=8°时位置误差随时刻变化

图7 σ=12°时位置误差随时刻变化

各算法的相对运行时间如表2所示,其中以EKF运行时间作为基准进行归一化。BC-PLKF的偏差补偿过程使得计算开销高于PLKF;SAM-IVKF结合偏差补偿和工具变量方法,所以比BC-PLKF的运算时间更长;QCKF需要构造约束矩阵以及特征值分解,其计算开销比SAM-IVKF略高,但是相较于UKF可以大幅降低运行时间。因此,表2、图3和图4表明QCKF以相对较低的计算开销实现了更优的估计性能。

表2 不同算法相对运行时间比较

6 结 论

本文针对PLKF在三维AoA目标跟踪中存在严重偏差的问题,提出一种有效降低估计偏差的QCKF算法。通过附加二次约束条件到所建立的目标函数,使其在状态为真值时取得最小值,以此克服由伪线性噪声和观测系数矩阵的相关性所引起的偏差影响。仿真对比分析了PLKF及其改进算法BC-PLKF、SAM-IVKF,非线性滤波算法EKF、UKF以及本文QCKF算法,结果充分证实了QCKF的滤波跟踪性能更优,尤其是当噪声严重时具有更显著的优势,并且计算开销相对较低。

本文在分析偏差时假设过程噪声较小,这适用于匀速运动、匀加速运动、匀速率转弯运动等平稳变化的动态模型。当目标状态剧烈变化时,系统过程噪声较大,也会引起偏差,可通过多模型方法降低其影响。针对观测噪声服从高斯分布的假设,可以结合高斯混合模型处理非高斯观测噪声。