面向大规模矩阵乘法的编码计算性能研究
2021-07-27王希龄赖宏达李念爽
王 艳,王希龄,赖宏达,李念爽
(华东交通大学软件学院,江西 南昌 330013)
互联网的飞速发展和大数据处理框架的进步推动了大规模的机器学习部署,并促进了分布式机器学习算法在更多领域中的应用[1-5]。 为了更高效地利用大数据训练更准确的大模型,在机器学习中引入大量矩阵乘法, 一旦采用了分布式机器学习模式,就意味着大量矩阵乘法的分布式计算。 然而,分布式集群中存在某些计算节点由于各种因素的影响(如节点失效、系统故障、通信瓶颈等),计算速度会以某种随机的方式变慢,从而使分布式机器学习算法执行时间增加,成为分布式计算系统的主要瓶颈[6],这种节点被称作掉队节点。 目前减缓掉队节点影响的方法主要是增加某种形式的“计算冗余”,例如,采用副本的方式在多个节点上执行相同的计算任务[7]。 然而,最近的研究结果表明,编码计算可以更加有效地减轻掉队节点的影响[8-12],同时相较于副本方案成本更低。
Tandon 等[13]研究了分布式系统中梯度计算的最优编码设计, 提出了一种新的编码计算方案,用于计算函数的和,展示了对梯度进行编码可以提供同步梯度下降法对失效节点和掉队节点的容忍。 他们根据工作节点运行速度变慢的程度将掉队节点分成完全掉队节点(Full Stragglers)和部分掉队节点(Partial Stragglers)两种,针对这两种情况,提出了一种编码方案来实现机器学习集群对掉队节点的鲁棒性。 Ye 等[14]提出了通信计算高效梯度编码方案,它从计算负载、掉队节点容忍和通信成本3 个方面描述了梯度计算的基本权衡。 Li 等[15]提出了一种MapReduce 的编码框架,称为“Coded MapReduce”,它在r(r∈N)个精心选择的节点上分配每个任务的映射计算,以使网络内的节点减少r 倍的通信负载。Li 等[16]将文献[15]中提出的编码思想应用于Tera-Sort,提出了一种新的分布式排序算法“Coded Tera-Sort”, 大大提高了Hadoop MapReduce 中TeraSort基准的执行时间。 Reisizadeh 等[17]研究由各种不同性能的计算机组成的通用异构分布式计算集群,提出了一个编码框架, 通过交换冗余来减少计算延迟, 从而加速存在掉队节点的异构集群的分布式计算。Ferdinandn 等[18]提出了一种用于近似矩阵乘法的任意时刻编码方案, 通过近似计算的形式来加速分布式计算。 Dutta 等[19]考虑了存在掉队节点的情况下, 使用并行处理器计算两个长向量的卷积问题, 提出了存在截止时间的卷积问题的编码计算方案。 Park 等[20]提出了一个由工作节点组成的层次计算结构。
上述研究都是通过提出编码方案来增加对掉队节点的鲁棒性,并未对各自编码方案的性能开销展开研究,本文重点考察了面向分布式机器学习的各编码计算方案的任务完成时间和机器计算总时间两类开销。 本文定义了面向分布式机器学习的编码计算的两个性能指标:一是某个使用该编码方案的计算任务完成时间,即完成整个计算任务所需要的时间;二是整个计算任务的机器计算总时间,即整个分布式计算系统中所有工作节点对该计算任务进行计算的时间的总和。 通过计算由n 个工作节点组成的分布式系统中第i 个完成计算任务的节点的密度函数,给出工作节点计算任务完成时间符合均匀分布场景下计算任务的完成时间和机器计算总时间的表达式;对比分析了这一场景下3 种应用于矩阵乘法的编码方案的完成时间和机器计算总时间,并通过实验对比了指数分布场景下不同情况对任务完成时间与计算节点总计算开销影响, 提供了计算方案选择的依据。
1 分布式计算开销示例
在机器学习算法中,我们经常要执行矩阵乘法的操作。 我们考虑这样一个矩阵乘法问题:通过输入矩阵A 和向量X 计算出矩阵B=AX。由于工作节点的内存大小有限,矩阵A 按列被分成3 个大小相等的子矩阵,即A=[A1A2A3],计算工作分别在图1和图2 所示的两个分布式计算系统中进行的。
图1 所示的分布式计算系统由1 个主节点和3个工作节点组成,每个工作节点分别预先存储子矩阵A1,A2,A3中的一个,且各个节点存储的矩阵互不相同。 主节点将向量X 发送给每个工作节点,工作节点Wi(i=1,2,3)将本地存储的矩阵与向量X 进行乘法运算。 主节点接收到3 个工作节点的计算结果, 可计算出B。 假设图1 的计算系统中节点W1,W2和W3的计算任务完成时间(T) 分别为2,6 ms和10 ms,那么第一个计算系统T=10 ms,机器计算总时间C=2+6+10=18 ms。
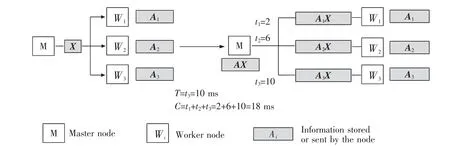
图1 未编码方案示例Fig.1 Illustration of uncoded scheme
图2 所示的分布式计算系统由1 个主节点和5个工作节点组成,使用(5,3)MDS 编码将矩阵A 分成 的3 个 子 矩 阵 编 码 为5 个 编 码 矩 阵A1,A2,A3,A1+A2+A3,A1+2A2+3A3,并分别预先存储在5 个工作节点W1,W2,W3,W4,W5中。主节点将向量X 发送给每个工作节点,工作节点Wi(i=1,2,3,4,5)将本地存储的矩阵与向量X 进行乘法运算,并在完成计算任务后,将结果发送回主节点。一旦主节点接收到5个计算结果中的任意3 个,其他工作节点就会停止工作,主节点就可以计算出AX。 例如,当主节点接收到A1X,A3X 和(A1+A2+A3)X 时,它可以通过计算(A1+A2+A3)X-A3X-A1X 得到A2X,然后计算出AX。这一编码方案,相较于未编码方案必须接收到全部计算结果才能完成最终计算,能容忍2 个节点计算速度较慢或完全失效。
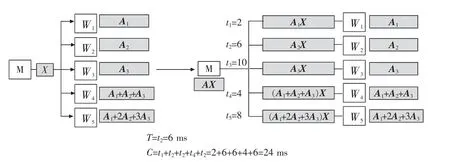
图2 编码方案示例Fig.2 Illustration of coding scheme
假设图2 中5 个计算节点的完成时间分别为2,4,6,8,10 ms, 主节点在接收到任意3 个节点的计算结果后就立刻通知剩余的其他2 个节点停止计算(根据MDS 编码性质,任意3 个节点的计算已足够得到矩阵B),所以任务完成时间T=6 ms,机器计算总时间C=2+4+6+6+6=24 ms。
从上述结果可以看出, 相较于未编码方案,虽然编码方案的任务完成时间减少了,但是机器计算总时间比未编码方案更高。
2 模型建立
在一个由1 个主节点和n 个工作节点组成的分布式计算系统中, 由于每个工作节点内存有限,先将总的计算任务分成若干个大小相等的子任务,然后使用编码技术将这些子任务编码成n 个大小相同的编码计算任务,发送给每个工作节点进行计算,主节点在接收到任意k 个工作节点的计算结果后,即可计算出最终结果。
我们通过以下两个性能指标评估一个编码方案的性能:
任务完成时间(T):从主节点将子任务分配给每个工作节点开始,直到主节点接收到足够多的工作节点提交的计算结果,能够完成整个计算任务所需要的时间;
机器计算总时间(C):整个分布式计算系统中所有工作节点对该计算任务进行计算的时间的总和。
假设这n 个工作节点的计算任务完成时间分别为t1,t2, …,tn, 记Xi为这些任务完成时间中第i个最小的完成时间
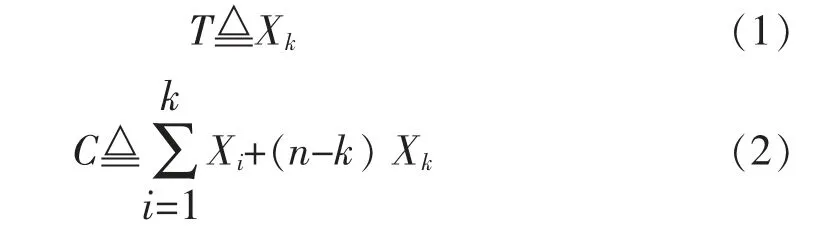
由于接收到k 个工作节点的计算结果后,主节点即可计算出最终结果,任务完成时间T 为主节点接收到第k 个计算结果的时间,即Xk。 此时分布式计算系统的计算任务就已完成,主节点会向所有工作节点发送一个停止工作的信号,未完成计算任务的(n-k)个工作节点也在Xk时刻停止计算,机器计算总时间C 即为式(2)所示。
由于工作节点在进行计算任务时可能会由于各种原因导致计算速度相较于正常节点更慢或是更快,使得每个工作节点完成计算任务的时间可能会不同,每个工作节点计算任务的完成时间ti(i∈{1,2,…,n})是一个独立同分布的连续随机变量,具有概率分布F 和密度函数f。 为了得到Xi的分布,因Xi小于或等于x 当且仅当这n 个节点的计算时间X1,X2,…,Xn至少有i 个小于或等于x。



3 3 种编码方案性能的对比分析
对于给定的任何一种编码策略,本文将完成一个计算任务所需等待的最小工作节点数定义为该编码策略的恢复阈值。 也就是说,如果任何大小不小于恢复阈值的工作节点子集完成了它们的工作,主节点就能够计算出最终结果。 在本文中,恢复阈值可以理解为:当主节点接收到这n 个工作节点中最快的前i 个工作节点的计算结果后, 即可计算出最终结果。
在计算各编码方案的任务完成时间T 和机器计算总时间C 之前,必须要说明的是,由于编码方案的不同,每种编码方案中工作节点的计算量是不同的,因而计算时间也不相同。 这在模型中可以体现为,当工作节点的计算时间符合均匀分布的场景下,各个编码方案的区间(a,b)会有不同。 为了方便,本文将进行一次乘法的计算量记为1,进行加法的计算量忽略不计, 如一个1×n 的向量与一个n×1的向量相乘的计算量为n, 而一个n×1 的向量与一个1×n 的向量相乘的计算量为n2。
为了更好的对比各个编码方案任务完成时间T和机器计算总时间C, 还需要给这些编码方案构造一个相同的计算场景,目标都是通过输入矩阵A 和B 计算出H=ATB,如图3 所示。矩阵A 的维度为Z×X,矩阵B 的维度为Z×Y,计算任务是在拥有1 个主节点和N 个工作节点的分布式系统中进行。 其中,两个输入矩阵分别被(任意)划分为p×m 和p×n 个子矩阵块,每一个输入矩阵划分的子矩阵大小是相同的,且每个工作节点只能在本地存储2 个子矩阵。 另外,每个编码方案的p,m,n 的取值是不同的。

图3 矩阵乘法问题示例Fig.3 Example of matrix multiplication problem
目前最常用于矩阵乘法的编码方案为: 一维MDS 编码、乘积编码、多项式编码。本文将对这3 种编码方案进行介绍以及实验对比其性能。
3.1 一维MDS 编码方案
一维MDS 编码方案是Lee 等[21]对文献[22]的编码思想进行扩展得出的, 将MDS 码在一个输入矩阵中加入冗余数据这种方法称为一维MDS 码(1D MDS 码)。 该编码方案的思想是:将大矩阵乘法的问题看作n 个小矩阵乘法的问题,即ATB=[ATb1ATb2… ATbn], 然后对n 个小矩阵中的每一个分别应用MDS 编码矩阵乘法。假设N=nk,工作节点被分成大小为k 的n 个组,每个组都专门计算一个ATbj。例如对于第一个组,它用于计算ATb1,该方案首先使用(k,m)MDS 编码对矩阵A 的沿列分成的m 个大小相同的子矩阵进行编码, 以获得k 个编码矩阵,比如a1到ak,然后将aiTb1的计算分配给这组的第i 个工作节点,以此类推。 MDS 编码计算的计算时间由n 个组的计算时间中的最大值决定, 每个组的计算时间由组中k 个工作节点中第m 个完成计算任务的工作节点决定。
图4 所 示 为N=3,m=2,n=1,p=1 时 的1D MDS 编码方案示例, 主节点接收到3 个工作节点中的任意2 个返回的计算结果后, 即可计算出矩阵H。

图4 3 工作节点的1D MDS 码示例Fig.4 Illustration of 1D MDS code with 3 work nodes

3.2 乘积码编码方案


图5 9 工作节点的乘积码示例Fig.5 Illustration of product code with 9 work nodes

3.3 多项式码编码方案
多项式码编码方案是Yu 等[23]提出的一种编码计算策略,利用编码理论的思想来设计工作节点上的中间计算,以实现对掉队节点的容忍。 该方案首先沿着列将2 个输入矩阵分别平均分成m 和n 个大小相等的子矩阵

然后给每个工作节点i(i∈{0,1,…,N-1})分配一个数字xi,同时使得所有的xi都互不相同,在工作节点i 本地存储以下2 个编码子矩阵

由于所设计的计算策略具有特殊的代数结构,解码过程可以看作是一个多项式插值问题(或是一个解码Reed-Solomon 码的问题),可有效求解。这种多项式编码的主要创新之处和优点在于,通过精心设计编码子矩阵的代数结构,可以确保工作节点上的任何mn 个中间计算都足以在主节点上恢复矩阵乘法的最终乘积。 从某种意义上来说,这是在中间计算中创建了一个MDS 结构, 而不是像以前的工作那样仅仅是对矩阵进行编码。
图6 所示为N=5,m=2,n=2,p=1 时的多项式码编码方案示例,主节点接收到5 个工作节点中的任意4 个返回的计算结果后,即可计算出矩阵H。

图6 5 工作节点的多项式码示例Fig.6 Illustration of polynomial code with 5 work nodes

另外,在多项式编码的基础上,Yu 等[24]提出了纠缠多项式编码方案, 实现了pmn+p-1 的恢复阈值;Dutta 等[25]提出了MatDot 编码方案,实现了2m-1 的恢复阈值。 由于这几种方案都是通过设计编码子矩阵的代数结构实现对掉队节点的容忍,本文仅将多项式编码方案与其他编码方案进行对比分析。
4 实验及结果
为了更加直观的比较各个编码方案的任务完成时间T 和机器计算总时间C,我们通过实验对3种编码方案的性能指标进行了测试。
本文使用Python 语言实现了3 种编码方案的编码计算过程。 当编码参数设置为a=1,b=9,X=Y=Z=4,N=16 时, 本文分别对未编码方案和3 种编码方案的任务完成时间T 和机器计算总时间C 进行了数值上的测量,实验结果如表1 所示。
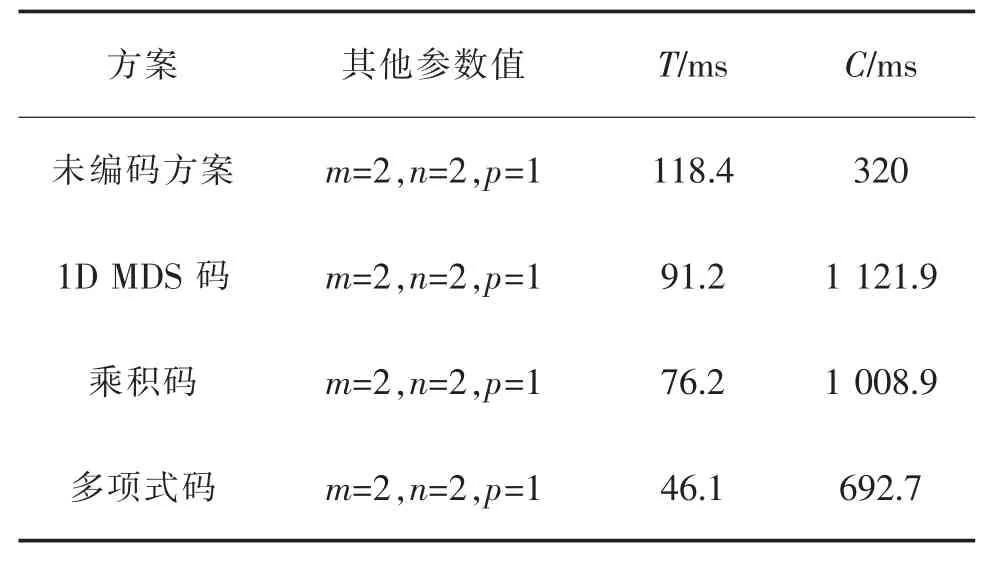
表1 未编码方案和3 种编码方案的对比Tab.1 Comparison between uncoded scheme and three coding schemes
从表中结果可以看出,编码方案与未编码方案相比:编码方案的任务完成时间普遍要短,这是因为每种编码方案只需等待达到其恢复阈值的工作节点子集完成计算任务即可得到最终结果,而不必等待所有节点完成计算任务;但是编码方案的机器计算总时间普遍更长, 这是因为相较于未编码方案,编码方案使用了更多的工作节点来完成计算任务。 将3 种编码方案进行对比:乘积码的任务完成时间和机器计算总时间相较于1D MDS 编码方案都要短,这是由于乘积码的恢复阈值更低;多项式码在3 种编码方案中,任务完成时间和机器计算总时间的表现都是最优,这是因为在给定其他参数情况下3 种编码方案p,m,n 的取值都相同时,多项式码的恢复阈值远小于另外两种编码方案,但是该方案额外增加了主节点的编解码,是以增加主节点的计算时间为代价的。
4.1 编码方案的参数选择
选定一个合适的编码方案之后,比如某用户准备使用多项式编码计算方案对2 个大小为100×100的矩阵进行乘法计算,若该用户选择将两个输入矩阵分别划分为4 个大小相同的子矩阵, 即m=n=4,假设该用户选择在20 个工作节点上执行计算任务,且在该用户选择的工作节点的工作环境下a=1,b=9,那么此时任务完成时间T=443 252 ms,机器计算总时间C=4 824 405 ms。 若是该用户选择将两个输入矩阵分别划分为4 个大小相同的子矩阵,即m=n=5,假设该用户选择在29 个工作节点上执行计算任务,且在该用户选择的工作节点的工作环境下a=1,b=9 , 那么此时任务完成时间T=306 667 ms,机器计算总时间C=4 573 333 ms。 从上述例子中可以看出,不同的参数选择会导致机器计算总时间C,即资源消耗的不同。 那么我们又面临着这样一个新的问题:如何选择编码方案的参数,使得用于编码计算任务的资源消耗最少。
将这一问题使用数学语言可以描述为: 在给定工作节点数量N 和任务完成时间T 的限制时,如何选择m,n,N 和其他参数的值, 使得机器计算总时间C 最小。
要研究选择m,n,N 和其他参数的值, 使得机器计算总时间C 最小,我们首先要了解机器计算总时间C 与这些参数之间有什么关系,即参数变化时C 的变化趋势。 另外,由于对工作节点数量N 和任务完成时间T 的限制可以理解为给定了N 和T 的上限,并不代表着所给工作节点数量N 和任务完成时间T 的值就是最终结果,我们还需要对工作节点数量N 和任务完成时间T 进行研究,分析这两个参数之间、两个参数与机器计算总时间C 之间以及两个参数与其他参数之间的关系。
我们首先对前文求出的3 种编码方案的任务完成时间T 和机器计算总时间C 的表达式进行研究。 从3 种编码方案性能指标的表达式中,可以很明显地观察到,当其他参数保持不变时,增加Z,X,Y 的值,T 和C 都会随之增加;增加mn 的值,T 和C都会随之减小。 但是当N 增加时,T 和C 的值不容易判断,本文又对工作节点数N 变化的情况下3 种编码方案的T 和C 的变化情况进行了实验分析。在其他参数分别设置为a=1,b=9,X=Y=Z=100,m=n=5,p=1 时,计算出N 分别取值为30,35,40,45,50,55,60,65,70,80,90,100,120,160,200,240,280,320,360 时各编码方案的T 和C 的值,如图7 所示。

图7 3 种编码方案在不同N 取值下的T 和C 变化情况Fig.7 Changes of T and C in three coding schemes with different values of N
从图7 中可以看出, 随着工作节点数N 的增加,3 种编码方案的机器计算总时间C 都在不断增加,而任务完成时间T 都在不断减小,这说明增加更多的冗余工作节点,能更快的完成计算任务,但是计算任务成本开销也会相应地增加。 另外,从图中还可以看出,在C 增加到一定程度后, T 的减小会变得缓慢, 这说明增加的冗余达到一定程度之后, 再继续增加冗余, 成本开销依然会继续增加, 但是任务完成时间却减少的很慢甚至不再减少,此时收益很低。
当输入矩阵A 和B 划分成的子矩阵数量不同,即参数m,n 不同时,我们通过实验对编码方案的任务完成时间T 和机器计算总时间C 进行了研究。 以多项式码编码方案为例,当a=1,b=9,X=Y=Z=4 时,本文分别给出了m,n 取值不同的情况下T 和C 的变化情况,研究结果如图8 和图9 所示。
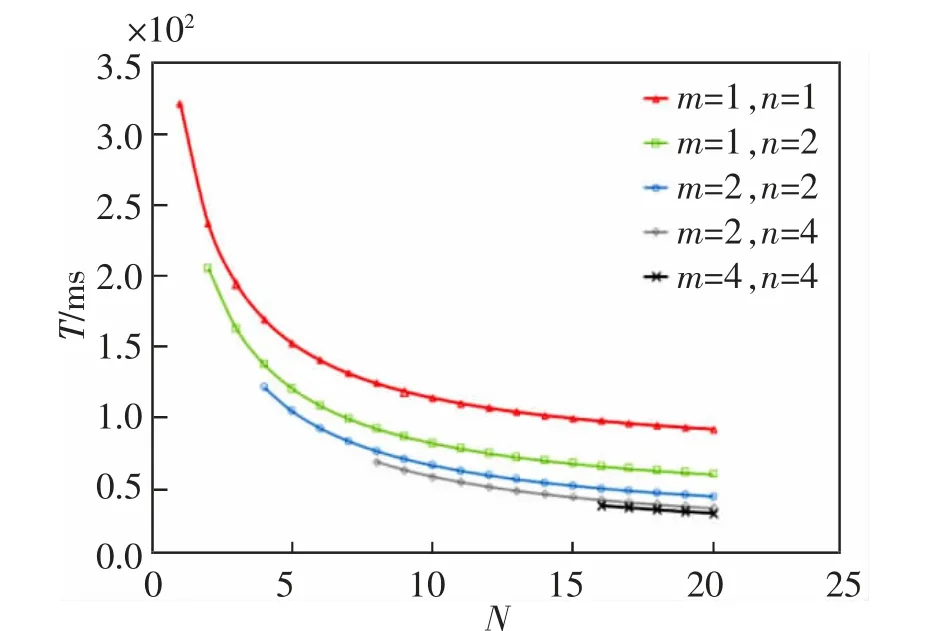
图8 m 和n 值不同时多项式编码框架的T 的变化情况Fig.8 Changes of T for polynomial code scheme with different values of m and n
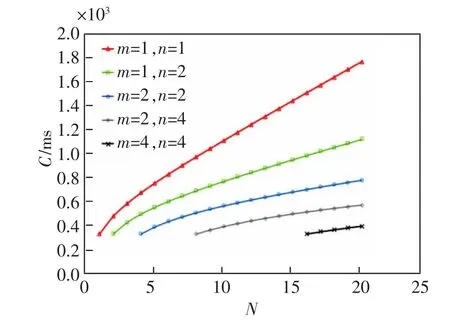
图9 m 和n 值不同时多项式编码框架的C 的变化情况Fig.9 Changes of C for polynomial code scheme with different values of m and n
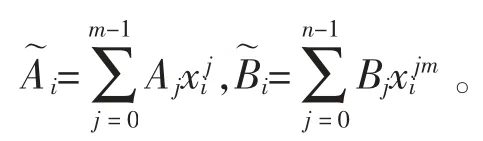
可以看出,当m 和n 的取值越大时,编码子矩阵就越复杂,生成编码子矩阵以及对编码子矩阵进行编解码所需要的时间也就越长。 m 和n 的取值越大并不能使进行编码计算任务花费的全部时间越短。
从图9 可以看出,当给定N 时,选择m×n 较大的输入矩阵划分方案,可以得到较小的C。这是因为当工作节点的总数量保持不变时,每个工作节点的工作时间减少, 机器计算总时间自然也就随之减少。 此外,当工作节点数量N 与多项式码的恢复阈值mn 相等时, 也就是说在分布式计算系统中没有冗余存在,此时无论N 的取值如何变化,多项式编码方案的机器计算总时间C 总是相等的,这是由C的计算表达式决定的,这也是多项式编码方案的机器计算总时间C 如图7 变化的原因。
4.2 参数的启发式算法
在对4.1 节实验结果进行分析的基础上, 本文给出了在给定T 和N 的上限时, 如何选取m,n,T的值来最小化机器计算总时间C 的启发式算法,算法过程如下所示:
输入:矩阵维度X,Y,Z,计算节点完成最快时间a,最慢时间b,给定T 和N 的上限;
输出:计算总时间C 的预测值,及最小化C 的参数m,n 的取值,任务完成时间T 和工作节点数量N;
1) 根据输入矩阵大小求出所有可用的矩阵划分方案m 和n 的可能值;
2) 根据用户所给的任务完成时间T 的限制选择合适的m 和n 的取值;
3) 根据工作节点数量N 的上限判断在给定T和上限内是否能完成计算工作;
4) 若能则给出使得机器计算总时间C 最小的各项参数的取值。
在算法中输入给定的任务完成时间T 和工作节点数量N 的上限以及需要进行乘法计算的矩阵大小, 然后算法会输出可以使得机器计算总时间C最小化的参数m,n 的取值,任务完成时间T 和工作节点数量N 的预测值以及机器计算总时间C 的预测值。
当算法输入为a=1,b=9,X=Y=Z=100,N=46,T=200 000 ms 时,输出为m=2,n=20 或m=4,n=10 或m=10,n=4 或m=20,n=2,T=195 212.8 ms,C=5 660 638.3 ms。
在mn 不同取值下C 的取值如表2 所示, 可以看出算法结果的确可以输出使得机器计算总时间C最小化的参数m,n 的取值。
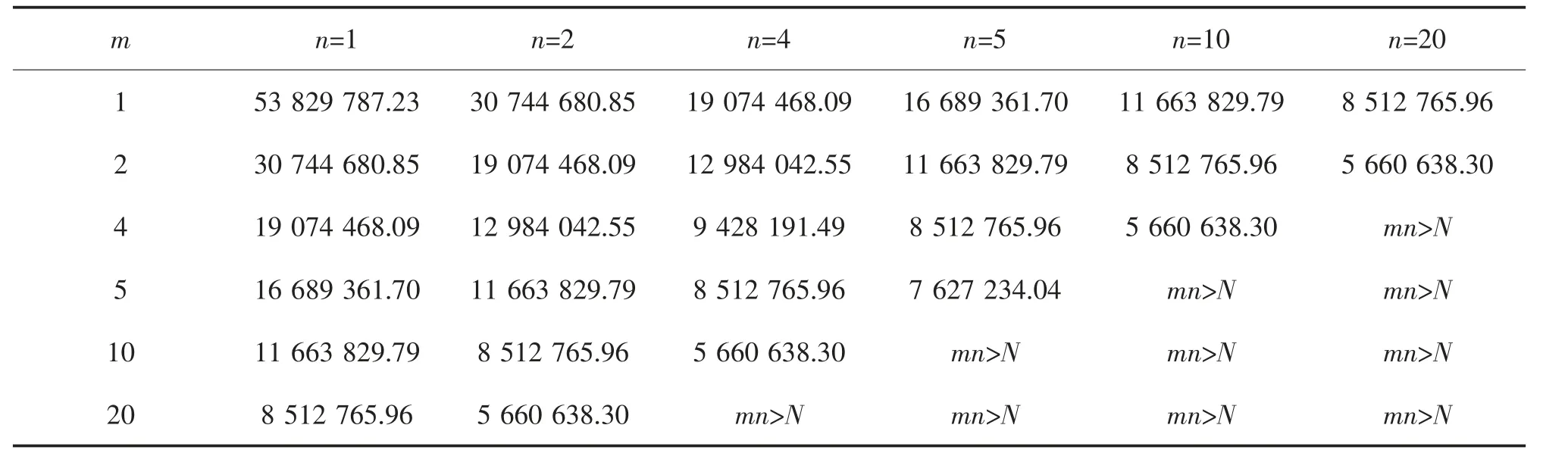
表2 在mn 不同取值下C 的值Tab.2 C with different values of m×n
5 结论
1) 本文对基于分布式机器学习的编码方案的性能开销进行了研究和分析,计算出了n 个工作节点中第i 个完成计算任务的节点的密度函数,并给出了工作节点计算任务完成时间符合均匀分布场景下计算任务的任务完成时间C 和机器计算总时间T 的表达式。
2) 分析对比了3 个应用于矩阵乘法的编码方案与未编码方案的任务完成时间和机器计算总时间,提供了计算方案选择的依据。 并且在此基础上,通过Python 实验了指数分布情况下的编码方案并实验得出了其任务完成时间C 和机器计算总时间T,还在此基础上进行实验,对3 种编码方案进行比较。
3) 在此基础上还对参数选择进行分析, 提出一个启发式算法为参数的选择提供参考。
