肖宇宇 何斯日古楞 杨凯丽

(1.内蒙古大学数学科学学院,内蒙古呼和浩特 010021;2.呼和浩特民族学院,内蒙古呼和浩特 010051)

§1 引言

时间间断时空有限元方法的研究发展于20世纪70年代后期.文献[1]用时间间断的时空有限元方法求解非线性薛定谔方程时提出了有限元与拉格朗日插值相结合的技术,即在理论分析时引入由时间剖分单元In上的Radau点确定的拉格朗日插值多项式及相应的高斯Radau积分准则,并应用有限元技术,插值多项式的基本性质及高斯积分准则的高精度性在弱的时空网格限制条件下给出了数值解的最优L∞(L2)模误差估计.随后,文献[2-6]利用这一技术,分别研究了抛物型方程,奇异微分方程,Sobolev方程等发展型方程的时间间断时空有限元方法,进行了收敛性分析.文献[7]针对一维抛物型方程提出了时间间断的有限体积元格式,并利用有限体积元和有限差分结合的技巧证明了数值解的最优L∞(L2)模误差估计.文献[7]中数值格式采用分片线性多项式为时空试探函数空间,只具有二阶收敛精度.

本文将时间间断Galerkin思想与基于等距节点下三次Lagrange插值的超收敛有限体积元方法[8]相结合,以三次Lagrange插值导数超收敛点为对偶剖分节点,引入插值投影算子,构造一种高精度时空有限体积元格式求解对流扩散问题

其中已知函数p,q,r,f充分光滑,且p(x)≥pmin＞0,r-q′ ≥0.

相比于文献[1-6]的方法,本文所构造的时空有限体积元格式不仅继承了有限体积元方法[8-9]的高精度,计算简单等特点,而且能保持物理量的局部守恒性.相对于文献[7]的方法,这种方法将时间变量和空间变量统一考虑,在时间和空间两个方向分别发挥有限元方法和有限体积元方法的优势,从而达到时间和空间变量的高精度,并且在时间剖分节点处具有超收敛性.

本文结构如下:§1简单介绍了时空有限元法的发展历史及对流扩散问题;§2构造了一种高精度时空有限体积元格式;§3分析了所构造格式的最优收敛性;§4给出数值算例验证了所提格式的可行性和有效性.

本文使用标准Sobolev空间Hm([a,b]),范数||v||m,半范数|v|m以及L2([a,b])空间及其相应的内积(v,w).本文中所有的c,ci都是与时间和空间步长无关的正常数,并且不同地方可能取值不相同.

§2 时间间断时空有限体积元格式

为构建高精度时空体积元格式,首先分析三次Lagrange插值多项式的导数超收敛节点.在[-h,h]上,用等距节点(-h,u(-h)),,(h,u(h))对未知函数u作Lagrange插值,插值函数记为Πhu,令,则

将u(-h),,u(h)均在x0处作Taylor展开,可得

建立试探函数空间.在时空片In×Tnh内,设Snh ⊂H10([a,b])是分片三次Lagrange 有限元空间,即

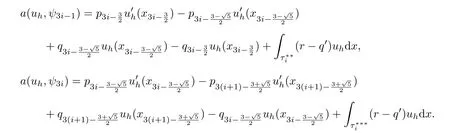
下面给出收敛性分析所需一些定义和引理.引入Radau积分公式[1]

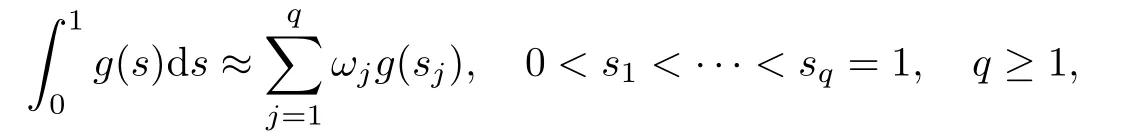
使得对所有次数不高于2q-2次的多项式精确成立.

使用线性变换t=tn+sΔtn,可将区间映射到[0,1],从而有如下记号

设M,N是q×q矩阵,使得

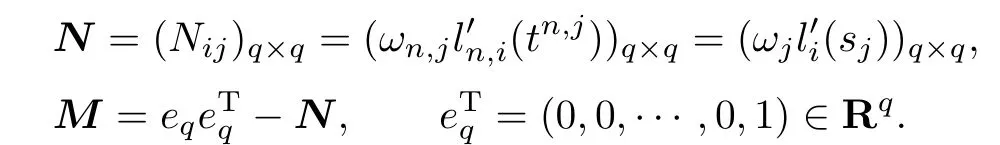
显然,M和N不依赖于Δtn,且当YT=(yn,1,yn,2……·yn,q)∈Rq时,有

引理1[1]设矩阵,D=diag{s1,s2,……,sq},则有

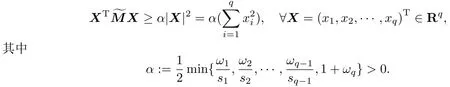
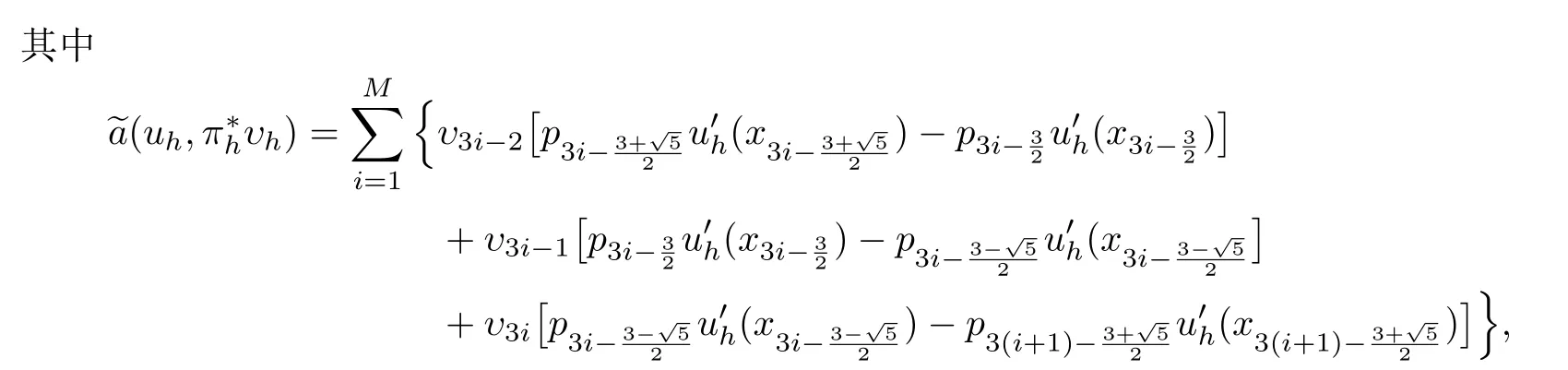
定义2时空范数定义为

引理2(参见[8,9]) 对于任意的uh,vh ∈Snh,有

引理3(参见[8]) 对充分小的h,存在正常数c3,c4和c5,λ ＜∞,使得

其中常数β满足rmin ＞β ＞0,,并

证为分析,首先将其分解成

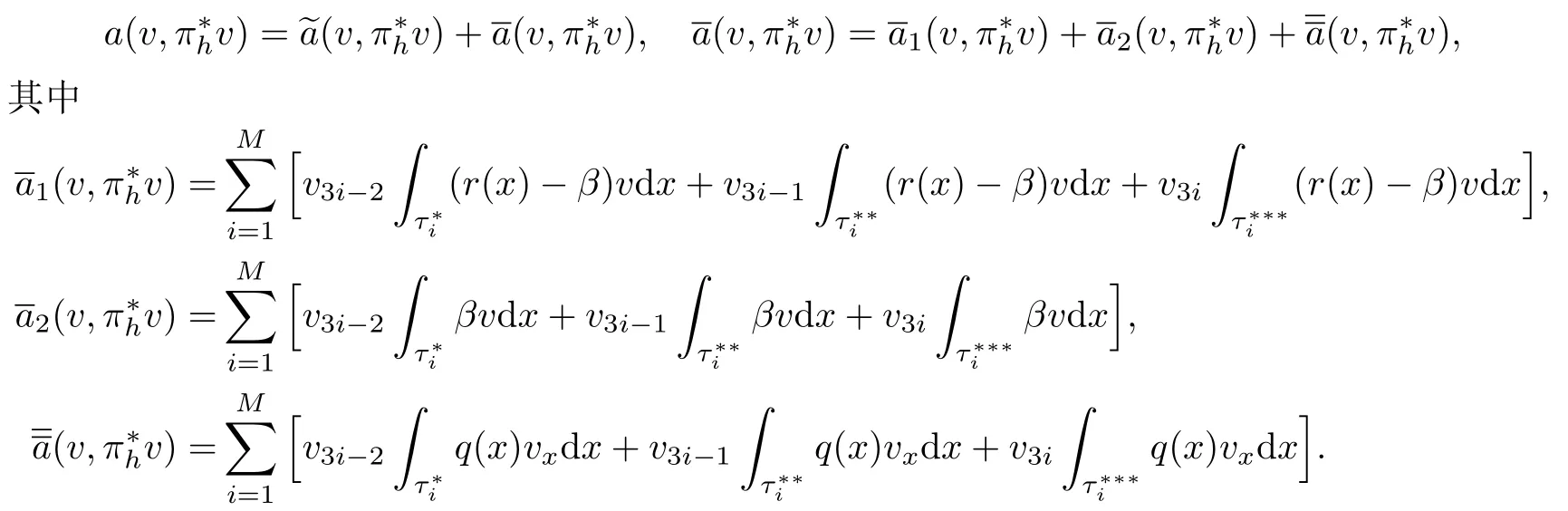
由于v ∈Sh是三次多项式,并用分部求和公式及不等式-ab ≥-(a2+b2)/2,得

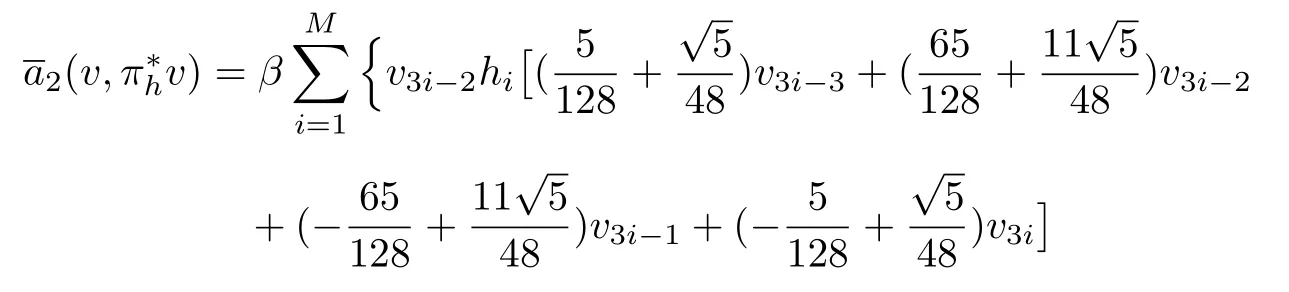
定义3在时间单元In=(tn,tn+1]上定义以Radau点tn,j为节点的Lagrange插值算子:C()→Pq-1(In)满足

Si基谐振式光学微腔陀螺的核心技术指标为极限灵敏度,其主要取决于微腔结构的质量均匀性、表面粗糙度以及微腔直径(D)等结构参数。目前Si基微腔结构在微米级时,表面粗糙度能达到1 nm以下,已接近材料表面粗糙度的极限,Q值到107左右[8-9],此时,微腔陀螺的极限灵敏度就主要取决于微腔直径D值[10]。

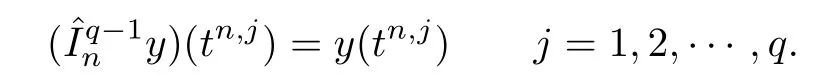
进一步,定义W:[0,T]([a,b])使得

为简单起见,仍用W表示W|In.

引理4(参见[1]) 由插值逼近性质,函数u和函数W(x,t)的误差具有如下估计

§3 收敛性分析及误差估计

定理1设u和U分别为(1)和(3)的解,则满足

其中Nc表示(j=1,……,N -1)的总数.

证利用前面定义的W,将误差项分裂为e=U -u=(U -W)+(W -u)=θ+ρ.对ρ有引理5 的估计结果,因此下面只需对θ进行估计.首先,由时间间断时空有限体积元格式(3) 得基本误差方程

代入(6)式得

其中记号δq,i=ln,i(tn+1)=ln,i(tn,q)=1 (i=q),否则δq,i=0,(i/=q),

在(7)式中取φ=θn,i,然后关于i从1到q求和,并用引理3可得

对于上式中的Σ1,Σ2,Σ3有如下估计[1]

由于∀x ∈[a,b],是关于时间变量t的2q-2次多项式,因此

于是用Cauchy-Schwarz不等式得

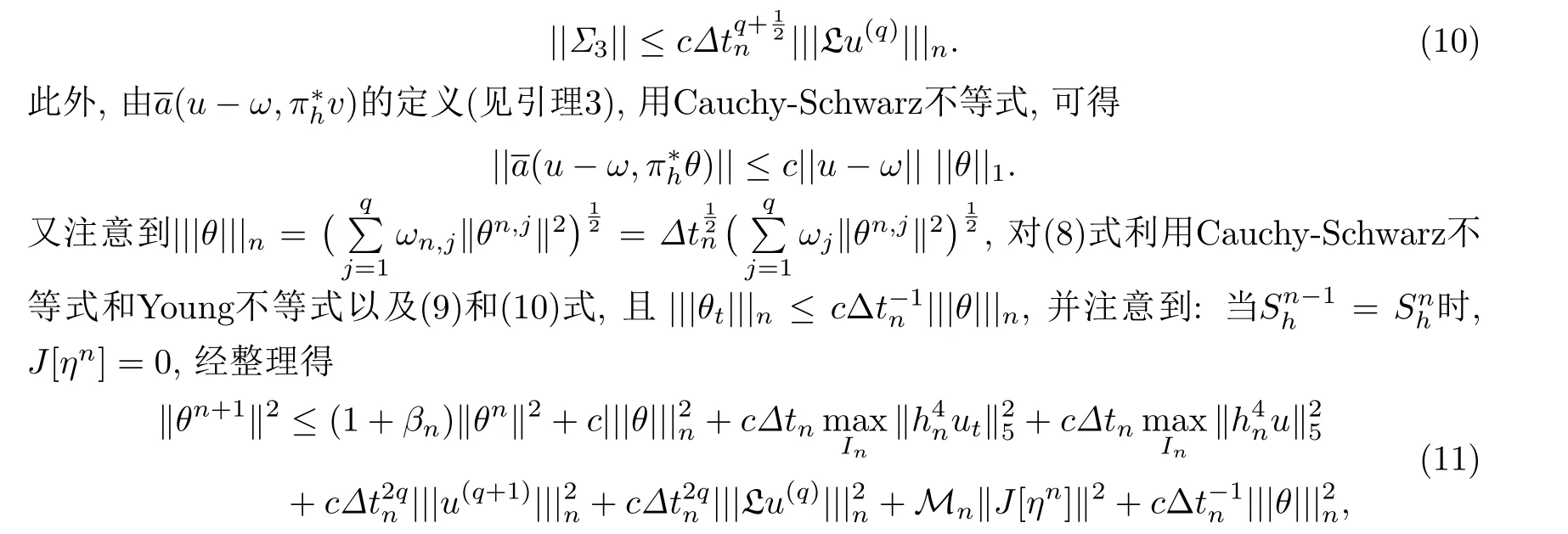
其中,Mn是与n无关的常数,其具体取值参见后面步骤.

因此利用引理3,有

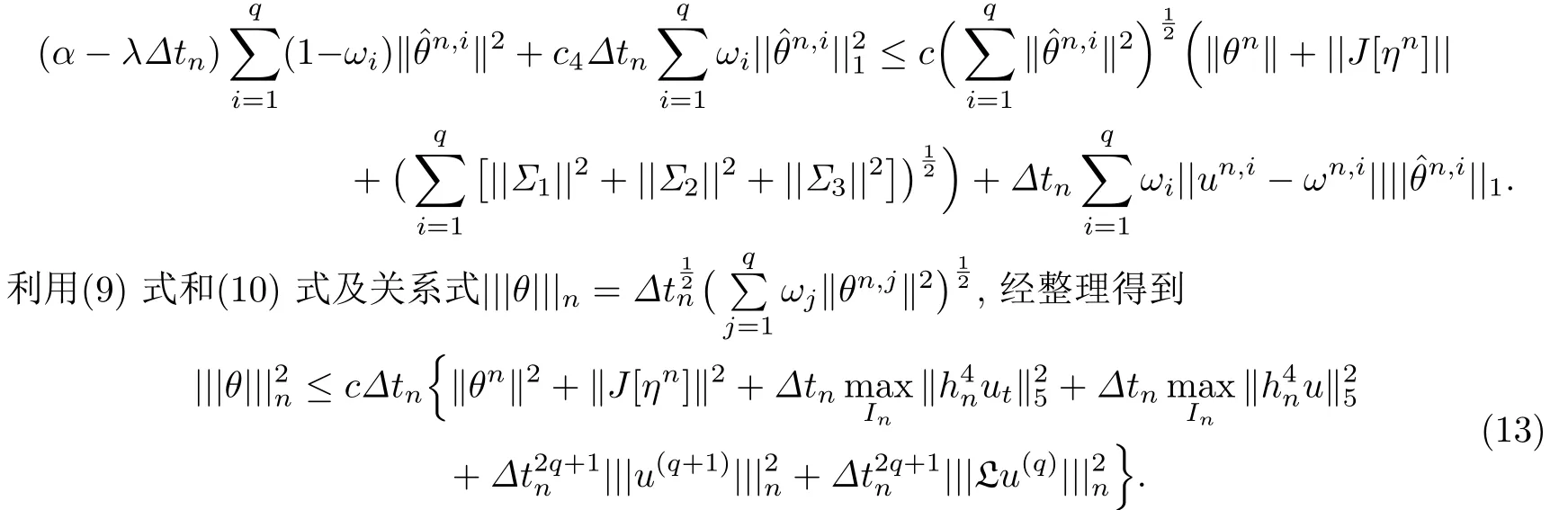
把上式代入(11)式的右端,再对n进行迭代,经整理得

现对于固定的n,取Mm=M=Nc(n)(m=1,……,n).这里Nc(n)表示的总数,并且当Nc(n)=0或1时,取M=2.于是,当.因此,有不等式

其中M=Nc(n).于是利用(13)式和(4),对n=0,……,N -1,有

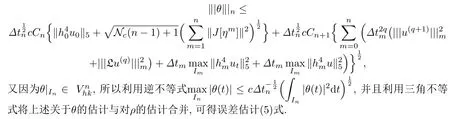
设ℓm(s)表示单元E=(-1,1)上的m次Legendre多项式.进一步,在E上定义多项式

则当m ≥0时φm+1(s)在E内有m+1个实根,sα,α=0,1,……,m.特别地sm=1是根.

设是L2([a,b])投影算子,即对任意的u ∈L2([a,b])有

则当u ∈H4([a,b])([a,b])时,满足如下估计式[11-12]:

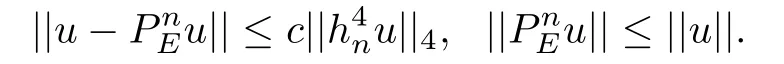
定理2设u是问题(1)的解,U是格式(3)的解,并且初始值U0=u0,则存在不依赖Δt和h的正常数c使得对0≤n ≤N,

由Legendre正交展开知

进一步,构造q-1次多项式W(x,s)使得W(x,1)=ω(x,1),且其余项为

其中是待定系数,而bj是(5) 中的已给系数.显然R(1)=0.令ρ=u-W,用分部积分,余项R和投影的定义,有

现在要求满足q-1阶线性方程组

它的系数矩阵有如下结构

现令θ=W -U,又由于问题(1) 的解u满足(14),有

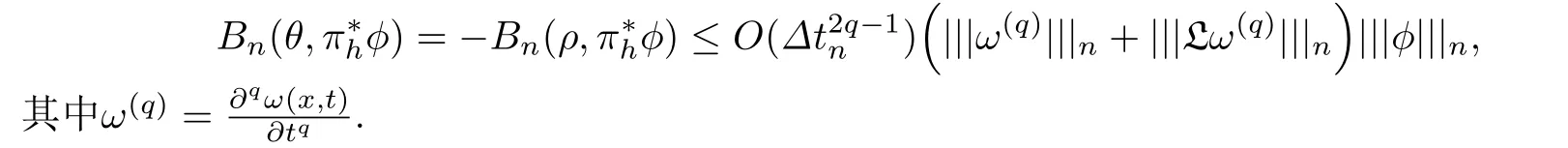
首先,取φ=θ,积分并用Young不等式和引理2后有

假设h=O(Δt),则对所有时间单元求和并用有限元空间的逆性质和Gronwall引理,得

其次,取φ=(t-tn)θt,则φn+=0并有限元空间的逆性质和引理2有

利用局部逆性质,上式变为

于是结合(18)式,(19)式和(20)式,得

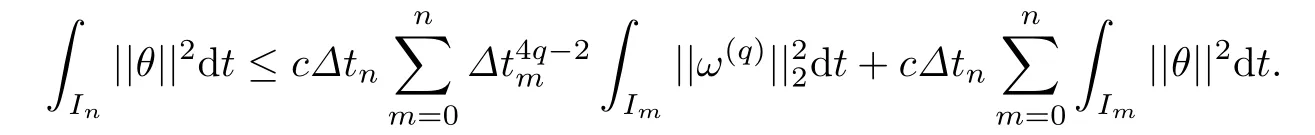
上式利用Gronwall 不等式,再求和后代入(18)式有

最后利用L2(Ω)投影的性质和余项R的定义,可得对0≤n ≤N,

§4 数值算例

为验证本文所提格式的可行性以及理论分析结果的合理性,考虑一维对流扩散方程[13]

其精确解u(x,t)=exp(5x-(0.25+0.01π2)t)sin(πx).在数值计算过程中,试探函数空间取时间线性,空间三次Lagrange插值为基函数,检验函数空间取时间线性,空间分片常数为基函数.

表1.1分别给出固定时间步长Δt=0.001,而空间步长分别取h=1/2,1/4,1/8,1/16时,时空误差||u-U||L∞(L2)和时间节点误差‖uN -UN‖L2的计算值和收敛阶.从表中数据可以看出,当步长h折半递减时,两种误差数据的收敛阶接近四阶,吻合理论分析结果.

表1.1 当固定时间剖分Δt=0.001时,空间方向的误差及收敛阶

表1.2中分别给出固定空间步长h=0.001时,而时间步长分别取k=1/5,1/10,1/20,1/40时,时空误差||u-U||L∞(L2)和时间节点误差‖uN -UN‖L2的计算值和收敛阶.从表中数据可以看出,当步长Δt折半递减时,时空误差数据的收敛阶接近二阶最优收敛,而时间节点处误差数据的收敛阶接近三阶,呈现超收敛性,符合理论分析结果.

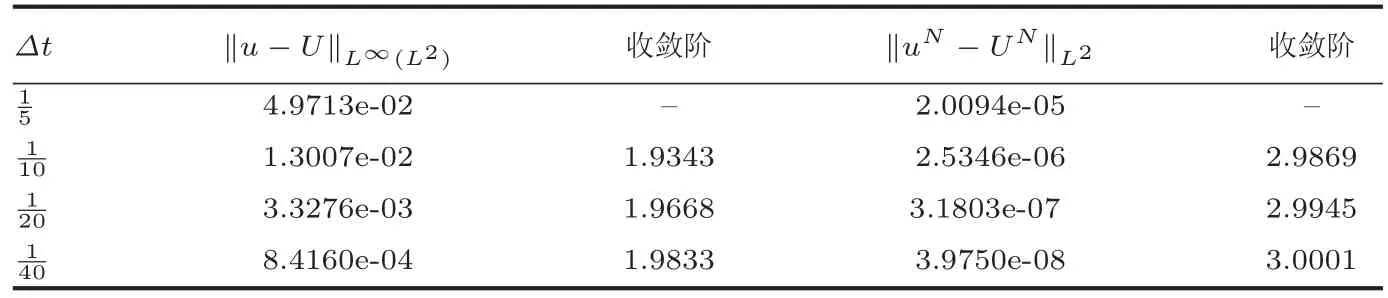
表1.2 当固定空间剖分h=0.001时,时间方向的误差及收敛阶

表1.3分别给出了固定时间步长Δt=0.002,而空间步长分别取h=1/20,1/40,1/80,1/160时,t=tN时刻对偶剖分节点处空间导数模误差和原始剖分节点处空间导数Eorigi-nodes:=模误差.从实验数据发现原始剖分节点处导数项的收敛阶为三阶,而对偶剖分节点,即最佳应力节点处收敛阶为四阶,具有超收敛性.这些实验数据说明时间间断时空体积元格式能够有效求解对流扩散问题,且实验数据与理论分析结果吻合.

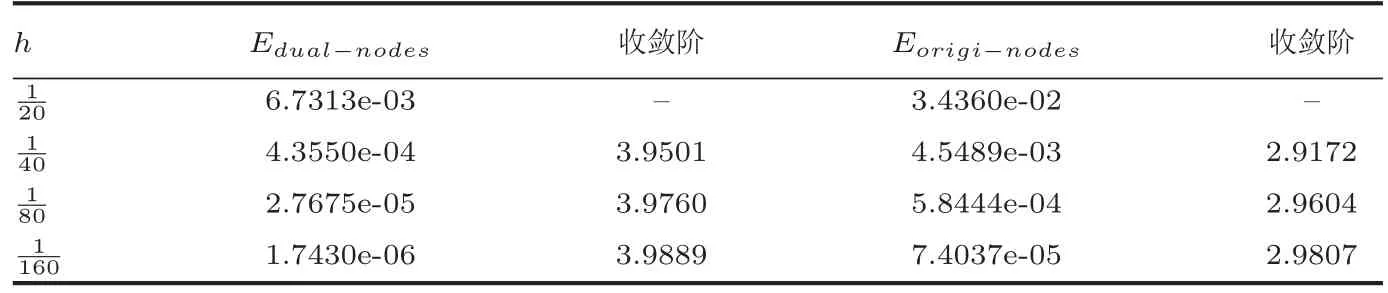
表1.3 当固定时间剖分Δt=0.002时,导数在空间方向的误差及收敛阶

§5 结论

本文针对一维对流扩散问题提出了时间间断时空有限体积元格式,利用有限差分和有限体积元法相结合的技巧证明了格式的L∞(L2)-模最优收敛误差估计,用单元正交分解法证明了格式在时间节点处的超收敛估计.最后为了说明文中所提格式的可行性,给出了数值算例.从理论分析和数值实验数据可知,本文所提出的时间间断时空有限体积元方法在时间剖分节点处具有超收敛性,高于文献[8]中有限体积元法的收敛阶.本文所提出的时空方法有别于此前的时间间断时空有限元法(参见文献[1-7]),文献[1-6]所涉及方法是时间间断而空间连续的时空格式,文献[7]的方法是时间间断有限元,空间一次有限体积元的时空格式,而本文所提出的方法时间间断有限元,空间三次有限体积元的时空格式,具有计算精度高且能保持物理量的局部守恒性等优点,并通过数值实验发现在最佳应力点处导数的最大绝对误差收敛阶高于其他节点处的收敛阶.为此,后续工作中将分析导数超收敛估计.