陶 亮，刘海鹏，王 蒙

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

0 引言

传统的信号采样受限于奈奎斯特定理[1-2]，采样速率低下，急需一种新的信号采样方法，在这种情况下压缩感知[3]被提了出来。

压缩感知中最重要的环节就是信号重构，它的作用就是在观测值较少的情况下精确、快速地恢复原信号。目前最直接的重构方法就是在L0范数下求解最优化表达式[4-5]。于是，为了提高信号的重构速率，MOHIMSNI G H等人在2009年提出了基于平滑L0范数的重建。随后在此算法上，研究者们相继提出了基于SL0的TSL0(Thresholded SL0)[6]算法、基于SL0的NSL0(Newton SL0)算法[7]和L0AM(L0 Norm Approximation)算法[8]。在以上所提算法中，NSL0算法重构得到的图像是最优的[9]，但NSL0算法重构质量依然不足。于是本文在NSL0算法的基础上提出了ACNSL0算法，该算法采用反余弦函数来近似估计L0范数，结合修正牛顿法[10-12]和阻尼牛顿法，获得的一种更快速、高效的信号重建算法，经过仿真，得出该算法在重构误差和峰值信噪比[13-14]方面有较大改善。

1 NSL0算法

NSL0算法的主要思想是采用双曲正切函数族来取代SL0所采用的高斯函数族，用修正牛顿法取代最速下降法，而且相对于高斯函数，双曲正切函数更陡峭，所以会更加逼近L0范数，重构的效果理论上更好。双曲正切函数的数学表达式如下：

式中，si为稀疏系数s的分量，σ 为趋近于0的递减参数。在NSL0算法中，σ 的取值尤其关键，由图1可以看出，当σ 较大时，函数值Fσ(si)变得非常平滑，局部最大值也变得极少，可以避免受到局部极值点的影响；当σ非常小时，Fσ与L0范数非常接近，但是函数曲线很不平滑。基于这种性质，所以一开始直接选取σ 的最大值(即4max|si|)，然后以一定间隔递减，最后逐渐逼近全局最优解。因为NSL0算法精度高，所以得到了广泛的应用。但是NSL0算法采用双曲正切函数来逼近L0范数未必是最优的，也就是它的重构质量依然不够好，故本文提出来一种改进的ACNSL0算法。

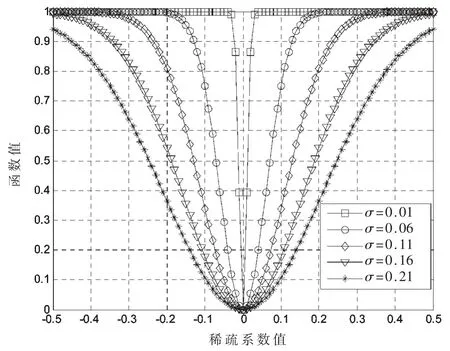
图1 双曲正切函数在不同σ 下的函数逼近效果

2 ACNSL0算法

ACNSL0算法主要原理是采用反余弦函数替代双曲正切函数去逼近L0范数，如图2所示，由于反余弦函数比SL0采用的高斯函数、NSL0采用的双曲正切函数更具有“陡峭性”，因此其在数学意义上也更逼近于L0范数，因而理论上重构效果也更好，并加入牛顿阻尼，以此选择合适的步长，不断更新，直到重构出信号。

本文提出的反余弦函数的数学表达式如下：

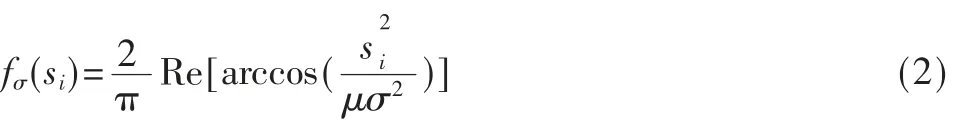
其中，Re表示函数值fσ(si)取实部，μ 可以取一个大于1的常数。由此可得到：

定义反正弦函数族如下：

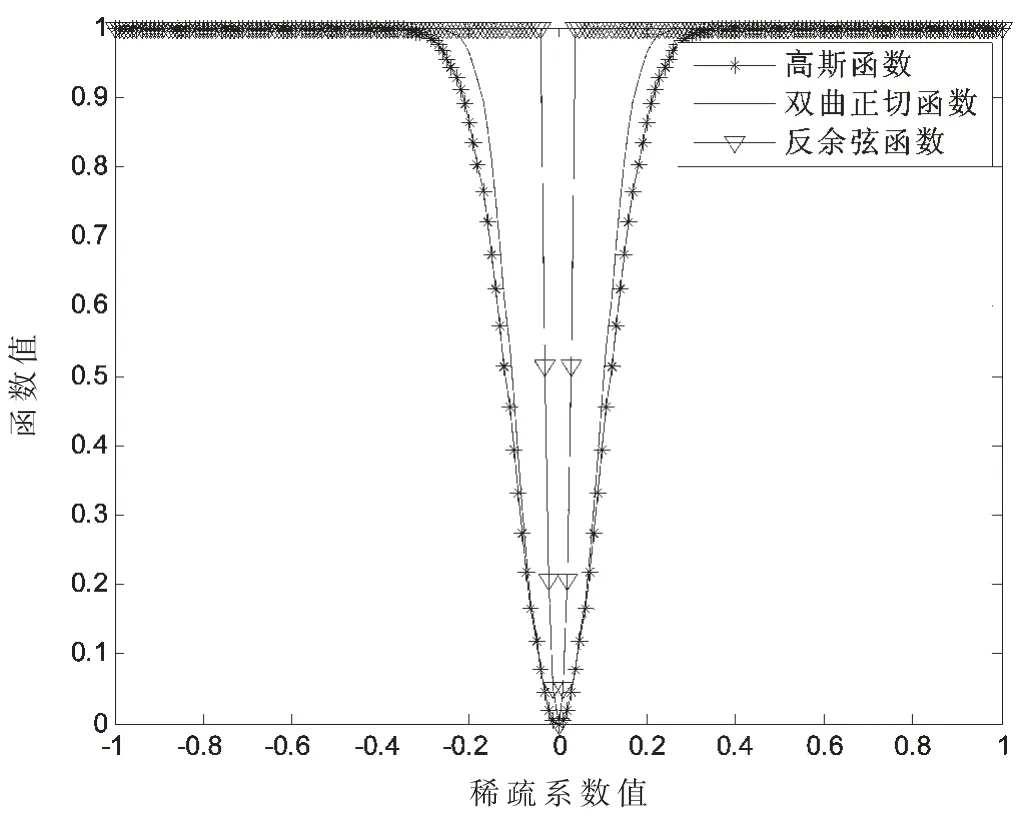
图2 当σ=0.1时3种函数逼近效果对比图

其中，N表示信号的长度，当递减参数σ 非常小时，函数Fσ(s)的函数值等同于稀疏系数s中不为0元素的个数，所以公式min||s||0s.t.y=As可以转换为：

其中，||s||0表示稀疏系数中非0系数的个数。该算法同NSL0算法一致，采用修正牛顿法，从而避免出现“锯齿”现象，修正牛顿公式计算如下：

接着求二阶偏导：

由于海森矩阵的特征值不一定是正定的，现提出式(8)表示的构造矩阵对其进行修正，求得：

得到修正法牛顿方向：

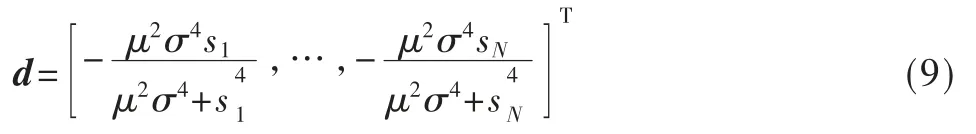
但是上面提到的修正牛顿法存在一个缺点，就是迭代公式为定长迭代，对于目标函数，有时候会出现迭代发散的情况，这表明牛顿法不能保证函数值稳定地下降，对此，为了消除该弊病，引用了牛顿阻尼法。牛顿阻尼法的最优步长因子满足：

其中，sk表示k次迭代后的重构系数，dk表示k次迭代后的步长，由式(10)可得到本算法的最优步长因子为γk=-sk/dk。

本文提出的算法(ACNSL0算法)如下：

输入：传感矩阵AM×N，观测矩阵YM×N；

(1)初始s=AT(AAT)-1Y；σj=βσj-1，σ 为递减数列，β 为衰减因子。

(2)外部循环：j=1，2，3，…，J。

①令σ=σj；

③内部循环：l=1，2，3，…，L。

(a)计算修正后的牛顿方向：

(b)用牛顿阻尼法选择最优步长γ，对重构信号进行更新s=s+γd；

(c)根据梯度投影原理，得到s←s-AT(AAT)-1(As-y)；

④σj=βσj-1，更新σ，其中β 为衰减因子

3 仿真结果与分析

3.1 一维信号测试

为了测试ACNSL0算法对信号的重构效果，首先用一维信号进行仿真测试，信号的长度为N=128，仿真结果如图3所示，带空心圆球的黑线表示重构信号，黑线表示重构信号。由图3可以看出，两种类型的黑线基本重合，且重构误差为2.208 4×10-13，因此可得出本算法可以达到对一维信号的高精度重构。

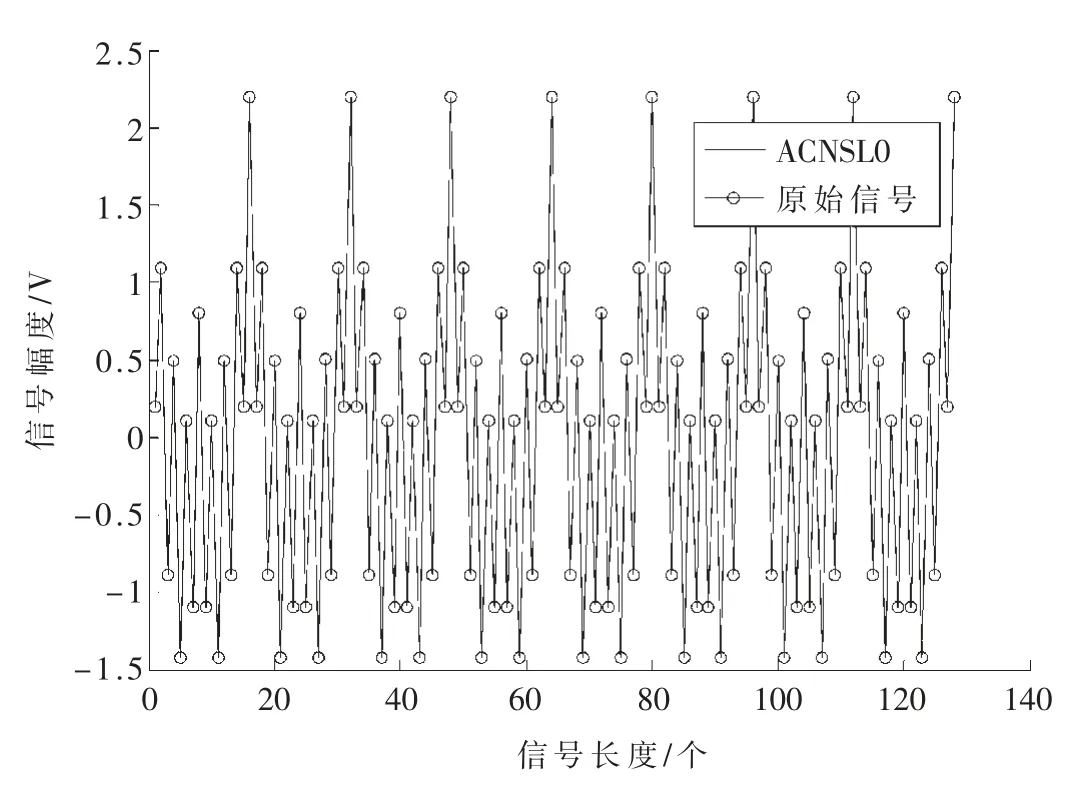
图3 ACNSL0算法的一维信号测试

然后给出3种算法的峰值信噪比(PSNR)对比图，如图4所示，随着压缩比的增大，3种算法的峰值信噪比也相对增大，但是ACNSL0算法压缩比在[0.1，0.9]区间中始终大于另外两种算法，可见其重构性能的优越性。

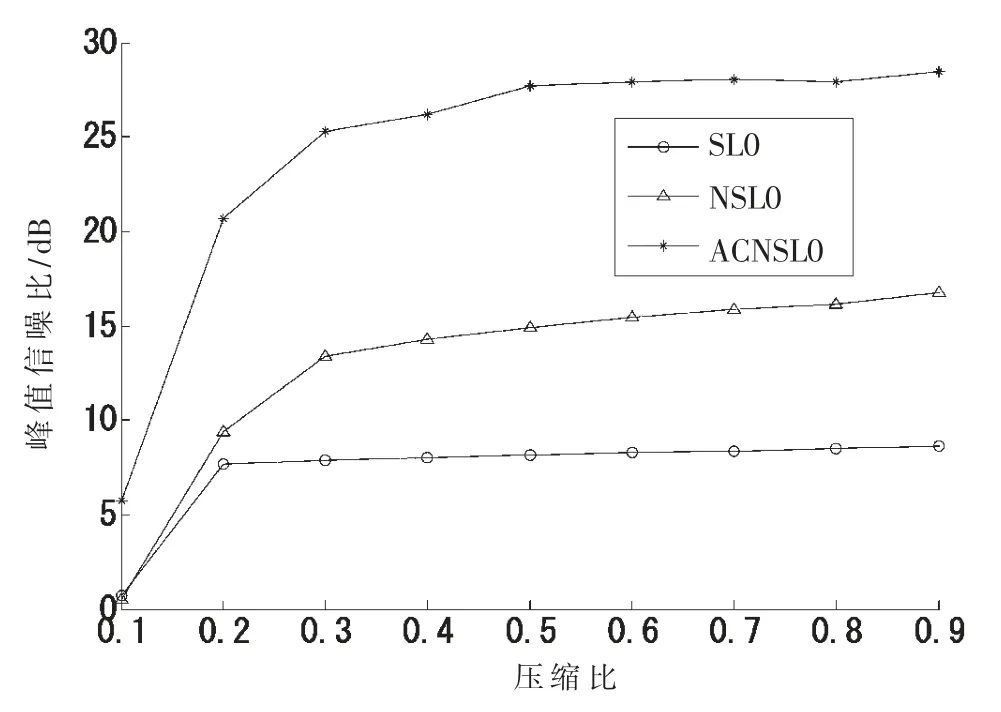
图4 3种算法的SRNR对比图

3.2 二维图像重构测试

为了更深一步验证该算法的性能，最后验证其对二维图片的重构效果。仿真结果如图5～图7所示。

图5 3种算法在压缩比为0.4时的二维重构实验

图5～图7分别是SL0、NSL0、ACNSL0算法在压缩比分别为0.4、0.5和0.6时的重构图像，随着压缩比的增大，3种算法的峰值信噪比(SRNR)均明显上升。但从表1～表3均可以可以看出，虽然本算法重构时间多于另外两种算法，但无论压缩比为0.4、0.5还是0.6时，ACNSL0算法的峰值信噪比始终最大，重构误差也是最小的。由此可以看出该算法的优越性。

4 结论

针对压缩感知中NSL0算法信号重构精度的不足，本文在此算法的基础上提出了一种改进算法，命名为ACNSL0算法，该算法用反余弦函数代替NSL0所采用双曲正切函数去逼近L0范数，并引入牛顿阻尼法使本算法稳定收敛，经过一维和二维仿真对比，发现该算法的重构质量明显优于另外两种算法。但在运行时间上，由于ACNSL0算法的复杂性，故稍慢于另两种算法，后续将针对算法运行时间方面做进一步研究。

图6 3种算法在压缩比为0.5时的二维重构实验

图7 3种算法在压缩比为0.6时的二维重构实验

表1 SL0、NSLO、ACNSL0算法压缩比为0.4时二维重构性能比较

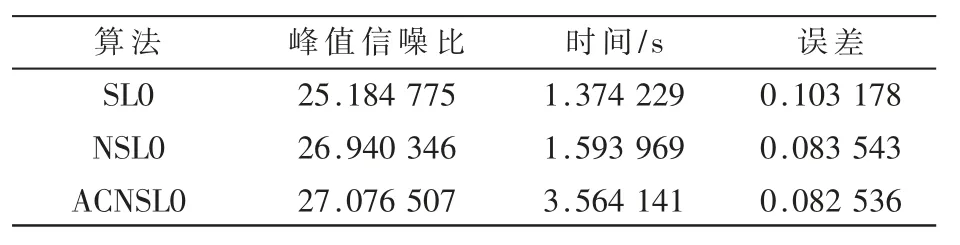
表2 SL0、NSL0、ACNSL0算法压缩比为0.5时二维重构性能比较

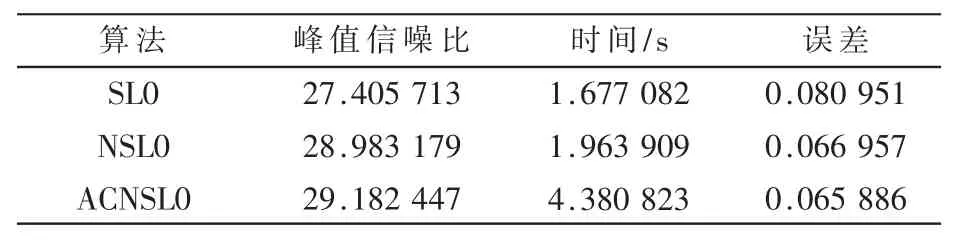
表3 SL0、NSL0、ACNSL0算法压缩比为0.6时二维重构性能比较