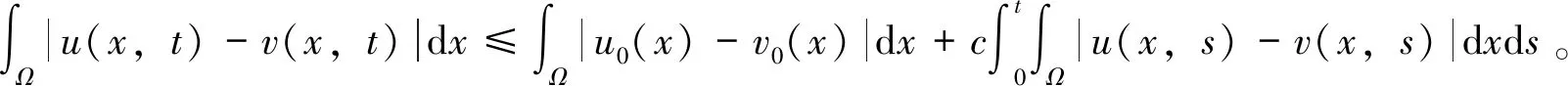曾羽群

(集美大学理学院，福建 厦门 361021)

0 引言

21世纪以来，发展的p(x)-Laplace方程

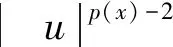
(1)

引起许多偏微分方程研究者的兴趣。从形式上看，方程(1)不仅是传统的发展p-Laplace方程的推广，该方程还有着自身的物理应用背景，比如它来自于21世纪新兴的电磁变流体理论[1-2]、非标准的图像处理[3-4]等。其中：Ω⊂RN是具有光滑边界∂Ω的有界区域；p(x)是一个可测函数。如果a(x,t)=1,方程(1)的初边值问题解的存在唯一性问题、正则性问题、大时间渐近行为和爆破问题等已经被广泛研究[5-7]。如果a(x,t)=d(x)α,其中d=dist(x,∂Ω)是距离函数，文献[8-11]研究了方程

(2)

解的存在唯一性，文献[12]研究了解的内部正则性。如果f(x,u,t)=0,并假设a(x,t)=a(x)满足

(3)

文献[13-14]研究了解的存在性和稳定性。实际上，如果a(x,t)|x∈∂Ω=0,并假设方程(1)有解u∈L1(0,T;Wp(x)(Ω)),那么对于方程(1)的两个解u(x,t)、v(x,t),只要

|f(u,x,t)-f(v,x,t)|≤c|u-v|。

(4)

由于a(x,t)在边界∂Ω的退化性，可以不用Dirichlet边界条件

u(x,t)=v(x,t)=0,(x,t)∈∂Ω×(0,T),

(5)

就可以证明

(6)

本文将借鉴文献[13-15]的方法，研究方程(1)具有如下初边值条件

u|t=0=u0(x),x∈Ω,

(7)

u(x,t)=0,(x,t)∈Σ1,

(8)

解的存在唯一性。与文献[13-15]的主要不同在于，本文需要部分边界条件(8),其中Σ1⊆∂Ω×(0,T)仅仅是一个子流形。

1 基本函数空间及其弱解的定义

。

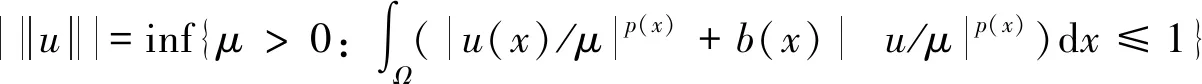
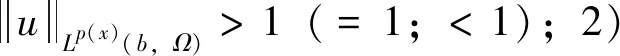
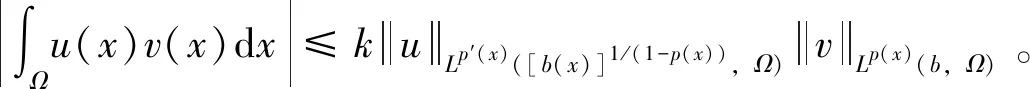
ps(x)=p(x)s(x)/(1+s(x)),

定义1 若函数u(x,t)满足

u∈L∞(QT),ut∈L2(QT),u∈L∞(0,T;W1,p(x)(a,Ω))，

(9)

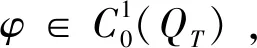
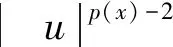
(10)

则称函数u(x,t)为方程(1)的弱解。其中初值条件(7)在如下意义下成立

(11)

部分边界条件(8)是在迹的意义下成立。

文中，假设a(x,t)≥0且对于任意固定的t∈[0,T),

a(x,t)> 0,x∈Ω。

(12)

定理1 设对于任意固定的t∈[0,T)、a(x,t)满足式(12)、at(x,t)≤0及条件(w1)(w2),

(13)

f(u,x,t)是连续函数且满足式(4),那么方程(1)有一解u(x,t)满足初值条件(7)。并且当

(14)

u(x,t)在迹的意义下满足部分边界条件(8)。

定理2 设a(x,t)满足式(12)及条件(w1)(w2),同时对于充分大的n,

(15)

其中，对任意t∈[0,T)，Ωt/n={x∈Ω:a(x,t)>1/n}，若u(x,t)、v(x,t)是方程(1)的弱解，具有不同的初值u0(x)、v0(x),并具有相同的部分边界条件

u(x,t)=v(x,t)=0,(x,t)∈Σ1,

(16)

则有

在茅台成立之初，由于茅台酒酿造工艺非常独特，对酿造环境的要求非常苛刻，茅台酒不能实现大规模快速生产。这样的处境，成为了当时横亘在急需扩大生产的茅台面前一道难以逾越的鸿沟。“一定要创新技术”这条坚定的信念在所有茅台人心中留下了烙印，茅台也自那时起开始了真正意义上的规模建设。经由茅台人的不懈努力，茅台酒的产量从1978年的1068吨发展到2003年的1万吨，实现了茅台酒年产万吨的梦想。茅台酒万吨梦圆，完成了老一辈革命家的夙愿，这是茅台发展的历史丰碑，也为茅台进一步的发展奠定了基础。除此之外，在“十二五”期间，茅台还进行了一次全方位的厂地扩建，使得茅台酒厂成为世界上生产规模最大的酿酒企业。

(17)

其中Σ1={(x,t)∈∂Ω×(0,T):a(x,t)>0}。

稳定性(17)隐含解的唯一性成立，只不过需要条件(15)，如果没有这一条件，那么解的唯一性还需要将来另外论证。

2 定理1和定理2的证明

2.1 定理1的证明

本节用抛物正则化证明定理1。

考虑正则化问题

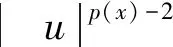
(18)

具初边值条件

u(x,0)=u0ε(x),x∈Ω,

(19)

u(x,t)=0,(x,t)∈∂Ω×(0,T)。

(20)

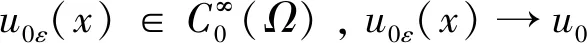
(21)

在方程(18)的两边同乘以uε，有

(22)

(23)

特别地，

(24)

同时，在方程(18)的两边同乘以uεt，对任意的t∈[0,T),在Qt=Ω×(0,t)上积分，有

(25)

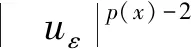
(26)

由式(21)，应用Young不等式，有

(27)

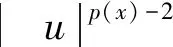
(28)

特别地，当a(x,t)=a(x),式(28)的证明可见文献[22]。尽管本文考虑的是a(x,t)的情况，但完全可以类似证明，故在此不再重复其证明。

2.2 定理2的证明

设u(x,t)、v(x,t)为方程(1)的弱解，具有不同的初值条件u(x,0)、v(x,0)，具有相同的部分边界条件(16),其中，Σ1={(x,t)∈∂Ω×(0,T):a(x,t)>0}。

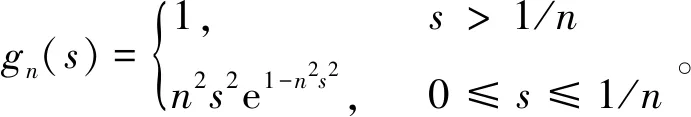
任意固定的t∈[0,T),定义

由于u(x,t)、v(x,t)∈L∞(0,T;W1,p(x)(a,Ω))，故gn(u-v)∈L∞(0,T;W1,p(x)(a,Ω))。因为u(x,t)、v(x,t)具有相同的部分边界条件(16)，在边界∂Ω上，当a(x,t)> 0时，u(x,t)=v(x,t)=0，通过一个极限过程,可以选取φntgn(u-v)作为检验函数，于是，

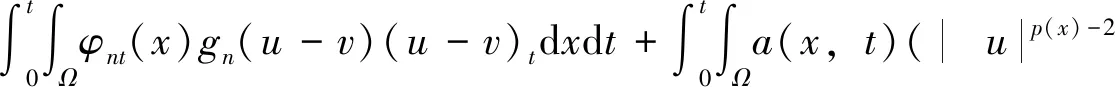
(29)

(30)

(31)

同时又有：

(32)

(33)