邓严林 侯兰宝 严 政

(1.荆楚理工学院 数理学院,湖北 荆门 448000;2.长江大学 信息与数学学院,湖北 荆州 434023)

特征值问题的研究一直是现代微分几何的热点问题,具有深刻的物理背景和重要的理论价值.而关于紧黎曼流形上自伴椭圆算子的特征值研究则备受关注,这是因为紧黎曼流形上椭圆算子具有离散特征值,而如何对这些特征值做出估计则是一个重要的研究课题,相关研究成果可参看文献[1-3].

近年来,关于光滑度量测度空间上自伴算子的特征值问题也受到很多人的关注和研究[4-6].所谓的光滑度量测度空间是指一个黎曼流形M匹配上一个光滑测度e-fdv,这里的f是M上的一个实值光滑函数,dv是与黎曼度量〈,〉相关的黎曼体积元,因而,通常用(M,g,e-fdv)来表示光滑度量测度空间.在(M,〈,〉,e-fdv)上,可以定义漂移拉普拉斯算子:

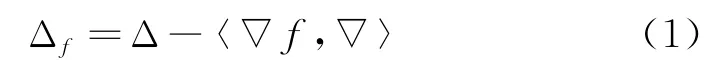
式中:Δ和∇分别表示M上的拉普拉斯算子和梯度算子.在光滑度量测度空间上,还可以定义权重Ricci曲率(也称为Bakry-Emery Ricci曲率)

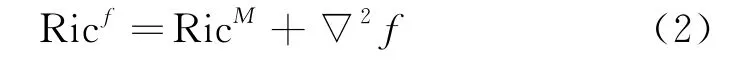
式中:RicM是M的Ricci曲率;∇2表示Hessian算子.当κ是常数时,方程Ricf=κ〈,〉就是梯度Ricci孤立子方程,在Ricci流的研究中起着重要作用.

关于Ricci孤立子的特征值问题的研究成果,参看文献[3],还可以定义m阶权重Ricci曲率(也称为m-Bakry-Emery Ricci曲率)

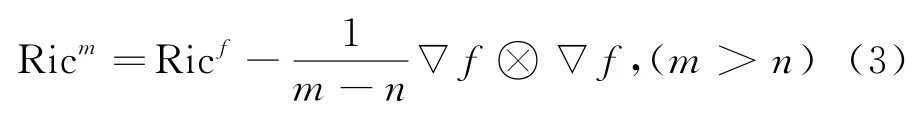
当m=n时,令f为常数且Ricm=RicM.当m→∞时,Ricm=Ricf,因而权重Ricci曲率也称为∞阶的.关于光滑度量测度空间的更多细节,参看文献[7].

本文中,将研究双漂移拉普拉斯算子的特征值问题.设(M,〈,〉,e-fdv)是具有光滑边界∂M的n维紧致连通光滑度量测度空间,考虑下述方程:

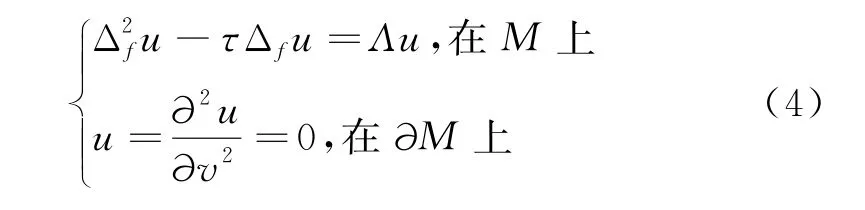
式中:v是边界∂M的单位外法向量;τ是非负常数.当f是常函数时,方程(4)是经典的双调和算子的特征值问题,用来刻画物理中的圆盘张力问题,而常数τ与圆盘的横向张力有关,因而也称为圆盘振动问题[1].因而方程(4)称为双漂移拉普拉斯的特征值问题,也称为带权圆盘振动问题[8].由自伴算子谱理论可知,方程(4)具有离散谱,即其特征值可以排成下述单调数列:

式中:Λi可以重复出现其重数(即特征空间维数)次.关于方程(4)的第一非零特征值估计,可以得到下述结论.

定理1设(M,〈,〉,e-fdv)是具有光滑边界∂M的n维紧致连通光滑度量测度空间,且Λ1是方程(4)的第一非零特征值.当m阶权重Ricci曲率有下界(m-1)ξ＞0时,可得

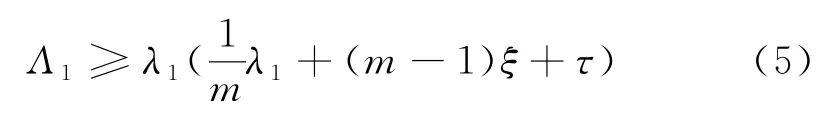
式中:ξ为正常数;τ为非负常数;λ1为漂移拉普拉斯算子的第一Dirichlet特征值.当且仅当M等度于一个曲率为ξ的欧氏半球且f是常函数时,不等式中等号成立.

本文第二部分将考虑双漂移拉普拉斯算子在Dirichlet边界条件下的特征值问题,得到下述结论.

定理2设(M,〈,〉,e-fdv)是具有光滑边界∂M的n维紧致连通光滑度量测度空间,且Λ1是问题

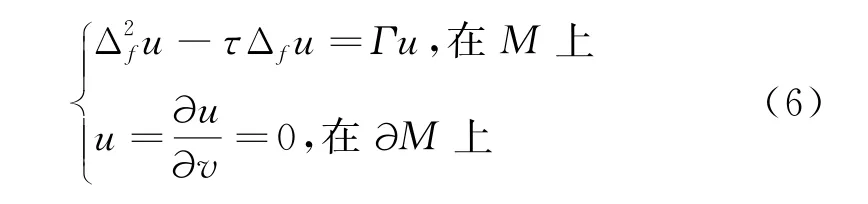
的第一非零特征值.当m阶权重Ricci曲率有下界(m-1)时,可得

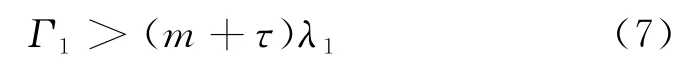
式中:τ为非负常数;λ1为漂移拉普拉斯算子的第一Dirichlet特征值.

当τ=0时,定理1即为文献[9]中的定理1.1;定理2即为文献[10]中定理1.5.

1 预备知识

本节将介绍一些概念和结论,他们将在主要定理的证明中起到关键作用.设(M,〈,〉,e-fdv)是具有光滑边界∂M的n维紧致连通光滑度量测度空间,S(X)=∇Xv是边界∂M的形状算子,则第二基本形式Ⅱ(X,Y)=〈S(X),Y〉.这里X,Y∈T∂M,∇是M的黎曼联络.则S的特征值称为边界∂M的主曲率,而∂M的平均曲率这里trS表示S的迹,而权重平均曲率

下面给出漂移拉普拉斯算子的Reilly公式[11],设g是M上的光滑函数,而dμ=e-fdv,则下述恒等式成立

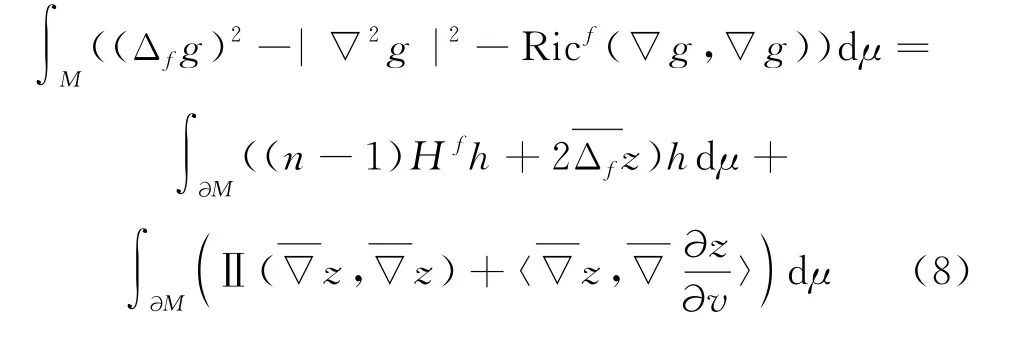
引理1设(M,〈,〉,e-fdv)是具有光滑边界∂M的n维紧致连通光滑度量测度空间,设g是M上的光滑函数,而可得

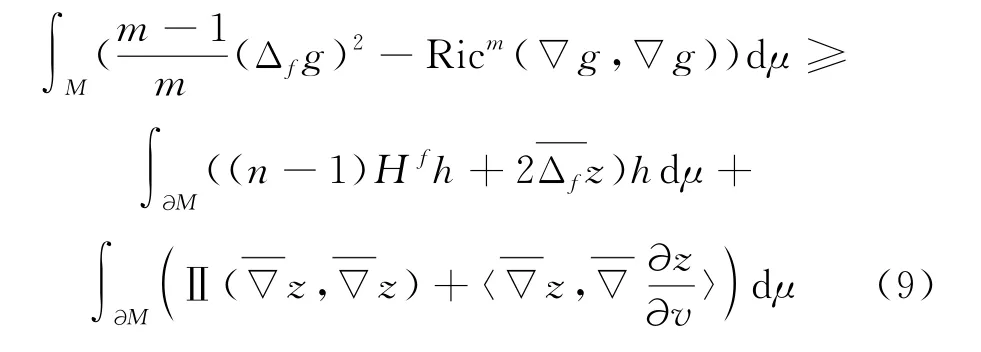
当m=n时,则f是常数,当且仅当〈,〉时等式成立;当m＞n时,当且仅当和

2 主要结论的证明

2.1 定理1的证明

设u是方程(4)的第一非零特征值Λ1对应的特征函数,有

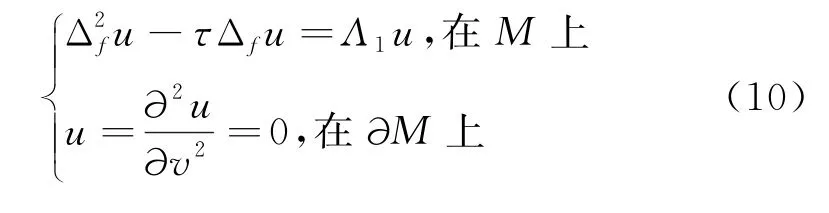
则由散度定理可得:

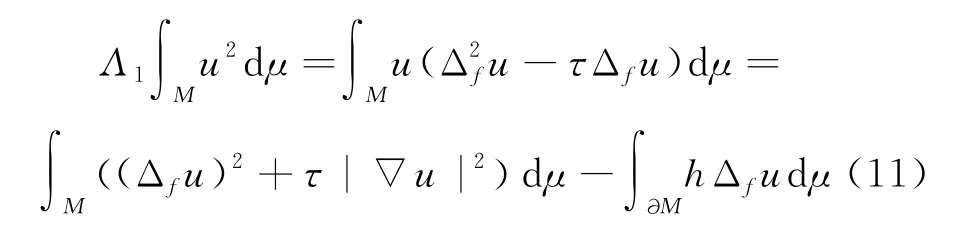
在边界∂M上,可以得到

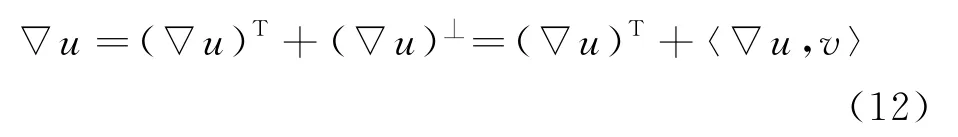
式中:(∇u)T是切于∂M的部分;(∇u)⊥是垂直于∂M的部分.而由,可得

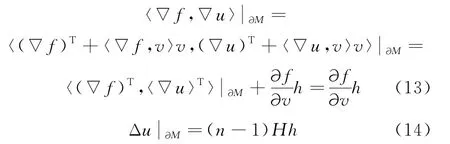
则由式(13)、(14)可得

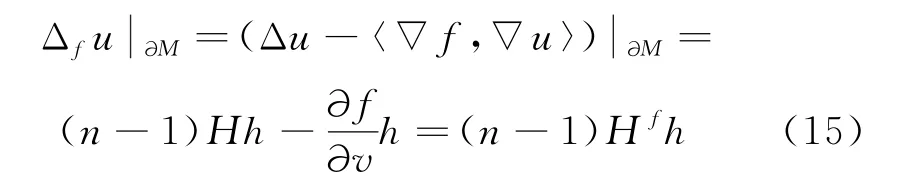
将公式(15)代入公式(11)可得

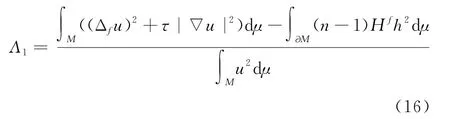
将u代入式(9),注意到,可得

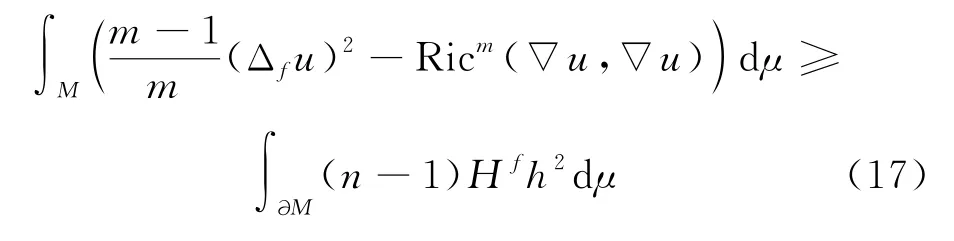
注意到m阶权重Ricci曲率有下界(m-1)ξ＞0,可得

将式(18)代入式(16),可得

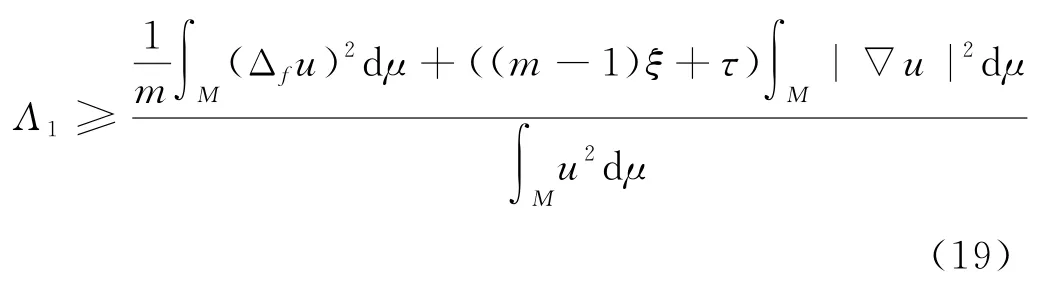
再由Poincare不等式和Schwarz不等式可得

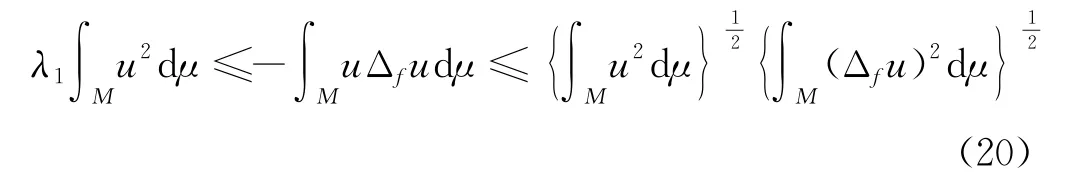
由式(20)可得

当且仅当u是漂移拉普拉斯算子的第一Dirichlet特征函数时,式(21)等号成立.将式(21)代入式(19),并使用Poincare不等式,可得

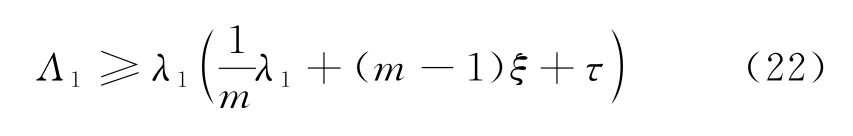
接下来,讨论式(22)中等式成立的情形.如果Λ1=,则式(21)等号成立,所以在M上,Δfu=-λ1u,则可得τΔfu=Λ1u,可得再注意到Λ1=

当m=n时,f为常函数,则漂移拉普拉斯算子Δf退化了拉普拉斯算子Δ,则λ1=mξ＞0即为拉普拉斯算子Δ的第一特征值,则由文中定理可知,当且仅当M等度于一个曲率为ξ欧氏半球时,式(22)中等号成立.

当m＞n时,式(22)中等号成立,意味着式(9)和式(21)中等号成立.当式(9)中等号成立时,由引理1可得

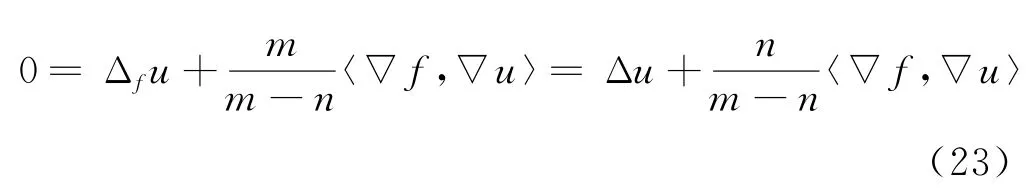
在式(23)两边乘以函数u并在M关于权重测度积分可得

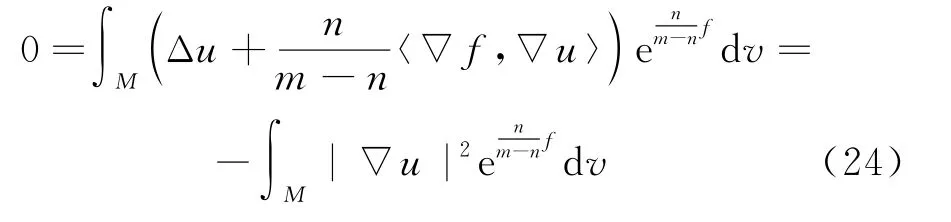
由上式可知u是一个常函数.而当式(21)中等号成立时,可知u是漂移拉普拉斯算子的第一Dirichlet特征函数,则与u是一个常函数矛盾,因而,当m＞n时,式(22)中等号不能成立.

综合以上分析可得:当且仅当等度于一个曲率为ξ欧氏半球且f是常数时,不等式(m-1)ξ+τ)中等号成立.定理1证毕.

2.2 定理2的证明

设w是问题(6)的第一非零特征值Γ1对应的特征函数,因而有

则

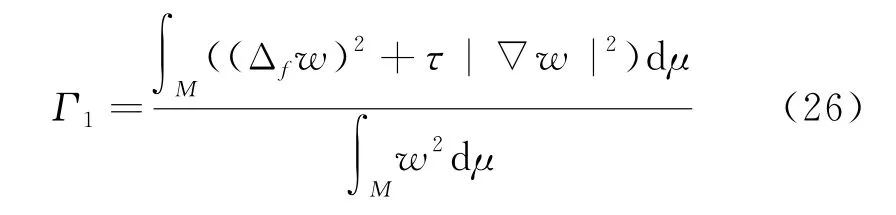
将w代入式(9)中,注意到

将式(27)代入式(26),可得

当m=n时,f为常函数,则漂移拉普拉斯算子Δf退化了拉普拉斯算子Δ,则由文献[10]中定理1.5可知,Γ1＞(m+τ)λ1.

当m＞n时,由与定理1类似的讨论,可得Γ1＞(m+τ)λ1.定理2证毕.