球对称瞬态非傅里叶热传导分析1)

2021-04-25刘承斌龚顺风王惠明

力学与实践 2021年2期

刘承斌龚顺风王惠明

∗(浙江大学土木工程学院，杭州310058)

†(浙江大学工程力学系，杭州310027)

球壳结构因其受力合理在工程中有广泛的应用，大至储油罐，小至压电传感器等。当球壳结构工作于温差突然有较大变化的环境中时，急剧的温度变化使得结构内部产生瞬态热应力。通常将这种短促时间内出现的热应力数值上非常大的现象称为热冲击，热冲击有可能产生很大的拉压应力，甚至可能达到脆性材料的破坏应力，从而造成材料破坏。以往常规热分析大多基于经典傅里叶热传导定律，这种经典傅里叶热传导的描述可以满足绝大部分工程理论分析的精度要求，但存在热传播速度无穷大这一与实际物理规律不符合的弊端。随着研究的不断深入和应用范围的不断扩大，特别是在极端环境下服役时，经典理论已不能满足分析要求[1]。为克服经典傅里叶热传导定律的局限性，Cattaneo[2]和 Vernotte[3]给出了能够描述热以有限速度传播的双曲型热传导方程，被称为C-V 方程或非傅里叶热传导方程。这种广义热传导问题可采用积分变换、差分法、有限元以及解析法等多种方法进行求解。积分变换方法将时间域的偏微分方程变换为频域的常微分方程，再进行求解，然后进行积分反变换，求得时域响应。Jiang等[4]利用拉普拉斯变换，针对某些边界条件，得到了空心球壳受热冲击的解析解。Babaei 等[5]利用拉普拉斯变换和常规数值反变换得到功能梯度空心球壳的广义热传导响应。Conker 等[6]将拉普拉斯变换和修正的数值反变换方法相结合，探讨了材料特性按指数变化的功能梯度厚壁圆柱壳和球壳双曲型非傅里叶热传导问题。Wang 等[7]利用积分变换研究了考虑界面裂纹的层状复合材料的非傅里叶热传导现象。有限差分方法根据不同的边界条件和初始条件选择合适的差分格式，将问题离散化后求解，所采用的差分格式决定了求解精度，且必须满足收敛性和稳定性要求[8]。广义热弹性有限元方法，可避免数值积分反变换造成的截断误差，直接在时间域求解，但推导相对复杂[9-11]。分离变量法[12-15]在球壳表面受热冲击作用的热传导分析中也非常有效。此外，Rahideh等[16]利用微分求积法研究了叠层功能梯度平面域非傅里叶热传导问题。张浙等[17]对非傅里叶热传导的研究进展做了评述，从实质、模型的建立和求解及应用于实验等多个方面进行了论述，并指出了今后的研究方向。蒋方明等[18]进一步介绍了非傅里叶导热的研究进展。近年来，Moosaie[19]研究了空心球的球对称瞬态热传导问题，为便于求解，将解分为两部分之和：一部分稳态解对应非齐次边界条件，另一部分瞬态解对应齐次边界条件。Zhao 等[20]通过分离变量法结合杜哈梅原理，分析了实心球外受任意表面热冲击条件下的非傅里叶导热响应。许光映等[21]利用积分变换方法探讨了非傅里叶导热边界条件对激光辐射生物组织热传导的影响。刘承斌等[22]从三维压电弹性理论出发，利用拉普拉斯变换结合状态空间法，分析了压电球壳受表面球对称热冲击作用下的热弹性问题。张彦博等[23]基于双曲型单相延迟非傅里叶热传导方程，采用有限元法研究了含裂纹厚壁圆筒结构在热冲击载荷下的热力学数值解。陈豪龙等[24]提出微分转换双重互易边界元法求解功能梯度材料非傅里叶瞬态热传导问题。结果表明时间步长对计算结果的影响较小，该方法可以有效求解功能梯度材料非傅里叶瞬态热传导问题。郭松林[25]基于双相延迟非傅里叶热传导模型对工程中常见的圆柱、板、涂层以及夹芯板等结构在热冲击载荷作用下的裂纹问题进行了分析，系统分析了结构热弹性响应和裂纹尖端应力强度因子。

综上所述，尽管广义热传导问题已有很多有效的求解方法，但随着新材料技术的不断发展和服役环境的更加严苛，需要寻求计算效率高且准确的方法。本文针对球对称瞬态非傅里叶热传导问题，给出了两种不同的求解方法，并通过具体算例分析比较了两种方法的计算效果。

1 球壳瞬态热传导基本方程

考虑内外半径分别为a和b的空心球壳受球对称热冲击作用 (图 1)，球对称情形的 L–S 型广义热传导方程为

式中，k33为径向热传导系数，τ为热松弛时间，T为温度变化值，ρ为质量密度，cv为比热容。由非傅里叶定理可知

式中,∇2=r∂/∂r,Θr=rqr，qr为径向热流密度,符号上面的·表示对时间t求导。

图1 球坐标及球壳示意图

存在三种不同的温度边界条件：给定边界处的温度、热流密度或者两者的线性组合。为便于推导，本文考虑温度边界条件，其他边界条件采用同样的步骤可以类推。球壳内外表面的温度边界条件和初始条件可表示为

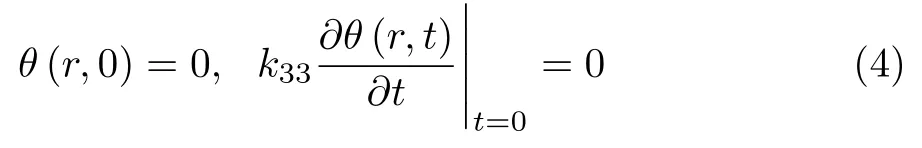
式中,φ0和φ1为某特定值，H(t) 为阶跃函数。

2 频域求解

2.1 状态方程的建立

将式(2) 代入式(1)，整理后得到

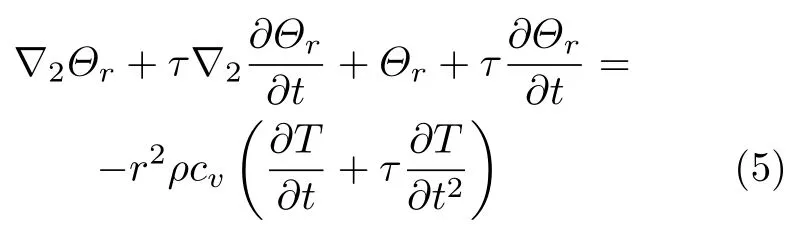
为消除时间变量，将偏微分方程组转化为常微分方程组，引入拉普拉斯变换

将式(2) 和式(5) 利用式(6) 变换后，联合得到状态方程

球壳边界条件式(3) 经过拉普拉斯变换后变为

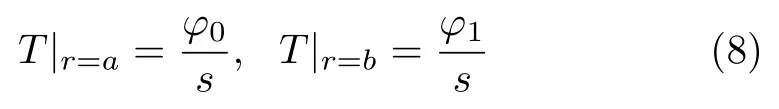
2.2 状态方程的求解

为求解方便，对变量进行无量纲化

其中c33为材料的弹性参数，c为弹性波速，η=ρcv/k33为热黏度系数。为简便考虑，省略后续公式符号中的上标符号“*”。将式(9) 代入式(7)，可得

式中V= [T,Θr]T。由于矩阵M中的元素含有与半径r相关的量，可采用层合模型将其转化为常系数矩阵，当分层的模型足够细时，这种近似方法有足够的精度。将球壳沿厚度方向等分为p层，矩阵中的坐标变量r取为子层中间厚度处坐标值，即r=a+(2i −1)(b −a)/2p，由矩阵理论得式 (10) 的解为

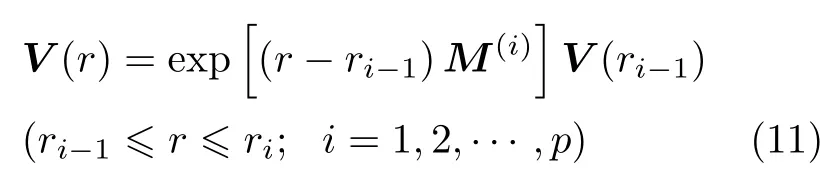
相邻子层间的连续条件要求状态变量连续，由式(11)出发递推可得

为二阶方阵。引入球壳内外温度边界条件式(8)，代入式 (12)，得

从而可求得球壳内表面的热流密度状态量

式中Tij为矩阵T的元素。利用式(11) 可以求得沿径向任意位置的状态量温度值。

对于大部分边界条件, 无法直接将频域解解析为时域解，必须采用近似方法进行拉普拉斯数值反变换[26-29]。本文采用Durbin[26]的傅里叶级数法

其中U为反变换的周期，合理的参数取值为 5αU10，50NUSM5000。

3 时域求解

3.1 分解

将式(9) 代入式(5) 化简后为

由于边界条件式(3)非齐次，不能直接利用分离变量法来求解方程 (16)，因而需要进行边界条件的齐次化，将温度场解分解成两部分：对应非齐次边界条件的解TS(r) 和对应齐次边界条件的解TD(r,t)，即

3.2 稳态解 TS(r)

非齐次边界条件下的热传导边值问题可以表示为

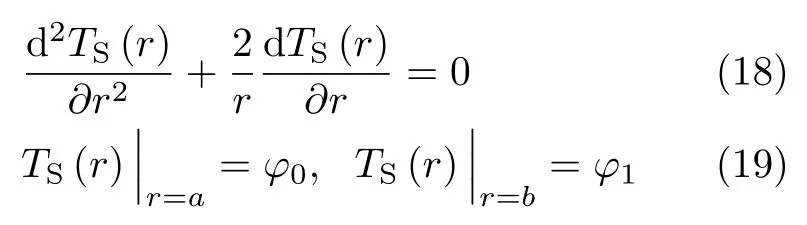
式 (18) 的解为

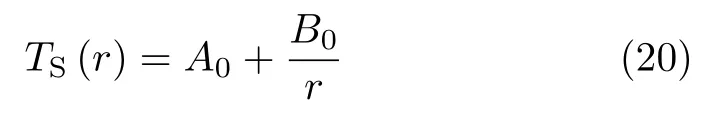
其中A0和B0为待定常数，将式 (20) 代入边界条件式 (19)，得到

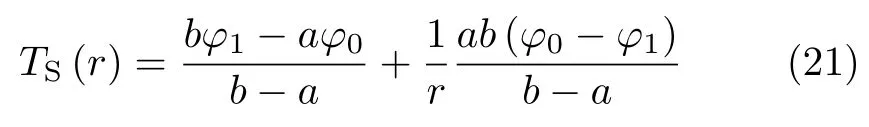
3.3 瞬态解 TD(r)

满足齐次边界条件及初始条件的球对称热传导问题为

假设TD(r,t) =RT(r)L(t)，将其代入式 (22)，从而得到

考虑式(25) 两端只能等于常数−ω2，分解成两个2阶常微分方程

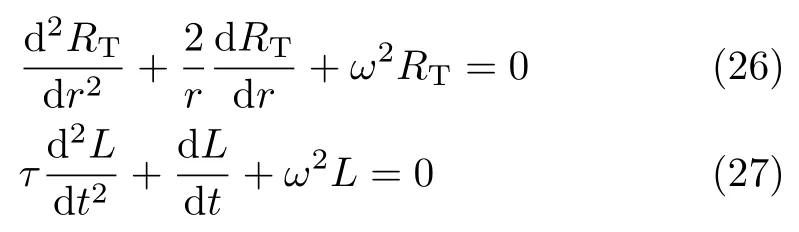
相应的边界条件为

式(26) 为贝塞尔方程，其解析解为

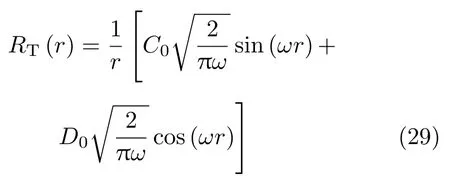
其中C0和D0为待定系数。将式 (29) 代入边界条件式(28)，可以得到

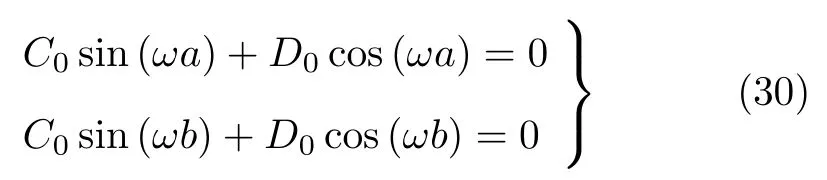
为保证式(30) 存在非零解，系数矩阵行列式必须为零，即

求解上述超越方程，可以得到无穷个特征根ωk(k=1,2,···)，对于任意ωk，式 (29) 的解为

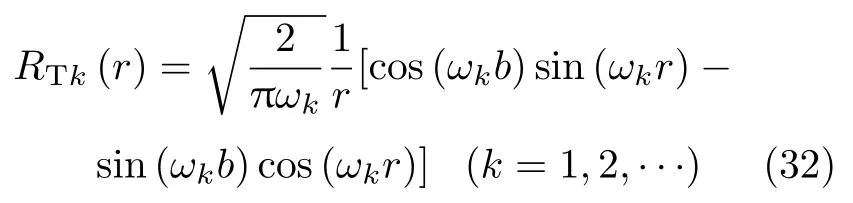
二阶常微分方程(27) 的解为

由初始条件式(24) 第1 式得

对应不同本征值的本征函数RTk(r)和RTj(r)正交性证明推导过程及模值详见文献[30]，这里直接给出模值

利用级数正交展开技术，由式(35) 可得

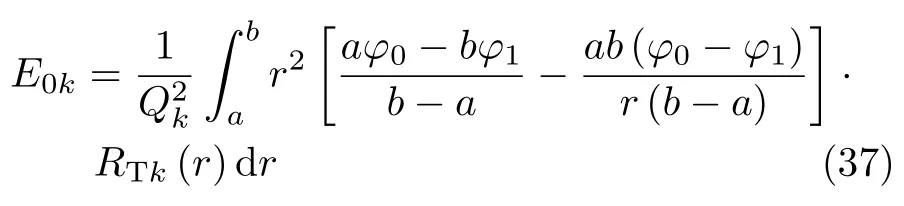
由初始条件式(24) 第2 式得

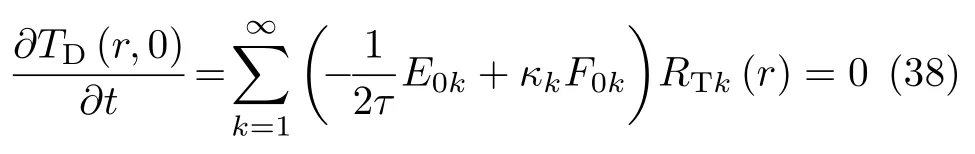
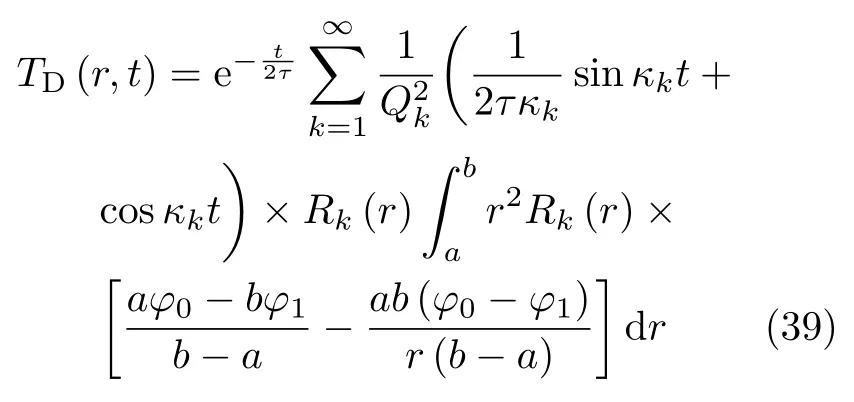
3.4 全解

将稳态解和瞬态解两部分叠加，得到总的温度场

4 算例

为验证本文解的正确性和有效性，将两种方法与文献[31] 计算结果进行对比。球壳无量纲参数为：内半径a= 1，外半径b= 2，波速c1= 1，c2=0.535，ε=0.02。温度边界条件为

求解时，频域法采用层合近似法将球壳沿厚度方向细分60 等分，时域法采用前70 阶特征根，和文献[31] 得到的球壳内表面温度随时间变化的结果吻合得非常好，如图 2 所示，表明本文理论推导和数值计算的正确性。

图2 球壳内表面温度随时间变化

下面以硒化镉球壳受内外温差变化为例，材料参数为：c33= 83.6 GPa,ρ= 5.68 t/m3,k33=12.9 W/(m·K),cv= 0.46×103J·kg/K。无量纲热弛豫时间τ= 0.1，球壳内外径之比a/b取为0.5，内/外表面分别同时突加温升 200◦C/400◦C。图3 为采用频域法所求得对应不同时刻内部温度变化沿着球壳径向分布情况，计算时，将球壳沿厚度方向80 等分。观察后可以发现，内外表面热冲击所产生的热波，以无量纲速度向球壳对向传播。在温度波前尚未到达的区域内，温度保持初始温度不变，当热波波前到达某位置，该处形成一个明显的温度阶跃现象，当双向的热波交汇后，球体内部的温度会超过边界处设定的温度。产生的原因在于热传导时间与热驰豫时间相当时，材料的局部热平衡已经不能维持[1]。

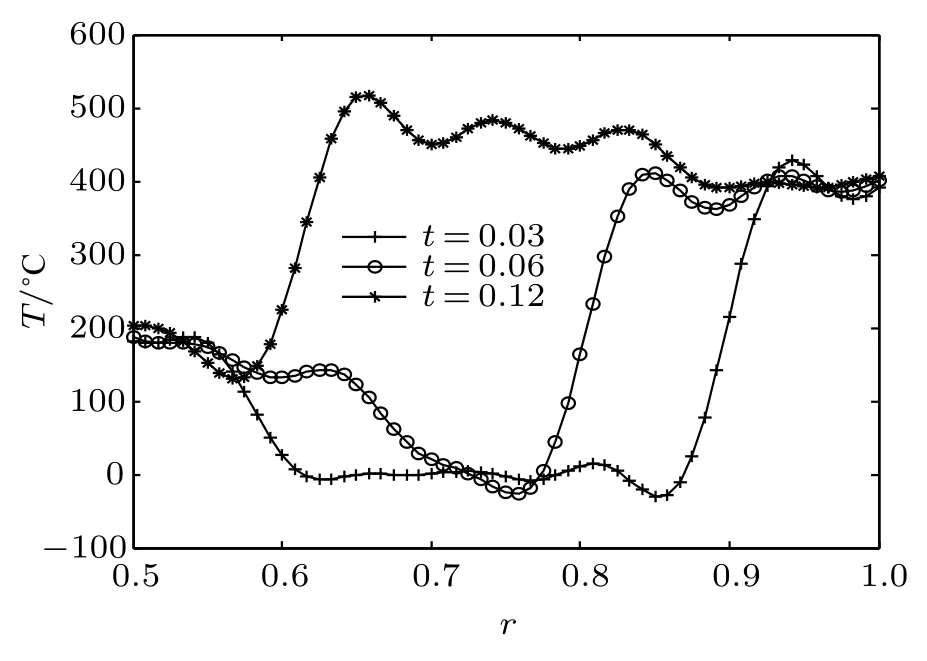
图3 对应不同时间t 温度沿球壳厚度方向变化(频域法)

图4 为时域法求得的结果，计算时采用了前70阶频率。对比图3 和图4 可以看出，两种不同方法所求得的温度分布具有大致相似的结果，表明两种计算方法的有效性。频域法所求得结果不存在明显的波动和阶跃现象，原因为数值反变换近似方法所固有的截断误差和数值震荡所导致；时域方法求解的温度结果存在更明显的阶跃，可以避免拉普拉斯反变换所带来的数值误差，显示其可清晰捕捉热波传播的前沿波阵面，表明采用该方法求解具有更高的精度。