庄照荣 李兴良 陈春刚

1 国家气象中心，北京 100081

2 中国气象局数值预报中心，北京 100081

3 西安交通大学，西安710049

1 引言

经过几十年的发展，变分同化技术趋于成熟，其中在变分分析中背景误差协方差描述得更精细，更接近模式的实际误差状态。背景误差协方差中单一变量的空间相关关系和不同变量间的相关关系直接决定观测信息传播的程度和变量之间的协调性，对分析质量非常重要。在区域模式变分同化方法中背景误差协方差的水平相关假定各向同性，用相关模型来代替，背景误差协方差矩阵的水平变换部分通过递归滤波来实现，递归滤波精度由滤波近似程度决定。

在变分同化方法中通常都采用一阶滤波迭代多次使递归滤波器逐渐趋近于准高斯滤波器（Vandenberghe and Kuo, 1999; 张华等, 2004; 薛纪善和陈德辉, 2008）。Purser et al.（2003a）比较了变分分析中高斯相关模型及其拉普拉斯算子在递归滤波方案中采用一阶到六阶近似滤波效果的差别，指出变分同化方法中可采用一阶近似滤波4 次描述背景误差水平相关，但分析增量不满足观测向水平各个方向的传播都一样（等方），效果明显不如四阶近似滤波1 次，同时指出对于高斯的拉普拉斯算子至少四阶滤波可以获得类似等方的结构。为了提高递归滤波的精度，何光鑫等（2011）、王玉柱等（2014）都在三维变分中采用了高阶递归滤波，研究发现采用四阶近似递归滤波运行1 次的效果明显好于一阶滤波运行四次的结果。

另一方面，背景误差水平相关模型通常采用高斯或者二阶自回归模型来描述，通过递归滤波来实现相关矩阵和向量的乘积（Vandenberghe and Kuo,1999; 薛纪善和陈德辉, 2008）。相关研究指出高斯相关模型在小尺度上的功率谱不足（Vandenberghe and Kuo, 1999），对 小 尺 度 作 用 不 大。Purser et al.（2003b）构造出不同尺度叠加的高斯模型来代表背景误差水平相关模型，这种模型比单一高斯模型能构建更有益、多样化的协方差形状，而且这种模型也更有利于控制相关模型拉普拉斯算子的旁瓣峰值。何光鑫等（2011）也采用尺度叠加高斯相关模型通过四阶递归滤波能在保持大尺度信息的基础上，获得一些中小尺度的信息。吴洋等（2018）也采用多特征尺度的递归滤波器在分析和预报中获得了更多的α 中尺度信息。

在变分同化系统中，通常采用高斯及其叠加模型，或二阶自回归模型描述水平相关关系，但对不同相关模型的具体性质分析较少。本文分别从时空域和频谱空间来揭示各类相关模型的特征，同时研究三种不同的相关模型在我国自主研发的全球和区域同化预报系统三维变分分析（GRAPES-3DVar）（张华等, 2004; 庄世宇等, 2005; 薛纪善和陈德辉,2008）中的应用情况，从本质上说明不同相关模型对分析增量结构及对频谱空间不同尺度上信息的影响。

2 水平相关模型性质

本节分别从时空域和频谱域空间分析高斯相关模型（Gauss）、二阶自回归相关模型（Soar）及尺度叠加高斯模型（Supergauss）的空间和频谱分布特征。

2.1 高斯与二阶自回归相关模型

2.1.1 时空域空间

若高斯G (r)和 二阶自回归相关模型S (r)分别为

其中，r 为一维空间两点间的距离，L 为固定水平相关尺度，高斯和二阶自回归相关模型就是随距离变化的模型（图1a）。这里L 都取500 km，从图1a中可以看出随着距离的增加，两点之间的相关随指数关系下降，采用同样的水平相关尺度时，二阶自回归相关模型下降幅度更缓慢，观测信息会传播更远。在GRAPES-3DVar 分析中分析变量的背景误差水平相关采用公式（1）或（2）来描述，而风场（u, v）的水平相关关系和水平相关模型的拉普拉斯算子有关，相关内容见第3 节，公式（1）和（2）的拉普拉斯算子为

按照Daley（1991）一维的水平相关尺度 L在两种模型中可分别定义为

在变分分析中水平相关尺度一般采用观测余差方法（Hollingsworth and Lönnberg, 1986; Lönnberg and Hollingsworth, 1986; Franke, 1999; Xu et al.,2001; 庄照荣等, 2006b）或NMC 方法（Parrish and Derber, 1992; Dee and Gaspari, 1996; Ingleby, 2001;王金成等, 2014; 王亚华等, 2017; 庄照荣等, 2019）统计获得。

2.1.2 频谱域空间

从时空域空间来看，水平相关模型的形状影响观测信息传播的远近和大小；而从频谱域空间看，可知不同相关模型在各个尺度上的影响。对公式（1）和（2）进行傅立叶变换，高斯和二阶自回归模型的谱响应函数（象函数）为

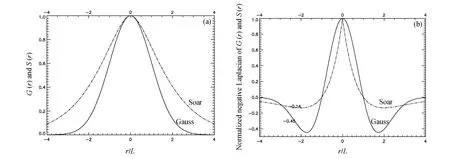
图1 （a）高斯（Gauss）和二阶自回归（Soar）相关模型及其（b）归一化的负拉普拉斯算子。r 为两点间的距离，L 为固定水平相关尺度Fig.1 (a) Gaussian and second-order autoregressive correlation models and (b) their normalized negative Laplacian. r represents distance of two point, L indicates horizontal correlation length

从图2b 以看出，二者拉普拉斯的谱响应函数在低频时（ kL <0.2）都略小，在0.2< kL<3 之间时较大；而在 kL>3 部分，高斯模型的拉普拉斯谱响应函数下降较快，二阶自回归的下降平缓，二阶自回归的拉普拉斯谱响应函数在较小尺度的功率谱远远大于高斯模型的。

2.1.3 泰勒展开

当水平相关模型用递归滤波来描述时，利用了泰勒展开近似来简化运算。高斯和二阶自回归模型的泰勒展开分别为

比较（10）和（11）式可以看出，在泰勒展开的一阶近似中，高斯模型和二阶自回归模型等价。

2.2 尺度叠加的高斯模型

二阶自回归模型作为背景误差水平相关模型，在时空域空间其拉普拉斯的分布和频谱空间中小尺度上功率谱的表现上都优于高斯模型，但是在递归滤波的实施上，由于递归滤波精度不够，造成风场分析增量为非各向同性（见4.2 节）。考虑多元正态分布满足可加性，因而不同尺度高斯模型线性组合也满足正态分布，可利用高斯模型的可加性进行递归运算。通过多尺度高斯模型的叠加来描述背景误差水平相关，缓解采用单一高斯模型作为水平相关模型存在的问题。

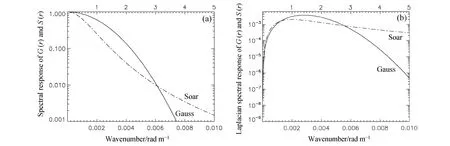
图2 （a）高斯和二阶自回归相关模型的谱响应函数及其（b）拉普拉斯算子的谱响应函数Fig.2 (a) Spectral response functions of Gaussian and second-order autoregressive correlation models and (b) their Laplacian spectral response functions

2.2.1 时空域空间则尺度叠加高斯模型的拉普拉斯也是高斯模型拉普拉斯尺度叠加后的平均，同样利用傅立叶变换线性性质，它们的谱响应模型也对应各种尺度高斯模型及其拉普拉斯谱响应模型的平均。图3 为采用350 km、500 km、850 km 的水平相关尺度的高斯相关模型及其归一化的拉普拉斯算子，可以看出随着水平相关尺度从850 km 降低到350 km，高斯及其拉普拉斯模型相关模型形状更窄，说明观测信息传播的更近。当采用以上三种尺度进行尺度叠加后，尺度叠加的高斯模型在近距离可以保持尺度为500 km 的高斯模型/高斯拉普拉斯算子的形状，而在远距离下降趋势都减缓（Supergauss 表示尺度叠加的高斯模型）。由于不同水平相关尺度的高斯模型拉普拉斯的旁瓣峰值位置不同，因而尺度叠加后的旁瓣峰值也明显变小，三种尺度叠加的高斯模型的归一化负拉普拉斯旁瓣峰值降低到−0.24，而且负拉普拉斯的旁瓣峰值可以采用不同的高斯模型组合进行调节。本文将利用尺度叠加的高斯模型减小旁瓣峰值对风场分析增量的影响，减小在观测稀疏区域对后续模式积分不利的虚假增量。

2.2.2 频谱域空间

对尺度叠加的高斯模型（12）式进行傅立叶变换，由傅立叶变换的线性性质，其谱响应函数为

从尺度叠加高斯模型的谱响应函数可以看出（图4a），当水平相关尺度从850 km 降低到350 km，虽然时空域空间观测信息传播的更近，但是在高频部分的功率谱急剧增加，说明水平相关尺度降低后，高频部分的能量更强。尺度叠加的高斯模型谱响应函数在低频部分能和相关尺度为500 km 的高斯模型功率谱相当，同时在高频部分的功率谱比单一500 km 高斯模型的功率谱增加很多。对于尺度叠加高斯模型的拉普拉斯算子的谱响应函数也是同样的结论（图4b）。

3 水平相关模型在变分中的应用

3.1 GRAPES 三维变分分析

GRAPES 区域三维变分分析（GRAPES-3DVar）是求控制变量的目标函数（J）达到极小时的分析场（薛纪善和陈德辉, 2008; 薛纪善等, 2012）：

图3 （a）不同尺度的高斯相关模型和尺度叠加的高斯模型及其（b）归一化的负拉普拉斯算子。G350、G500 和G850 分别表示相关尺度为350 km、500 km 和850 km 的高斯相关模型；Supergauss 表示以上三种尺度叠加的高斯模型Fig.3 (a) Gaussian correlation models of different scales, Supergauss correlation model and (b) their normalized negative Laplacians. G350, G500, and G850 indicate Gaussian correlation models with horizontal correlation length of 350 km, 500 km and 850 km, respectively; Supergauss represents superposition of Gaussian components with the three horizontal correlation lengths

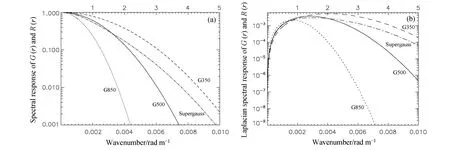
图4 （a）不同尺度的高斯相关模型和尺度叠加高斯模型的谱响应函数及其（b）拉普拉斯算子的谱响应函数Fig.4 (a) Spectral response functions of Gaussian correlation models with different scales, Supergauss correlation model and (b) their Laplacian s pectral response functions

其中，V 为正交垂直模，S 为垂直模的方差向量，R 为背景误差水平相关矩阵。背景误差水平相关矩阵与某个向量的乘积可用递归滤波来逼近（薛纪善和陈德辉, 2008; 何光鑫等, 2011）：

RF为一次向前一次向后的递归滤波，R 可以通过N次向前/向后的递归滤波来逼近。在GRAPES-3DVar 系统中，背景误差协方差采用NMC 方法统计，水平相关关系采用高斯模型来描述，背景误差协方差水平变化部分采用一阶递归滤波算法，根据高斯模型的谱响应与一阶递归滤波的振幅响应因子的关系来确定滤波系数，滤波迭代次数为10。

3.2 递归滤波方案

可知：

研究表明四阶递归滤波运行1 次的滤波效果明显好于一阶滤波运行4 次的结果（Purser et al.,2003a; 何光鑫等, 2011; 王玉柱等, 2014），但考虑到高阶递归滤波的计算量和内存需求，目前GRAPES 区域3DVar 系统中采用一阶滤波运行10次来逼近水平相关矩阵的运算。

由于二阶自回归模型不具有高斯模型可分解的性质，因而一阶滤波中只向前向后运行一次，即滤波次数N 为2。

对于尺度叠加的高斯相关模型，利用傅立叶变换线性的性质，可采用多次不同尺度的递归滤波运算叠加来实现。

在二维空间，二维各向同性的高斯滤波器相当于两个独立方向高斯滤波器的乘积（Purser et al.,2003a; 何光鑫等（2011）），即：

3.3 动力场变量之间的水平相关

在大气中不同变量之间的相互关系也隐含在背景误差协方差之间，研究最多的为风压场之间的关系，例如，动力场和质量场的平衡关系可以用平衡方程来描述（庄照荣等, 2006a; 王瑞春等, 2015a），也可以用动力与统计相混合的平衡约束方案来反映（王瑞春等, 2015b）。对于分析变量的流函数、非平衡势函数与模式变量风场（u, v）的误差协方差之间关系关注较少，这一节主要研究这两种动力场变量之间的背景误差水平相关关系。

由（37）式可知，一维西风的背景误差协方差由分析变量采用的相关模型拉普拉斯算子的形状决定。由于GRAPES-3DVar 采用了流函数和非平衡的势函数作为分析变量，风场（u, v）观测的传播方式符合分析变量相关模型的拉普拉斯算子的分布（图1b）。因而用相关模型描述分析变量背景误差的水平相关系数时，不仅要求相关模型本身能匹配实际分析变量的水平相关，相关模型的拉普拉斯算子也应该有合理的结构来描述风场之间的相关关系。

4 数值分析试验

4.1 试验设置

本文分别把高斯、二阶自回归，以及尺度叠加的高斯模型作为GRAPES-3DVar 背景误差水平相关模型进行了单点观测试验。试验采用的GRAPES-3DVar 为全球和区域一体化的分析系统，试验水平分辨率为10 km（除湿度外，采用高斯和二阶自回归相关模型时，水平相关尺度都设为500 km），分析变量为流函数、非平衡势函数、非平衡无量纲气压和湿度。当采用尺度叠加的高斯模型时，相关尺度为850 km、500 km、350 km；对于湿度变量，当采用高斯和二阶自回归相关模型时，水平相关尺度都设为200 km，当采用尺度叠加的高斯模型时，相关尺度为350 km、200 km、150 km。三组试验都采用一阶递归滤波，其中高斯及尺度叠加的高斯相关模型的递归滤波次数为10，二阶自回归相关模型的递归滤波次数为2。三组试验中其他设置都完全一致。依据3DVar 分析中的背景误差相关关系（公式32、34、35），观测风场的信息可影响到无量纲气压场和风场的其他格点，气压观测信息影响风场和质量场的其他格点，湿度变量为单变量分析，依据公式（31），湿度观测只影响湿度分析。

4.2 分析增量

第一组为单点u 风场观测分析试验，以u 新息增量（观测减去背景场）为主， v新息增量为0，分析后无量纲气压、 u、 v 风场的分析增量如图5 所示，比较第一列和第二列可以看出对于同样的水平相关尺度，二阶自回归相关模型把观测信息传播得更远。同时也可以看出采用Gauss 相关模型时， u分析增量在距观测点南北方向5 度以外都有较大负增量（图5a2），而Soar 试验基本没有显示出负分析增量（图5b2），尺度叠加高斯模型的负分析增量比采用单一高斯相关模型要小（图5c2）。从图5b2中也可以看出，由于Soar 相关模型只采用了一阶滤波，分析增量各向异性，分析增量结构相似于Gauss 拉普拉斯函数采用2 阶滤波运行一次的结果（Purser et al., 2003a；图3a）。从图6a 的归一化u分析增量（110°E 切线方向）可以明显看出不同相关模型对风场的影响，与图1b、图3b 相关模型的二阶导数结构类似，Gauss 模型的风场负增量最大，Soar 模型的风场负增量最小，采用3 种水平相关尺度高斯模型叠加的分析风场负增量比单一尺度高斯模型的有所减小。

第二组为单点相对湿度观测分析试验，由于比湿与其他变量不相关，因而单点湿度观测的分析增量直接显示出相关模型本身的空间结构（图5 第四行），从归一化湿度分析增量（110°E 切线方向）可以看出湿度分析增量结构由图1a 和图3a 的相关模型的结构决定（图6b）。

第三组单点v 风观测分析试验，v 新息增量为主，u新 息增量为0，分析后无量纲气压、 u、 v风场的分析增量如图7 所示。比较第一列和第二列也可以看出对于同样的水平相关尺度，二阶自回归相关模型把观测信息传播得更远。同时也可以看出采用Gauss 相关模型时， v分析增量在距观测点东西方向5 度以外都有较大负增量（图7a3），而Soar 试验基本没有显示出负分析增量（图7b3），尺度叠加高斯模型的负分析增量比采用单一高斯相关模型要小（图7c3）。从图7b3 中也可以看出，由于Soar 相关模型只采用了一阶滤波， v分析增量各向异性，其分析增量结构相似于第一组试验中Soar的u 分析增量的结构。

图5 单点u 风场和湿度观测分析试验的分析增量：Gauss（左）；Soar（中）；Supergauss（右）。第1～4 行分别为无量纲气压（×10−6）、u 风场（单位：m s−1）、v 风场（单位：m s−1）、比湿（单位：10−4 kg kg−1）Fig.5 Analysis increments for single u-component wind and humidity observation: Gauss (left); Soar (middle); Supergauss (right). The row 1–4 indicate nondimensional pressure (×10−6), u-component (units: m s−1), v–component (units: m s−1), specific humidity (units: 10−4 kg kg−1), respectively

图6 110°E 处（a）u 风场和（b）比湿归一化的分析增量Fig.6 Normalized analysis increment for (a) u-component and (b) specific humidity at 110°E

第四组试验为单点气压观测分析试验，分析后无量纲气压、 u、 v风场的分析增量如图8 所示。从图8 可以看出，三种相关模型方案的分析增量结构相似，只是二阶自回归相关模型把观测信息传播得更远。单点气压观测分析中，无量纲气压分析增量的结构由相关模型的结构决定，而风场分析增量的结构受质量场和风场的相关关系影响。

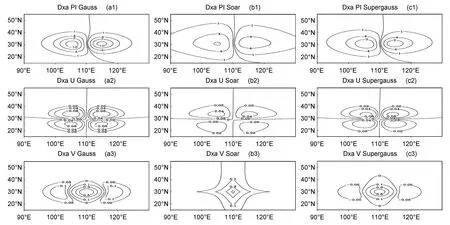
图7 同图5，但为单点v 风场观测分析试验的分析增量Fig.7 As in Fig.5, but for analysis increments for single v-component wind observation

图8 同图5，但为单点气压观测分析试验的分析增量Fig.8 As in Fig.5, but for analysis increments for single pressure observation

由上可知，在u/ v单点观测分析试验中，三种相关模型的u/ v分析增量差别最大，结合上两节分析，Gauss 模型下的u/ v分析增量中距观测远处的负增量偏大较多，这种负增量结构和相关模型的拉普拉斯算子有关，对于Gauss 模型不能调节负增量的大小；Soar 模型下的u/ v分析增量结构明显各向异性，会造成分析增量的不连续；Supergauss 模型下的u/ v分析增量中距观测远处的负增量比Gauss 试验的小，而且采用不同相关尺度组合的尺度叠加高斯相关模型可以调节负增量的大小，因而在这3 种相关模型中，从分析增量结构来看，Supergauss 相关模型在GRAPES-3DVar 中应用最有优势。

4.3 分析增量的功率谱

从上节可以看出，当同化单点湿度或气压观测时，在时空域湿度或无量纲气压的分析增量分布与相关模型结构相一致；当同化单点u/ v风场观测，u/ v分析增量分布也明显和相关模型的拉普拉斯算子结构相关，此节从频谱域空间研究分析增量的功率谱分布。文中对单点观测分析试验的分析增量采用二维离散余弦转换（2D-DCT: Discrete Cosine Transform）方法进行谱分解（Denis et al., 2002; 郑永骏等, 2008; 庄照荣等, 2018），获得分析增量的功率谱，研究不同相关模型方案的分析增量功率谱的分布特点。

若定义天气尺度波为2000 km 以上，次天气尺度波为669～2000 km（龚建东, 2007），中尺度波在669 km 至几十公里，则从图9 的u 单点观测和湿度单点观测试验的分析增量功率谱可以看出，3种相关模型的分析增量功率谱大值都集中在波长1000 km 以上的天气尺度和次天气尺度波动上。Gauss 相关模型的四个分析增量取对数后的功率谱基本从1～6 波（波长从1710～8459 km）都逐步增大，然后在7～21 波（波长从513～1476 km）对数功率谱又随着波数的增加呈现快速下降的趋势，随后在22 波以上（波长<490 km）随着波数增加，对数功率谱缓慢下降。比较不同模型的分析增量功率谱，对于无量纲气压，可以看出在965 km 以上的天气尺度和次天气尺度部分，Soar 分析增量功率谱略小于Gauss 的，Supergauss 分析增量功率谱介于二者之间；在965 km 以下的尺度部分，Gauss的分析增量功率谱快速下降，并逐渐远远小于Soar 的分析增量功率谱，Supergauss 的分析增量功率谱则介于Gauss 和Soar 之间，在965 km 以下的次天气尺度和中尺度Supergauss 的分析增量功率谱比单一Guass 模型的有所增加（图9a）。对于比湿，在416 km 以上，Gauss 模型的分析增量功率谱较大，Soar 模型的分析增量功率谱略小，Supergauss模型的功率谱也介于Gauss 和Soar 模型的之间。在416 km 以下的中尺度部分，Soar 模型的功率谱也大于Gauss 的，Supergauss 的功率谱比Gauss 模型的略微增加（图9b）。对于风场，不同相关模型的影响最大，从图9c、d 可以看出，在669 km以下的中尺度部分，Gauss 模型的分析增量功率谱远远小于Soar 的，说明采用Gauss 模型描述背景误差水平相关使中尺度分析信息不足；而采用3 种相关尺度组合的Supergauss 模型会缓解这种现象，分析增量的中尺度功率谱略有增加（图9c、d），同时也可以看出，Soar 试验的u 分析增量功率谱在所有波段上都明显大于v 分析增量功率谱。

图9 单点u 风场和湿度观测分析试验的分析增量功率谱（单位：m3 s−2）：（a）无量纲气压；（b）比湿；（c）u 风场；（d）v 风场Fig.9 Power spectrum (units: m3 s−2) of analysis increments for single u-component wind and humidity observation: (a) Nondimensional pressure;(b) specific humidity; (c) u-component; (d) v-component

比较3 种相关模型方案，对于单点v 观测的分析增量功率谱分布特点与单点u 观测试验的结论相似，只是功率谱大小有所不同。但是Soar 试验的v分析增量功率谱在所有波段上都明显大于u 分析增量功率谱，这与单点u 观测试验的结果相反（图略）。

从单点气压观测试验的分析增量功率谱（图10）也可以看出，在965 km 以上的天气尺度和次天气尺度部分，Soar 三个变量的分析增量功率谱略小于Gauss 的，Supergauss 分析增量功率谱介于二者之间；在965 km 以下的尺度部分，Gauss 的三个变量的分析增量功率谱快速下降，并逐渐远远小于Soar 的分析增量功率谱，Supergauss 的分析增量功率谱介于Gauss 和Soar 之间。虽然在时空域Guass与Supergauss 方案的分析增量结果相似（图8），但是在965 km 以下的次天气尺度和中尺度，Supergauss 的无量纲气压与风场的分析增量功率谱都比单一Guass 模型的增加非常明显（图10）。

由上可知，分析增量的功率谱随波数的变化由相关模型及其拉普拉斯算子在频谱域空间谱响应模型的功率谱分布决定。目前GRAPES-3DVar 分析的中尺度信息不足和采用的高斯相关模型有关，特别是动力场在中尺度部分分析增量的功率谱远远小于二阶自回归的功率谱。若采用3 种相关尺度叠加或更复杂的高斯模型组合来描述背景误差的水平相关关系可以改善中尺度分析。

5 结论和讨论

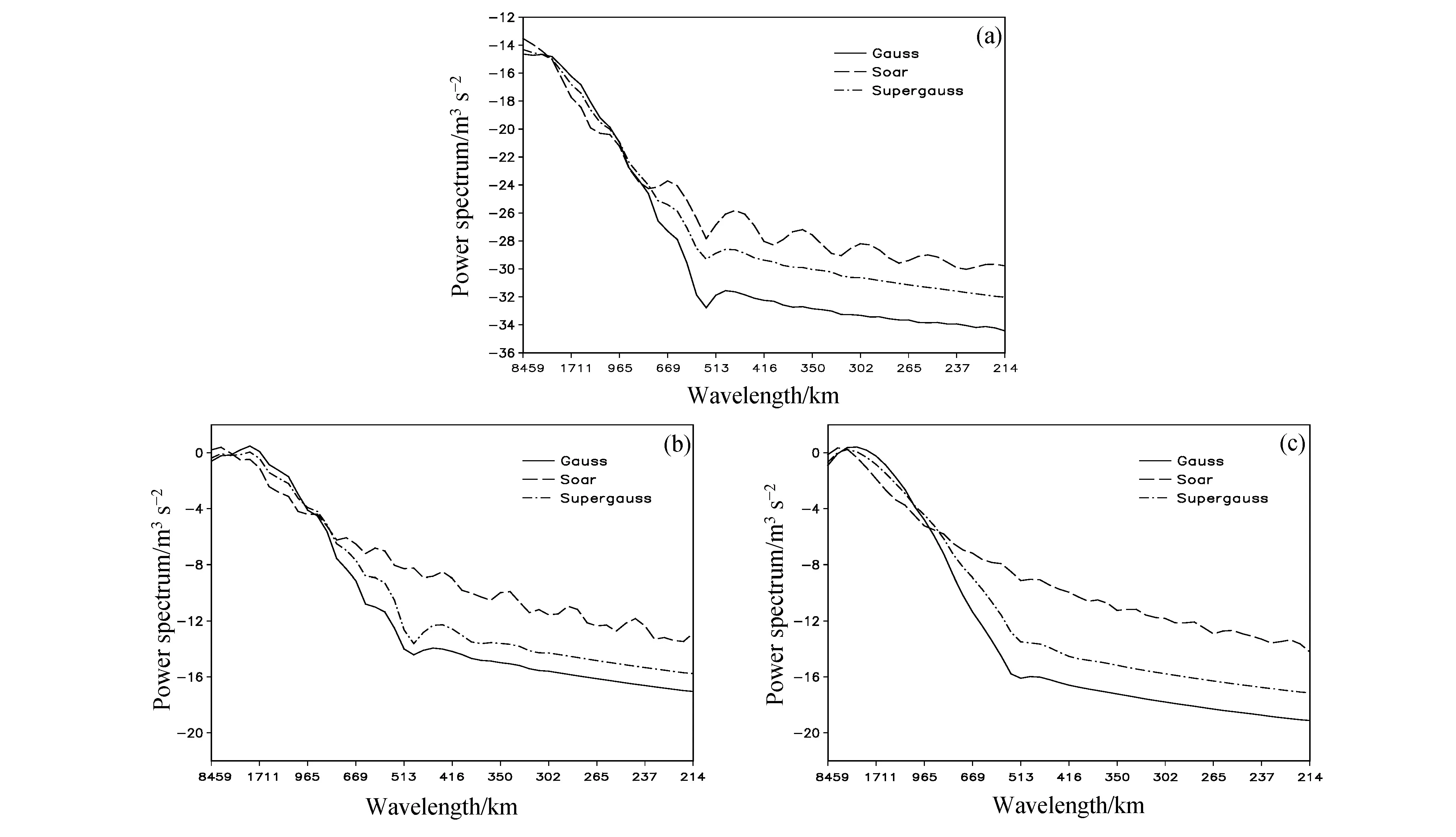
图10 单点气压观测分析试验的分析增量功率谱（单位：m3 s−2）：（a）无量纲气压；（b）u 风场；（c）v 风场Fig.10 Power spectrum (units: m3 s−2) of analysis increments for single pressure observation: (a) Nondimensional pressure; (b) u-component; (c) vcomponent

本文通过比较高斯、二阶自回归以及尺度叠加的高斯模型在时空域和频谱域空间的特征，并把这3 种模型作为水平相关模型应用到GRAPES-3DVar 系统中进行理想分析试验，从本质揭示不同相关模型对分析的影响。本文主要得到以下结论：

（1）采用高斯或二阶自回归模型作为分析变量流函数和非平衡势函数的水平相关模型时，根据动力场之间的水平相关关系，u、v 风场的水平相关关系与Gauss 或Soar 的负拉普拉斯算子有关，因而相关模型负拉普拉斯算子的旁瓣峰值信息会影响风场观测的分析质量。

（2）高斯模型作为水平相关模型时，由于其拉普拉斯算子的旁瓣峰值较大，因而造成风场观测负相关较大，距离观测点较远的分析会出现不合理的较大负增量信息；同时高斯模型及其拉普拉斯算子在中小尺度上功率谱下降太快，也会导致分析场的中小尺度信息不足。

（3）二阶自回归模型作为水平相关模型时，其拉普拉斯算子的旁瓣峰值较小，因而风场观测的负相关信息最小，并且二阶自回归模型及其拉普拉斯算子的谱响应函数在中小尺度上功率谱较大，有利于高分辨率模式的中小尺度分析。但是在GRAPES-3DVar 的递归滤波实施中容易造成不合理的各向异性分析增量。

（4）当高斯相关模型的水平相关尺度降低时，高频部分的谱响应函数会增加，因而观测资料的传播会包含更多的中小尺度能量，分析增量的中小尺度信息会增加。

（5）尺度叠加的高斯模型作为水平相关模型时，不仅缓解单一尺度高斯模型拉普拉斯算子负相关较大问题，同时也增加分析增量的中小尺度能量，尺度叠加的高斯模型方案在递归滤波中也较容易实施。因而，在3 种方案中尺度叠加的高斯模型是GRAPES-3DVar 中描述背景误差水平相关的最佳方案。

本文研究不同水平相关模型对分析的影响，分析中分析变量为流函数和非平衡势函数，当观测资料分布不均匀时不同相关模型的影响会更加显著，特别是其拉普拉斯算子的旁瓣峰值的大小可能造成稀疏观测区较大的风场分析偏差。文中只给出3 种不同尺度叠加的高斯相关模型的分析结果，若采用更多不同相关尺度高斯模型组合即超级叠加高斯模型，用尺度参数控制模型及其拉普拉斯算子的传播程度和在不同尺度上谱能量的大小，使相关模型能准确描述分析变量流函数和非平衡势函数的水平相关关系，也使相关模型拉普拉斯算子的结构符合实际风场的水平相关关系，也许会获得更合理的分析增量。后续工作将统计模式预报场的水平相关系数，考察风场变量的实际负相关程度，重新调整尺度叠加的相关模型参数，进行实际观测资料同化和预报试验。另外，当分析中的分析变量为u 和v 风场时，水平相关模型直接描述u 和v 风场的水平相关关系，水平相关模型结构需要重新设计来适应于风场变量，而且对分析的影响要重新评估。在高分辨率模式下，还需要通过多尺度同化技术构造不同资料的多尺度空间观测误差和背景误差协方差信息，通过多次不同尺度同化，实现不同空间尺度观测信息的快速有效融合，此时如何设计适合多尺度同化方案的水平相关模型，在有效同化不同尺度观测信息的基础上，还能保证计算效率是需要进一步研究的内容。

本文研究内容基于三维变分分析系统，在当前流行的混合变分分析系统中，背景误差协方差采用气候统计的静态结构和集合统计的随天气形势演变的动态结构（Wang et al., 2008a, 2008b, 2013; Hamill and Snyder, 2000; 马旭林等, 2014, 2015; Chen et al.,2015），静态的背景误差协方差权重相对动态的较小，因而协方差模型的作用也会相对减弱（Bédard et al., 2020）。此外，在集合同化以及集合变分的同化方法中，天气形势依赖的背景误差协方差取代气候态的背景误差协方差，避免了对背景误差协方差进行模型化。例如，集合卡尔曼滤波（EnKF）（Evensen, 1994, 2003; Houtekamer and Mitchell,1998, 2001; 庄 照 荣 等, 2011a, 2011b; Houtekamer and Zhang, 2016）、集 合 平 方 根 滤 波（EnSRF）（Whitaker and Hamill, 2002）以及集合卡尔曼平滑（EnKS）（Evensen and van Leeuwen, 2000）等集合同化算法都采用集合样本获得流依赖的背景误差协方差，并且获得一组集合分析。在集合变分同化方法中，En4DVar 需要对预报模式进行切线性化（Bishop and Hodyss, 2011; Clayton et al., 2013;Gustafsson and Bojarova, 2014），而4DEnVar 可以避免对预报模式的切线性和伴随计算（Liu et al.,2008, 2009; Liu and Xiao, 2013; Wang and Lei, 2014;Kleist and Ide, 2015），但以上的集合变分同化方法只能获得单一分析。在变分分析和集合分析的基础上衍生出许多同化方法，总的来说四维同化优于三维同化，混合方法比纯粹的变分、集合或者集合变分方案更趋向于获得质量更高的分析（Bannister,2017）。