王 浩，刘沁玲，李伟东**

(1. 云南大学 附属中学，云南 昆明 650091；2. 云南大学 数学与统计学院，云南 昆明 650504)

背包问题是经典的组合优化问题之一[1]，在云计算、边缘计算、区块链、人工智能和流数据处理[2-6]等领域有着广泛的应用. 其中，多背包问题的研究成果最为丰富，其定义如下：给定n个物品的集合A={a1,a2,···,an}和m个背包的集合B={b1,b2,···,bm}.每个物品aj∈A的大小为sj，价值为pj；每个背包bi∈B的容量为Ci. 目标为寻找物品子集A′⊆A，在不超过背包容量的情况下将A′中的所有物品放入背包，使得A′中物品的总价值达到最大.

众所周知，多背包问题是NP-难的，因此需设计近似算法来寻找多背包问题的可行解.设∏是一个最大化的优化问题，I表示该问题的任意一个实例，令 A表示求解优化问题 ∏的一个多项式时间算法，A(I)和 OPT(I)分别表示算法 A求解实例I所得到的可行解的目标函数值和最优解的目标函数值，则算法A的近似比（又称为最坏情形界）[7]定义为

若对任意的实数 ε＞0，算法族 Aε都能得到优化问题 ∏ 的一个 (1-ε)-近似解，并且对于每一个固定的 ε，算法的时间复杂度是关于实例I大小的多项式函数，则称算法族 Aε是关于优化问题的一个多项式时间近似方案.

当背包容量相等且物品的大小与价值相等时，Caprara等[8]给出多背包问题的一个多项式时间近似方案. 当背包容量不等且物品的大小与价值相等时，Caprara等[9]给出多背包问题的一个多项式时间近似方案. 当背包容量相等且物品的大小与价值无关时，Kellerer[10]给出多背包问题的一个多项式时间近似方案.当背包容量不等且物品的大小与价值无关时，Chekuri等[11]给出多背包问题的一个多项式时间近似方案；Jansen[12-13]给出了运行时间更低的多项式时间近似方案，当前的最佳结果为运行时间为poly(n)的多项式时间近似方案；Jansen等[14]证明了多背包问题不存在运行时间为+poly(|I|) 的多项式时间近似方案，这里的 poly(|I|)是指关于 |I| 的多项式函数.

同时，公平分配问题也是经典的组合优化问题之一，并在最近几年受到了广泛的关注. 其定义如下：给定n个物品的集合和m个无容量限制的背包的集合，每个物品aj的价值为pj，将物品放入背包，使得背包的最小收益尽可能地大，这里背包的收益是指放入该背包物品的价值之和. 当物品放入不同背包的价值相等时，Woeginger[15]给出了一个多项式时间近似方案. 当物品放入不同背包的价值相等且具有等级约束时，Li等[16]给出了一个多项式时间近似方案. 当物品放入不同背包的价值不等时，Bezakova等[17]证明了公平分配问题不存在近似比大于的近似算法；Asadpour等[18]给出了公平分配问题的一个近似算法. 黄彦等[19]讨论了特殊网络中带惩罚的鲁棒公平分配问题.

实际上，背包的容量通常有限，因此，带背包约束的公平分配问题应运而生. 其定义如下：给定n个物品的集合和m个背包的集合，每个物品aj的大小为sj，价值为pj；每个背包bi∈B的容量为Ci. 目标为寻找物品子集A′⊆A，在不超过背包容量的情况下将A′中的所有物品放入背包，使得背包的最小收益尽可能地大. 当背包容量相等且物品的大小与价值相等时，Caprara等[8]等给出带背包约束的公平分配问题的一个近似算法，并证明了该问题不存在近似比大于的多项式时间算法. Li等[20]给出带二部图和背包约束的公平分配问题的一个近似算法，并证明了该问题不存在近似比大于的多项式时间算法.

本文研究了物品的价值全为 1 时的带背包约束的公平分配问题，称之为带背包约束的基数公平分配问题，分别对背包容量相等和不等的情形，给出了近似比的下界和几乎最佳的近似算法. 本文结构如下：第1节描述带背包约束的基数公平分配问题；第2节给出背包容量相等情形下，带背包约束的基数公平分配问题近似比的下界和一个多项式时间近似算法；第3节给出背包容量不等情形下，带背包约束的基数公平分配问题近似比的下界和一个多项式时间近似算法；第4节对全文进行了总结，并指出未来的研究方向.

1 问题描述

带背包约束的基数公平分配问题定义为：给定n个物品的集合A={a1,a2,···,an} 和m个背包的集合B={b1,b2,···,bm}，其中物品aj∈A的大小为sj，背包bi∈B的容量为Ci.寻找一个物品的集合A′⊆A，将A′中的物品全部装入这m个背包里，即找到A′的一个完全划分，使得

这里Si表示放入背包bi中的物品集合. 目标函数为最大化背包中装入的最小物品数, 即

引入0-1变量xij，这里xij=1当且仅当可行解中物品aj放入背包bi， 则带背包约束的基数公平分配问题的整数规划形式为：

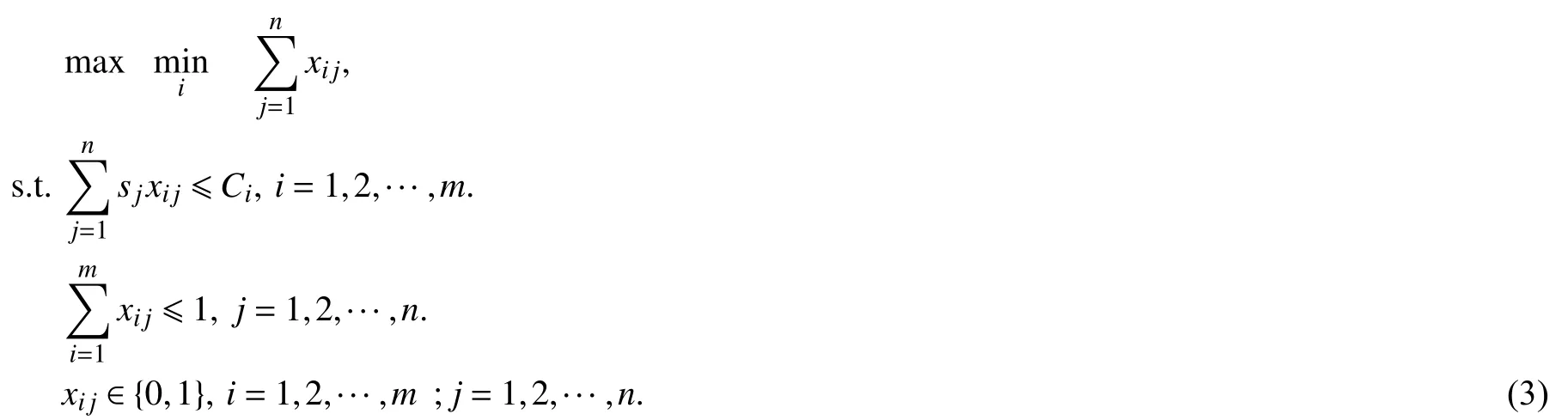
显然，当物品个数n＜m时，至少存在着一个背包没有放入任何物品，最优值为0，则任何可行解都是最优解. 不失一般性，假定n≥m.

定理1当m≤n＜2m时，带背包约束的基数公平分配问题存在多项式时间最优算法.

证明给定带背包约束的基数公平分配问题的一个实例I=(A,B,s,C)，当m≤n＜2m时，至少存在着一个背包放入至多一个物品，则最优值为0或1. 构造一个二部图G=(A∪B,E)，这里顶点集A对应物品集A，顶点B对应物品集B，边 (aj,bi)∈E当且仅当物品aj的大小不超过背包bi的容量，即sj≤Ci.

若实例I的最优值为1， 丢掉背包中多余的物品，可以构造出每个背包恰好包含一个物品的最优解.由可行性知，在最优解中， 放入背包bi的物品aj满足 (aj,bi)∈E. 因此， 可以构造二部图G的一个匹配M，这里 (aj,bi)∈M当且仅当在最优解中物品aj放入背包bi.容易验证， 匹配M的基数为m.

若二部图G中存在着一个基数为m匹配M，对每一条边 (aj,bi)∈M⊆E，由G的构造方式知， 物品aj的大小不超过背包bi的容量. 可以构造实例I的一个可行解， 其中物品aj放入背包bi当且仅当(aj,bi)∈M. 容易验证，每个背包中恰有一个物品， 即其目标函数值为1， 这意味着实例I的最优值为1.

因此， 实例I的最优值为1当且仅当二部图G中存在着一个基数为m匹配M. 利用二部图最大基数匹配问题的多项式时间最优算法[21]可以求得实例I的最优解， 即带背包约束的基数公平分配问题存在多项式时间最优算法. 证毕.

定理2当n=mk+l时，这里 0＜l＜m，带背包约束的基数公平分配问题存在一个装入前mk*个物品的最优解， 这里k*表示最优值.

证明对任意一个最优解，若存在一个背包中放入的物品数大于k*，丢弃该背包中下标最大的物品，直到该背包内的物品数恰为k*，可以得到一个至多使用mk*个物品的最优解. 若存在一个背包装有下标大于mk*的物品，可以用一个下标最小的未放入物品进行替换，直到所有背包中装入的物品的下标都不超过mk*.最终可以得到一个装入前mk*个物品的最优解. 证毕.

因此，不失一般性，本文基于如下假设进行讨论.

基本假设n=mk(k≥2)，且存在着一个目标函数值为k的最优解.

2 背包容量相同的情形

本节考虑所有背包的容量均相同的情形. 首先给出k=2 时，带背包约束的基数公平分配问题的一个多项式时间最优算法. 接着通过对3-划分问题的多项式归约，证明带背包约束的基数公平分配问题是+ε不可近似的，这里 ∀ε＞0，除非 P=NP. 最后，基于贪婪思想给出最佳的近似算法.

定理3当所有的背包容量均相同且k=2 时，带背包约束的基数公平分配问题存在多项式时间最优算法.

证明当所有的背包容量均相同时，对i=1,2,···,m，设Ci=C. 给定带背包约束的基数公平分配问题的一个实例I=(A,B,s,C)，当n=2m时，由基本假设知，最优值为2. 构造一个无向图G=(A,E)，这里顶点集A对应物品集A，边 (aj1,aj2)∈E当且仅当物品aj1和aj2的大小不超过背包容量，即sj1+sj2≤C.

给定实例I的一个最优解，易知每一个背包中恰好装有2个物品ai1和ai2，且这2个物品的大小之和不超过背包容量，因此对应的边 (ai1,ai2)∈E. 这意味着，图G=(A,E)中存在一个基数为m的完美匹配. 给定G=(A,E)的任意一个基数为m的完美匹配M⊆E，对每一条边 (ai1,ai2)∈M，由图G=(A,E) 的构造知，对应的物品ai1和ai2的大小不超过C，因此，每一条边对应的2个物品可以放入同一个背包，从而构造出实例I的一个目标函数值为2的最优解. 利用图G的完美匹配算法[21]可以在多项式时间内求出完美匹配M，进而求出实例I的最优解. 因此，带背包约束的基数公平分配问题存在多项式时间最优算法. 证毕.

定理4当所有的背包容量均相同且k≥3 时，带背包约束的基数公平分配问题不存在近似算法，这里 ε＞0 是任意常数.

证明3-划分问题[22]定义为：给定一个有3m个元素的集合Z={z1,z2,···,z3m}，且满足=mB，其中zj为非负整数且满足问集合Z能否被划分为m个子集Z1,Z2,···,Zm，使得每个子集Zi恰好包含3个Z中的元素，且对任意i∈{1,2,···,m}，有

给定3-划分问题的一个实例I，按如下方式构造带背包约束的基数公平分配问题的一个实例τ(I)：m个容量均为C=B的背包b1,b2,···,bm和 3m个物品，对任意的j=1,2,···,3m，实例I中的元素zj对应一个物品aj，其大小为sj=zj.

下面证明3-划分问题的实例I有解的充分必要条件是带背包约束的基数公平分配问题的实例τ(I) 的最优值为 3.

必要性设3-划分问题有解构造实例τ(I) 的一个可行解：对所有i(i=1,2,···,m)，把Zi={zi1,zi2,zi3}中的元素所对应的物品ai1,ai2,ai3放入背包bi之中，此时有

因此该方案可行且每个背包中装有3个物品. 因为实例 τ(I) 中含有3m个物品，m个背包，故实例τ(I)的最优值为 3.

充分性假设实例τ(I) 的最优值为3. 在最优解中，对所有i(i=1,2,···,m)，背包bi中放入3个物品，记为ai1,ai2,ai3.下面构造实例I的一个可行解：对所有i(i=1,2,···,m)，把背包bi中的物品ai1,ai2,ai3所对应的元素zi1,zi2,zi3置于集合Zi中，即. 因为，且sik=zik，所以，故. 又由于

故对所有i(i=1,2,···,m)，=B.因此Z1,Z2,···,Zm为实例I的可行解.

因此，(3-划分)问题的实例I有解当且仅当τ(I) 的最优值为3. 假设带背包约束的基数公平分配问题存在着一个近似算法 A. 若算法 A的输出解的目标函数值为3，则 τ(I) 的最优值为3，这意味着3-划分问题有可行解. 若算法 A 的输出解的目标函数值不超过2，则 τ(I) 的最优值至多为，这意味着3-划分问题无可行解. 这与3-划分问题的NP困难性矛盾. 因此，带背包约束的基数公平分配问题是不可近似的. 证毕.

当n≥3m即k≥3时，可以利用贪婪法的思想对背包进行轮处理. 每一轮中，在本轮未放入物品的背包中，选择一个剩余容量最小的背包，放入一个下标最小的一个物品，直至超过背包容量或者无剩余物品. 对t=1,2,···,和i=1,2,···,m，令表示进行t轮分配后第i个背包中的物品集，表示中的物品的大小之和. 算法的具体描述如下：

贪婪算法

输入：n个物品构成的集合A，物品aj∈A的大小为sj，m个容量均为C的背包构成的集合B.

输出：m个互不相交的物品子集S1,S2,···,Sm.

第1步：令t=1，且对i=1,2,···,m，令

第3步：将物品atm+1,atm+2,···,a(t+1)m依次放入背包b1,b2,···,bm. 若所有物品均能放入相应的背包，对i=1,2,···,m，令，且t←t+1；否则，算法终止，输出i=1,2,···,m.

第4步：若t=k，则算法终止，输出i=1,2,···,m；否则，转第2步.

定理5对任意2个背包bi1和bi2，均有

证明数学归纳法. 当t=1时，结论显然成立. 假设当t′=t-1(t≥2)时成立，即

设在t轮时放入背包bi1和bi2的物品的大小分别为s1和s2，则

下面分2种情况讨论：

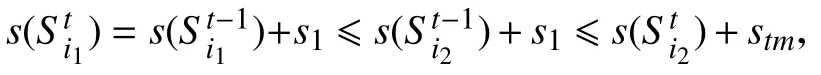
且

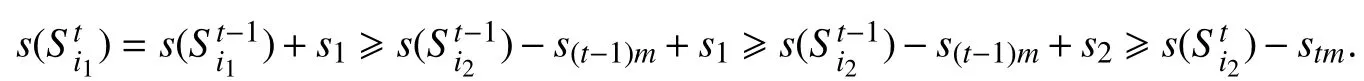
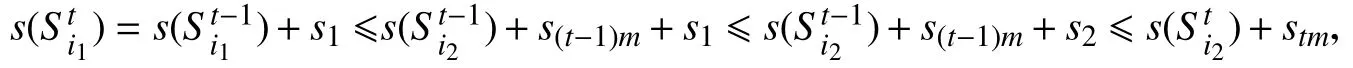
且

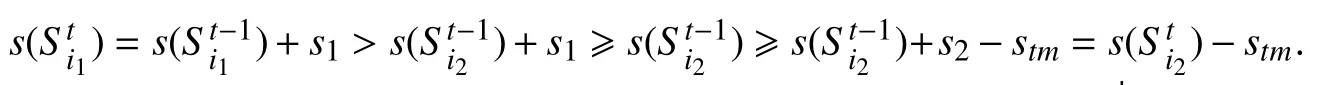
定理6当所有背包的容量均相同且k≥3 时，贪婪算法可以在多项式时间内找到一个目标函数值至少为k-1 的可行解.

证明若算法终止时，t=k或t=k-1，则每个背包中至少装有k-1 个物品，贪婪算法找到一个目标函数值至少为k-1的可行解. 若算法终止时，t=≤k-2，则每个背包中恰好装有个物品. 由算法的选择知，存在一个最小的m0(1≤m0≤m)，使得物品无法放入背包，因此，对i=1,2,···,m0-1 有

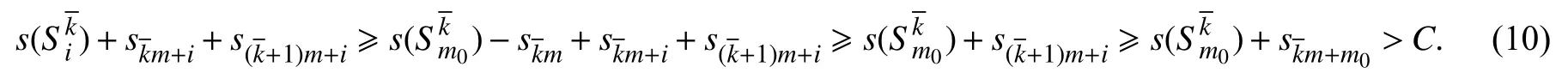
对i=m0+1,m0+2,···,m，由定理5知，

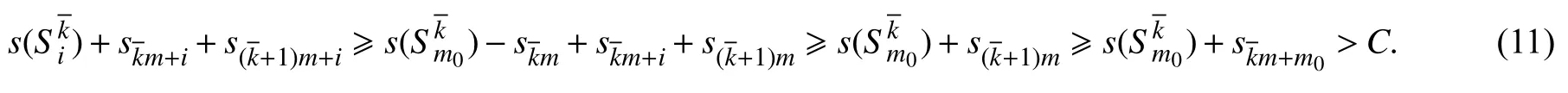
容易验证，贪婪算法至多进行k轮循环，每次循环的计算时间至多O(mlogm). 因此，贪婪算法的运行时间为O(kmlogm).证毕.

算例 1考虑一个m=2，k=3 且C=10的实例，其中6个物品的大小分别为1,1,3,3,4和8. 将物品a1，a2和a6放入背包b1，其余3个物品放入背包b2，可得一个目标函数值为3的最优解. 贪婪算法进行2轮分配后输出一个可行解，其中物品a1和a3放入背包b1，物品a2和a4放入背包b2，从而得到一个目标函数值为2的可行解.

3 背包容量不同的情形

本节讨论背包容量不同的情形. 首先通过对3维数值匹配问题的多项式归约，证明了带背包约束的基数公平分配问题是不可近似的，这里除非 P=NP.最后，分别给出k=2和k≥3 时的几乎最佳近似算法.

定理7当背包的容量不同时，带背包约束的基数公平分配问题不存在近似算法.

证明3维数值匹配问题[22]定义为：给定3个均包含m个元素的集合X={x1,x2,···,xm}，Y={y1,y2,···,ym}，Z={z1,z2,···,zm}，且满足

问集合X∪Y∪Z能否被划分为m个子集A1,A2,···,Am，使得每个子集Ai恰好包含X,Y和Z中各一个元素，且对任意i∈{1,2,···,m}，有

给定3维数值匹配问题的一个实例I，按如下方式构造带背包约束的基数公平分配问题的一个实例τ(I)：对任意的i=1,2,···,m，背包bi的容量Ci=M+B-zi；对任意的j=1,2,···,m，集合X中的元素xj对应一个物品aj，其大小为sj=xj，集合Y中的元素yj对应一个物品am+j，其大小为sm+j=M+yj，这里M是足够大的常数.

下面我们证明3维数值匹配问题的实例I有解的充分必要条件是带背包约束的基数公平分配问题的实例 τ(I) 的最优值为2.

必要性设3维数值匹配问题有解A1={x(1),y(1),z1}，A2={x(2),y(2),z2},···，Am={x(m),y(m),zm}，这里zi包含在集合Ai中，则对i=1,2,···,m，有x(i)+y(i)+zi=B.构造 τ(I) 的一个可行解：对所有i(i=1,2,···,m)，将Ai中的元素所对应的物品a(i)和am+(2)放入背包bi，此时有

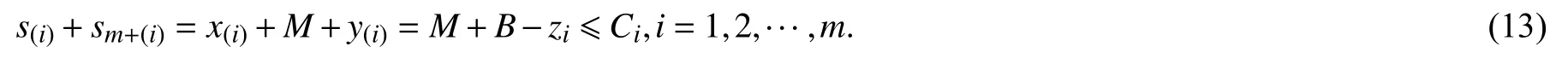
因此该方案可行且每个背包中装有2个物品. 因为共有 2m个物品,m个背包, 故实例 τ(I) 的最优值为2.

充分性假设实例 τ(I) 的最优值为2. 对所有i(i=1,2,···,m)，由实例 τ(I) 的构造方式知，背包bi放入的2个物品分别属于物品集 {a1,a2,···,am} 和 {am+1,am+2,···,a2m}，记为a(i),am+(i).下面构造实例I的可行解：对所有i(i=1,2,···,m)，将背包bi中的物品a(i),am+(i)所对应的元素x(i),y(i)和背包bi所对应的元素zi置于集合Ai中，即Ai={x(i),y(i),zi}.对所有的i=1,2,···,m，因为s(i)+sm+(i)≤Ci=M+B-zi，所以x(i)+y(i)+zi≤B.又由于

故对所有i(i=1,2,···,m)，x(i)+y(i)+zi=B.因此A1,A2,···,Am为实例I的一个可行解.

因此，3维数值匹配问题的实例I有解当且仅当 τ(I) 的最优值为2. 假设带背包约束的基数公平分配问题存在着一个近似算法 A.若算法 A的输出解的目标函数值为2，则 τ(I) 的最优值为2，这意味着实例I有可行解. 若算法 A 的输出解的目标函数值不超过1，则τ(I) 的最优值至多为，这意味着实例I无可行解. 这与3维数值匹配问题的NP困难性矛盾. 因此，带背包约束的基数公平分配问题是不可近似的. 证毕.

定理8当背包的容量不同且k=2 时，可以在多项式时间内找到带背包约束的基数公平分配问题的一个目标函数值至少为 1 的可行解.

证明给定带背包约束的基数公平分配问题的一个实例I=(A,B,s,C)，当k=2 时，由基本假设知，最优值为2. 构造一个二部图G=(A∪B,E)，这里顶点集A和B分别对应物品集A和背包集B，边(aj,bi)∈E当且仅当物品aj的大小不超过背包bi的容量，即sj≤Ci.

给定实例I的一个最优解，易知每一个背包中恰好装有2个物品ai1和ai1，且这2个物品的大小都不超过背包容量，因此对应的边 (aj1,bi),(aj2,bi)∈E. 这意味着，二部图G=(A∪B,E) 中存在一个基数为m的匹配. 给定G=(A∪B,E) 的任意一个基数为m的匹配M⊆E，对每一条边 (aj,bi)∈M，由图G=(A∪B,E) 的构造知，对应的物品aj的大小不超过Ci，因此，将每一条边 (aj,bi)∈M对应的物品放入背包bi，从而构造出实例I的一个目标函数值为1的可行解. 利用二部图的完美匹配算法[21]可以在多项式时间内求出图G的完美匹配M，因此，可以在多项式时间内找到带背包约束的基数公平分配问题的一个目标函数值至少为1的可行解. 证毕.

对一个给定的实例I=(A,B,s,C)，带背包约束的基数公平分配问题的整数规划的松弛形式[23]

利用线性规划求解算法可以得到 RLP(I)的一个最优分数解对i=1,2,···,m，令在 RLP(I) 的最优解中，可以证明至少存在一个满足 |Ai|≥k-2的背包bi.将Ai中的物品放入背包bi，并在实例I删除背包bi和Ai中的物品. 对剩余的物品和背包重新构造一个整数规划的松弛形式 RLP(I). 重复此过程，直至所有的背包中都至少装有k-2 个物品. 算法具体描述如下：

迭代取整算法

输入：n个物品构成的集合A，m个背包构成的集合B；物品aj∈A的大小为sj.

输出：m个互不相交的物品子集S1,S2,···,Sm.

第1步：若背包集非空，则求解 RLP(I),得到分数最优解

第2步：对i=1,2,···,m，置

第3步：令i*∈argmax |Ai|，B←B{bi*}，Si*=Ai*，且A←AAi* 中下标最小的k(m-1)个物品. 置I=(A′,B′,s,C)，并转第1步.i

定理9当背包的容量均相同且n≥3m 时，迭代取整算法可以在多项式时间内找到一个目标函数值至少为k-2 的可行解.

证明由基本假设知，数学规划 RLP(I)存在目标函数值为k的分数最优解对j=1,2,···,km，若存在一个背包bi满足，则称物品aj是分离的. 由于 RLP(I)的约束个数为 (k+2)m，最优解中至多有 (k+2)m个非零变量又因为每一个物品至少产生一个非零变量，且km个物品都被分配，所以最优解中至多有 2m个分离的物品. 对一个背包bi(i=1,2,···,m)，令表示装入背包bi的非分离的物品集，则有

因此存在着一个背包bi满足 |Ai|≥k-2. 由于

将Ai的物品放入背包bi，不会超过该背包的容量，且背包bi中至少装有k-2 个物品. 由算法的选择知，迭代取整算法中所选择的背包bi* 中至少装有k-2 个物品.

令A′表示AAi* 中下标最小的k(m-1)个物品，且B′=B{bi*}.对每一个背包bi∈B′，若中的所有物品的下标都不超过k(m-1)，则由的定义知

重复上述分析过程，最后可以证明迭代取整算法的输出解中，所有的背包中都至少装有k-2 个物品.证毕.

4 总结

本文研究了带背包约束的基数公平分配问题，并分别设计了背包容量相同和背包容量不同时的不可近似比与几乎最佳的近似算法. 未来可以考虑更一般情况下的带背包约束的公平分配问题，例如物品的价值不等、带指派约束等.