分数阶不确定Rössler 混沌系统的自适应滑模同步
2021-03-23毛北行王东晓
毛北行,王东晓
(郑州航空工业管理学院数学学院,河南郑州450015)
混沌系统的同步控制广受关注[1-4]。近年来,针对分数阶混沌同步问题的研究不断深入,并取得了一系列研究成果[5-9]。例如,文献[10]研究了超混沌分数阶Bao 系统的反馈同步;文献[11]研究了一类分数阶不确定Victor-Carmen 混沌系统的自适应滑模同步控制;文献[12]基于比例积分滑模方法研究了分数阶不确定超混沌Bao 系统的同步。在实际应用中,模型的不确定性、被控对象的结构变化、测量误差以及外部扰动等均会影响系统的性能,因此,须考虑这些因素造成的影响。例如,文献[13]研究了具有有界外扰和不确定项的分数阶超混沌金融系统滑模同步的4种方法。Rössler 混沌系统的同步亦广受关注。例如,文献[14]研究了基于back-stepping 方法对超混沌Rössler 系统的控制与同步;文献[15]研究了双时滞Rössler 系统的分支分析与混沌控制;文献[16]研究了基于曲率指数的耦合混沌系统的完全同步分析。受上述结论启发,笔者利用自适应滑模控制方法,研究了带有模型不确定性和外扰的Rössler混沌系统的同步问题,得到分数阶不确定Rössler 混沌系统取得适应滑模同步的充分条件,所得结论说明不确定Rössler 混沌系统在一定条件下取得了自适应滑模同步。最后,用数值仿真实验对结论进行了检验。
1 主要结果
定义1[17]Caputo 分数阶导数定义为

以分数阶Rössle 混沌系统
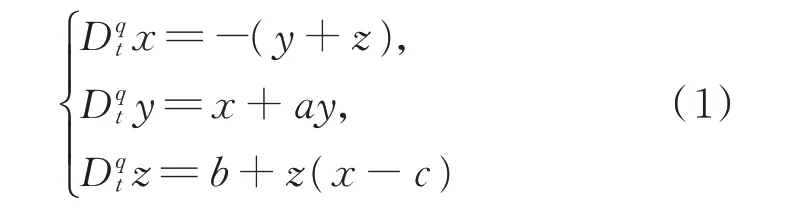
为主系统,当a=0.2,b=0.2,c=5.0,q=0.92 时,系统的时域波形图和相平面图分别如图1 和图2 所示。
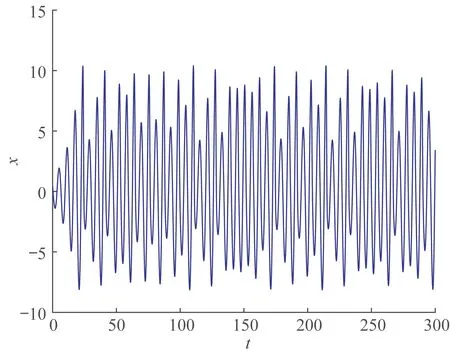
图1 系统的时域波形图Fig.1 Time domain of the system
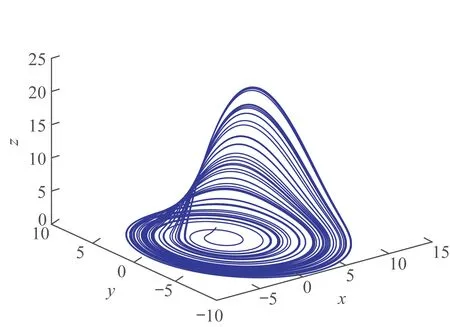
图2 系统的相平面图Fig.2 Phase plane of the system
从系统为
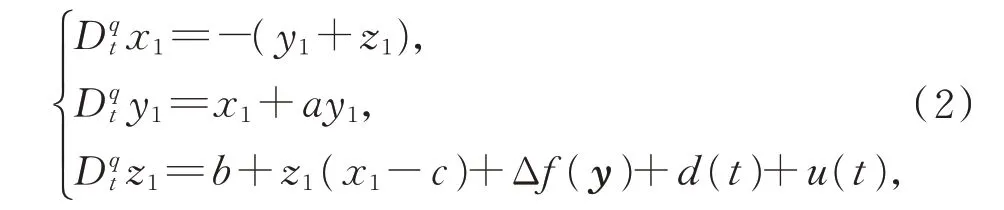
其中,不确定项Δf(y),y=[x1,y1,z1]T,d(t)为外扰,u(t)为控制器。定义
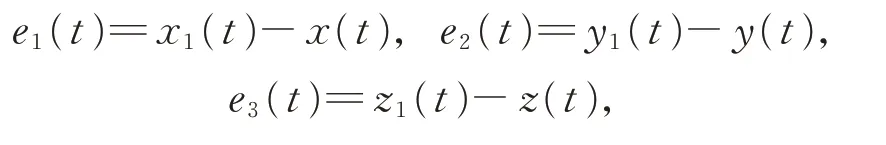
得到误差方程:
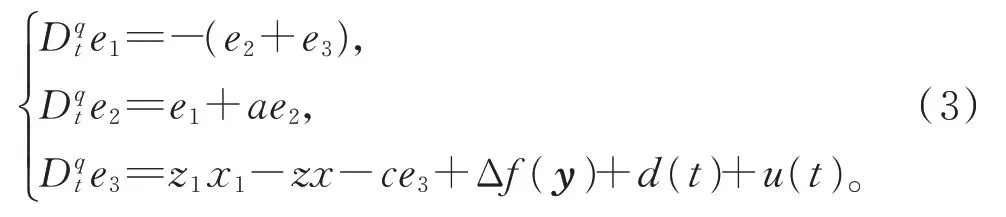
假设1假设不确定项Δf(y)和外部扰动d(t)有界,即存在未知参数m,n>0,使得
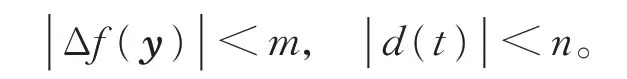
引理1[18]若x(t)为连续可微函数,则有
引理2[18]设其中,y1(t),y2(t)∈R 具有连续一阶导数,若存在常数k>0,使 得有界,且其中,Eα,1(·)表 示 双 参 数Mittag-Leffler 函 数,则y1(t)具Mittag-Leffler 稳定且
定理1在假设1 条件下,设计滑模面s=设计控制器
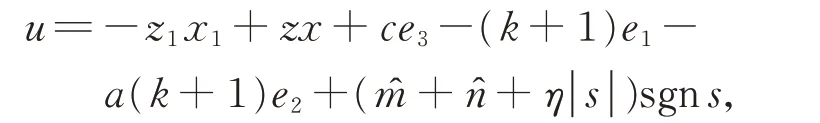
其中,ˆ分别为m,n的估计值,η>0。则式(1)和式(2)适应滑模同步。
证明滑模面上由式(3)第1 个方程,得−(e2+e3)=ke2。
进一步得到e3=−(k+1)e2,对式(3)第2 个方程两边同求q阶微分,得到因 为所 以利 用 Laplace 变 换 ,记E2(s)=L(e2(t)),则有
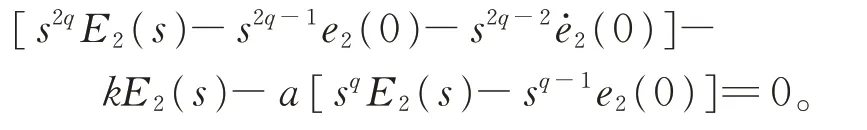
由Laplace 终值定理,有
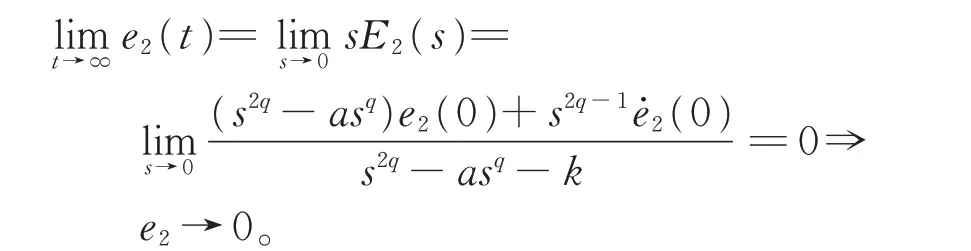
由 于e3=−(k+1)e2⇒e3→0,且e2→0 ⇒,将 其 代 入 式(3)第2 个 方 程,有=e1+ae2⇒e1→0。
所以,定义的滑模面具有稳定性。
下证滑模面的可达性。

由引理2,有s→0。
以整数阶Rössle 混沌系统
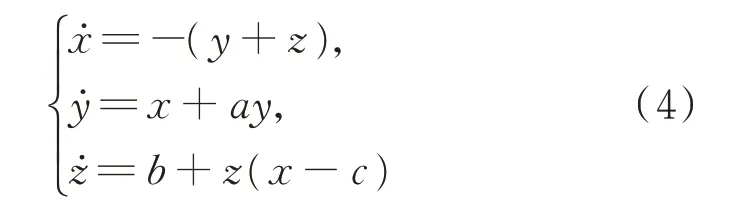
为主系统,从系统为

定义
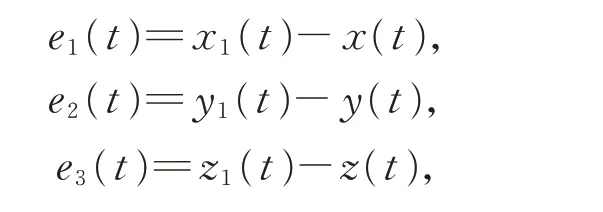
得误差方程
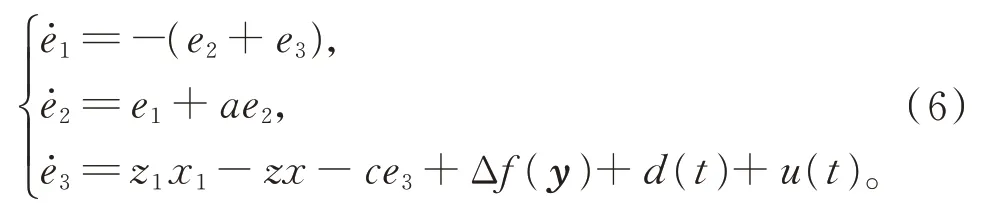
引 理3(Barbalat’s)[19]若 函 数f(t) 在[0,+∞)上一致连续,且广义积分存在,则其中,f(t)为一致连续函数。
定理2在假设1 条件下,设计滑模面s=设计控制器
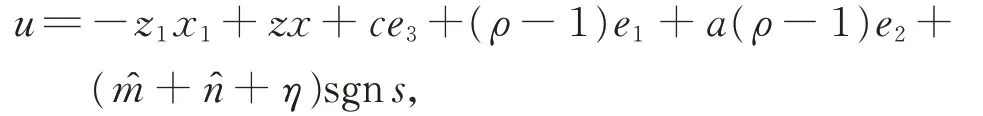
其中,ˆ分别为m,n的估计值,η>0。则式(4)和式(5)适应滑模同步。
证 明滑 模 面 上即−(e2+e3)=−ρe2,进一步得到e3=(ρ−1)e2,对式(6)第2 个 方 程 求 一 阶 微 分,得 到因为所 以以e2(t)为变量,则其特征值由于ρ<0,所以又由于混沌系统轨迹有界,所以|e2(t)|必有界,从而必 有C1=0。 否 则,若C1≠0 ⇒e2无 界,易 得由 于e3=(ρ−1)e2⇒e3→0, 将代入式(6)第2 个方程,得到e1→0。
所以,定义的滑模面具有稳定性。
下证滑模面的可达性。
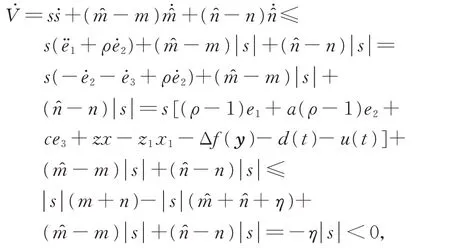
证毕!
2 数值仿真
以MATLAB 仿真程序对上述系统进行数值仿真,选取初始值及系统参数为
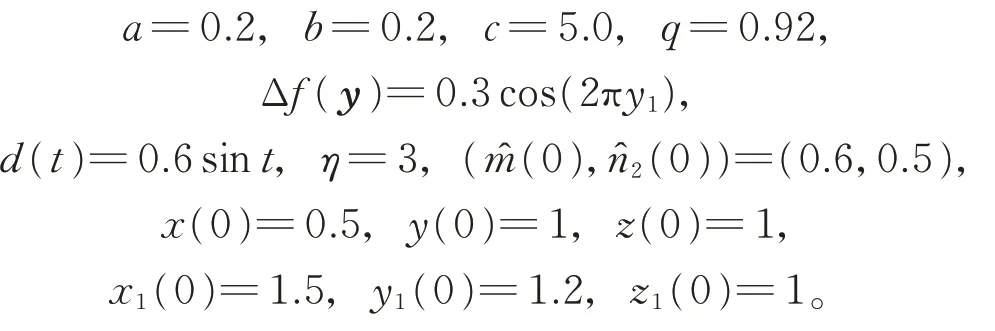
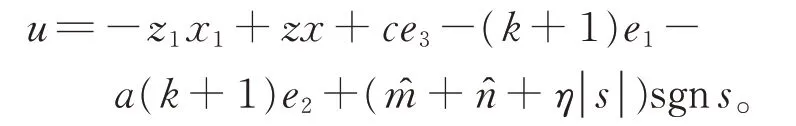
在定理2 中,设计滑模面
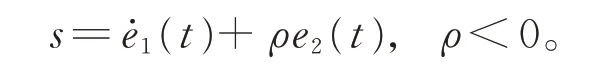
在定理1 中,设计适应律
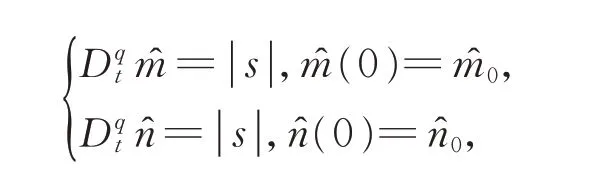
在定理2 中,设计控制器
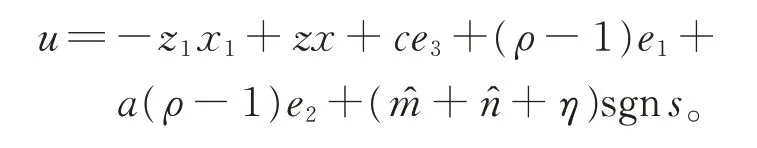
在定理2 中,设计适应律
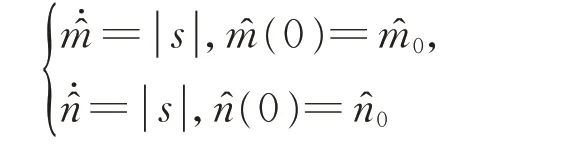
定理1 和定理2 的误差分别如图3 和图4 所示,由图3 和图4 知,初始时刻误差相差较大,距离原点较远,随着时间的推移,误差逐渐趋于一致,趋向坐标原点,表明系统取得了滑模同步。
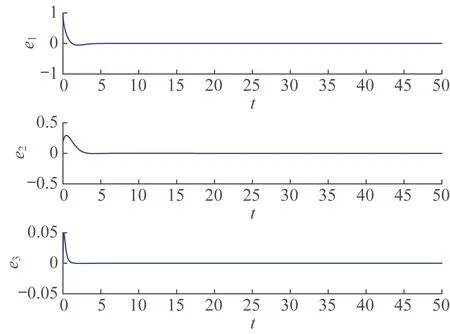
图3 定理1 的误差Fig.3 Errors in theorem 1
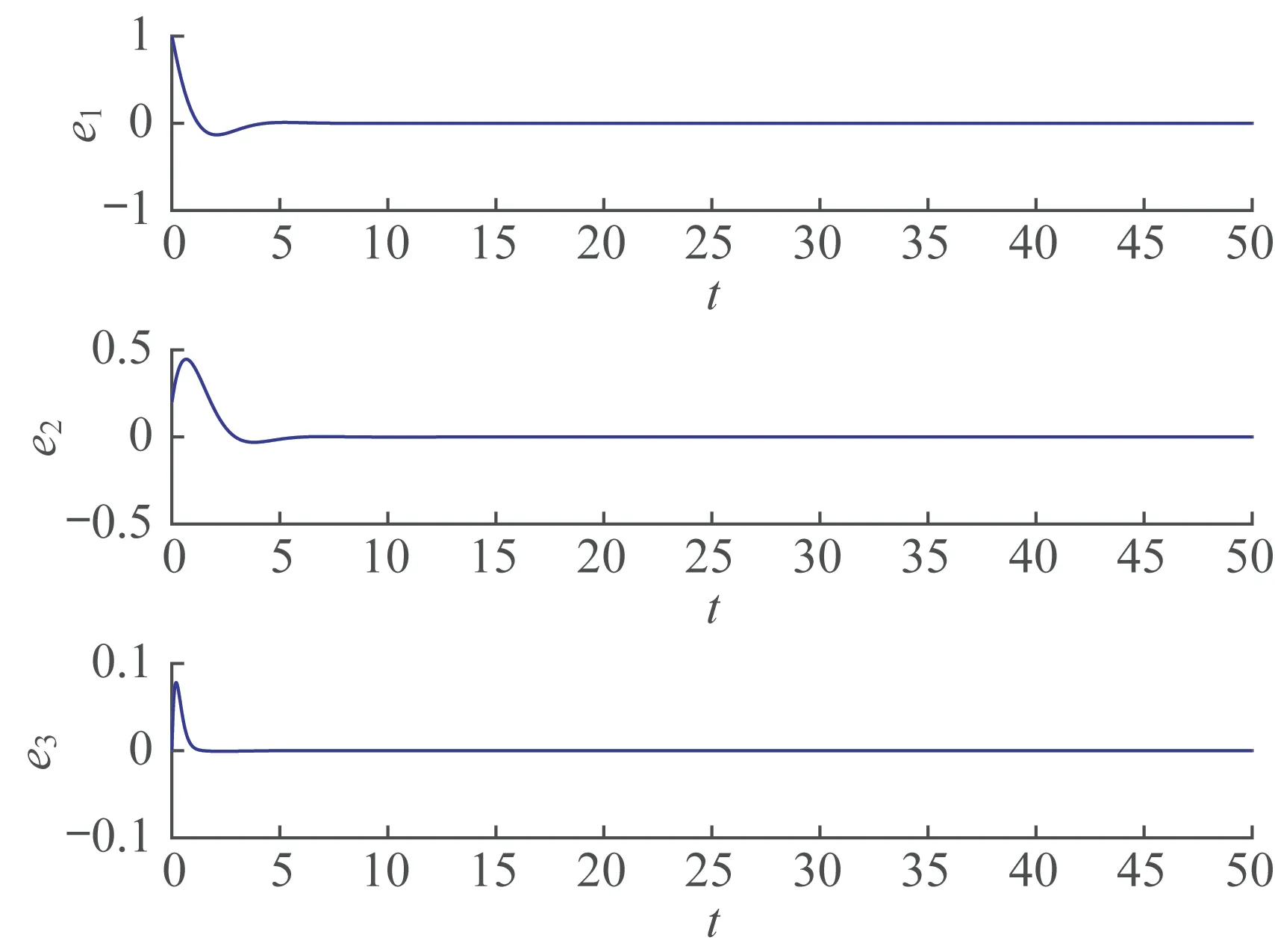
图4 定理2 的误差Fig4 Errors in theorem 2
3 结 论
研究了具有模型不确定性和有界外部扰动的分数阶不确定Rössler 混沌系统的自适应滑模同步问题。通过构造适当的滑模面、控制器和适应律,得到分数阶不确定Rössler 混沌系统的自适应滑模同步的充分条件。本文方法不仅适用于分数阶混沌系统,而且可平推至整数阶系统。
