无额外自由度广义有限元非线性分析
2021-03-19马今伟段庆林陈嵩涛
马今伟,段庆林,陈嵩涛
(大连理工大学 工业装备结构分析国家重点实验室,大连 116024)
1 引 言
广义有限元法[1]能够方便地引入待求解问题相关的局部强化函数,具有计算精度高、易于程序实现(对已有的有限元程序改动较小)等优点,引发了广泛关注。该方法一般认为源于单位分解法[2]和单位分解有限元法[3],甚至还可追溯到更早期的研究[4,5]。由于局部强化函数可以根据具体问题方便灵活地引入,广义有限元法已广泛应用于各类问题,如裂纹扩展[6]、形状优化[7]、非光滑界面[8]和水力压裂[9]等。
在广义有限元法[1]中,局部强化函数的引入依赖于额外自由度。以本文考虑的静力问题为例,每个计算节点除标准的位移自由度之外,还需设置与局部强化函数数目相等的额外自由度。这导致了求解规模的急剧增大。更为严重的是,依赖额外自由度引入局部强化函数会造成线性相关性问题[3,10,11],导致刚度阵奇异。针对该问题,目前已有一些行之有效的方法,如稳定广义有限元方法(SGFEM)[12]以及正交广义有限元方法(OGFEM)[13]等。这些方法能有效消除线性相关性问题,但仍然需要使用额外自由度,不能减小求解规模,实现起来也与标准有限元法有较大差异。
田荣[14]采取了一种不同的思路,提出不使用额外自由度引入局部强化函数,建立了无额外自由度广义有限元法。该方法不仅消除了前述线性相关问题,而且节点自由度与标准有限元法相同,同时仍然保留了广义有限元方法的诸多优势,如局部强化函数仍然能够方便灵活地引入。基于这一思想,田荣等[15,16]也对广泛应用于裂纹问题的扩展有限元法进行了改进,建立了iXFEM(improved XFEM)方法。同样地,无额外自由度广义有限元法作为对原GFEM方法的重要改进,在本文中简记为iGFEM。
目前,对于本文考虑的静力问题,iGFEM仍然仅限于线弹性小变形分析。本文将基于考虑几何和物理非线性的计算方法理论[17-20],将该方法推广至弹塑性大变形问题的非线性分析。虽然,有限元法的非线性分析相对成熟,并已发展了诸多计算软件,包括我国自主软件SiPESC[21]。但是,低阶单元非线性分析的计算精度往往难以令人满意。iGFEM 方法可使用低阶单元的计算网格建立高阶的插值近似,若能有效改善非线性分析的计算精度,将具有重要的研究意义和潜在的应用价值。
2 控制方程
参考初始构型,静力平衡方程及边界条件为
∂Pi j/∂Xj+bi=0inΩ0
(1)
(2)

Wext-Wint=0
(3)
式中Wint和Wext分别表示内力和外力虚功:
(4)
(5)
式中δui为虚位移。弱形式(3)的进一步空间离散依赖于位移场的插值近似,这是iGFEM方法的核心内容。
3 无额外自由度的广义有限元近似
广义有限元方法的位移近似可写为
(6)

(7)
该式可进一步写为
(8)
式中
(9)


图1 计算网格上的节点片
(10)
其中
(11)
式中ω(x)为MLS的权函数,pK=p(xK),本文取为如下的二次基底
(12)
4 节点力及其线性化
为得到离散化方程,将iGFEM的位移近似式(8)代入弱形式(3),并通过位移的独立变分可得到
(13)
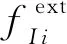

(14)
(15)
式(13)是以位移为基本未知量的非线性方程,需采用Newton-Raphson迭代求解。为此,对节点内力作如下线性化
(16)
式(16)的推导利用了以下关系:
(17)

(18)
其中
(19)
(20)
应说明的是,本文仅考虑不随构形变化的外载,因而无须对节点外力进行线性化。
5 本构模型
本文考虑的亚弹-塑性材料的弹性本构关系可写为
(21)

(22)
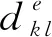
(23)

(24)
式中γ为塑性参数,rk l为塑性流动方向。对于本文考虑的J2关联塑性有rk l=∂f/∂σk l,f为屈服面。
(25)
式中q为内变量,在本文仅考虑为等效塑性应变,‖ξ‖为等效应力,K(α)=σY+Hα为后继屈服强度,σY为初始屈服强度,α为等效塑性应变,H为塑性模量。将式(23,24)代入式(21)可得
(26)

(γ≥0,f≤0)(27)
对于本文考虑的超弹性材料,本构模型可由第二PK应力Si j和格林应变Ek l写为
(28)

(29)
将上述两种本构模型代入式(18),则节点内力率可写为
(30)

(31)
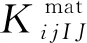
(32)

6 数值算例
采用三个算例考察本文发展的非线性iGFEM 方法处理弹塑性大变形问题的有效性和计算精度。为作比较,对标准线性有限元方法也进行了数值实现,并标记为FEM。
6.1 浅拱
如图2所示,两端固支弧形浅拱在顶部中心点A处受向下的集中力作用。浅拱中性轴半径为100 mm,拱厚为2 mm,浅拱对应圆心角为28.06°,材料为超弹性,杨氏模量E=4.8×103N/mm2,泊松比υ=0。iGFEM方法计算得到的浅拱变形及相应的σx x应力场如图3所示。图4比较了两种方法的载荷-位移曲线。在相同的计算网格下,iGFEM 的计算结果与解析解吻合,FEM则发生了明显的偏离。应说明的是,本文FEM仅指标准的线性三角形单元,若采用高阶单元或使用精巧的单元技术,有限元法的计算精度将会得到显著提高。
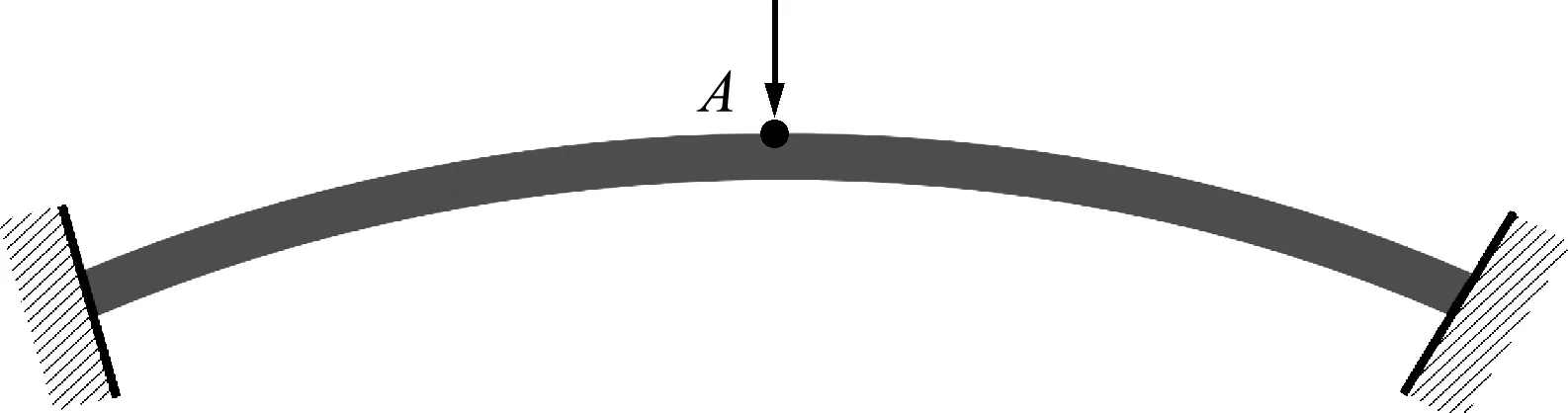
图2 受集中力作用的浅拱

图3 浅拱变形及σxx应力场

图4 浅拱A点处的载荷-位移曲线
6.2 悬臂梁
如图5所示,悬臂梁一端固支,另一端受向上大小为F=10 N的集中力作用,梁长为20 mm,厚度为1 mm,材料为超弹性,杨氏模量E=4.8×103N/mm2,泊松比υ=0。iGFEM计算得到的悬臂梁变形过程如图6所示。图7比较了悬臂梁自由端的载荷-挠度曲线,再次展现了iGFEM方法的高精度。
6.3 圆杆颈缩
采用圆杆颈缩问题考察本文方法对于亚弹-塑性材料大变形计算的有效性。如图8所示,圆杆长为53.334 mm,半径为6.413 mm,两端各施加 7 mm 的固定位移。由于对称性,只取圆杆的1/4

图5 自由端受集中力的悬臂梁

图6 悬臂梁变形过程

图7 悬臂梁载荷-挠度响应对比
进行数值模拟。在圆杆中间截面处引入几何缺陷,该处的半径为两端半径的98.2%。具体的材料参数和实验数据可以参考文献[22]。
采用图9所示的两种计算网格,FEM和iGFEM 计算得到的颈缩曲线与实验数据[22]在 图10 进行了比较。两种方法计算得到的圆杆颈缩变形分别如图11和图12所示。可以看出,FEM粗细两种网格的计算结果有明显差异,而iGFEM粗细网格的计算结果基本保持一致,这在一定程度上验证了iGFEM方法在粗网格下具有良好的高精度特性。
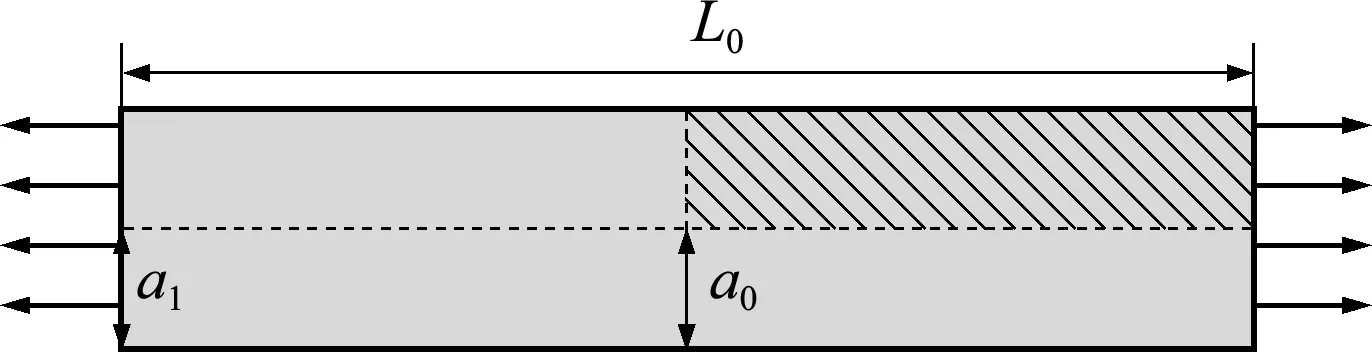
图8 圆杆颈缩算例

图9 圆杆颈缩算例的计算网格

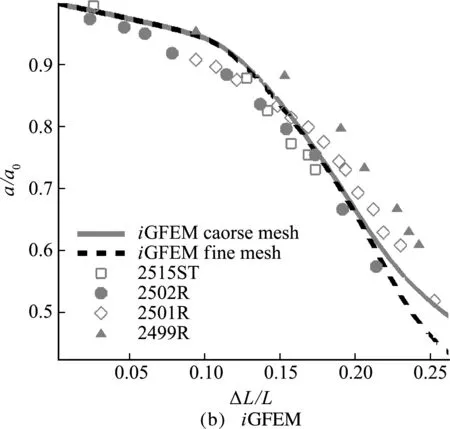
图10 圆杆颈缩算例的颈缩-位移曲线

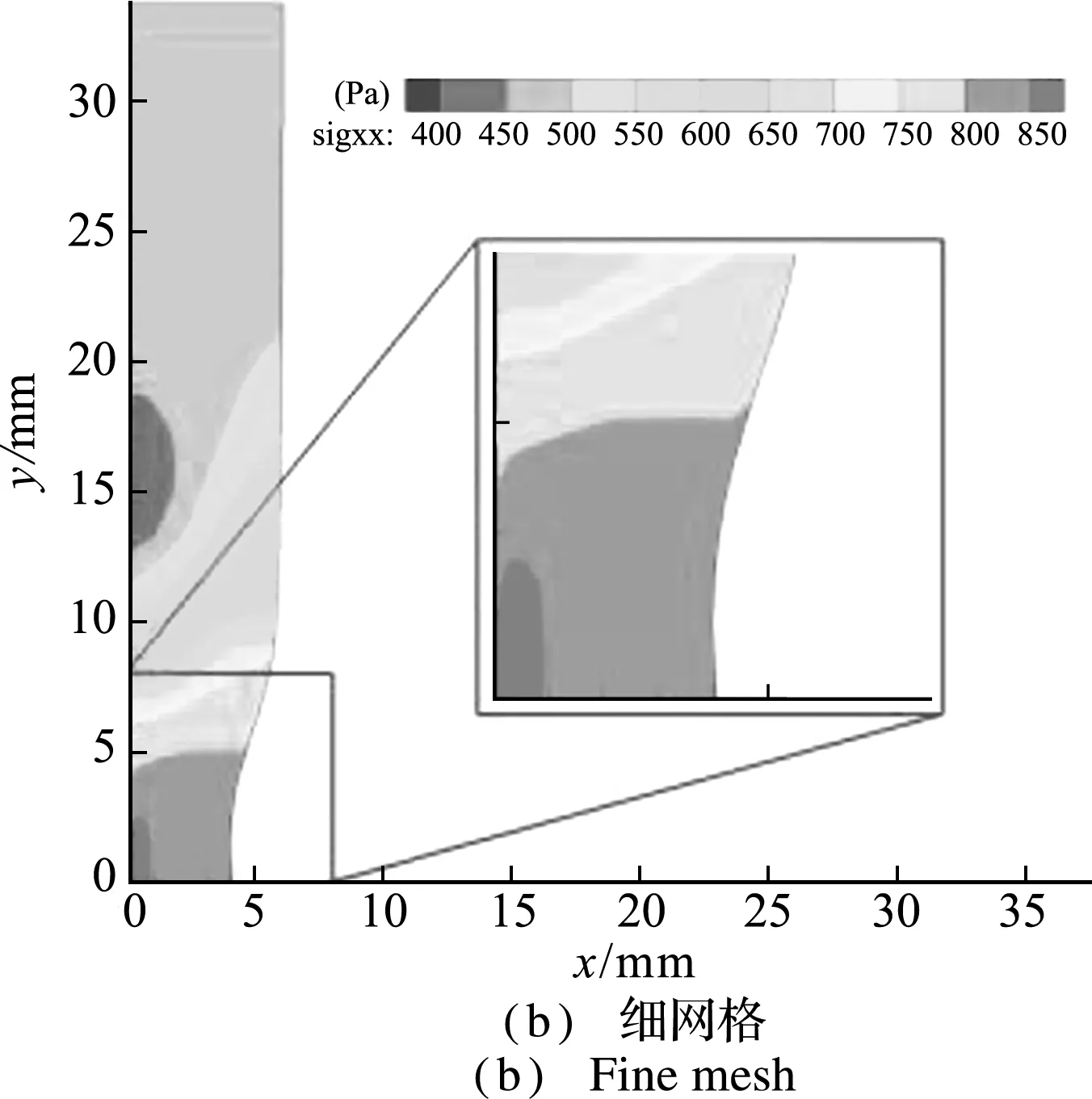
图11 FEM方法得到的圆杆颈缩变形


图12 i GFEM方法得到的圆杆颈缩变形
7 结论与展望
本文建立了几何和物理非线性分析的无额外自由度广义有限元方法。数值结果表明,本文方法不仅能有效分析弹塑性大变形问题,而且展现出优于传统线性有限元方法的计算精度。后续工作将把该方法推广至三维,面向复杂工程问题,有力推动弹塑性大变形高精度计算方法的发展。
