Li Wang(王利), Qing Liu(刘青), and Yunbo Zhang(张云波)

1Institute of Theoretical Physics,State Key Laboratory of Quantum Optics and Quantum Optics Devices,

Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China

2Key Laboratory of Optical Field Manipulation of Zhejiang Province and Physics Department of Zhejiang Sci-Tech University,Hangzhou 310018,China

Keywords: quantum walk,non-Hermitian lattice,dissipations,edge states

1. Introduction

Quantum walk,[1,2]originated as a quantum generalization of classical random walk, has now become a versatile quantum-simulation scheme which has been experimentally implemented in many physical settings,[3]such as optical resonators,[4]cold atoms,[5,6]superconducting qubits,[7–9]single photons,[10,11]trapped ions,[12]coupled waveguide arrays,[13]and nuclear magnetic resonance.[14]For standard Hermitian systems,quantum walk has been proposed to detect topological phases.[15–17]And those fundamental effects of quantum statistics,[18,19]interactions,[19–24]disorders,[25–27]defects,[28,29]and hopping modulations[23,29–32]on the dynamics of quantum walkers have also been intensively investigated.

Recently, non-Hermitian physics[33–61]has been attracting more and more research attention, since gain and loss are usually natural and unavoidable in many real systems,such as coupled quantum dots,[62]optical waveguides,[63]optical lattices,[64–67]and exciton–polariton condensates.[68,69]In this context, the central concept of bulk–boundary correspondence which was developed for Hermitian systems is carefully examined and reconsidered in many concrete non-Hermitian models.[37,70–77]Anomalous zero-energy edge state is found in a non-Hermitian lattice which is described by a defective Hamiltonian.[78]The concept of generalized Brillouin zone (GBZ) is proposed and a non-Bloch band theory for non-Hermitian systems is established for one-dimensional tight-binding models.[79–86]With the aid of non-Bloch winding number, the bulk–boundary correspondence for non-Hermitian systems is restored. Concurrently, the study on quantum walk has also been extended to non-Hermitian systems.Quantum dynamics of non-Hermitian system is believed to be quite different from that of standard Hermitian case.And topological transitions in the bulk have already been observed for open systems by implementing non-unitary quantum walk experimentally.[63,87–89]

In this work,we consider a non-Hermitian quantum walk on a finite bipartite lattice in which there exists equal loss on each site of one sublattice. Whenever the quantum walker resides on one of the lossy sites, it will leak out at a rate that is determined by the imaginary part of the on-site potential.As time elapses,the quantum walker initially localized on one of the non-decaying sites will completely disappear from the bipartite lattice eventually. Given the ability to record the position from where decay occurs,one may routinely obtain the resultant decay probability distribution. Intuitively, one may expect the decay probability on each unit cell decreases as its distance from the starting point of the quantum walker increases since each unit cell has a leaky site with equal decay strength. Surprisingly, our numerical simulation displays a very counterintuitive distribution of the decay probability in one parametric region, while the intuitive picture described above shows in the rest region. A conspicuous population of decay probability appears on the edge unit cell which is the farthest from the initial position of the quantum walker,while there exists a lattice region with quite low population between the edge unit cell and the starting point.We analyze the energy spectrum of the finite bipartite non-Hermitian lattice with open boundary condition. It is shown that the exotic distribution of decay probability is closely related to the existence and specific property of the edge states, which can be well predicted by the non-Bloch winding number.[79,80]

The paper is organized as follows. In Section 2,we introduce the bipartite non-Hermitian model with pure loss. And detailed description of the quantum walk scheme is also addressed. In Section 3,concrete numerical simulations are implemented for a finite non-Hermitian lattice with open boundary condition. Corresponding distributions of the local decay probability obtained numerically are shown for several typical choices of the model parameters. We then compute the band structure of the finite bipartite lattice with open boundary condition in Section 4. Portraits of the intriguing edge states are pictured therein. And with a constant potential shift, our model is transformed into a model possessing balanced gain and loss. Accordingly, both the Bloch and non-Bloch topological invariants which are vital to bulk–boundary correspondence are calculated. Finally, a summary along with a brief discussion is given in Section 5.

2. Model and method

We investigate continuous-time quantum walks on a finite one-dimensional bipartite lattice of length L with pure loss,which is pictured in Fig.1. This tight-binding model can be well described by a non-Hermitian Hamiltonian H, which reads

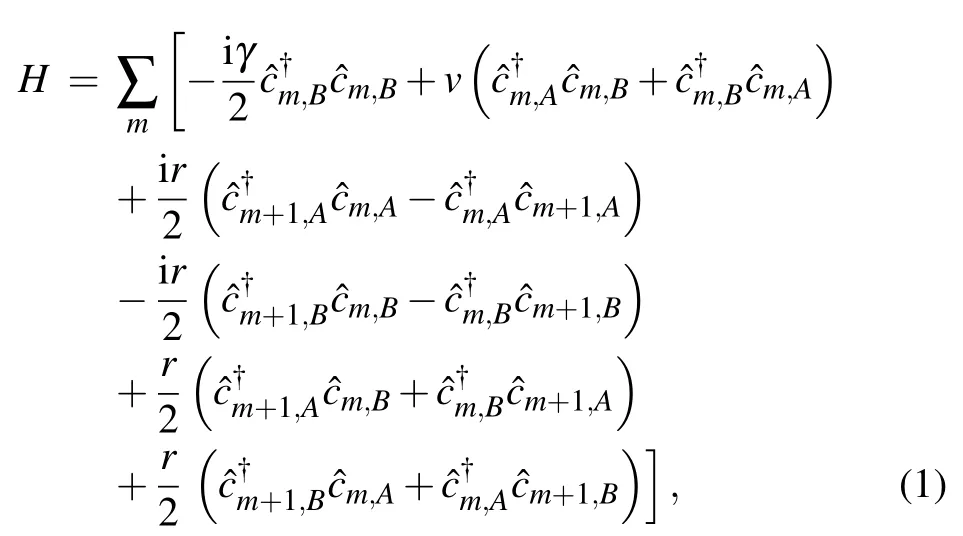
Fig.1. Schematic figure of the tight-binding non-Hermitian lattice. Each unit cell contains two sites,A and B. Decay with rate γ occurs on each site of the sublattice B. The arrow denotes the phase direction.

Accordingly, the dynamics of a quantum walker in state|ψ〉 dwelling on such a bipartite lattice with long-range hopping obeys the following equations of motion:

Suppose the quantum walker is initially prepared on the A site of unit cell o at time t =0,then the initial state|ψ(0)〉of the quantum walker is given by following amplitudes:

For time t >0, the quantum walker will move freely on the bipartite lattice according to the equations of motion(2). Due to the existence of pure loss in Hamiltonian(1),whenever the quantum walker visits the sites of sublattice B,it will leak out with a rate γ according to Eq. (3). As t →∞, the probability of the quantum walker dwelling on the lattice decreases to be zero. Given the ability to detect the position of the site from where the probability of the quantum walker leaks out,one can obtain the local decay probability Pmon each leaky unit cell m.According to Eq.(3),we have

3. Distribution of the local decay probability Pm

We investigate dissipative quantum walks on a finite lattice with L unit cells and under open boundary condition.Without loss of generality, the size of the lattice is taken to be L=51. The quantum walker is set out from the non-leaky site of unit cell o in the bulk. As mentioned in Section 2, the bipartite lattice sketched in Fig.1 is a system with pure loss on each B site, one may immediately has an intuitive picture in mind that the local decay probability Pmshrinks quickly as the distance of the unit cell m from the starting point of the quantum walker increases since the decay strength on each B site is equal. The underlying reason for this is obvious. First come,first served. The quantum walker visits the nearby unit cells first, then more probability leaks out there. Because, as time elapses, the remaining part of the norm of the quantum walker state |ψ(t)〉 becomes smaller and smaller. However,direct numerical simulations present intriguing distributions of the local decay probability Pm.The picture turns out to be quite counterintuitive where a relatively high population of the local decay probability on the edge unit cell occurs in the resultant distribution. This is very surprising since the edge unit cell is the farthest from the initial position of the quantum walker.

In Fig.2, we simulate the non-Hermitian quantum walk for positive intracell hopping v by numerically solving the equations of motion (2). The resultant distributions of local decay probability Pmamong the whole lattice are shown for the intracell hopping v taking values 0.3,0.5,0.7,0.9.And the decay strength is set to be γ=1,the intercell hopping strength to be r=0.5. Correspondingly,time evolutions of the probability distributions|ψAm(t)|2+|ψBm(t)|2for all lattice unit cells are shown in the insets. As shown in Fig.2, the distributions of the local decay probability are all asymmetric. The quantum walker initiated from the center unit cell o tends to move to the left of the bipartite lattice for positive intracell hopping.And more surprising is that for v=0.3 and v=0.5 as shown in Figs.2(a)and 2(b),an impressive portion of the probability decays from the left edge unit cell which is the farthest one from the unit cell o. Besides, the intuitive picture previously mentioned also shows up, which is shown in Figs. 2(c) and 2(d)for the intracell hopping v=0.7 and v=0.9. As the distance of the unit cell m from the center unit cell o increases,the portion of the probability that leaks out from m becomes smaller and smaller.

We then simulate the non-Hermitian quantum walk for negative intracell hopping v with other parameters the same as the positive case above. Details of the distributions of local decay probability Pmare shown in Fig.3 and density plots of the probability distributions among the whole lattice during the quantum walk processes are shown in insets. Similar to the case of positive v, the resultant distributions are also asymmetric. However, in this case the quantum walker has a tendency to go to the opposite direction. Namely, most of the probability of the quantum walker flows to the right side of the bipartite lattice and leaks out there subsequently. Also,as shown in Figs. 3(a) and 3(b), a conspicuous population of the decay probability appears on the rightmost unit cell for intracell hopping v=−0.3 and v=−0.5. And as the strength of the intracell hopping increases,for the cases v=−0.7 and v=−0.9 as shown in Figs.3(c)and 3(d),the expected distribution of local decay probability Pmis restored again.

Fig.2. Resultant distributions of the local decay probability Pm obtained at the end of the non-Hermitian quantum walks on a finite bipartite lattice.Insets show the corresponding quantum walk processes.The intracell hopping v takes positive values,with(a)v=0.3,(b)v=0.5,(c)v=0.7,(d)v=0.9. The lattice consists of L=51 unit cells with r=0.5 and the decay strength γ =1.

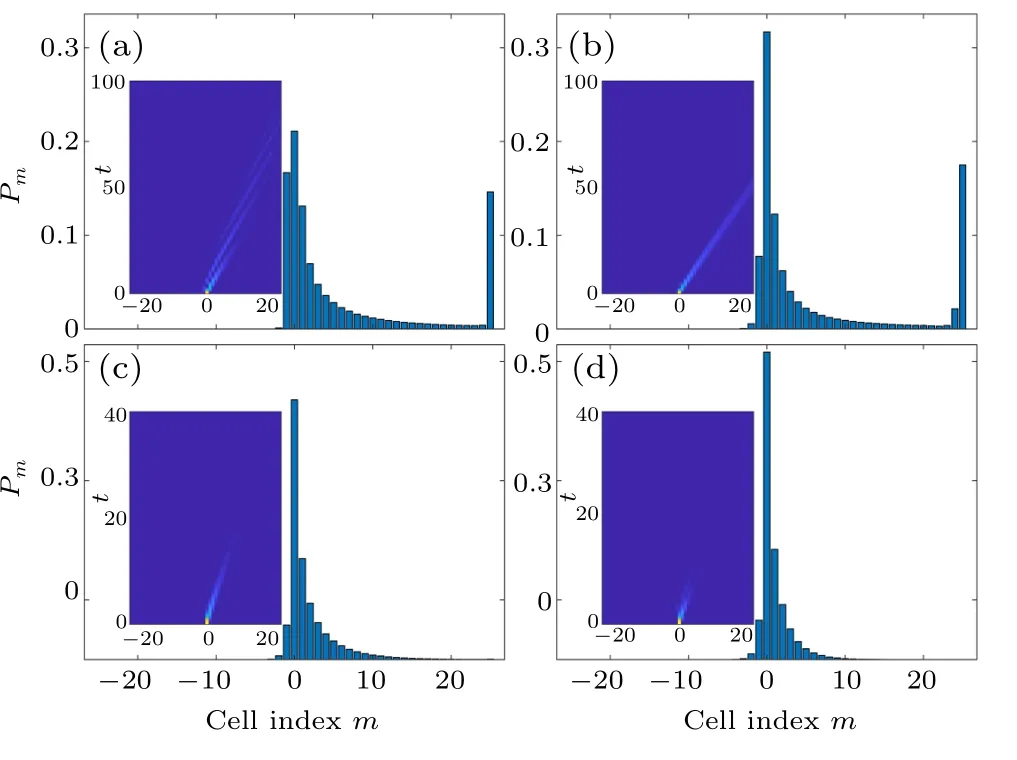
Fig.3. Resultant distributions of the local decay probability Pm obtained at the end of non-Hermitian quantum walks on a finite bipartite lattice with L=51 unit cells for negative intracell hoppings v. Corresponding quantum walk processes are shown in insets. (a)v=−0.3,(b)v=−0.5,(c)v=−0.7,(d)v=−0.9. The decay strength γ =1 and r=0.5.

Finally, numerical simulation of a quantum walk on the lossy non-Hermitian lattice with intracell hopping v = 0 is shown in Fig.4(a). Since the intracell hopping is zero, there is no direct particle exchange between the two sites within the same unit cell. The quantum walker set out from the central unit cell o will preferentially go to lattice sites of nearby two unit cells o −1 and o+1 rather than the lossy site B of unit cell o. Therefore,little probability leaks out from the starting point of the quantum walker. Indeed,this is the case revealed by the resultant decay probability distribution, see Fig.4(b).In contrast to the counterintuitive cases with finite strength of intracell hopping as shown in Figs. 2 and 3, the distribution of local decay probability Pmis nearly symmetric among the whole lattice.

Fig.4. (a) The non-Hermitian quantum walk on a finite bipartite lattice with L=51 unit cells for intracell hopping v=0, decay strength γ =1,and r=0.5. (b)Symmetric distribution of local decay probability Pm obtained at the end of the non-Hermitian quantum walk.

Interestingly, the quantum walk dynamics demonstrated by the numerical simulations above seems quite like a quantum switch. And apparently,by modulating the strength of the intracell hopping v,the quantum walker could be regulated at will to reach the left edge unit cell, the right edge unit cell,or none of them with an impressive portion of the probability. This mechanism may have potential applications in the designing of micro-architectures for quantum information and quantum computing in future.

4. Energy spectrum of the lossy bipartite lattice

To gain a deep insight into the exotic dynamics shown above,in this section we turn to analyze the band structure of the finite bipartite non-Hermitian lattice with open boundary condition in real space. Varying the strength of intracell hopping v,the corresponding Hamiltonian matrices of Eq.(1)are numerically diagonalized and the energy spectrum is obtained.

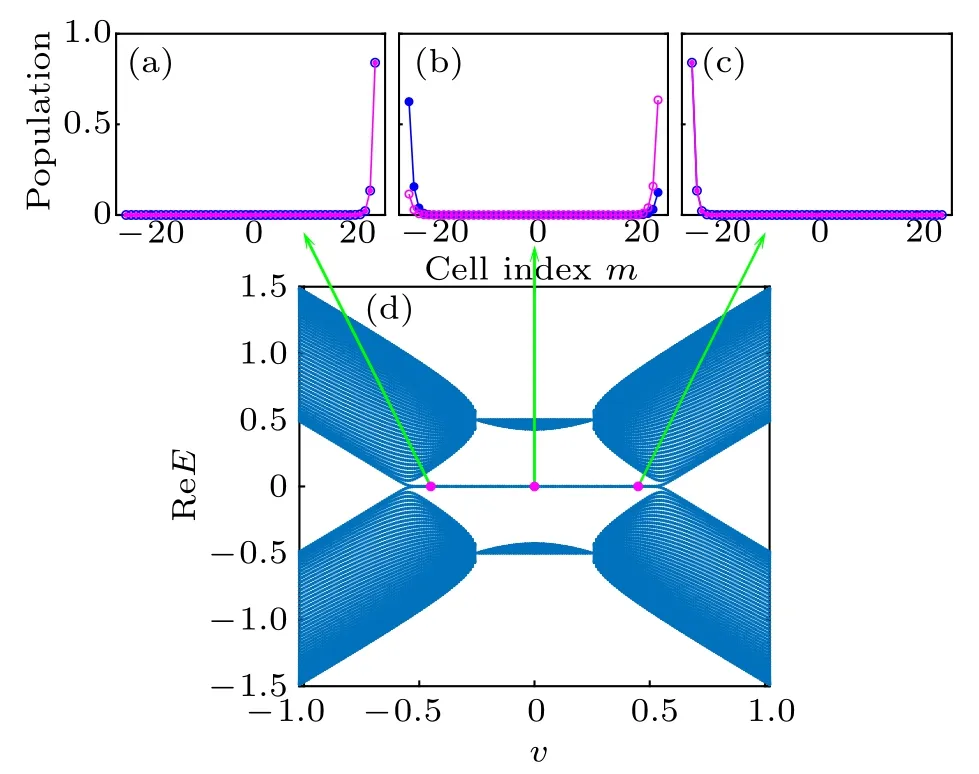
Fig.5. Energy spectrum versus intracell hopping v of the finite bipartite non-Hermitian lattice with pure loss under open boundary condition. The lattice size is L=51(unit cell)with the decay rate γ =1 and intercell hopping r=0.5. (a)–(c)Three typical profiles of edge states. (d)Real part of the single-particle energy spectrum versus intracell hopping v.

Correspondingly, the imaginary part of the openboundary energy spectrum is shown in Fig.6(a). It is shown that the imaginary parts of the eigenenergies are all located in the lower half plane. This manifests that the eigenstates are going to decay with time. And we plot|E|as a function of the intracell hopping v in Fig.6(b)where a length of straight line which is well separated from the spectrum bulk of|E|is also shown. These eigenenergies correspond to the edge states.

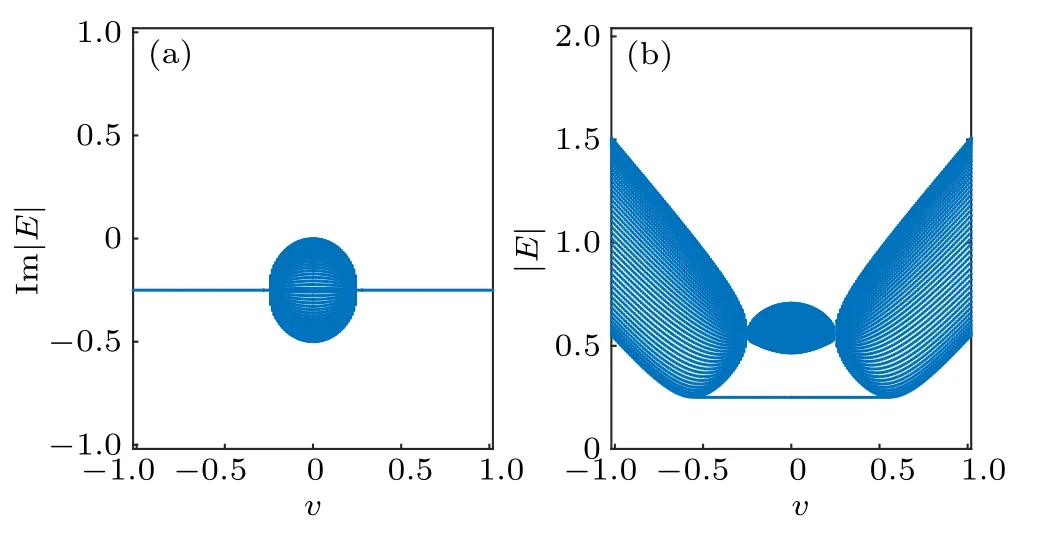
Fig.6. Energy spectrum versus intracell hopping v of the finite bipartite non-Hermitian lattice with pure loss under open boundary condition. The lattice size is L=51(unit cell)with the decay rate γ=1 and intercell hopping r=0.5. (a)Imaginary part of single-particle energy spectrum versus intracell hopping v. (b)|E|as a function of the intracell hopping v.

To investigate the topological properties of the model equation(1),it is beneficial to pass to the momentum space by Fourier transformation.Straightforwardly,the Bloch Hamiltonian is

Based on this Bloch Hamiltonian, winding numbers[92]under different values of v are calculated which are denoted by black dots in Fig.7. Unfortunately,the topologically nontrivial region revealed in Fig.7 does not match well the region in Figs. 5 and 6 where edge states emerge. And as shown in Fig.7,the winding number has a fractional value of 1/2 in the two regions.

Fig.7. Numerical results of both Bloch(denoted by black dots)and non-Bloch(denoted by magenta circles)topological invariant W as a function of the intracell hopping v.The decay rate is γ=1 and the intercell hopping strength is r=0.5.

For the case with r=0.5 and decay strength γ=1,we numerically calculate the non-Bloch winding number W as a function of the intracell hopping v.As shown in Fig.7,it is clear that for v ∈[−0.559,0.559] the system is topological nontrivial with the non-Bloch winding number W =1. Comparing Fig.5(d)and Fig.7 carefully, one can find that the edge modes in the single-particle energy spectrum could be well predicted by the non-Bloch topological invariant W.

Fig.8. Decay probability imbalance Pimb between the two edge unit cells as a function of the intracell hopping v. Region with the non-Bloch winding number W =1 is indicated by green-colored background. The lattice size is L=51 (unit cell) with the decay rate γ =1 and intercell hopping r=0.5.

Finally,we implement numerically the quantum walk on a finite bipartite non-Hermitian lattice with L=51 unit cells repeatedly with the intracell hopping v scanning through the parametric region [−1,1]. The decay rate is set to be γ =1 and the intercell hopping is fixed at r=0.5. Based on various distributions of decay probability Pmobtained during the numerical simulation above,we plot in Fig.8 the decay probability imbalance Pimbbetween the two edge unit cells as a function of the intracell hopping v. Specifically, Pimbis defined as

with l and r being the indices of the leftmost unit cell and the rightmost unit cell,respectively. For convenience of comparison,different parametric regions with different non-Bloch winding numbers are indicated by different colors. Clearly as shown in Fig.8, appearance of the counterintuitive distributions of local decay probability Pmis intimately related to the topological nontrivial region with non-Bloch winding number W =1 except for tiny mismatches at edges of the region. We infer that these tiny mismatches emerge as a result of finitesize effects since our study is concentrated on finite lattices.However,what we want to emphasize here is that the topological nontrivial region can be taken as a guide to tell us where it is possible to observe the intriguing distributions of local decay probability. When the edge modes are located at the left edge unit cell (see Fig.5(c)), conspicuous occupation of the local decay probability on the leftmost unit cell occurs. Similarly,when the edge modes are located on the right edge unit cell (see Fig.5(a)), impressive portion of the probability decays from the rightmost unit cell. Interestingly, it seems that the edge state has an attractive effect to the quantum walker walking on the non-Hermitian lattice. This is quite different from the case of Hermitian case,[32]in which the edge state exhibits repulsive behavior to the quantum walker initiated in the bulk. When it comes to the case of zero intracell hopping,each of the two edge states is localized on one of the two edge unit cells,see Fig.5(b). The attractive effects of the two edge states seem to balance in power.Therefore,an almost symmetric distribution of the local decay probability comes into force,see Fig.4. Consistently, deep into parametric regions where the non-Bloch winding number W valued zero,no edge states show up,see Figs.5 and 6. Therefore,as shown in Figs.2 and 3,the resultant distributions of local decay probability Pmare asymmetric and back to normal.

5. Conclusions

In summary, we have investigated the single-particle continuous-time quantum walk on a finite bipartite non-Hermitian lattice with pure loss. Focusing on the resultant distribution of local decay probability Pm, an intriguing phenomenon is found, in which impressive population of the decay probability appears on edge unit cell although it is the farthest from the starting point of the quantum walker. Detailed numerical simulations reveal that the intracell hopping v of the lattice can be used to modulate the quantum walker to reach the leftmost unit cell,the rightmost unit cell,or none of them with a relative high portion of the probability. We then investigate the energy spectrum of the non-Hermitian lattice under open boundary condition. Edge modes are shown existing in the real part of the energy spectrum. Basing on its mathematical connection to a similar model,we show that the edge modes are well predicted by a non-Bloch topological invariant. The occurrence of conspicuous population of the local decay probability on either edge unit cell is closely related to the existence of edge states and their specific properties. The model could be experimentally realized with an array of coupled resonator optical waveguides along the line of Refs. [78,91]. The counterintuitive distributions shown in Figs.2 and 3 should be observed experimentally. The dynamics of the quantum walker running on such a non-Hermitian lattice behaves quite like a quantum switch. The mechanism may have prosperous applications in the designing of microarchitectures for quantum information and quantum computing in future.