大学数学课程中的HPM教学探索
2021-02-14蔡奇嵘
蔡 奇 嵘
(东华理工大学理学院,南昌 300013)
一、引言
HPM(History and Pedagogy of Mathematics),意指数学史与数学教育,HPM有两方面的含义:其一是指 HPM 国际研究团队在国际数学教育会议上专门讨论数学史和数学教育融合;其二是指这个团队的研究对象“如何更好地让数学史与数学教育融合在一起,共同促进学生的核心素养发展”[1]。
早在上世纪的八九十年代,有学者提出在未来的数学教育和研究中,必须越来越关注数学史有关的实证研究,这会给传统的数学教育带来意想不到的回报。2016年,在德国举行的ICIM-13(国际数学教育大会)中,HPM专题研究小组让我们看到了国外如何将数学史有机融入进教材中,包括在教学中的运用手段,史料的丰富性等方面,同时在研究的方式和内容方面也呈现出了更为多元化的趋势。
在大学数学的课程教学中,如何发展学生的数学能力,培养学生数学素养是当下数学教学工作者越来越重视的课题,其中数学文化的教学又起着至关重要的作用。数学史即为数学文化的一个重要体现,有利于培养学生的辩证唯物主义观点;让学生能根据所学习的内容追本溯源,了解整个知识体系的形成和发展;有助于培养学生的创新思维,体会数学的本质;提升数学课堂的魅力,让学生开阔视野,激发学习知识的兴趣,提高学生的数学文化素养。因此,如何将数学史更好地融入教学的研究已经成为当代数学教师关注的课题,同时,教师可以在进行HPM的教学实践过程中不断培养并完善数学学科的课程思政能力,广大数学教师也能够回归到探索数学教育的本质中去。
二、HPM视角下的教学案例
(一)与极限有关的教学
极限概念是高等数学中最为基础的概念之一,它的“ε-N”定义(“ε-σ”定义)也是大多数学生在学习高等数学过程中碰到第一个“拦路虎”,这种严密的逻辑化定义方式让学生最初接触时都有些不适应。教师在讲授极限概念的时候可以给学生简单介绍概念发展的历史,这样由浅入深、循序渐进的方式可以让学生更容易理解并接受。
极限概念的发展也经历一段非常漫长的过程,从最初的朴素直观的定义方式到现代严谨的理论定义,中间经过了两千多年的历程。我国早在公元前三世纪的《庄子·天下篇》中就有记载:“一尺之锤,日取其半,万世不竭”。我国数学家刘徽也在他的“割圆术”中将极限思想运用于实际,这于古希腊数学家所提出的“穷竭法”有异曲同工之妙。当然,这是极限概念的雏形。到十七世纪,英国数学家牛顿和德国数学家莱布尼茨创立了微积分,其中必定会涉及到极限思想,但他们也并没有明确提出极限概念,并且牛顿在极限概念的使用上是非常模糊不清的,甚至在某些关键之处出现了严重的逻辑错误,引发了数学史上的一次危机,数学家们开始意识到明确建立极限概念的必要性。经过数学家们漫长的探索,在十九世纪,法国数学家柯西和德国数学家维尔斯特拉斯终于完善了极限的定义,给出了极限定义的定性描述,即“ε-N”定义(“ε-σ”定义),极限的严格化定义对于建立微积分学的基础具有重大的意义。
教师在教授完极限定义之后,可结合数学史向学生介绍极限定义的应用。古希腊有位哲学家芝诺,一生以构想悖论而闻名,其中四个关于运动的悖论最著名,这里面第三个悖论“飞矢不动悖论”说到:任何一个物体待在一个地方叫不运动,可是飞动的箭在任意时刻不都是待在一个地方吗?这样的话,飞矢在任意时刻自然就是不动的。芝诺的论证看似简单有道理,但我们也清楚知道运动的本质是什么,要解决它就可以利用极限思想引入瞬时速度来说明。要求飞动的箭在某一时刻的瞬时速度,可以先求在这一时刻附近一个很小时间段内的平均速度,而这一时刻的瞬时速度就是当这个时间段Δt趋于零时平均速度所无限接近的那个数值,即极限值。有了瞬时速度的精确解释后,我们就可以反驳芝诺的悖论,飞动的箭除了在起点和终点之外,任意时刻的瞬时速度都不是零,也就是说它不是静止的。
(二)概率论的教学
概率论与数理统计是大学数学中的一门重要课程,我们都知道它与实际有着密切的联系,应用领域已渗透到现代科学和社会生活的每一个角落,可以说,我们的生活离不开概率论。为了让学生更好的了解并掌握概率论知识的具体应用,教师在可结合概率论相关数学史给学生讲授相关内容。

数学期望是概率论中的一个重要概念,学生在学习数学期望时,对其本质了解往往浮于表面,只生硬的记书本上的概念,要了解概率论是研究随机现象统计规律性的一门学科,我们在面对随机现象需要做决策时,依据的就是这个随机现象的数学期望。期望是基于概率基础上的,是对未知的预期,简单的说期望就是在多次实验之后,所预期的结果。教师在介绍完期望概念后,可给学生介绍概率论史上的一个有名悖论——“圣彼得堡悖论”:甲乙两人约定赌局,甲掷硬币直至掷出正面为止。若甲第一次就掷出正面,乙给甲1个卢布,若甲第一次掷出的为反面,第二次掷出正面,乙给甲2个卢布,若甲第一、二次均掷出反面,第三次掷出正面,乙给甲4个卢布……,以此类推,甲每多掷一次得到正面,乙就多付给甲一倍的钱。在这场赌博中,甲只赢钱不输钱,为保证游戏的公平性,甲需先付给乙一定的钱来保证乙不吃亏,那么,甲需先给乙多少前才能保证游戏的公平呢?在学习了数学期望后,学生们应该知道,甲应付的钱应该是他在这场赌局中赢钱的期望值,我们可以让学生来计算该期望值。若用X表示甲能赢得的钱数,则X的分布律如下表:

X124…2n-1…P1212 212 3…12 2…
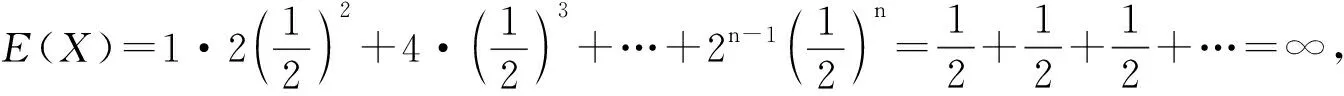
三、结语
近年来,我国的HPM教学研究不论是从理论体系还是具体实施模式都越来越成熟,并建立起了相应的规范、系统的体系。当然,这条路依然很漫长,还需要继续开发详尽实用且高质量的典型课堂案例,这就需要教师有良好的数学文化修养,同时,继续提高相应的HPM教学的技能,这仍然是我们不断努力的目标。
