张俊畅

(广东省大埔县虎山中学 514299)

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、构建模型，求解结论，验证结果并改进模型，最终解决实际问题.数学模型构建了数学与外部世界的桥梁，是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力.

我国《普通高中数学课程标准》中要求数学建模以不同的形式渗透于必修和选修课程中.数学建模进入高中数学课程已成必然，作为一线教师必须改变观念，积极探索数学建模教学实施策略，为学生数学学习营造更为宽广的空间.笔者通过数学史上的一道名题-米勒问题的数学建模与应用作些研究.

一、关于米勒问题

1471年，德国数学家米勒向诺德尔教授提出了如下十分有趣的问题：在地球表面的什么部位，一根垂直的悬杆呈现最长？即在地球上什么部位，视角最大？最大视角问题，是数学史上100个著名的极值问题中第一个极值问题，因而引人注目.因为德国数学家米勒曾提出这类问题，因此最大视角问题又称之为“米勒问题”.

二、米勒问题的数学问题形式

米勒问题可以转化为这样的几何模型：如图1，线段AB垂直于直线EF，垂足为点O，在直线EF上任选一点C，使得∠ACB的值最大，求此时点C的位置.

三、米勒问题的数学模型及其求解

1.米勒问题的代数解法

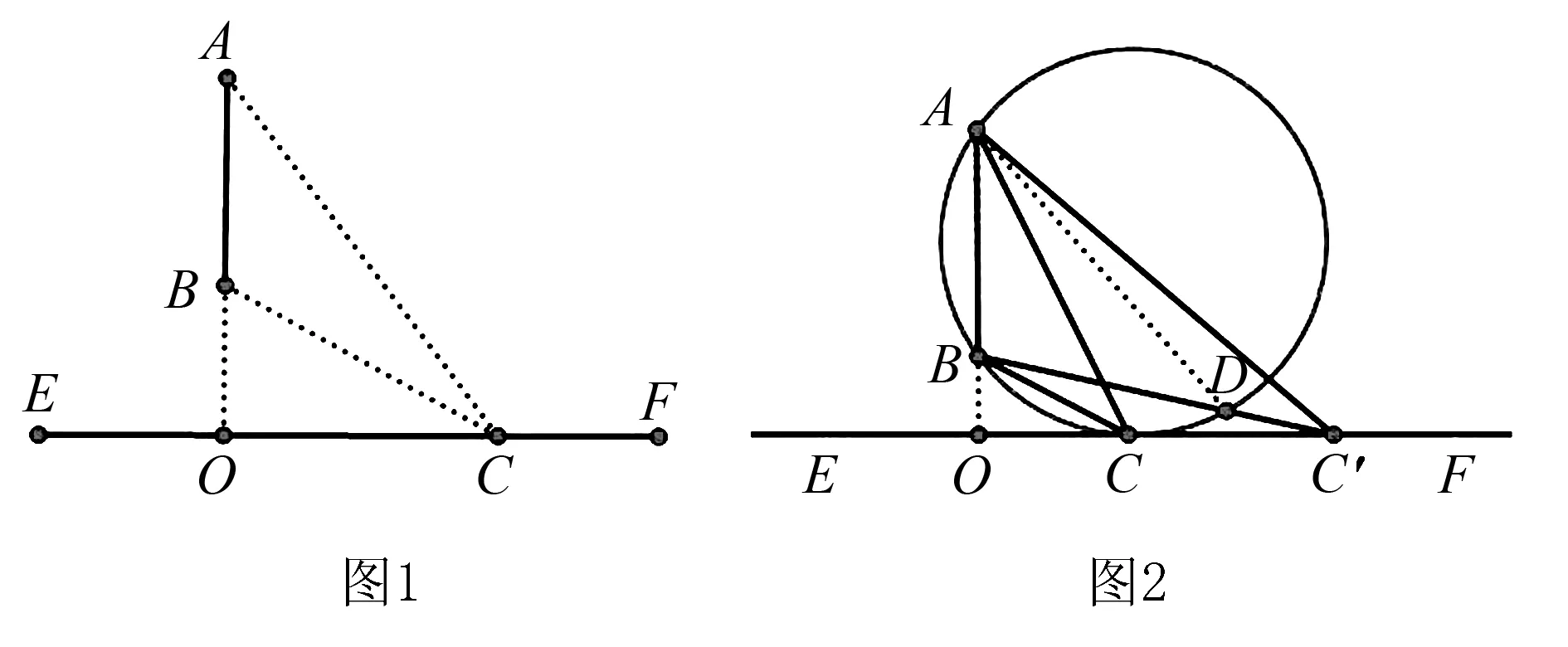
2.米勒问题的几何解法(Ad.Lorsch解法)

在水平直线上选择点C，使得△ABC外接圆与水平直线刚好相切于点C，则切点就是视角最大的点.

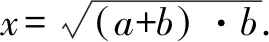
3.米勒问题的推广

如图3，已知点A,B是锐角∠MON的边OA上的两个定点，点C是边OM上的动点，则当点C在何处时，∠ACB最大？利用Ad.Lorsch的几何解法，我们不难发现:当△ABC的外圆与边OM相切于点C时，∠ACB最大(这里证明省略).

4.结论提炼

通过上面的数学建模的论证，我们可以得出如下重要结论(我们这里称为米勒定理)：

米勒定理已知点A,B是锐角∠MON的边ON上的两个定点，点C是边OM上的动点，则当且仅当△ABC的外圆与边OM相切于点C时，∠ACB最大.

四、米勒问题的应用

例1要测量电视塔AE的高度H(单位：m)，如图4，垂直放置的标杆BC的高度h=4m，仰角∠ABE=α,∠ADE=β,若该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d，使α,β之差较大，可以提高测量精度.若电视塔的实际高度为125m，试问d为多少时，α-β最大？

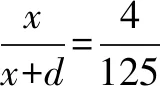
点评本题是以实际应用和平面几何为背景考查最大角问题，此解法以米勒定理和相似三角形等知识为突破口，结合方程思想求解，综合性强,能力立意高,有一定难度.

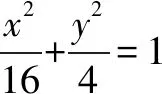
点评本解法不仅用到米勒定理的结论，而且还要熟悉定理证明的几何背景及图形间的内在联系，用相似三角形对应边成比例求线段比，运算量小解法简单快捷.

最大视角问题在数学竞赛、历届高考和模拟考试中频频亮相，常常以解析几何、平面几何和实际应用为背景进行考查.若能从题设中挖出隐含其中的米勒问题模型，并能直接运用米勒定理解题，这将会突破思维瓶颈、大大减少运算量、降低思维难度、缩短解题长度，从而使问题顺利解决.