田耀祖

(甘肃省通渭县第二中学 743300)

面积、体积是高中数学中的常见题型.此类问题的解答，通常利用给定的面积、体积公式，若给定图形的点的坐标，则如何求其面积或体积呢？除了化归于公式求解，是否能将面积与体积由点的坐标来公理化呢？经过笔者的深入思考、探究、尝试，终有一份收获.

定理1在平面内，已知△ABC，若A(x1,y1),B(x2,y2),C(x3,y3),则△ABC的面积

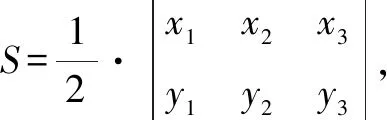
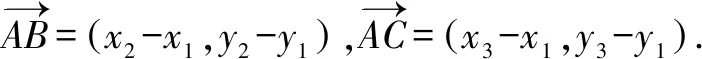
设x′=x2-x1,y′=y2-y1,x″=x3-x1,y″=y3-y1,

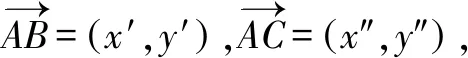
∵x′=x2-x1,y′=y2-y1,x″=x3-x1,y″=y3-y1，

记|x1y2+x2y3+x3y1-x2y1-x3y2-x1y3|

定理2 在空间内，已知△ABC，若A(x1,y1z1),B(x2,y2,z2),C(x3,y3,z3),则△ABC的面积

定理2的证明方法与定理1的很相似，只是将二维变元转化为三维变元就可以了.在此定理2的证明过程简略.

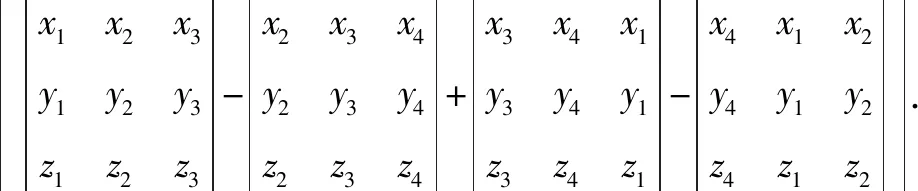
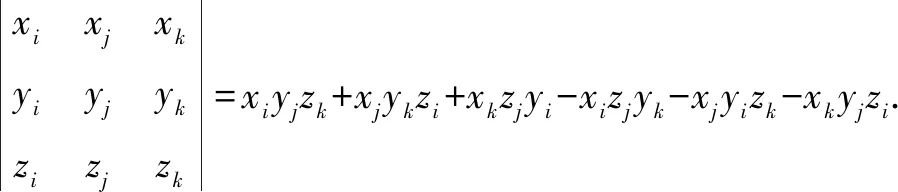
推论在空间中，已知四面体ABCD的顶点坐标分别是A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3),D(x4,y4,z4),那么四面体ABCD体积

上述坐标形式的求积公式，体现了顶点坐标与面积、体积的直接关系，并且此公式在形式上充分体现了数学的完美性、对称性.在内容上充分体现了数学的简捷性，规律性.更重要的是此公式在解决一些数学问题时表现出它优异的本色，能优化解题思维.下面举例说明它的应用.

一、解面(体)积的问题

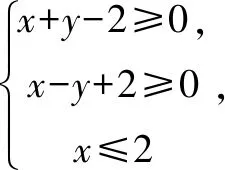
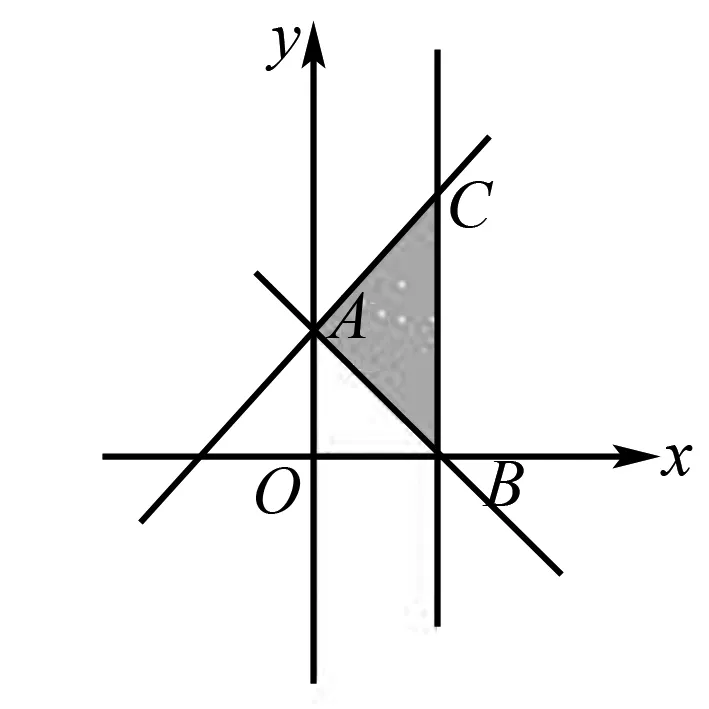
图1

解如图1所示,不等式组表示的平面区域是三角形ABC.而A,B,C点的坐标分别是A(0,2),B(2,0),C(2,4).

因此，答案是B.

二、解最值问题

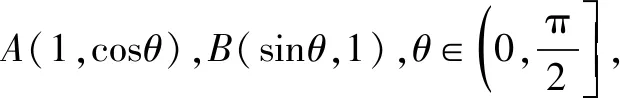
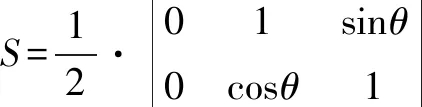
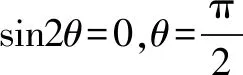
因此,答案为D.

例3在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A,B满足OA⊥OB.

△ABO的面积是否存在最小值?若存在，请求出最小值;若不存在，请说明理由.

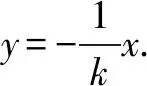
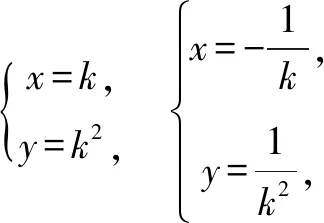
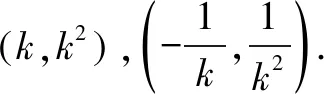
所以，△ABO的面积

∵k>0,

∴S≥1.

因此，△ABO面积S是存在的且最小值是1.

三、解共线、共面问题

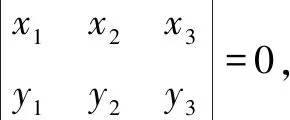
例4已知A(3,-6),B(-5,2),C(6,y)三点共线，则y=____.

解∵A,B,C三点共线,

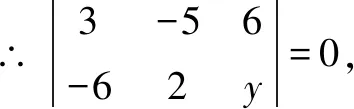
即|3×2+(-5)×y+6×(-6)-(-5)×(-6)-6×2-3×y|=0.

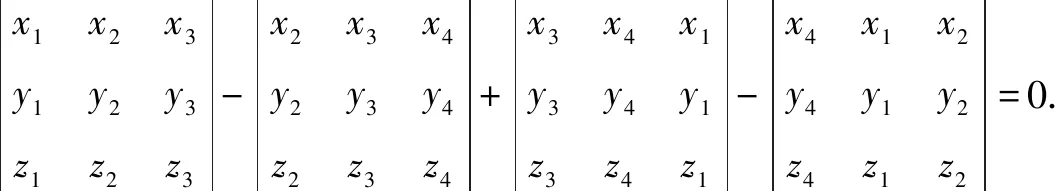
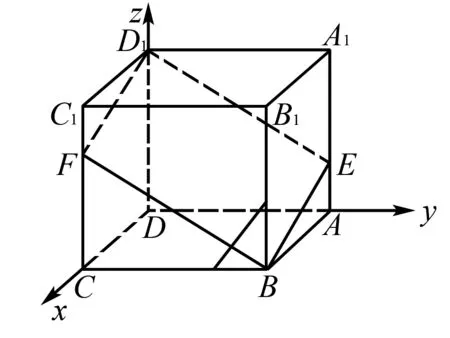
图2

例5如图，已知ABCD-A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，且AE=FC1=1，

求证：E,B,F,D1四点共面.

证明建立如图2所示的坐标系，则E,B,F,D1的坐标如下：

E(0,3,1),B(3,3,0),F(3,0,2),D1(0,0,3).

∴E,B,F,D1四点共面.

四、解点到平面距离的问题

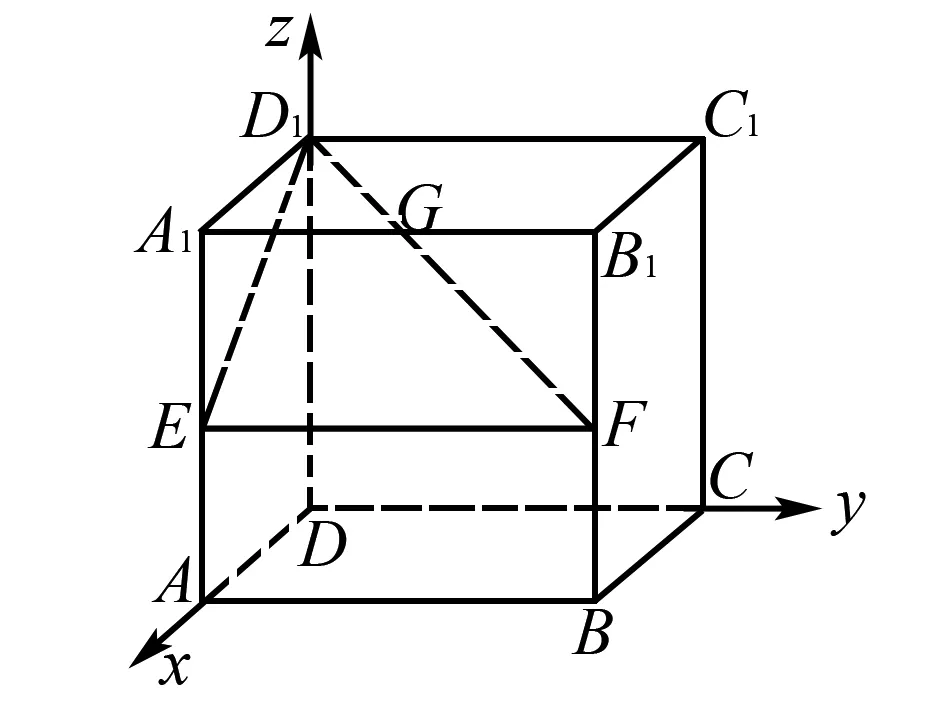
图3

例6在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别为棱AA1，BB1的中点，G为棱A1B1上的一点，且A1G=λ(0≤λ≤1)．则点G到平面D1EF的距离为( ).

2016年，我国教育部颁布了《中国高等教育系列质量报告》，其中显示国内高等教育“硬件”建设数量正在呈现井喷式增长发展趋势，根据统计目前全国固定资产也已经全面增加42.15%左右，在教学、科研仪器等方面更增幅超过60.22%。这些数据也在告诉人们高校教育领域已经引入了全新的固定资产管理方式，它基本实现了对校内固定资产管理的管理理念与系统功能数据的优化，值得期待。

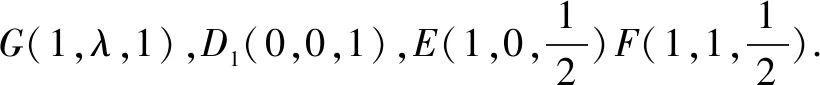
四面体的体积

底面D1EF的面积

因此，答案是D.

五、解异面直线夹角的问题

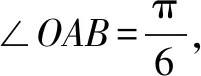
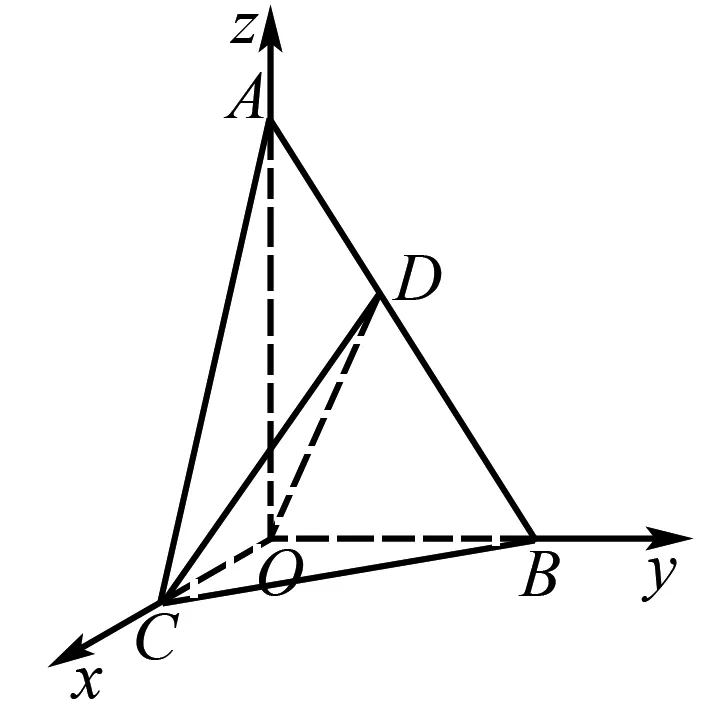
图4

求异面直线AO与CD所成角的大小．

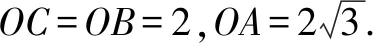
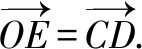
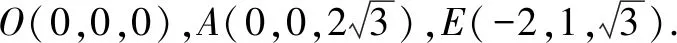
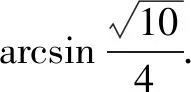
通过上述几例我们不难发现求积公式坐标化后，有它的优越性，不但解决一些面积、体积问题，而且还能解决一些立体几何的其它问题.所以运用好这一公式，将会优化解题的思维.