宋德银

(江苏省泰州中学 225300)

在圆锥曲线类型的题目中，构造法能很好地发挥学生的创造性思维.在应用构造法解决圆锥曲线时，我们要善于结合题目要求以及自身联想构造出满足条件的数学对象，使圆锥曲线题型的解法突破常规，另辟蹊径.

一、构造不等式求解参数范围

探求圆锥曲线中的参数取值范围是近几年高考考查的热点与难点，学生要善于深入题目条件，挖掘题中的隐含信息构建与参数有关的不等式或者不等式组，将题目所求问题转化为求解不等式或不等式组的问题.

(1)求椭圆C的标准方程；

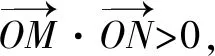
分析(1)当线段MN为长轴时，长度最长，4=2a，a=2，可得椭圆C的标准方程；(2)直线MN的斜率存在且不为0，设方程为y=kx+2，将其与椭圆的方程联立可得(1+4k2)x2+16kx+12=0，由Δ>0来构造不等式，并求解不等式，结合韦达定理求出直线OP斜率的取值范围．

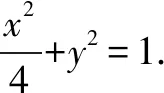
二、构造方程求解最值问题

对于圆锥曲线这类复杂的数学题，往往会出现自变量与因变量的概念，因此我们可以根据需要结合有利的数学条件来进行思路框架的设计.针对题目的未知参数，将有关的条件构成方程组，通过解方程组最终确定最值或是确定范围.

例3已知动圆C过点P(0，4)，且在x轴上截得的弦长为8．

(1)求动圆的圆心C的轨迹方程；

分析(1)设圆心C的坐标，及圆与x轴的其中一个交点M，由椭圆可得C的坐标之间的关系，即求出动圆C的轨迹方程；

(2)设A，B，Q的坐标，求直线AB的方程并与椭圆方程联立，构造方程组，求出两根之和及两根之积，由题意得|AD||BD|的表达式，由Q的坐标的范围求出其最大值．

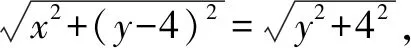
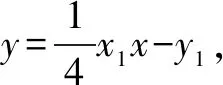
构造法善于利用题目的有利条件，将难以直接解决的参数问题转化到方程或函数等数学问题上来，便于学生理解，也能提高学生的解题效率.应用构造法解决圆锥曲线的问题，有助于学生理解圆锥曲线的实际应用.