朱启华 孙煜然 吴亭亭

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

考虑如下的一维Helmholtz方程:

(1)

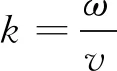
对于Helmholtz方程(1), 应用PML 技术将无界域截断为有界域, 得到带PML的Helmholtz方程

(2)

其中

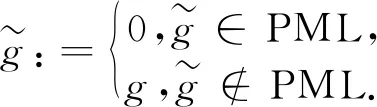
其中f0为震源主频, 一般取f0=25 Hz,LPML为PML 层的厚度,lx为匹配层的点到感兴趣区域与匹配层交界处的距离.a0为一正常数, 可取a0=1.79. 当在内部区域时,A≡C≡1, 此时带PML的Helmholtz方程(2)退化为Helmholtz方程(1).

目前, 数值求解Helmholtz方程的方法主要有有限元法[4-6]、有限差分法[7-10]等. 有限元法的精度高, 易于复杂边界条件和非均匀非结构化网格的处理, 但其计算量相对较大. 有限差分法的计算简单, 存储量小, 易于实现, 并且可以通过优化差分系数的方法来提高差分法的数值精度[1, 7, 9, 10].2013年,Chen等人[1]提出了带PML的Helmholtz方程的优化的9点有限差分法, 该格式为二阶格式. 2018年,Dastour等人[2]提出了带PML的Helmholtz方程的25点优化差分格式,该格式为四阶格式.文献[1]与[2]所研究的问题为二维Helmholtz方程. 2019年,Zhou等人[10]提出了一维Helmholtz方程的优化差分法, 该格式为二阶格式, 没有考虑吸收边界条件. 因此, 本文将重点研究一维带PML 的Helmholtz方程的四阶差分法. 首先, 针对一维带PML 的Helmholtz方程构造带参数的四阶差分格式, 并对差分格式进行相容性分析. 其次, 基于极小化数值频散的思想, 提出差分格式优化系数的整体选取策略和加细选取策略. 最后, 数值算例表明带加细参数的四阶差分格式提高了精度, 有效地抑制了数值频散, 在计算大波数问题时具有优势.

2 一维带PML的Helmholtz方程的四阶差分法

本节建立一维带PML的Helmholtz方程的四阶差分格式, 并对差分格式进行相容性分析与频散分析,提出差分格式的优化参数的整体选择策略和加细选择策略.

2.1一种相容的五点差分格式本小节建立与一维带PML的Helmholtz方程相容的五点差分格式.

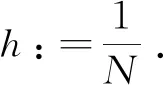
(3)

(4)

接下来, 建立零阶项k2Cu的四阶逼近. 借助于Taylor公式, 用五个点来建立k2Cu的四阶逼近. 为此, 令

lh(k2Cu)m:=c(k2Cu)m+dlh,0(k2Cu)m,

其中c+d=1. 然后, 用lh(k2Cu)来逼近k2Cu, 即

k2Cu|x=xm≈lh(k2Cu)|x=xm.

(5)

最后, 联立方程(4)与(5)得到方程(2)的一种相容的五点差分格式为

(6)

下面的定理1分析了差分格式(6)与带PML的Helmholtz 方程(2)的相容性.

定理1若d∈(0,1], 且满足c+d=1，则五点差分格式(6)与带PML的Helmholtz 方程(2)是相容的, 且为一种四阶差分格式.

证假设xm≤x≤xm+1, 则由Taylor展开式得

(7)

lh(k2Cu)|x=xm=k2Cu-ξ2h4+O(h6)，

(8)

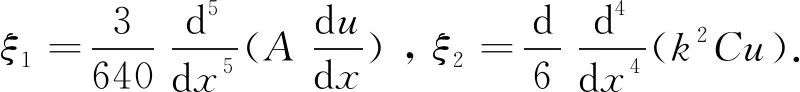
由(7)式与(8)式可知定理1结论成立.

为便于分析, 下面给出常波数情况下差分格式(6)在内部区域的具体形式. 由于在内部区域中A≡1,C≡1， 此时, 差分格式(6)可以写为

LhUm:=A1Um-2+A2Um-1+A3Um+A4Um+1+A5Um+2=gm，

(9)

其中

2.2数值波数与真实波数之间的误差分析在本小节, 给出差分格式(9)的频散方程, 并分析数值波数与真实波数之间的误差.

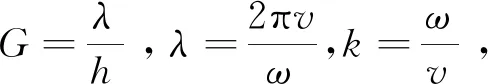
接下来, 将Ui:=eikx代入差分格式(9), 取gm=0, 并利用欧拉公式得频散方程为

2A1(2P2-1)+2A2P+A3=0.

(10)

在方程(10)中,将A1,A2,A3中的k用数值波数kN替换得[9]

(11)

基于方程(11), 下面的定理2给出了数值波数kN与真实波数k之间的误差分析.

定理2对于差分格式(9), 有

(12)

证令τ:=kh.又因为方程P依赖于τ, 故P(τ)=cos(τ). 进一步, 引入记号:

f1(τ):=cos2(τ)-8cos(τ)+7,

f2(τ):=-2dcos2(τ)+4dcos(τ)+3c+d.

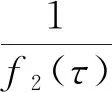
(13)

(14)

结合方程(11), (13)和(14)可得

上述定理2表明kN是k的四阶逼近. 此外, 与k5h4有关的项称为污染项, 它依赖于波数k和差分格式(9)中的参数d. 因此, 可以适当地选取d来使得kN更好地逼近k, 下一节将给出d的选取策略.

2.3五点差分格式的优化系数的选择策略在本小节, 基于极小化数值频散的思想, 给出差分格式(9)的优化参数的选择策略. 具体地, 极小化数值频散就是要极小化数值波数kN与真实波数k之间的误差. 研究表明, 差分格式(9)的数值频散越小, 其精度越高[1,7]. 如果差分格式具有最优的收敛阶, 并能够选择合适的参数来抑制数值频散, 就可以把它看作是带PML的Helmholtz方程的优化差分格式.

(15)

其中N:=P2-8P+7,D:=-2dP2+4dP+3-2d.

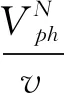
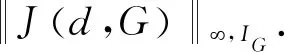
1) 策略1: 整体的参数选取方法.在给定的条件IG=[2.5,400] 下, 选取d∈(0,1]以满足

(16)

下面, 利用最小二乘法极小化目标函数的方法来实现整体的参数选择策略[1,7]. 若令J(d,G)=0,

通过整理可得

-8π2(P2-2P+1)d=G2(P2-8P+7)-12π2.

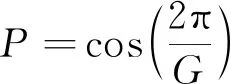
其中

该方程的系数矩阵有r行和1列, 是一个超定方程组. 选择r=100, 并用最小二乘法去解方程组得到差分格式(9)的一组优化参数为

c=0.898 5，d=0.101 5.

(17)

称带有参数(17)的差分格式(6)或(9)为Helmholtz 方程的整体五点差分格式(简称为global 5p).

整体的参数选取方法只给出一组优化参数, 这种做法比较粗糙. 为进一步提高差分格式的数值精度,下面给出加细的参数选取方法.

2) 策略2: 加细的参数选取方法.第一步：估计区间IG：=[Gmin,Gmax]；第二步：选取d∈(0,1]以满足(16)式.

加细的选取方法与整体的选取方法相比, 一个重要的区别在于区间IG是根据实际情况变化的. 在表1 中, 列出了多组加细的优化参数. 称带加细优化参数(以表1中的参数为加细优化参数)的差分格式(6)或(9)为Helmholtz方程的加细五点差分格式(简称为refined5p). 另外, 称带有参数c=1,d=0的差分格式(6)或(9)为Helmholtz方程的五点差分格式(简称为5pwithc=1,d=0).

表1 加细优化参数

为比较5pwithc=1,d=0,global5p和refined5p三种差分格式的数值频散, 图1和图2分别给出了这三种差分格式的标准化的数值相速度曲线图和标准化的数值群速度曲线图.global5p的数值频散相比5pwithc=1,d=0的数值频散有较大改善, refined5p的数值频散最小. 在数值算例中会进行更详细地比较.

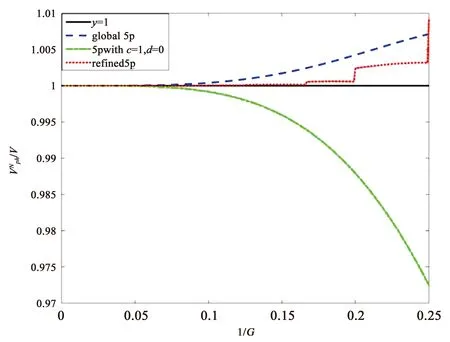
图1 三种差分格式的标准化的数值相速度曲线图

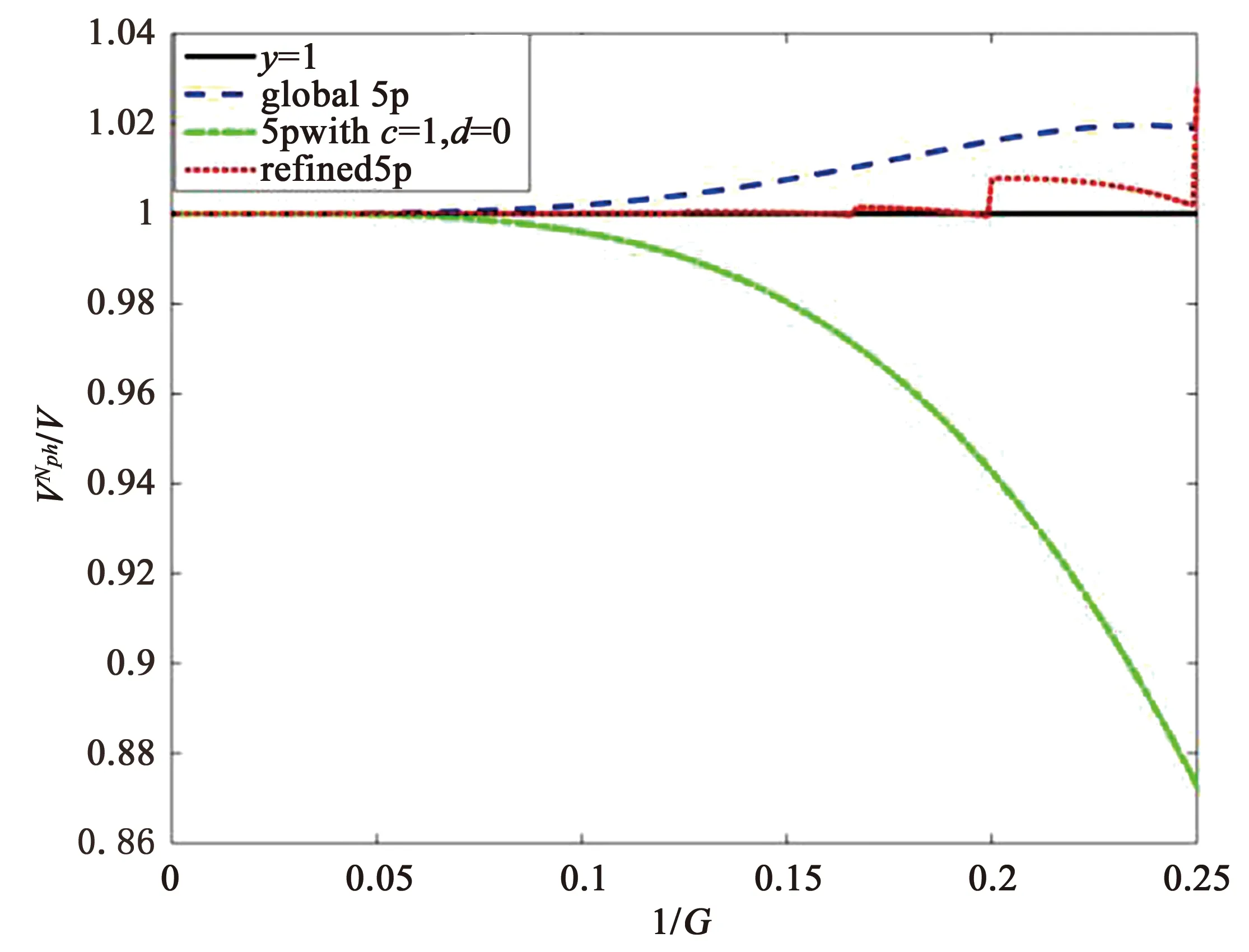
图2 三种差分格式的标准化的数值群速度曲线图

3 数值算例

为了验证本文所构造格式的有效性, 在本节中通过两个算例来进行数值验证.

算例1考虑如下一维Helmholtz方程：

该问题的真解为

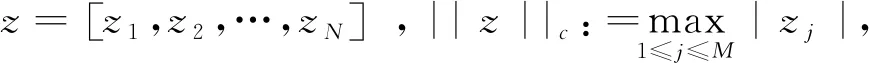
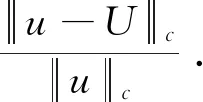
接下来, 需要对边界条件(20)进行四阶逼近. 为此, 由Taylor 公式展开得

将上述三个式子整理得

又由(18)式和(20)式可知

u(1)(xN)=iku(xN)，u(2)(xN)=-k2u(xN)+1.

故可得到边界条件(20)的近似为

对u(x1),u(xN-1)通过内插法进行五阶逼近,可得

表2与表3分别对应于k=800和k=1 000时, 不同的网格剖分所对应的三种差分格式的相对C-范数误差. 从表中可以看出, 对于相同的步长而言,refined5p的误差比global5p的误差和5pwithc=1,d=0的误差都要小,这说明了在这三种差分格式中refined5p的数值精度最高. 进一步, 图3和图4表明了上述三种格式均为四阶格式. 因此,refined5p相比其他两种格式有着更明显的优势, 尤其在计算大波数问题时.

表2 k=800时相对C-范数下的误差

表3 k=1 000时相对C-范数下的误差

图5分别给出了三种差分格式在kh=0.25,kh=0.5下的相对C-范数误差. 当kh固定时, 即表示每个波长内取的网格节点固定,refined5p比其他两种差分格式的误差要小. 不难发现, 当波数k由800增加到1 200时, 三种差分格式的误差也在增大. 但相对而言,refined5p的误差增大的比较缓一些, 从而更好地说明了refined5p的数值频散比5pwithc=1,d=0和global5p数值频散要小. 图5表明了本文所提出的差分格式refined5p可以更好地提高数值精度, 抑制数值频散.

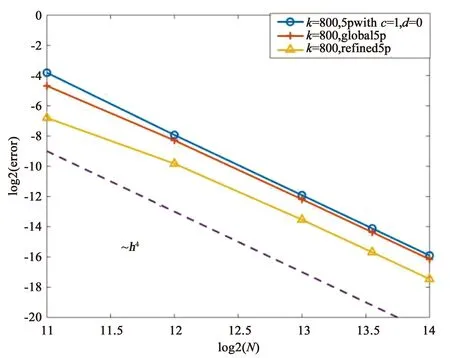
图3 k=800时相对C-范数下的误差

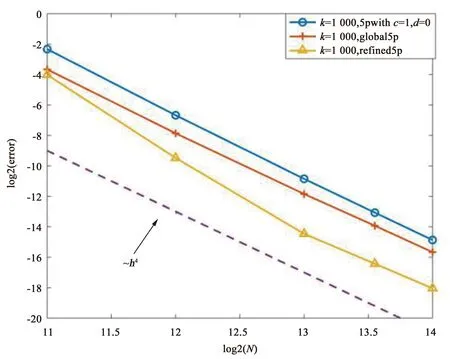
图4 k=1 000时相对C-范数下的误差

算例2考虑无界区域上的一维Helmholtz方程

-u″-k2u=δ(x-x0),x0=0,x∈(-,+)，

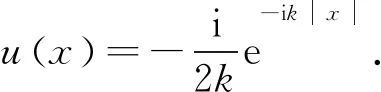
将无界域截断为有界域, 可借助于PML技术. 例如下面的方程

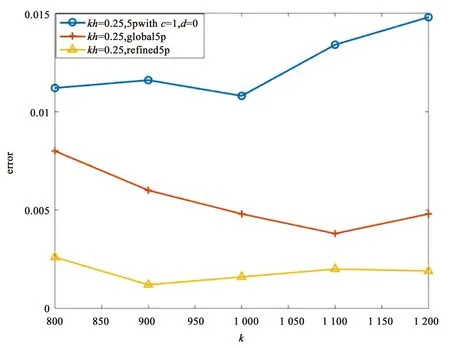
(a)kh=0.25

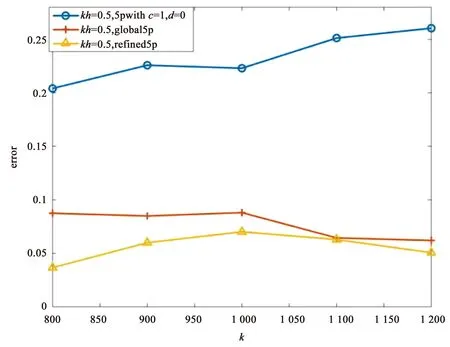
(b)kh=0.5图5 当k∈[800,1 200]时, 相对C-范数误差

假设感兴趣的区域为[-5,5], 可以选择优化系数(加细参数选取策略)并用差分格式(6)来求解问题(21)-(22). 在计算中, 采用相对L-范数和相对L2-范数来衡量误差. 具体地, 若设u为真解,U为数值解, 则

表4和表5分别给出了k=50,k=100, 取不同的步长时的相对L-误差与相对L2-误差以及收敛阶, 从表中可以看出, 当步长固定时, 相应的误差随着k的增大而增大. 进一步, 图6更好地说明了在不同相对范数的意义下, 差分格式均达到四阶.

表4 k=50时 相对L-范数和相对L2-范数及误差阶

表4 k=50时 相对L-范数和相对L2-范数及误差阶

表5 k=100时相对L-范数和相对L2-范数及误差阶

表5 k=100时相对L-范数和相对L2-范数及误差阶

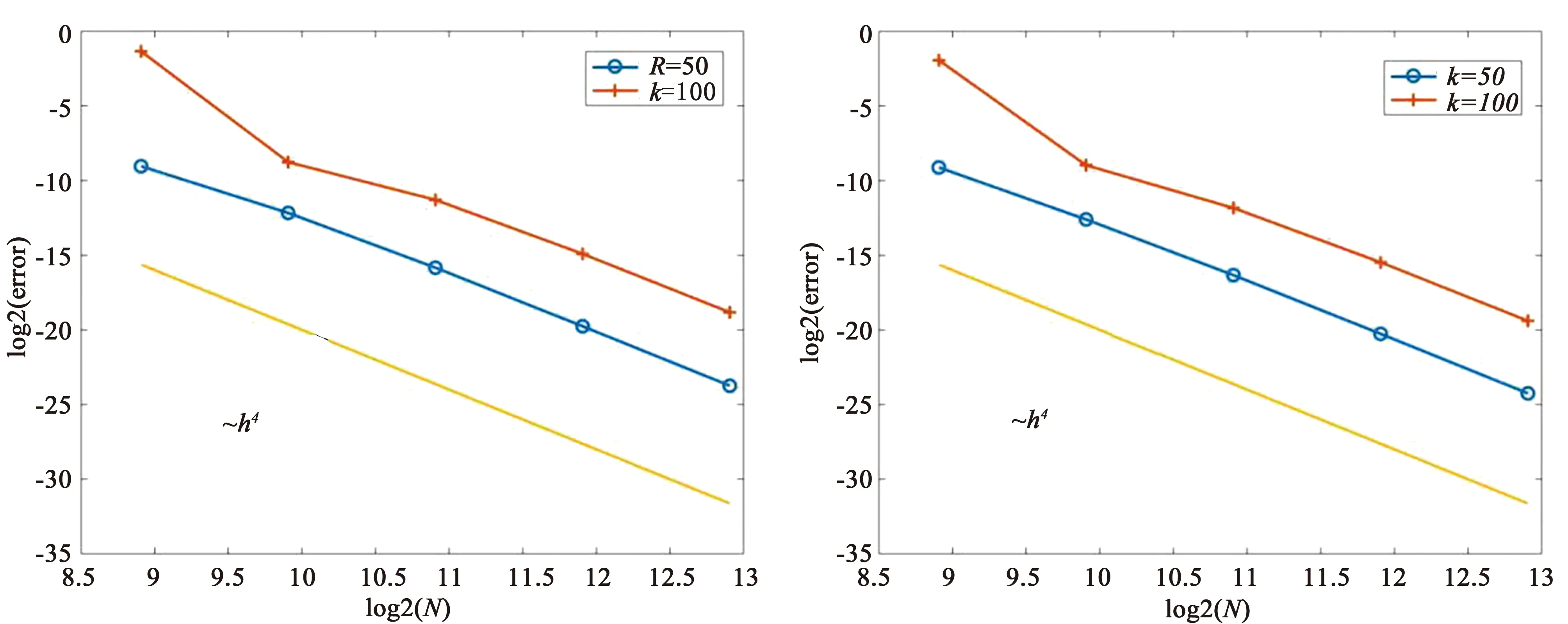
(a) 相对L-误差 (b) 相对 L2-误差图6 不同相对范数意义下的差分格式

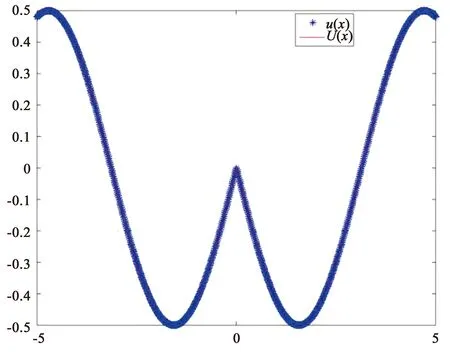
(a) k=1的精确解和取时所得数值解实部曲线

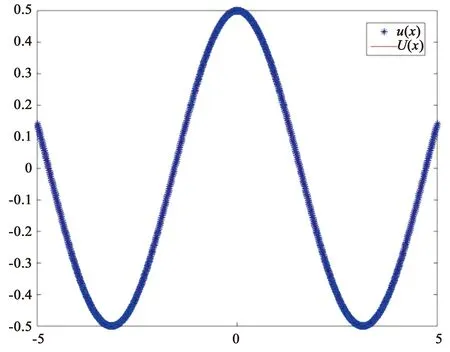
(b) k=1的精确解和取时所得数值解的虚部曲线图7 k=1时精确解与数值解曲线

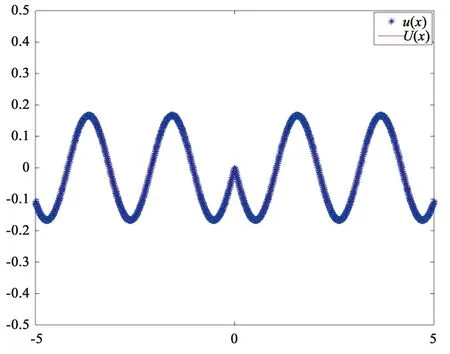
(a) k=3的精确解和取时所得数值解实部曲线图8 k=3时精确解与数值解曲线

(b)k=3的精确解和取时所得数值解的虚部曲线图8 k=3时精确解与数值解曲线

4 结 语

在本文中,给出了一维带PML的Helmholtz方程的五点差分格式, 该格式为四阶格式. 首先, 建立了带参数的五点差分格式, 并给出该格式的相容性分析. 接下来, 分析了数值波数和真实波数之间的误差. 然后, 基于极小化数值频散的思想, 提出了差分系数的整体优化选取策略和加细优化选取策略. 最后,通过数值算例验证了所提出的差分格式能够提高数值精度, 有效地抑制数值频散, 在计算大波数问题时具有显著优势.