李洪梅，姜冬勤，王平心

(1.江苏科技大学 计算机学院,江苏 镇江 212003;2.江苏科技大学 理学院,江苏 镇江 212003)

0 引言

聚类分析是数据挖掘与机器学习领域中的重要技术之一[1-2],已经广泛地应用于多个领域,包括信息粒化[3-4]、图像处理[5]、生物信息学[6]、安全保障[7]、网页搜索[8]等。所谓聚类就是将数据集中的样本划分到不同的类簇中,使得相同类簇中的样本相似度高,而不同类簇中的样本相似度低。聚类作为一种无监督学习技术,在识别无标签数据结构方面发挥了极大的作用。针对不同的情况,可以将聚类方法粗略地分为两大类:层次聚类方法和划分聚类方法[9]。

传统的聚类方法大多属于硬聚类,即对象要么属于一个类,要么不属于一个类,聚类的结果必须具有清晰的边界。但是在处理不确定性信息时,考虑到当前获取到的信息还不够充分,强制将其中的元素划分到一个类中,往往容易带来较高的错误率或决策风险。为了解决传统聚类方法存在的问题,许多新的聚类策略被提出。Hoppner等人[10]将模糊数学引入到了聚类分析中,用模糊集表示聚类结果。Lingras[11-12]提出了粗糙聚类方法,将聚类结果由粗糙集的正域,边界域和负域来表示。以上方法都是对传统硬聚类的一种改进。而三支决策聚类方法[13],是将三支决策[14]思想引入到了聚类分析中,将确定的元素放入核心域中,将不确定的元素放入边界域中延迟决策,有效地降低了决策风险。三支聚类不仅可使聚类的结果具有更好的结构特征和可解释性,还可以避免二支决策引起的不必要代价。因此研究基于三支决策的聚类分析具有非常广泛的科研价值和实际应用价值。

自从三支聚类方法提出以来,很多学者在这个理论框架下发展了多种三支聚类算法, Afridi等人[15]提出了一种使用博弈论粗糙集模型处理缺失数据的三支聚类方法;Wang和Yao[16]提出了一种基于收缩和膨胀的三支聚类框架,称为CE3,该框架来自数学形态学的腐蚀和膨胀的思想;Yu等人[17]研究通过低秩矩阵实现主动三支聚类方法。王等人[18]利用动态邻域给出了一种基于邻域的三支聚类算法。以上的研究成果均丰富了三支聚类理论和模型,扩大了其应用范围和领域。

2019年,Li和Qian等[19]研究了聚类集成的样本稳定性的概念并用来发现稳定关系的样本集并建立基于样本稳定性的集成聚类算法。该方法基于一组聚类结果,计算任意两个样本被划分在同一类的频率,即样本的共现概率。当两样本的共现概率为1时,说明这两个样本始终在同一类;当两样本的共现概率为0时,说明这两个样本始终不在同一类;无论共现概率为1还是为0,都说明两样本之间具有较高的稳定关系。而共现概率介于0和1之间的样本说明在某些聚类结果是聚在一类,在另外的聚类结果没有聚在一类,他们之间的关系具有一定的不确定性。为了定量的刻画样本的稳定性,文献[19]提出了确定性函数的概念来刻画两样本的确定度并将一个样本与其他样本的平均确定度定义为样本的稳定性。稳定性比较高的样本在聚类过程中有着较好类属关系,而稳定性较低的样本在聚类过程中类属关系较为不确定。基于样本稳定的理论,最近李等[20]给出了一种基于信息熵的样本稳定性度量函数。

样本的稳定性理论为研究样本间关系的不确定性提供了新思路,同时也为三支聚类中核心样本和边界样本的判别提供了一个新依据。将稳定性的概念和三支聚类方法结合起来,可以提供一种有效的寻找三支聚类核心域和边界域的方法。本文利用样本稳定性理论给出一种新的三支聚类方法,其主要思想是将任意两个样本的邻域中的公共元素个数定义两个样本的共现概率,并在此基础上定义每个样本的稳定性。然后基于阈值将这些样本元素分为稳定样本集和不稳定样本集。对稳定集中的样本,我们采用传统方法挖掘其团簇结构。对于不稳定集中的样本,我们通过比较样本到稳定集中聚类中心的距离将它们分到相应类的边界域中。通过以上策略,我们得到了三支聚类的核心域和边界域。

0.1 三支聚类

三支聚类方法是对二支聚类即硬聚类方法的拓展,对于二支聚类分析的基本概念可以总结为:假设给定数据集U={x1,x2,…,xn}中包含n个样本对象,数据集的聚类数为k,获得聚类结果是C={C1,C2,…,Ck}。则聚类结果中任意类簇需要满足以下三个条件:

(1)Ci≠ø,i=1,…,k;

(3)Ci∩Cj=ø,i≠j。

条件(1)要求任意类簇不为空。条件(2)和条件(3)要求任意样本对象x∈U有且仅属于一个类簇。在这种情况下,任意类簇之间有着清晰的界限且每个类簇Ci只是数据集U中的一个分区。

受到三支决策理论的启发,Yu等人[17]提出了三支聚类分析理论。三支聚类结果与硬聚类结果的区别是:使用一对集合来表示一个类簇即Ci=(Co(Ci),Fr(Ci))。硬聚类结果中每个样本对象至多属于某个类簇,而将那些可能属于多个类簇的样本即不确定类簇的样本强制划分到某个类簇中可能降低聚类精度。但是三支聚类结果考虑了那些不确定类簇归属的样本,显然,样本对象和类簇之间存在三种关系即:确定属于该类簇、不属于该类簇、可能属于该类簇。对比可以看出,使用三个域来表示一个类簇更合适,即核心域、边界域以及琐碎域。其中Co(Ci)⊂U、Fr(Ci)⊂U、Tr(Ci)=U-(Co(Ci)∪Fr(Ci)),这三个集合分别表示类簇的核心域、边界域以及琐碎域。这三个子集需要满足以下几个条件:

(1)Tr(Ci)∪Co(Ci)∪Fr(Ci)=U,

(2)Co(Ci)∩Fr(Ci)=ø,

(3)Co(Ci)∩Tr(Ci)=ø,

(4)Fr(Ci)∩Tr(Ci)=ø。

如果Fr(Ci)=ø,则类簇Ci=Co(Ci)且Tr(Ci)=U-Co(Ci),此时该聚类结果是一个硬聚类结果。通过单个集合(边界域中无样本对象时)来表示一个聚类结果是三支聚类结果的一个特殊情况。

聚类结果中的核心域和边界域需要满足不同的要求,在本文中,我们要求核心域和边界域满足以下三个条件:

(1)Co(Ci)≠ø,

(3)Co(Ci)∩Co(Cj)=ø,i≠j。

条件(1)要求任意类簇不能为空。条件(2)要求数据集U中的任意样本对象至少属于某个类簇中的核心域或者边界域,可能存在某个样本元素x∈U属于多个类簇的情况。条件(3)要求不同类簇之间的核心域是没有交集的。基于上述讨论,得出三支聚类结果表达方式,

C={(Co(C1),Fr(C1)),

(Co(C2),Fr(C2)),…,

(Co(Ck),Fr(Ck))}。

数据集中的每个样本至多属于一个类簇中的核心域而至少属于一个类簇中的边界域。

0.2 稳定性

文献[19]利用样本的共现概率和确定性函数,给出了样本稳定性的定义。其中样本的共现概率是基于一组聚类结果,利用两个样本划分在同一类的频率得到的。 共现概率为1 的样本表明样本始终被分在一类,具有较高的稳定性。同理共现概率为0 的样本表明样本始终没有被分在一类,两样本之间具有较高的稳定性,而共现概率介于0和1之间的样本说明在某些聚类结果是聚在一类,在另外的聚类结果没有聚在一类。为此,文献[19]给出了确定函数的概念来评价样本关系的确定度,并用一个样本与其他样本的平均确定度来定义样本的稳定性。

定义1[19](确定性函数)设t为区间[0,1]的一个常数。样本的确定性函数为关于变量p的函数f,其中p∈[0,1],,定义如下:

(1) 如果pt,f′(p)>0，

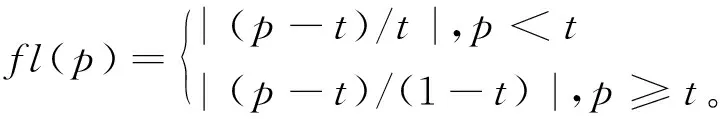
(1)

定义2[19](样本稳定性)假定一个数据集X={x1,x2,x3,…,xn}含有n个样本,pij表示样本xi与xj的共现概率,基于确定性函数f,对于每一个点xi,我们可以定义样本稳定性s(xi)如式(2)。

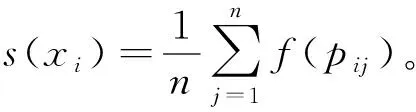
(2)

特别的,针对线性函数fl(p),样本点xi的稳定性记为sl(xi),其计算方法见式(3)。

(3)

1 基于邻域样本稳定性的三支聚类

1.1 基于邻域样本稳定性的定义

在样本稳定性的定义中,样本的共现概率pij起着关键的作业,如何定义样本的共现概率pij是一个非常重要的问题。文献[20]采用两样本K近邻中共同元素的个数与K的比值作为它们的共现概率。对数据集X={x1,x2,x3,…,xn},记样本xi的K近邻为KNN(xi),则KNN(xi)满足:

1)KNN(xi)⊂X;

2) |KNN(xi)|=K;

3) ∀xj∈KNN(xi),xk∈X-KNN(xi),有

dist(xi,xj)≤dist(xi,xk)。

对于样本xi与xj,基于K近邻的共现概率pij定义为公式(4)。

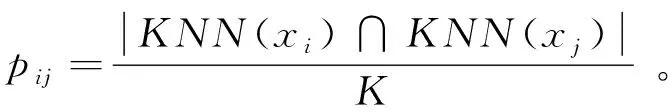
(4)

下面我们用一个例子来说明样本共现概率的计算。设X={x1,x2,x3,…,x6},它们之间的距离关系用如表1所示。

表1 X样本间的距离关系

利用基于K近邻的共现概率的定义,设K=3,我们可以得到样本间的共现概率如表2所示。

表2 样本间的共现概率

共现概率为1的样本表明样本始终被分在一类,具有较高的稳定性。同理共现概率为0的样本表明样本始终没有被分在一类,两样本之间具有较高的稳定性,而共现概率介于0和1之间的样本说明在某些聚类结果是聚在一类,在另外的聚类结果没有聚在一类。因此当我们得到样本间的共现概率以后,我们还需要学习阈值t,使得稳定性函数在t的值最小。这里我们采用Otsu算法[21]来求t。

1.2 基于邻域样本稳定性的三支聚类算法

(5)

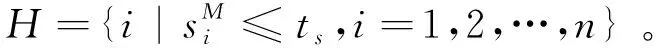
(6)

其中集合O代表比较稳定的数据样本,H代表不稳定的数据样本。对稳定的数据样本集合我们采用传统硬聚类kmeans算法得到聚类结果Ci作为三支聚类的核心域。而对于不稳定的数据样本集合,采用遍历的形式,依次计算环中的每个数据到聚类中心的距离d,随后我们先找出距离最小的值dmin,将此距离最小的所对应的数据点划分为此类的上界,然后计算此点到其他聚类中心的距离与dmin的差值dpoor,如果这个距离dpoor小于指定的阈值p,则把此数据点划分为该类的上界,直至不稳定的数据样本集合中数据全部遍历完成。最终得到三支聚类结果。算法步骤如算法1所示。

算法1:基于邻域样本稳定性的三支聚类 输入:数据集X={x1,x2,x3,…,xn},邻域大小K,聚类数目k。输出:C={(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…(Co(Ck),Fr(Ck))}Step1:利用公式(4)求得每两点共现概率pij并通过Otsu算法来求t;Step2:利用公式(3)可以得到每个样本的稳定性,记SM={sM1,sM2,…,sMn};Step3:利用Otsu算法应用到SM求得阈值ts;Step4:利用公式(6)和(7)求得稳定的数据样本集O和不稳定的数据样本H;Step5:对稳定性的数据进行kmeans聚类得聚类结果Ci,i=1,2,…,k。Step6:对不稳定的数据H, for i=1,2,3,…,|H| do 计算不稳定点hi到每一个聚类C的聚类中心的距离d={d1,d2,..,dk} 找出集合d中的最小值dmin=min(d), 将dmin对应的数据hi划分到其对应类C的上界。 接着,计算集合d中其余点与dmin的差值dpoor if dpoor

2 聚类结果评价指标

2.1 准确率

准确率(Accuracy)[22]是一种常见的评价聚类结果好坏的外部指标。这个方法就是根据预测的结果与真实值做对比,当此值越高说明聚类结果越好。

定义1[22](ACC)

其中N表示总样本个数,Ci表示正确划分到类i的样本个数,k表示聚类数。本论文的三支聚类算法实验所计算的ACC是使用核心域的对象来计算的。

2.2 Davies-Bouldin Index评价指标

Davies-Bouldin Index,即DB-Index[23]。由Davide L.Davies和Donald W.Bouldin于1979年提出来的,是一种内部聚类评价指标。DBI的主要思想是度量每个簇类最大相似度的均值。

定义2[23](DBI)

3 实验结果

为了验证算法的有效性,本文采用5组UCI数据对算法进行验证,UCI数据集的纯度高,噪音数据较少,被许多人所认可。数据集如表3所示,本文将基于邻域样本稳定性的三支聚类与传统的聚类k-means和FCM进行ACC与DBI聚类指标的对比,实验结果如表4所示,其中邻域大小K取为样本个数与类别数2倍比值的整数部分。

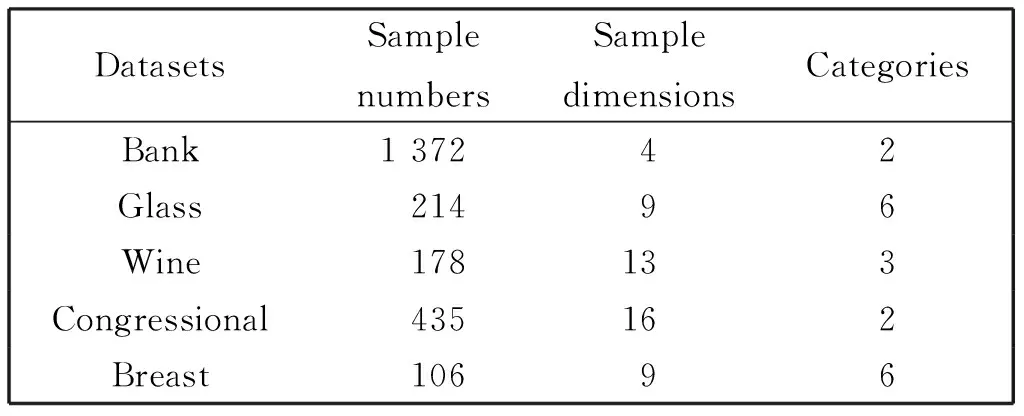
表3 实验中使用的数据集

表4 UCI数据集上的实验结果

通过比较表4的实验结果不难发现,除了在数据集Bank上,本文给出的基于样本邻域三支聚类ACC略低于k-means和FCM外,其他数据集合指标上,本文给出的基于样本邻域稳定性的三支聚类总体性能比k-means算法均有一定的提升: DBI变小,准确率提高。因而,本文的基于邻域样本稳定性的三支聚类可以提高聚类精度,改善聚类性能,能够更好地显示出聚类的结构。

4 结论

本文利用样本邻域给出了一种基于样本邻域稳定性的三支聚类算法。该算法使用任意两个样本的邻域中的公共元素个数定义两个样本的共现概率,并在此基础上定义每个样本的稳定性,然后基于阈值将这些样本元素分为稳定样本集和不稳定样本集。对稳定集中的样本,我们采用传统方法挖掘其团簇结构。对于不稳定集中的样本,我们通过比较样本到稳定集中聚类中心的距离将它们分到相应类的边界域中。实验也表明此方法可以提高聚类的精度。

在本文的算法中,邻域大小K是本算法中一个非常重要的参数,如何设置参数K将是未来的研究内容之一。