GLOBAL OPTIMIZATION OF THE DIFFERENCE OF TWO INCREASING PLUS-CONVEX-ALONG-RAYS FUNCTIONS∗
2021-01-07SHAHRIARIPOUR
H.SHAHRIARIPOUR
Department of Mathematics,Graduate University of Advanced Technology,Kerman,Iran
E-mail:hakimeh-shahriari@yahoo.com
H.MOHEBI†
Department of Mathematics and Mahani Mathematical Research Center,Shahid Bahonar University of Kerman,P.O.Box:76169133,Postal Code:7616914111,Kerman,Iran
E-mail:hmohebi@uk.ac.ir
Abstract The theory of increasing and convex-along-rays(ICAR)functions defined on a convex cone in a real locally convex topological vector space X was already well developed.In this paper,we first examine abstract convexity of increasing plus-convex-along-rays(IPCAR)functions defined on a real normed linear space X.We also study,for this class of functions,some concepts of abstract convexity,such as support sets and subdifferentials.Finally,as an application,we characterize the maximal elements of the support set of strictly IPCAR functions and give optimality conditions for the global minimum of the difference between two IPCAR functions.
Key words increasing plus-convex-along-rays function;support set;maximal element;global minimum;DC-function
1 Introduction
The theory of abstract convexity,also called convexity without linearity,is a powerful tool that allows us to extend many facts from classical convex analysis to more general frameworks.It has been the focus of active research for the last fifty years because of its many applications in functional analysis,approximation theory,and nonconvex analysis.Nevertheless,just like convex analysis,the development of abstract convexity has been mainly motivated by applications to optimization.The works[2,5–8,13,16,17,22,27,31–33,38,41]use abstract convexity for applications to nonconvex optimization.A deep study on abstract convexity can be found in the seminal book of Alex Rubinov[34];see also the monograph of Ivan Singer[40].Abstractconvexity reflects one of the fundamental concepts of convex analysis,which is the fact that every lower semicontinuous convex functionfis the upper envelope of affine functions[24,42].More precisely,at every pointx,we have
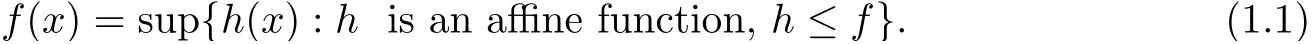
Most results in convex analysis are consequences of two important aspects of(1.1):(i)the“supremum”operation,and(ii)the set over which this supremum is taken.Results that depend on aspect(ii)are likely to depend on specific properties of linear/affine functions.How does one distinguish which facts from convex analysis follow from the“upper envelope“operation,and which follow from the particular structure of the set of linear/affine functions?Abstract convexity is the fundamental tool that addresses this crucial question:it retains the“upper envelope”operation in aspect(i)of(1.1),but changes the set of functions over which the supremum is taken.These sets of functions are called abstract linear functions and they naturally induce the abstract affine sets.Since aspect(i)of(1.1)is retained,global properties of convex analysis may be preserved even when dealing with nonconvex models.Thus,this approach is sometimes called a“non-affine global support function technique”(see,for example[13,34]).Many tools from convex analysis,such as subgradients andε-subgradients,have their“abstract”counterparts,obtained again by using abstract linear functions.For instance,the abstract subgradient of an abstract convex functionfat a pointxcollects all the supporting abstract linear functions which are minorants of(i.e.,their graphs stay below)f,and coincide withfatx.This extends the concept of the convex subgradient and provides a valuable tool for studying certain nonconvex optimization problems(see[13,32,34]).Another example is the Fenchel-Moreau conjugatef∗of a functionf.The definition off∗uses the set of linear functions,and abstract convexity allows one to produce“abstract”types of conjugates.
Abstract convexity has found many applications in the study of problems of mathematical analysis and optimization.Also,it has found interesting applications to the theory of inequalities.Abstract convexity opens the way for extending some of the main ideas and results from classical convex analysis to much more general classes of functions,mappings and sets.It is well-known that affine functions play a crucial role in classical convex analysis.Therefore,in abstract convexity,the role of the set of affine functions is taken by an alternative setHof functions(so-called elementary functions),and their upper envelopes constitute the set of abstract convex functions(or,H-convex functions).Different choices of the setHgenerate variants of the classical concepts,and have been shown to have important applications in global optimization(see[28–31]).Moreover,if a family of functions is abstract convex for a specific choice ofH,then we can use some key ideas of convex analysis in order to gain new insight on these functions.On the other hand,by using an alternative set for affine functions,we identify those facts in classical convex analysis which depend on the specific properties of affine functions.
Abstract convexity has mainly been used for the study of point-to-point functions.Examples of its use in the analysis of multifunctions can be found in the works of Levin[14,15],who focused in the study of abstract cyclical monotonicity,and also Penot[23],who,by using a framework of generalized convexity,showed the existence of a convex representation of a maximal monotone operator by a convex function which is invariant with respect to Fenchel’s conjugacy.
We recall that some classes of increasing functions are abstract convex;for example the class of increasing and positively homogeneous(IPH)functions[19]and the class of Increasing and convex-along-rays(ICAR)functions[35]are abstract convex.The first studies of these functions were carried out over cones in topological vector spaces[6,7].Some suitable extensions of this class of functions defined over the whole of a topological vector spaceXwere obtained in[5,20,21].
One of the most important global optimization problems is that of minimizing DC-functions(difference of two convex functions),i.e.,

wherefandgare real valued convex functions defined on RnandXis a subset of Rn.In the general case,DC-functions can be replaced by DAC-functions(difference of two abstract convex functions).It is quite natural that we study various classes of monotonic functions in terms of“abstract convexity”.In particular,some authors have considered abstract convexity as a main tool in the study of increasing positively homogeneous functions(IPH),increasing convexalong-rays functions(ICAR),decreasing convex-along-rays functions(DCAR)and increasing co-radiant functions(ICR)[3,4,18,19,29];in addition,we can consider abstract convexity as a main tool for studying of increasing and plus-convex-along-rays(IPCAR)functions.It is worth noting that minimizing the difference of two increasing and positively homogeneous(IPH)functions[19],minimizing the difference of two topical functions[3],minimizing the difference of two increasing and radiant(IR)functions[18]and minimizing the difference of two increasing and co-radiant(ICR)functions[4]were all studied as global optimization problems of minimizing DAC-functions.Also,Rubinov and Glover gave optimality conditions for the difference of two ICAR functions in[29];the results obtained have found many applications in various areas of mathematical economics,optimization theory and game theory[1,10–12,26,37].In fact,one of the applications was given in[26],which examined the generalized nonlinear penalization by using increasing and positively homogeneous convolution functions.Moreover,in mathematical economics,in the study of moral hazard principal-agent problems,the agent’s expected utility can be a rational function of strictly IPH functions(for more details,see[25]).We can use the minimizing of the difference of two strictly IPH functions to minimize this rational function.Indeed,if
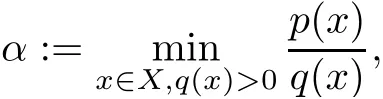
wherep,qare non-negative strictly IPH functions defined onX,then the functionp−αqis a difference of two strictly IPH functions(note that sinceα>0,then,αqis a strictly IPH function).Therefore there are enough motivations for us to study the class of increasing and plus-convex-along-rays(IPCAR)functions by using“abstract convexity”as a main tool.In this case,we replacefandgby two increasing plus-convex-along-rays(IPCAR)functions in(1.2),and characterize the abstract convexity,the support sets and the subdifferentials of this class of functions.Moreover,we present various characterizations of the maximal elements of the support set of strictly IPCAR functions.Finally,as an application,we give optimality conditions for the global minimum of the difference of two IPCAR functions.Because IPCAR functions have some properties close to those of topical and sub-topical functions[36],they have many applications in various parts of applied mathematics,in particular,in the modelling of discrete event systems and in the study of some problems of mathematical economics and game theory,and also in the study of inequality systems involving increasing functions[9–12,36].
The paper has the following structure:in Section 2,we first collect some definitions,notations and preliminary results related to IPCAR functions and abstract convexity,and give some characterizations of abstract convexity,support sets and the subdifferentials of IPCAR functions.In Section 3,we give characterizations of the maximal elements of the support set of strictly IPCAR functions and,as an application,we present optimality conditions for the global minimum of the difference between two IPCAR functions.
2 Preliminaries

is convex(concave).
A functionf:X−→R is called increasing if(x,y∈Xwithx≤y=⇒f(x)≤f(y)).We also say that a functionf:X−→R is strictly increasing if(x,y∈Xwithx Definition 2.3A functionf:X−→R is called IPCAR iffis increasing and has plus-convex-along-rays,and called IPCEAR iffis increasing and has plus-concave-along-rays.Moreover,a functionf:X−→R is called strictly increasing plus-convex-along-rays(strictly IPCAR)iffis strictly increasing and has plus-convex-along-rays. In what follows,we consider the classQof all real valued increasing plus-convex-along-rays functions defined onX.We now describe some properties of this class of functions. (i)Iff,g∈Q,thenf+g∈Q. For eachy∈Xand eachα∈R,we define the functionψy,α:X−→R byψy,α(x):=ψ(x,y,α)for allx∈X. It follows from Remark 2.1 that the set{λ∈R:λ≥α,y+λ1≥x}is nonempty and bounded in R,and soψis a real valued function.Clearly,this set is a closed subset of R.It is worth noting that the functionψis a generalization of the min-type functions which were defined on Rnin[36,39]. Remark 2.4It should be noted that one of the main results of convex analysis asserts that an arbitrary lower semicontinuous convex functionfis the upper envelope of the setUof its affine minorants(elementary functions): for allx=(x1,···,xn),y=(y1,···,yn)∈Rnand allα∈R.Therefore,ψy,αis a min-type function in the sense of[36,39]. We now provide some properties of the functionψin the following proposition: Proposition 2.5Letψbe as in(2.2).Then,for eachx,x′,y,y′∈Xand eachα,α′∈R,one has Theorem 2.11Letf:X−→R be a function.Then the following assertions are equivalent: (i)fis IPCAR. (ii)fyis convex on R,fy(λ)≥f(x)for allx,y∈Xand allλ∈R such thaty+λ1≥x. (iii)fyis convex on R,fy(ψy,α(x))≥f(x)for allx,y∈Xand allα∈R. Proof(i)=⇒(ii)Letx,y∈Xandλ∈R be such thaty+λ1≥x.Sincefis IPCAR,thenfy(λ)=f(y+λ1)≥f(x),andfyis convex on R. (ii)=⇒(iii)Letα∈R andx,y∈Xbe arbitrary.In view of(2.12),we havey+ψy,α(x)1≥x.This,together with the hypothesis(ii)(withλ:=ψy,α(x)),implies thatfy(ψy,α(x))=f(y+ψy,α(x)1)≥f(x). (iii)=⇒(i)Letx,y∈Xbe such thaty≥x.Then we conclude from(2.7)and the hypothesis(iii)thatf(y)=fy(0)=fy(ψy,0(x))≥f(x),sofis increasing. The proof of the next result is similar to the one of Theorem 2.11,and therefore we omit it. Theorem 2.12Letf:X−→R be a function.Then the following assertions are equivalent: (i)fis IPCEAR. (ii)fyis concave on R,fy(λ)≤f(x)for allx,y∈Xand allλ∈R such thaty+λ1≤x. (iii)fyis concave on R,fy(ϕy,β(x))≤f(x)for allx,y∈Xand allβ∈R. Definition 2.13([34])LetDbe a set of functions fromXinto R.We recall that a functionp:X−→R is called abstract convex(or,D-convex)if there exists a subsetD0ofDsuch that Remark 2.19One of the main notions of convex analysis,which plays a key role in various applications,is the subdifferential.There are two equivalent definitions of a subdifferential for a convex function.The first of them is based on the global behaviour of the functionf:a linear functionℓis called a subgradient(i.e.,a member of the subdifferential)of the functionfat a pointx0if the affine functionh(·):=ℓ(·)−(ℓ(x0)−f(x0))is a support function with respect tof,i.e.,h≤f.The second definition has a local nature and is connected with a local approximation of the function:the subdifferential is a closed convex set of linear functionsℓsuch that the directional derivative off, is the upper envelope of this set.For a differentiable convex function these two definitions represent the support and tangent sides of the gradient,respectively. The various generalizations of the second definition have led to the development of a rich theory of nonsmooth analysis.The natural field for generalizations of the first definition is abstract convexity.We now give the definition of the abstract subdifferential for abstract convex functions as follows:the abstract subgradient of an abstract convex functionfat a pointx0collects all the supporting abstract linear functions which are minorants of(i.e.,their graphs stay below)f,and coincide withfatx0.This extends the concept of the convex subgradient and provides a valuable tool for studying certain nonconvex optimization problems(see[13,32,34]).Some properties of abstract subdifferentials and their applications were given in[13,34].Moreover,the sum rule for abstract subdifferentials has been proved under suitable conditions in[13]. Definition 2.20([34])Letf:X−→R be an IPCAR function(note that in view of Theorem 2.14,fis abstract convex with respect to the setH,which is defined by(2.26)).A functionψy,α∈His called an abstract subgradient(or,H-subgradient)offat a pointx0∈Xif The set of all abstract subgradients offatx0is called the abstract subdifferential(or,Hsubdifferential)offat the pointx0,and is defined by Example 2.21([34])LetXbe a locally convex Hausdorff topological vector space.LetH:=X∗(the dual space ofX)be the set of all real-valued continuous linear functionals defined onX.Then,f:X−→(−∞,+∞]is anH-convex function if and only iffis lower semicontinuous and sublinear.Also,fis anHL-convex function if and only iffis lower semicontinuous and convex,whereHLis the set of all continuous affine functions defined onX.Therefore,the abstract subdifferential(or,H-subdifferential)for a convex functionf:X−→(−∞,+∞]is exactly the classical convex subdifferential wheneverH:=X∗(the dual space ofX).In fact,the abstract subdifferential is an extension of the convex subdifferential. Remark 2.22Letf:X−→R be an IPCAR function.Define Clearly,E(f,H)⊆A(f,H),whereA(f,H)is defined by(2.28). In what follows,we show that theH-subdifferential of an IPCAR function is nonempty,i.e.,iff:X−→R is an IPCAR function,then∂Hf(x)≠∅for eachx∈X. Proposition 2.23Letf:X−→R be an IPCAR function,and letx0∈X.Then In this section,by using the results obtained in Section 2,we first present characterizations of maximal elements of the support set of IPCAR functions.Finally,as an application,we give the necessary and sufficient conditions for global minimizers of the difference between two IPCAR functions.We start with the following definition: Definition 3.1([34])Consider a setUof real valued functions defined on a setZ.We assume thatUis equipped with the natural(pointwise)order relation of functions.Recall that a functionf∈Uis called a maximal element of the setUif Clearly,supp(f,H)⊆A0(f,H).Indeed,ifψy,α∈supp(f,H),thenψy,α(x)≤f(x)for allx∈X.Putx:=y+α1,and so,by(2.6)and Definition 2.2,we conclude thatα≤f(y+α1)=fy(α).Thus,ψy,α∈A0(f,H).Hence,supp(f,H)⊆A0(f,H).It is clear that ifψy,α∈supp(f,H)is a maximal element ofA0(f,H),then it is also a maximal element of supp(f,H). Now,by extra conditions on the IPCAR functionf:X−→R,we show that the converse statement to Proposition 3.4 holds. Proposition 3.6Letf:X−→R be a strictly IPCAR function,and lety∈Xbe such thatε:=max{α∈R:fy(α)≥α}<+∞.Suppose that Assumption(S)holds for the functionf.Thenψy,εis a maximal element ofA0(f,H)if and only iffy(ε)=ε. ProofFirst note that since,by the hypothesis,fy(ε)≥ε,it follows thatψy,ε∈A0(f,H).Now,due to Proposition 3.4,we only need to show that iffy(ε)=ε,thenψy,εis a maximal element ofA0(f,H).To this end,letψy′,ε′∈A0(f,H)be such that By using Proposition 2.9,we conclude that We claim thaty=y′.If we were to suppose not,then in view of(3.8),y′ Corollary 3.7Letf:X−→R be a strictly IPCAR function such thatεy:=max{α∈R:fy(α)≥α}<+∞for ally∈X.Suppose that Assumption(S)holds for the functionf.Then,for eachψy,α∈A0(f,H),there exists a maximal elementψy′,α′ofA0(f,H)such thatψy,α(x)≤ψy′,α′(x)for allx∈X.In this case,one can takey′:=y+εy1−fy(εy)1andα′:=fy(εy). ProofLetψy,α∈A0(f,H)be given.First,clearly,fy′(α′)=f(y+εy1−fy(εy)1+fy(εy)1)=fy(εy)=α′,so,ψy′,α′∈A0(f,H).In view of the hypothesis,it is clear that Proposition 3.8Letf,g:X−→R be IPCAR functions,and letεy:=max{α∈R:fy(α)≥α}<+∞for ally∈X.Suppose that Assumption(S)holds for the functiong.Then the following assertions are equivalent: (i)A0(f,H)⊆supp(g,H). (ii)gy(εy)≥εyfor ally∈X. Proof(i)=⇒(ii)Suppose that(i)holds.Lety∈Xbe arbitrary.Then,in view of the definition ofεy,one hasfy(εy)≥εy,and soψy,εy∈A0(f,H).Thus,by the hypothesis(i),ψy,εy∈supp(g,H)=A0(g,H)(because Assumption(S)holds for the functiong).This implies thatgy(εy)≥εy. (ii)=⇒(i)Letψy1,α1be an arbitrary element ofA0(f,H).Therefore,fy1(α1)≥α1,and hence, This implies thatψy2,α2∈A0(g,H)=supp(g,H)(because Assumption(S)holds for the functiong).Therefore,in view of(3.16),it follows thatψy1,α1∈supp(g,H),which completes the proof. We are now ready to give necessary and sufficient conditions for global minimizers of the optimization problem(3.1).We start with the following lemma: Lemma 3.9Letf,g:X−→R be IPCAR functions.Then Proof(i)Suppose thatf(x)≤g(x)for allx∈X.Then it is clear that supp(f,H)⊆supp(g,H).Conversely,assume,if possible,that there existsx0∈Xsuch thatf(x0)>g(x0).Sincefis an IPCAR function,it follows from Theorem 2.3 and Remark 3.2 that This,together with the fact thatf(x0)>g(x0),implies that there existsψy0,α0∈supp(f,H)such thatψy0,α0(x0)>g(x0).This implies thatψy0,α0/∈supp(g,H),which is a contradiction,because,by the hypothesis,supp(f,H)⊆supp(g,H).Hence,f(x)≤g(x)for allx∈X. (ii)Suppose thatA0(f,H)⊆supp(g,H).Thus,by Remark 3.2,supp(f,H)⊆supp(g,H).Therefore,in view of(i),we conclude thatf(x)≤g(x)for allx∈X. (iii)Assume that Letψy,α∈A0(f,H)be arbitrary.Hence,α≤fy(α)=f(y+α1).Putx:=y+α1in(3.17). Therefore,we obtain that and so the proof is complete. Theorem 3.10Letf,g:X−→R be IPCAR functions,and letεy:=max{α∈R:fy(α)≥α}<+∞for ally∈X.Suppose that Assumption(S)holds for the functionsfandg.Then the following assertions are equivalent: (i)x0∈Xis a global minimizer of the optimization problem(3.1). (ii)The following inequality holds: (iii)We have∂Hf(x0)⊆∂Hg(x0)and supp(f,H)⊆supp(g,H)−h(x0),whereh:=g−f. We conclude this section with the following definition: Definition 3.15([36])A subsetWofXis called upward ifx∈X,w∈Wandw≤x,then,x∈W. We now give a sufficient condition for which Assumption(S)holds.Lemma 3.16Letf:X−→R be an IPCAR function,and let Assume that supp(f,H)is an upward set andψy,εy∈supp(f,H)for ally∈X.Then Assumption(S)holds. ProofIn view of Remark 3.2,supp(f,H)⊆A0(f,H).Conversely,letψy,α∈A0(f,H)be arbitrary.Thus,fy(α)≥α,and so,by the definition ofεy,we have thatα≤εyand thatfy(εy)≥εy.Putα1:=fy(εy)andy1:=y+(εy−fy(εy))1.This implies thatα≤α1andy1≤y.Therefore,by Proposition 2.9, Sinceεy≤α1,it follows from(2.5)thatψy1,εy(x)≤ψy1,α1(x)for allx∈X.This,together with(2.4)and the fact thaty1≤y,implies thatψy,εy(x)≤ψy1,εy(x)≤ψy1,α1(x)for allx∈X.Thus,ψy,εy≤ψy1,α1onX.Since,by the hypothesis,supp(f,H)is upward andψy,εy∈supp(f,H),we conclude from Definition 3.15 thatψy1,α1∈supp(f,H).Hence,in view of(3.33),ψy,α∈supp(f,H),which completes the proof.Note that supp(f,H)⊆H,and also,we consider onHthe natural(pointwise)order relation of functions,whereHis defined by(2.26). Remark 3.17It should be noted that the converse statement to Lemma 3.16 is not true.Indeed,consider Example 3.12.It is easy to check that ify>0,then by using Remark 2.4, This implies thatψy,εy/∈supp(f,H)for ally>0,while Assumption(S)holds.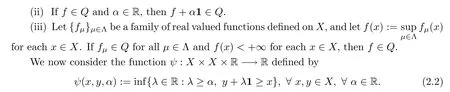

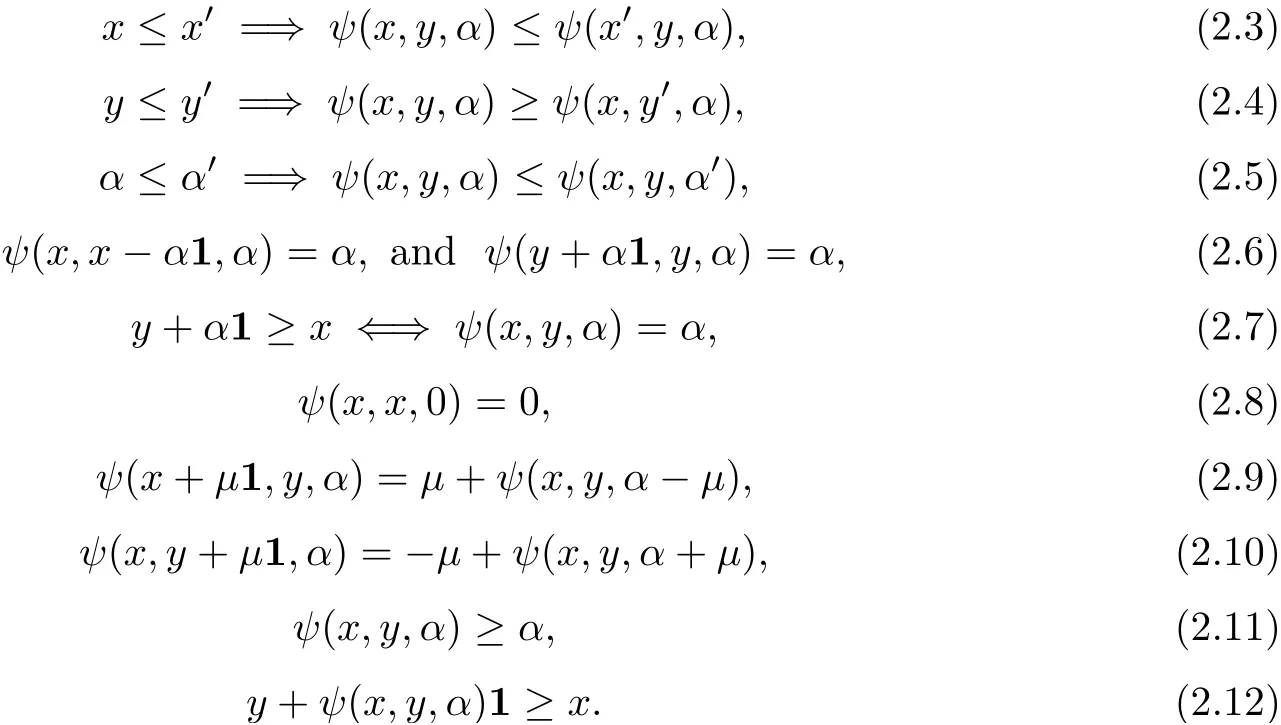






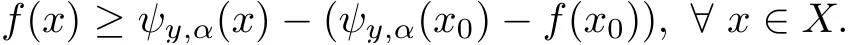




3 Characterizing Global Minimizers of the Difference Between two IPCAR Functions







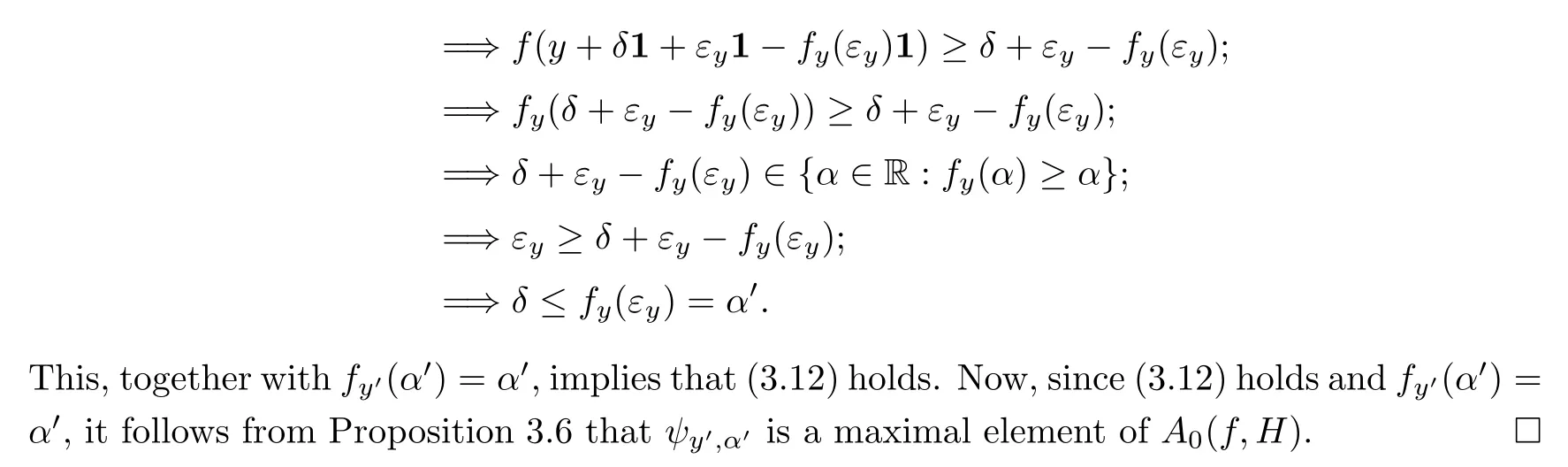
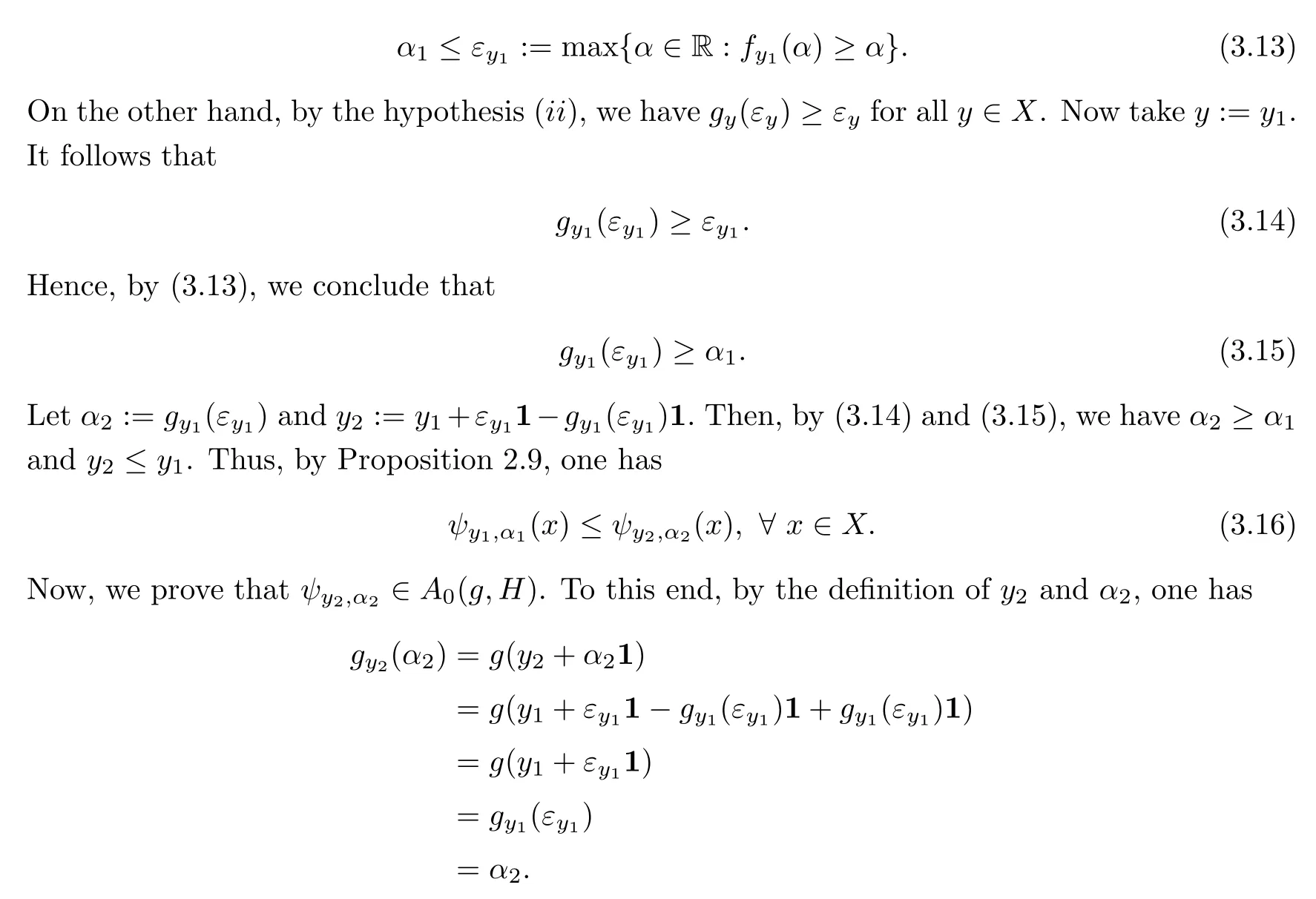
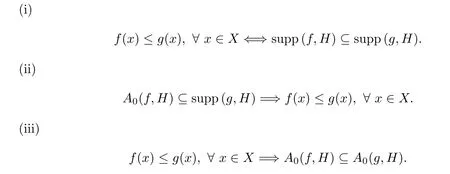
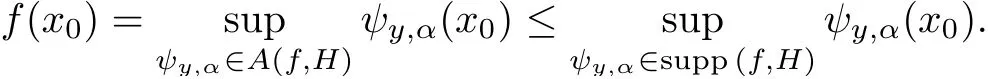

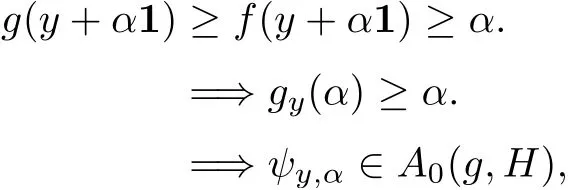
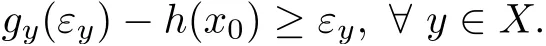





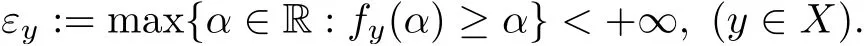

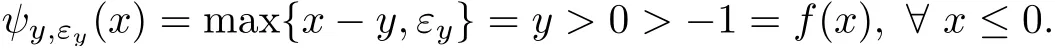
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- CONTINUITY PROPERTIES FOR BORN-JORDAN OPERATORS WITH SYMBOLS IN H¨ORMANDER CLASSES AND MODULATION SPACES∗
- ASYMPTOTIC STABILITY OF A BOUNDARY LAYER AND RAREFACTION WAVE FOR THE OUTFLOW PROBLEM OF THE HEAT-CONDUCTIVE IEAL GAS WH SY*
- ON REFINEMENT OF THE COEFFICIENT INEQUALITIES FOR A SUBCLASS OF QUASI-CONVEX MPPG RL L RB*
- EXISTENCE OF SOULUTIONS FOR THE FRACTIONAL (p,q)-LAOLACIAN PROBLEMS INVOLVING A CRITICL SOBLEV EXPNN*
- RADIALLY SYMMETRIC SOLUTIONS FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING NONHOMOGENEOUS OPERATORS IN AN ORLICZ-SOBOLEV SPACE SETTING∗
- ON VORTEX ALIGNMENT AND THE BOUNDEDNESS OF TH Lq-NORM OF VIRUICITY IN INCOMPRESSBLE VU FUD*
