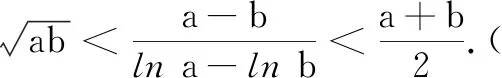李 鑫 胡雪文

(湖南省长沙市第一中学,410005)

一、试题呈现

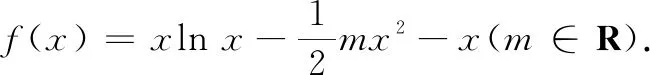
(1)若f(x)在(0,+∞)单调减,求实数m的取值范围;

(2)若f(x)在(0,+∞)存在两个极值点x1,x2,且x12.

二、学生解答

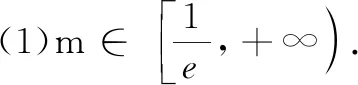
当m≤0时,g′(x)>0,g(x)单调增,g(x)在(0,+∞)最多有一个零点,从而f(x)在(0,+∞)最多有一个极值点,不合题意.

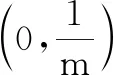
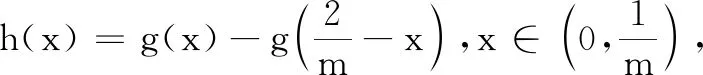
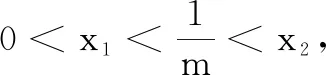
综上，lnx1+lnx2>2.

三、错因分析

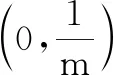
四、解法探究

极值点偏移问题近年来一直是解题研究的热门问题,常见的有三种处理方式:构造函数法、换元法与对数均值不等式法.下面从三个方面探究解决该问题.

探究1构造函数法

解法1依题意，lnx1-mx1=0，lnx2-mx2=0,即lnx1=meln x1，lnx2=meln x2， 所以lnx1,lnx2为方程x=mex的两个相异实根.

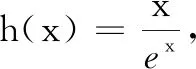
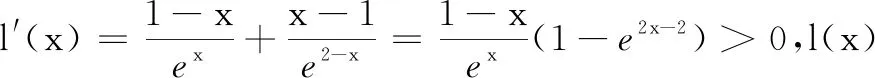
又lnx1<1

因为lnx2,2-lnx1∈(1,+∞),h(x)在(1,+∞)单调减,所以lnx2>2-lnx1,亦即lnx1+lnx2>2.

评注要证lnx1+lnx2>2,可将lnx1,lnx2看成一个整体,将mx化为meln x,将lnx当成变量构造新函数h(x).求导后发现h(x)的极大值点为1,最后利用h(x)的单调性来证明不等式.一般地,要证明x1+x2>(<)2x0(x0是f(x)的极值点),构造函数h(x)=f(x)-f(2x0-x),利用单调性来证明时一定需要确保函数f(x)的极值点x0是实数,不含参数才行.

探究2换元法

本题为含参数的极值点偏移问题,题目中除了x1,x2外还含有参数m,因此可以尝试消去参数,转化为不含参数的问题去解决；或者以参数为媒介,构造一个变元的新的函数来处理.

综上，lnx1+lnx2>2成立.

探究3对数均值不等式法

从要证明不等式的结构出发,可以尝试利用对数均值不等式来证明.

解法3依题意，lnx1-mx1=0，lnx2-mx2=0,所以

lnx1+lnx2=m(x1+x2)，

①

lnx1-lnx2=m(x1-x2).

②

因为m>0(同上文解答可知m≤0不合题意),所以lnx1+lnx2>2成立.

评注对数均值不等式本质是将对数函数lnx进行放缩,最终达到化繁为简、化难为易,快速解决问题的目的.