赵少卿,崔 岩,周六圆,孙 观,何宏骏

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引言

混沌是一种看似无序的复杂运动形态，是不同于周期态、平衡态和拟周期态的特殊状态。20世纪60年代,气象学家洛伦茨(Lorenz)发现了一个由一阶非线性三耦合微分方程组产生的混沌轨迹[1-2]。20世纪70年代，混沌现象引起学界的广泛重视，多种混沌系统应运而生，例如，与Lorenz系统有着不同拓扑结构的Chen系统[3]、可以用物理手段实现的Chua电路系统[4]和Lü系统[5]等。勒斯勒(Rössler)系统是基于Lorenz系统提出的具有较好混沌行为的非线性方程组[6]。近年来，文献[7]对Rössler系统进行了动力学分析，为该系统拓展了可选择的参数范围。文献[8]实现了Rössler系统与Sprott-O系统的混沌反同步，使Rössler系统在工程实际中的应用更为广阔。

非线性系统是输入和输出不成正比的系统。混沌是非线性系统的最典型行为，它源于对初始条件的敏感依赖性[9]，对初值的微小扰动将会给系统带来较大的影响。关于Rössler系统，文献[10]研究了一种基于Rössler系统的二次加密算法。文献[11]通过对Rössler系统运动轨迹的跟踪，使得心脏搏动系统产生混沌现象。文献[12]基于后推(Backstepping)算法，通过控制器使得超混沌Rössler系统的李雅普诺夫(Lyapunov)函数为负，实现对系统的稳定性控制。文献[13]用滑模变结构方法控制Rössler混沌系统，并使得趋近速度可自适应调节，从而提高了状态变量的收敛速度。文献[14]将Lorenz和Rössler系统进行耦合，研究了两种时滞系统的耦合同步问题，揭示了系统中的时滞和耦合对系统动力学的影响。文献[15]通过数学分析，对Rössler系统的余维二fold-Hopf分岔进行了研究。文献[16]实现了对Rössler系统的双反馈控制，并得出在平衡点发生Hopf分岔的充分条件。时滞系统是在系统变量中加入时滞参量使信号传输发生延时的系统。时滞系统中的Hopf分岔现象对系统的稳定性有较大影响。文献[17]研究表明：时滞可使系统产生较为稳定的吸引子。文献[18]采用改良的一阶差分算法，一定程度上减少了时滞Lorenz系统的计算量。文献[19]通过数值分析法分析了时滞反馈对Lorenz系统稳定性的影响。

本文依据非线性动力学和Hopf分岔理论，对时滞Rössler系统进行分析，给出系统的Hopf分岔发生条件，得出了系统在时滞分岔点附近的稳定性分布。在计算过程中，针对存在的平衡点非零问题，采用换元法简化计算过程，得到了比较理想的数值分析结果和仿真结果。

1 Rössler系统分析

Rössler系统为：

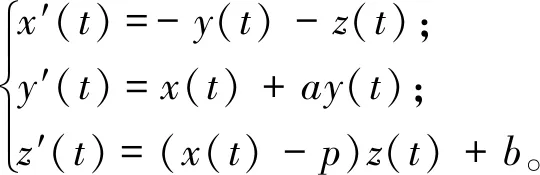
(1)

基于Rössler系统，本文研究的时滞Rössler系统可以描述为：

(2)

其中：x，y，z为变量；a，b，p为常量(a>0,b>0,p>0)；τ为时滞参量(τ>0)。

时滞Rössler系统的平衡点满足以下条件：

(3)

在平衡点E2处求得线性化系统(其余平衡点与此类似，故本文未做进一步分析)：

(4)

令p-x1=c，变换后的时滞Rössler系统为：

(5)

其对应的特征方程为：

λ3+cλ2+λ+c-(aλ2+acλ)e-λτ=0，

(6)

其中：λ为特征方程的根。

2 Hopf分岔分析

设当τ>0时，λ=iw(w>0)是式(6)的一个纯虚根，将其代入式(6)中可得：

-iw3-cw2+iw+c+(-aw2+iacw)(-coswτ+isinwτ)=0。

(7)

令实数和虚数分别等于0：

(8)

移项，同时平方可得：

w6+(c2-a2-2)w4+(1-2c2-a2c2)w2+c2=0。

(9)

命题1式(9)至少存在一个实根。

证明在式(9)中，令w2=x，则有：

x3+(c2-a2-2)x2+(1-2c2-a2c2)x+c2=0，

令

f(x)=x3+(c2-a2-2)x2+(1-2c2-a2c2)x+c2，

得到：

f(1)=-a2-a2c2<0，f(0)=c2>0。

根据零点存在定理,∃ζ∈(0,1)使得f(ζ)=0。因此，式(9)存在一个实根。证毕。

设w0为式(9)的一个实根，同时，根据式(8)可得：

(10)

将w=w0代入式(10)，得到时滞参量τ的值为：

(11)

其中：k=0,1,2,3，…。

因此，(w0,τk)是式(7)的解，即当τ=τk时，式(6)有共轭虚根λ=±iw0。

从而得到：

定理1设λ(τ)=m(τ)+in(τ)(其中，m(τ)和n(τ)均为τ的表达式)是式(6)的特征根，则有τ=τk使得m(τk)=0,n(τk)=w0。

证明对式(6)求导可得：

(12)

根据式(6)可得：

λ3+cλ2+λ+c=(aλ2+acλ)e-λτ。

(13)

将式(13)代入式(12)，可得：

(14)

根据式(14)和定理1可得：

(15)

由式(6)可得：

(16)

移项得：

(17)

化简式(17)，可得：

(18)

将式(18)代入式(15)，可得：

(19)

又

(20)

将式(20)代入式(19)，可得：

(21)

即：

(22)

(Ⅰ)若τ∈(0,τ0)，系统在平衡点E2处由不稳定逐渐变为稳定。

(Ⅱ)若τ=τk(k=0,1,2,…)，系统在平衡点E2处发生Hopf分岔，同时产生极限环。

(Ⅲ)若τ>τ0，系统在平衡点E2处是不稳定的，但在一定范围内极限环依然存在。

以上结论表明:系统在τ=τk时,发生了超临界Hopf分岔[22]。

3 数值仿真

3.1 数值分析

依据结论(Ⅰ)～结论(Ⅲ)，令a=b=0.2,p=5.7，则时滞Rössler系统变为：

(23)

依据结论(Ⅰ)～结论(Ⅲ)，得到：

下面运用MATLAB软件证明上述结论。

3.2 仿真结果

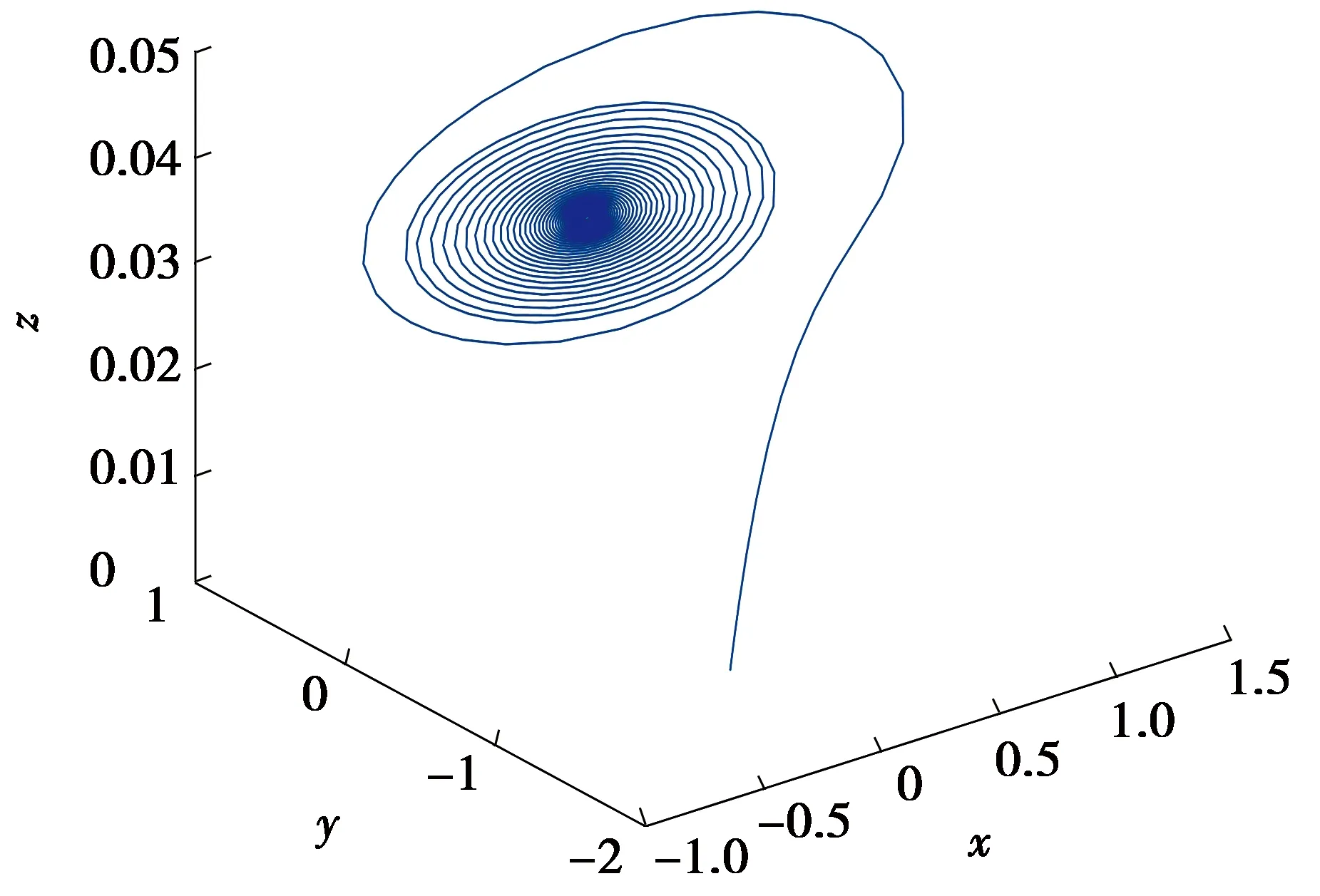
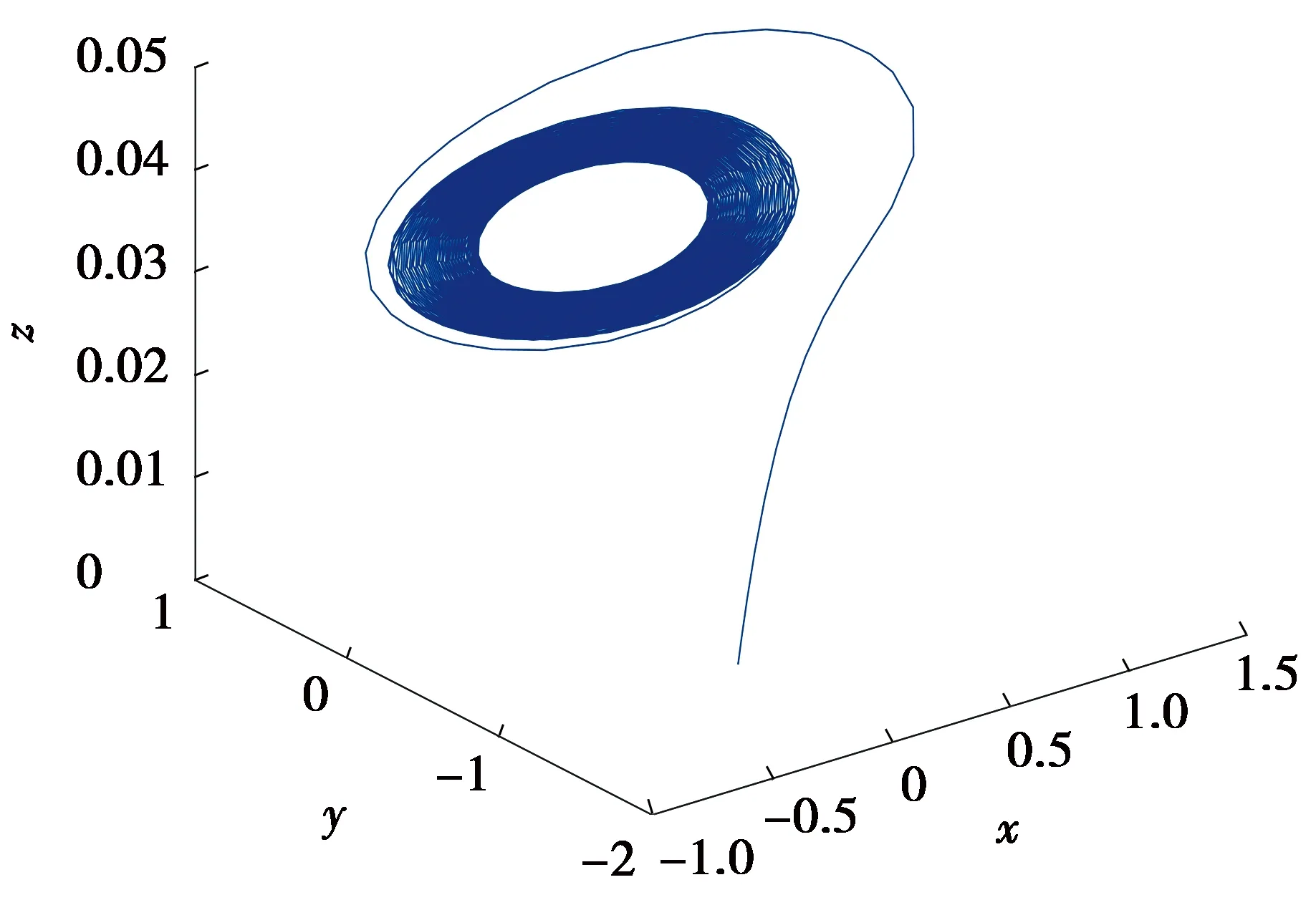
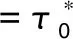
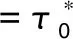
3.2.4 变量z在一定时滞范围内的Hopf分岔

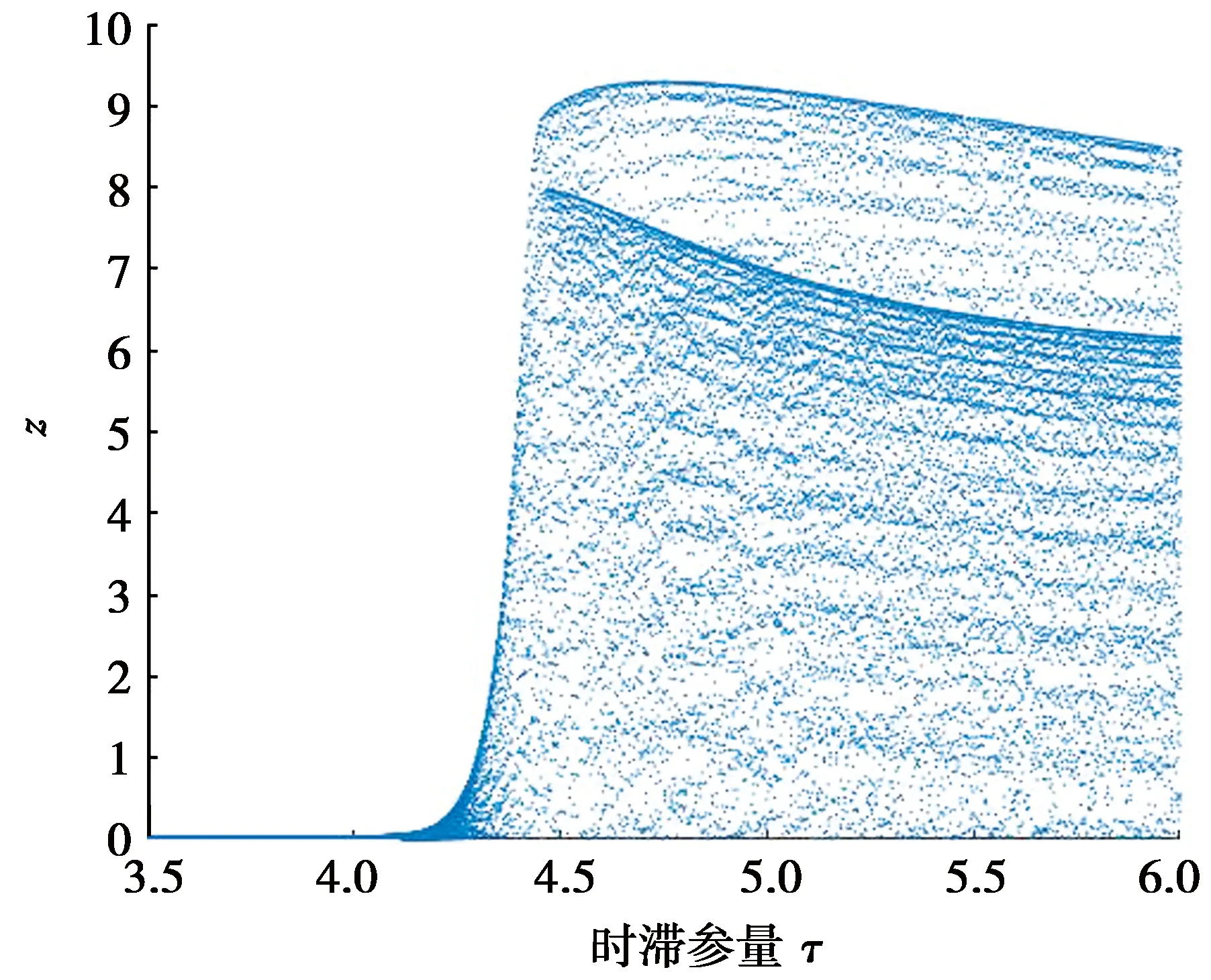
图7 时滞参量τ∈(3.5,6.0)

图8 时滞参量τ∈(3,11)

4 结束语

本文研究了时滞Rössler系统的Hopf分岔问题，得到如下结论：时滞Rössler系统中的时滞参量τ从τk增大到τk+1的过程中，系统由混沌逐渐变为稳定，且当τ=τk时系统发生Hopf分岔并形成极限环，当τ超过τk一定范围时，极限环消失，系统发生混沌现象。通过MATLAB软件仿真，给出了不同时滞参量条件下系统的三维空间相图和时间序列，并以变量z为例，给出了其在一定时滞范围内的Hopf分岔图，证明了所述结论的正确性。本文使Rössler混沌系统的理论更加完备，使得Rössler系统在混沌同步和保密通信等领域有了更为广阔的发展前景，并为Rössler系统在工程实际中的应用提供了更加丰富的理论依据。