袁修开,孔冲冲,顾 健

(厦门大学 航空航天学院， 福建 厦门 361005)

在结构可靠性分析中，失效概率的求解方法可分为三类：近似解析法、数字模拟法、代理模型方法[1]。近似解析方法包括改进一次二阶矩(Advanced First Order Second Moment, AFOSM)[1-2]、均值一次二阶矩(Mean Value First Order Second Moment, MVFOSM)和R-F法[3]等。近似解析方法计算量少，但是在处理复杂非线性问题时，其精度难以保证。数值模拟法包括蒙特卡洛仿真(Monte Carlo Simulation， MCS)[4]、线抽样(Line Sampling, LS)[5-6]法、重要抽样(Importance Sampling, IS)[7]和子集模拟(Subset Simulation, SS)[8-9]等。该类方法为了保证计算精度，需调用结构功能函数的计算次数较多，计算代价大，且在处理包含有限元模型的隐式极限状态问题时，计算效率低下，是影响该类方法应用的重要因素。代理模型方法包括响应面法[7-11]、神经网络法[12-13]、支持向量机法(Support Vector Machine, SVM)[14-16]等。该类方法专门针对隐式极限状态问题，能够显著提高分析效率，因而在工程中得到广泛应用，其中Kriging方法作为一种典型的连续插值迭代方法，以其精确的插值技术备受人们的关注[17]。本文着眼于采用该技术来进一步提高改进一次二阶矩方法的分析效率和适用范围。

改进一次二阶矩法通过将非线性功能函数线性展开，然后用线性功能函数的失效概率来近似原非线性功能函数的失效概率[1]。和均值一次二阶矩法相比，AFOSM在设计点(Most Probable Point, MPP)处而非均值点处将功能函数线性化，提高了分析计算的精度。吕震宙等[1]对改进一次二阶矩的理论介绍和推导过程做了详细的描述。改进一次二阶矩亦在众多工程领域得到了广泛的应用，比如：葛耀君等[18]在桥梁颤振可靠性评估中，使用改进一次二阶矩方法计算了小失效概率条件下的可靠度；侯晓亮等[19]在评价软土基坑支护设计中的抗隆起稳定性时，采用改进的一次二阶矩可靠度计算方法评价基坑抗隆起稳定性；郑财等[20]在研究三轴数控机床的运行误差时，用改进一次二阶矩法对其可靠性及灵敏度进行了分析计算；曾照辉等[21]在研究动力涡轮工作时的可靠性时，采用参数化建模通过混合模拟(有限元、响应面、改进一次二阶矩法三者结合)的方法对其进行可靠性分析等。改进一次二阶矩针对变量维数小，非线性程度不大的小失效概率问题来说，具有很高的计算效率和良好的分析效果。然而在改进一次二阶矩中求解“设计点”，及其包含的偏导数的计算是难点，目前常用的方法为有限差分法，但是其对于隐式极限状态函数(需有限元分析)，有限差分的步长很难确定，且增加了功能函数的计算次数，增大了计算量、效率低。

Kriging代理模型不仅具有良好的拟合效果和局部估计的特点，而且具有较好的连续性和可导性，故具有广泛的应用前景。韩忠华[22]在Kriging模型及代理优化算法研究进展中，对Kriging方法的背景、意义、理论以及发展现状做了详细的描述；聂雪媛等[23]在研究飞行器结构刚度气动优化设计中采用Kriging方法建立代理模型，该方法能够处理复杂目标的全局优化问题；黄晓旭等[24]提出一种将Kriging模型与子集模拟方法结合的可靠性分析方法用于解决小失效概率的工程结构问题；陈立立等[25]采用Kriging代理模型进一步验证自由变形技术在RAE2822翼型优化设计中的应用；韩少强等[26]提出了一种将梯度信息与Kriging模型构建相结合的方法用于气动反设计研究。

基于改进一次二阶矩的实用性及Kriging模型的效率和良好的可导性，本文提出一种Kriging与改进一次二阶矩融合的可靠性分析方法。所提方法在改进一次二阶矩迭代计算设计点的过程中借助Kriging模型计算迭代点的偏导数值，并将迭代过程中的迭代点用于更新Kriging模型，两者有机融合来求解失效概率。最后通过结合数值算例与工程算例验证该方法的可行性和高效性。

1 Kriging方法

(1)

其中：F(β,x)为线性回归模型；z(x)为一随机过程；f(x)=[f1(x),f2(x),…,fp(x)]Τ(p为基函数的数目)为输入向量x的多项式基函数，提供模拟的全局近似[29]；β=[β1,β2,…,βp]Τ为回归系数列向量。

函数z(x)为高斯随机过程[30]，作为局部近似[29]，其均值为0，方差为σ2，协方差满足下式的特征：

Cov[z(x(i)),z(x(j))]=σ2R(γ,x(i),x(j))

(2)

式中：γ=[γ1,γ2,…,γn]为一个相关函数中参数向量；x(i),x(j)是试验样本X中任意两个样本点；R(γ,x(i),x(j))为相关函数，相应类型有高斯函数、指数函数、幂函数、样条函数等[31-33]。这里采用常用的高斯相关函数，其数学表达式为：

(3)

当获得样本输入X={x(1),…,x(N0)}(N0为初始样本量)和输出Y={y(1),…,y(N0)}后,可以计算得到式(1)中的回归系数向量β*和式(2)中过程方差σ2[32]：

β*=(FTR-1F)FΤR-1Y

(4)

(5)

相关函数中的参数向量可以通过极大似然估计得到：

(6)

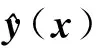
(7)

式中，r(x)=[R(γ,x(1),x),…,R(γ,x(N0),x)]T为输入量x与已知样本点X的相关函数，r*可以通过计算Rr*=Y-Fβ*得到。对于Kriging模型的详细理论分析可以参照文献[32-33]。

Kriging模型对输入量和响应量的关系可达到较高的拟合精度，且在工程中已经得到了广泛的应用[23-26]。

2 基于Kriging方法与改进一次二阶矩的融合方法

所提方法采用Kriging方法高效计算偏导数，用于进一步提高改进一次二阶矩的效率。由于Kriging模型中的回归函数和相关函数都是简单的函数体，在模型建立好后，即可简便计算出相应的偏导数，因此可将之用于改进一次二阶矩的求解过程中。同时，由于一般情况下样本量越多，Kriging模型构建越精确。为了充分利用已有信息，所提方法将改进一次二阶矩求解进程中的近似设计点信息运用于Kriging模型的更新构建中，提高Kriging模型的精度，进而将Kriging方法与改进一次二阶矩有机融合。

步骤1：构建Kriging模型。

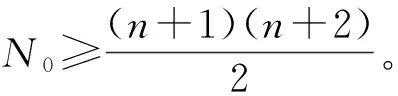
采用蒙特卡洛法随机抽取N0样本点X={x(1),x(2),…,x(N0)}(含均值点)，代入结构功能函数中计算响应值Y={y(1),…,y(N0)}，然后根据样本点构建初始的Kriging模型。

当回归模型采用一阶多项式，则输入向量x的基函数向量为f(x)=[1,x]，随机过程采用高斯过程，如式(3)所示，由第1节式(4)可知样本量、回归模型、随机过程确定后，便得到回归系数向量β*和r*，于是得到极限状态函数g(x)初始的Kriging代理模型

(8)

步骤2：将Kriging导数信息运用于AFOSM。

在原有改进一次二阶矩方法中，对原极限状态函数在设计点x*处线性化：

(9)

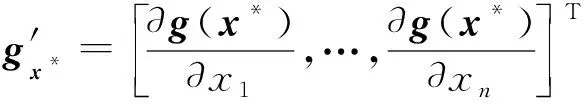
一般采用迭代的算法来获得[1]设计点，即设置初始设计点值，如设为均值点x*(0)=μ，而后在迭代过程中逐步对设计点值进行更新。此外，在计算导数的时候，需要较多的计算代价，尤其是在变量维数较多的情形下。在本文所提方法中，采用构建的Kriging代理模型来获取近似导数信息，进一步提升AFOSM的效率。即运用式(8)所示的代理模型计算导数

(10)

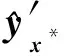
(11)

由此，在后续改进一次二阶的迭代求解过程中，导数的计算完全由构建的Kriging模型来计算。

步骤3：更新Kriging模型及设计点直至收敛。

将迭代过程中的中间迭代点添加到构建初始Kriging代理模型的样本点中，对前面建立的Kriging代理模型进行更新和修正，提高Kriging模型的精度，从而提供更为准确的导数信息，为所提融合方法的最终收敛提供保障。做法如下：

重复将步骤2中得到的设计点值应用到步骤1中，更新Kriging模型的迭代过程，直到前后两次的可靠度指标的相对误差满足设定的精度要求为止，最后对应的可靠度指标ψ和失效概率Pf为：

(12)

Pf=Φ(-ψ)

(13)

本文所提方法的流程图如图1所示。

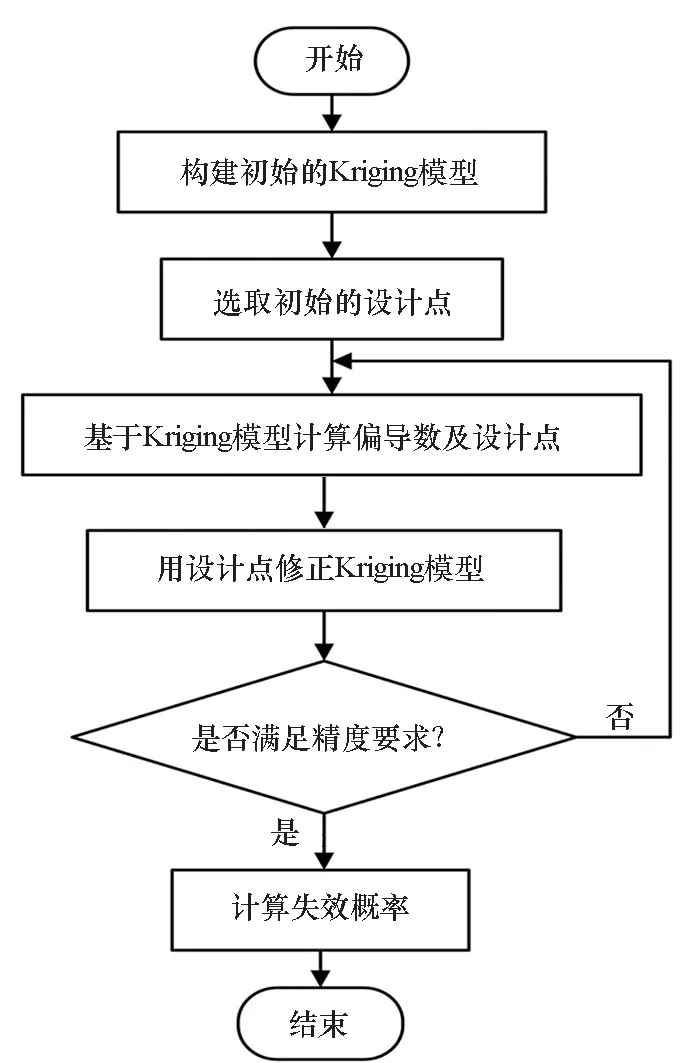
图1 Kriging与改进一次二阶矩融合方法流程图Fig.1 Flow chart of Kriging and AFOSM

3 算例分析

为了验证所提方法的适用性，该节结合数值算例和屏蔽闸阀结构的工程算例进行说明。采用本文所提融合方法对各例进行可靠性分析，并与其他分析方法进行比较，包括：AFOSM，即常规改进一次二阶矩方法[1]；Kriging+MCS，即建立足够精度的Kriging模型后再使用MCS方法[28]；MCS，即直接使用蒙特卡洛法。

本文以MCS直接方法计算的值作为精确值(通过大样本数来计算得到)，以AFOSM 和Kriging+MCS两种方法来与本文方法进行对比。需要指出的是，对于可靠性计算效率的评定，一般通过极限状态的计算(调用)次数来衡量。本文构建Kriging模型所采用的样本点是通过计算极限状态函数得到，所以样本点数也表示了极限状态函数的计算次数。为了考察本文所提方法中初始Kriging模型构建的随机性，采用不同数目的样本点构建初始Kriging模型，然后进行可靠性分析。在以下三个算例中用本文方法1和本文方法2表示不同样本点下本文所提方法计算效果。

算例1非线性极限状态函数g1(x)为：

g1(x)=x1-x2x3

(14)

其中：变量x1,x2,x3均服从正态分布，其分布信息分别为x1～N(7000,14002)，x2～N(187 500,28 1252)，x3～N(0.024,0.001 442)。

首先验证用Kriging方法计算改进一次二阶矩偏导数的可行性。本文方法采用蒙特卡洛随机抽取5个样本点和均值点组成的初始样本点构建初始Kriging模型，由构建的Kriging模型计算第一次迭代点即均值处偏导数信息，同时使用AFOSM中有限差分(其步长为0.001)计算偏导数，以下算例与此相同，计算结果如表1所示。

从表1可以看出，在均值点处，根据初始Kriging方法得到的偏导数与理论计算出来的偏导数的相对误差在3%以内，已具有足够的精度。

采用本文方法及其他方法进行可靠性分析的结果如表2所示。以MCS方法的结果(视作精确值)作为参照，各方法的失效概率与精确值都比较接近，误差均小于1%。从计算效率上讲，AFOSM计算极限状态函数26次，Kriging+MCS方法中使用200个样本点构建了Kriging代理模型，而后用蒙特卡洛抽样方法计算失效概率。本文方法收敛准则为|ψi-ψi+1|/ψi≤5%，以下两个算例中设计点的确定方法相同。本文方法1使用6个初始样本点构建初始Kriging模型，经过两次迭代修正便可计算出极限状态函数的失效概率，计算次数为6+2。为了检验方法稳健性，使用不同的初始样本点进行分析，亦列在表中，记为本文方法2，计算次数为4+2。表2中本文方法1和本文方法2计算结果一致，与MCS计算结果在误差允许范围内，由此可以看出本文所提方法的效率和适用性。

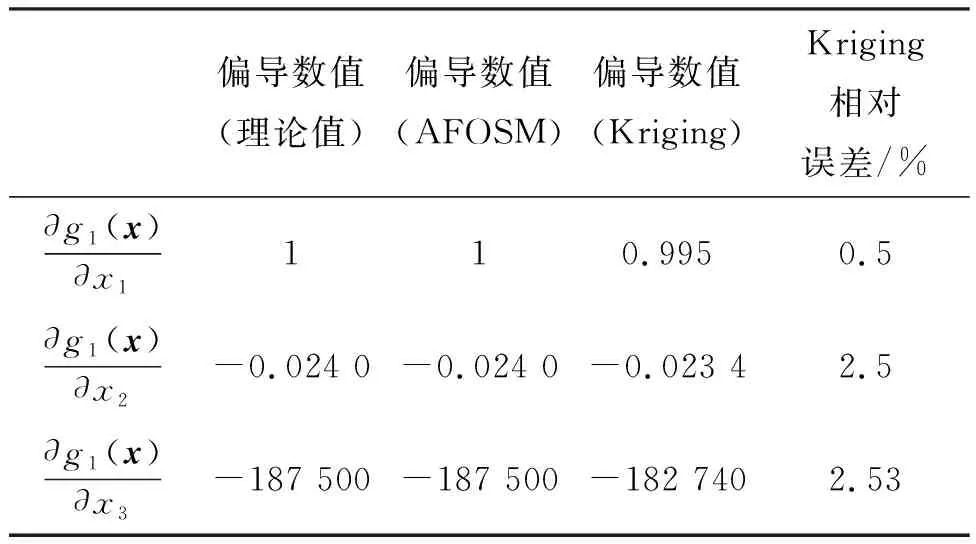
表1 初始Kriging模型计算极限状态函数的偏导数(均值点)Tab.1 Partial derivative of the limit state function by the initial Kriging model (at the mean point)

注：∂g1/∂xi为极限状态函数对变量的偏导数值。

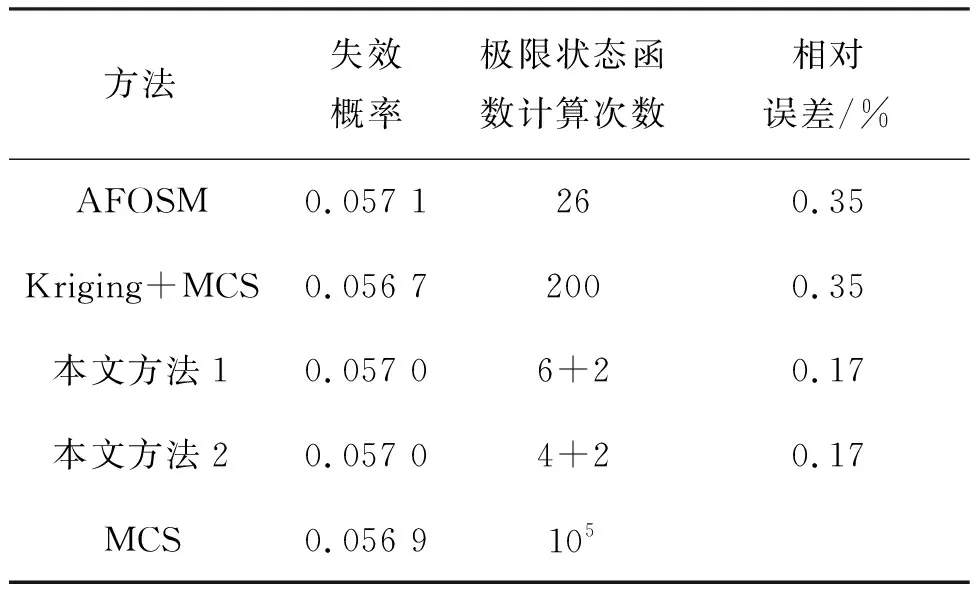
表2 算例1不同方法得到的可靠性分析结果Tab.2 Reliability analysis results obtained by different methods in example 1

算例2非线性极限状态函数g2(x)为：

(15)

其中：基本随机变量x1,x2,x3,x4均服从正态分布，分别为x1～N(83.5,0.122)，x2～N(83.5,0.122)，x3～N(83.5,0.122)，x4～N(150,0.252)。

采用本文融合方法计算均值点处的偏导数值如表3所示，可靠性分析结果如表4所示。

从表3可以看出，在均值点处，根据初始Kriging方法得到的偏导数与理论计算出来的偏导数值相对误差在7%以内，与算例1相比相对误差值偏大，原因是极限状态函数的非线性提高，随机变量的维度增多。

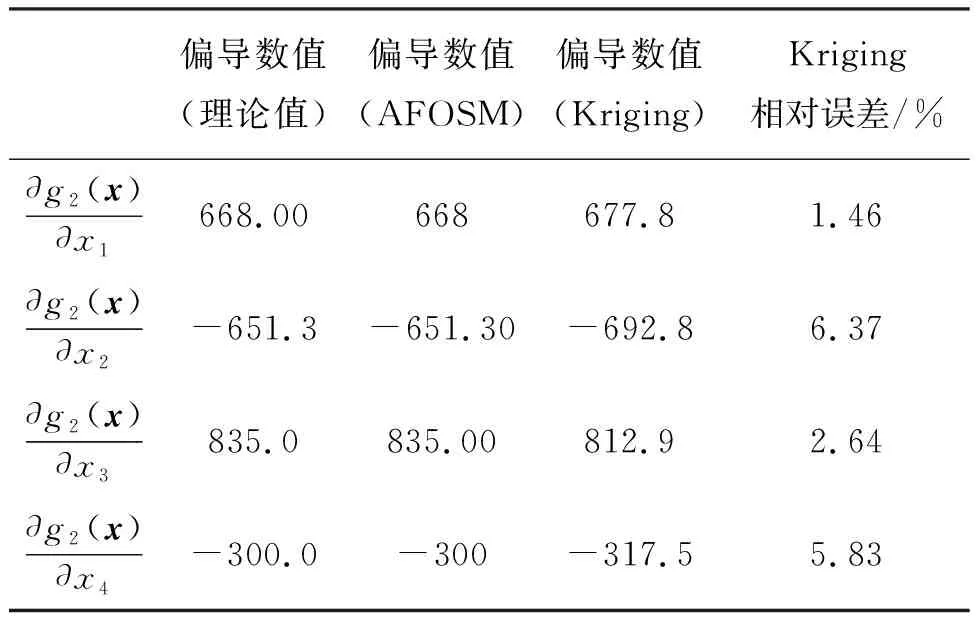
表3 基于初始Kriging模型计算极限状态函数的偏导数(均值点)Tab.3 Partial derivative of the limit state function by the initial Kriging model (at the mean point)

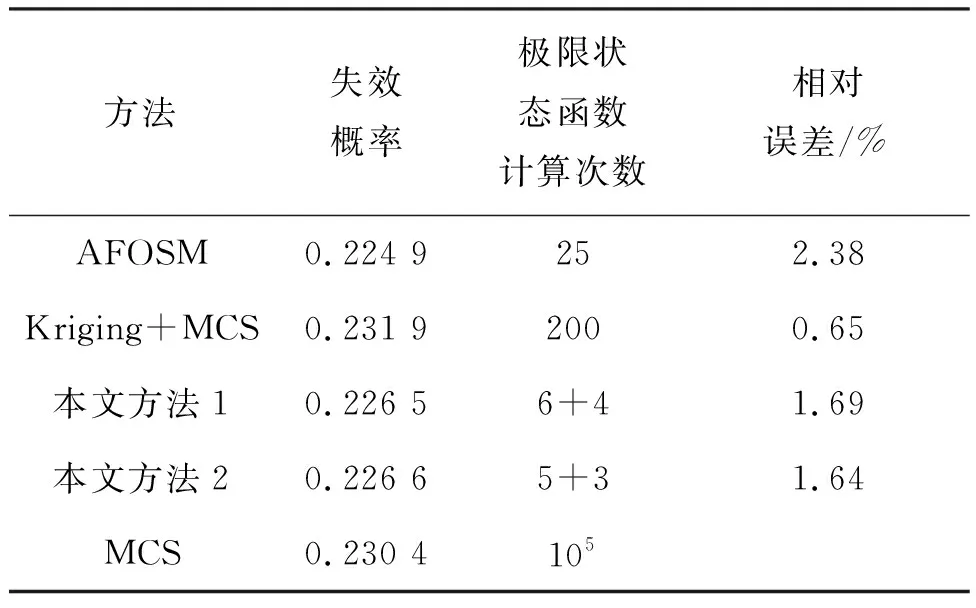
表4 算例2不同方法得到的可靠性分析结果Tab.4 Reliability analysis results obtained by different methods in example 2

同样从表4可以看出，以MCS方法的结果(视作精确值)作为参照，其他三种方法的失效概率与精确值都比较接近，但是从计算极限状态函数的次数来说，对于常规改进一次二阶矩调用次数最多为25次，Kriging+MCS方法采用200个样本构建Kriging模型。而本文方法采用不同的初始样本数来进行分析，结果亦列在表中本文方法1和本文方法2。可以看出本文方法计算次数最少，效率最高。

算例3闸板可靠性分析一屏蔽闸阀的结构如图2所示，建立相应的有限元来分析接触面(闸板与密封座)最大应力值。该结构的相关参数有：闸板的倾斜角θ，材料弹性模型E，闸板与密封座的摩擦系数f，闸板上端的均布载荷p。假定各参数均服从正态分布，分布参数为θ～N(5，0.12)，p～N(140,102)，E～N(197 000,10002)，f～N(0.24,0.012)。以结构的最大应力不超过给定极限应力，建立结构的极限状态函数，即

g(θ,E,f,p)=[σ]-σmax

(16)

其中：[σ]=310 MPa为极限应力；σmax为结构中阀板和密封座接触面的最大应力值可以表达为：

σmax=ANSYS(θ,E,f,p)

(17)

其中，ANSYS(θ,E,f,p)表示由调用ANSYS有限元分析得到。

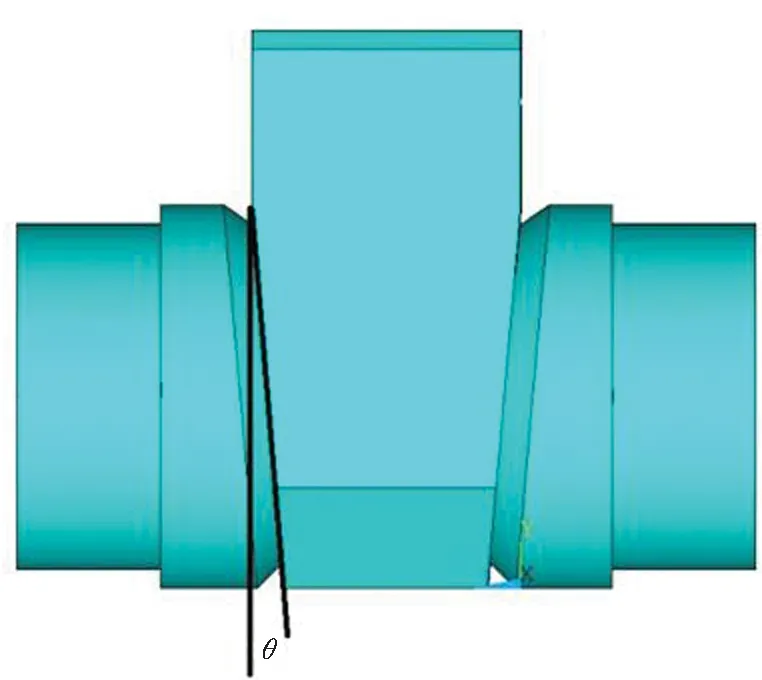
(a) 正视图(a) Front view

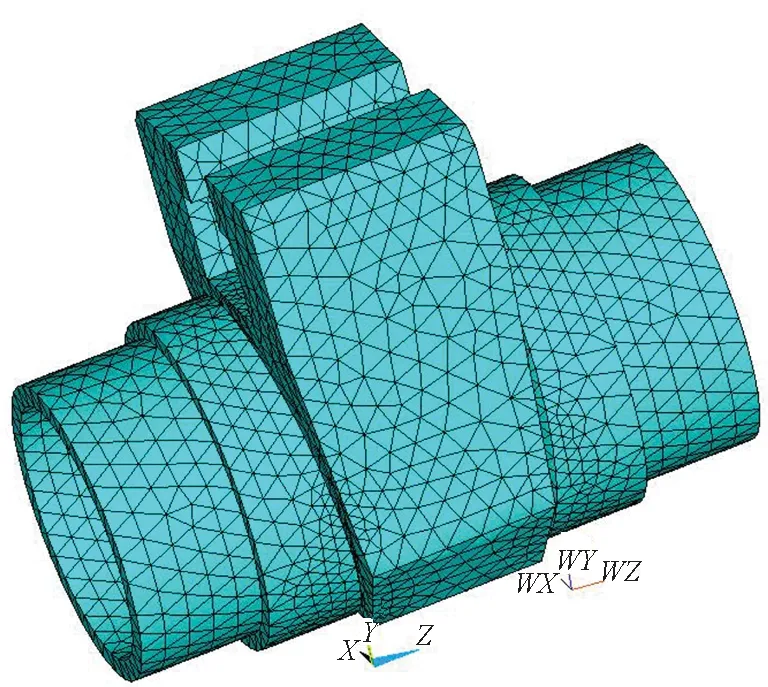
(b) 有限元网格划分(b) Finite element meshing图2 屏蔽闸阀结构的三维有限元模型Fig.2 The three-dimension finite element model of shielded gate valve structure

表5给出了各方法的计算结果。可以看出，对于隐式函数，常规的AFOSM方法无法计算结构的失效概率，从侧面也反映了本文所提方法的优势。Kriging+MCS使用300个样本点构建了Kriging代理模型，然后通过MCS计算失效概率。本文方法计算两次，一次调用6+6次结构极限状态函数，另一次调用5+4次，计算得到的失效概率值相近。同样从该例可看出本文所提方法的效率和对解决工程结构问题的适用性。

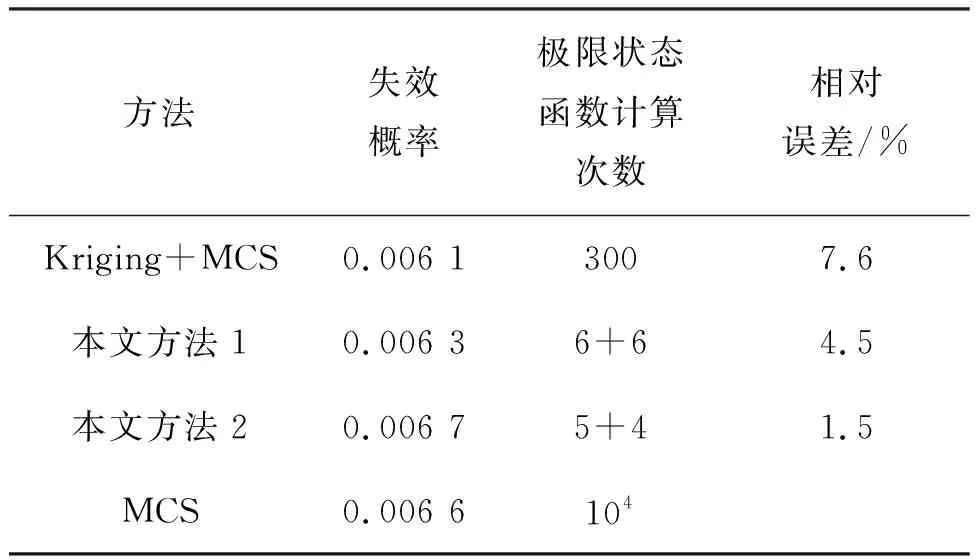
表5 屏蔽闸阀的可靠性分析结果Tab.5 Reliability analysis results of shielded gate valves

4 结论

本文提出了将Kriging方法和改进一次二阶相融合的可靠性分析方法。该方法针对AFOSM在处理复杂非线性函数或包含有限元分析的隐式极限状态函数的可靠性问题时，采用Kriging方法求解极限状态函数的偏导数，为AFSOM迭代计算设计点时提供偏导数信息，同时将AFSOM迭代产生的中间迭代点用于更新Kriging模型进一步提高偏导数的计算精度。

通过两个数值算例可以看出，所提方法中运用Kriging得到求解梯度信息与理论计算的基本一致。最终计算的结果亦能满足精度要求，而在效率上与传统的AFSOM相比有了进一步的提升。所提方法拓宽了AFOSM使用的范围，可以用于解决复杂的工程可靠性问题，且提高了其求解效率。