程泽鹏，邱思逸，向阳,*，邵纯，张淼，刘洪

1. 上海交通大学 航空航天学院，上海 200240 2. 中国商用飞机有限责任公司 上海飞机设计研究院，上海 201210

翼尖涡是由机翼上下表面压力差所产生，从机翼表面脱落后在飞机尾迹中形成的主要大尺度涡结构。翼尖涡的产生不可避免地带来尾迹遭遇[1]、诱导阻力[2]和气动噪声[3]等问题，对飞机的安全性、经济性和舒适性带来不利影响。为此，国际民航组织(ICAO)对两架飞机的起飞时间间隔和距离间隔做出严格的限定。以起飞重量超过136 000 kg的重型飞机为例，当后续飞机的起飞重量小于7 000 kg时，两者的间隔时间不得少于159 s，间隔距离不得低于6海里[2]。除此之外，飞机在巡航过程中，由翼尖涡导致的诱导阻力占比达到30%～40%[4]。为减轻翼尖涡的不利影响，2002年，Gerz等从翼尖涡本身物理特征出发总结出两大策略：① 降低翼尖涡的强度；② 加快翼尖涡的衰减[2]。在此基础上，James和Frank于2018年从翼尖涡不稳定特性的角度进一步将其总结为：① 通过改变展向载荷或通过自然激发的不稳定性实现涡/涡系的修正和衰减; ② 通过使用某种形式的主动控制来施加外部扰动加速翼尖涡的失稳衰减[5]。翼梢小翼作为一种有效的减阻手段，已经成为大型客机不可缺少的一部分。翼梢小翼不仅降低翼尖涡强度，同时改变翼尖涡结构，进而影响翼尖涡的不稳定性特征；但是针对小翼结构下的翼尖多涡系统的不稳定性特征及其演化机理认识十分有限，限制了对于小翼的进一步改进和优化。如何使得小翼不仅能减阻，而且能控制翼尖涡稳定性使其快速衰减失稳值得深入研究。

翼尖涡的不稳定特性主要表现为长波不稳定性、椭圆不稳定性和翼尖涡的摇摆现象，对于其各自的演化机理一直以来都是研究的重点和热点。翼尖涡的长波不稳定首先由Crow在分析等强度对转Rankin涡对的流动现象中发现并阐述[6]，主要由以下3种效应共同叠加导致：① 与涡核流体旋转方向相反的自诱导旋转；② 由另一个涡引起的拉伸作用；③ 两个涡的互诱导运动[7]。Leweke和Charles[8]的实验结果和Grégoire等[9]的数值结果进一步表明，长波不稳定性表现为涡对关于其中心平面对称的一种正弦变形，并与对称面呈45°倾斜，变形幅度会沿流向逐渐增大直到两个涡核最终接触并重叠；随后翼尖涡发生重新连接，在经历若干个周期后，最初的涡对转变成一系列三维涡环。短波不稳定性则源自于涡对中一个翼尖涡的两个扰动波(开尔文模态)与另一个涡对产生的应变场之间的共振机制，这种共振可以导致扰动波按照指数规律放大，从而引起涡旋的不稳定性。在较低的雷诺数(103～105)条件下，发生开尔文模态的共振条件为两个开尔文模态周向波数之差为2，Leweke和Charles[10]对无轴向流动的涡对运动分析结果表明，共振条件是扰动模态的周向波数为-1和1的组合；Roy等[11]验证了有轴向流动的涡对运动中，共振条件是扰动模态的周向波数为2和0的组合。而在更高雷诺数条件下，共振条件则要求两个开尔文模态周向波数之差为3[7]，并且在涡最终破碎耗散之前还会引起二次不稳定[12]和涡的重连[13]等更为复杂流动现象。翼尖涡的摇摆现象首先由Baker等在水槽实验中发现[14]。随后，Devenport等[15]的热线实验结果也证实翼尖涡摇摆现象的存在，分析结果表明翼尖涡摇摆幅值随流向位置而逐渐放大。Edstrand等[16]对体视粒子图像测速(SPIV)结果分析，发现由线性稳定性分析(LSA)获得的最不稳定模态结构与由本征正交分解(POD)获得的主模态结构一致，从而科学地说明翼尖涡摇摆运动来源于不稳定性。在此基础上，本文作者团队[17-18]研究表明在低湍流度情况下，摇摆幅值随不同工况(雷诺数、攻角)和流向位置的发展规律与由局部线性稳定性分析获得的不稳定放大因子(频率、波数)随不同工况和流向位置的变化规律具有一致性，从而更进一步地揭示翼尖涡摇摆现象的来源。

对翼尖涡的不稳定模态及其演化机理的研究有助于理解翼尖涡不稳定现象背后的物理本质，对于翼尖涡的科学控制原理有指导意义。相对于局部 LSA只能对近似轴对称的孤立翼尖涡进行线性稳定性分析, 全局线性稳定性分析(Bi-global LSA)能对双涡及双涡以上、涡与尾迹的相互作用等复杂流动现象予以分析。Moored等[19]对桨叶施加与用Bi-global LSA得到卡门涡街的最大空间生长率相对应的驱动频率时，获得最优的推进效率。当卡门涡街的不稳定模态发生转捩时，对应的尾迹结构会从一种结构变成另一种结构形式[20]。这些结果对基于翼尖涡不稳定模态的控制思路具有很好的启发意义。此外，理论分析表明，孤立Lamb-Oseen涡[21]/涡对[22]、Batchelor涡[23]均对周围环境存在一个最不稳定的扰动。在最不稳定扰动的作用下，孤立涡获得的扰动增益可达到102～103；涡对获得的扰动增益可达到104。在准定常演化阶段，以观察者的视角和涡的视角，扰动能量均会逐渐增强；此外，雷诺数越大，翼尖涡不稳定模态的扰动能量也会增加[21,24]。然而，这些研究都是理论涡模型，较难真实反映实际翼尖涡的流动不稳定性。最近，Edstrand等[25]在Re=1 000下，针对NACA0012等直机翼产生的翼尖涡及其尾迹进行时间和空间的全局稳定性分析，结果表明带尾迹的孤立涡特征值在时间和空间上存在尾迹分支、涡主分支和连续分支；在空间上还包含涡次级分支。尾迹分支则主导流动中最主要的不稳定特性。进一步地，按照尾迹分支中的不稳定频率施加外部扰动时，发现按照第五阶模态施加的体积力会使翼尖涡获得最优的衰减[26]，从而提供低雷诺数下孤立翼尖涡的不稳定控制解决方案。然而，较高雷诺数下翼尖双涡系统的不稳定模态和演化机理的研究，仍然是一个新的课题。

为此，本文采用SPIV方法对加装双叉弯刀小翼的M6机翼在不同攻角、不同雷诺数，16倍尾迹区范围内的翼尖涡流场展开测量。采用Bi-global LSA来分析求解翼尖双涡结构的不稳定放大率和模态，在此基础上得到双翼尖涡结构在不同扰动波数和不同工况下的不稳定模态的演化机理，从而为加快翼尖涡的失稳衰减科学原理探讨和提出工程解决方案并提供参考。

1 试验搭建与数据处理

1.1 试验模型

试验中使用的模型为加装双叉弯刀小翼的M6机翼。如图1所示，后掠机翼翼根弦长为0.143 m，根梢比为0.56，展弦比为3.8，其他参数参照M6机翼。上、下小翼参照Whitcomb小翼构型设计，两者倾斜角均为60°，前缘后掠角分别为38°、52°。后掠翼和小翼连接处均保持光滑连接，以避免拐角处产生不必要的涡结构。

图1 机翼模型外形几何参数Fig.1 Geometric parameters of examined model

1.2 SPIV测量

本试验在上海交通大学低速回流式风洞中进行,该风洞的试验段截面为1.2 m×0.9 m的矩形，经过热线标定测得来流湍流度在0.3%以下。试验时，机翼安装攻角α为6°、8°和10°；来流速度u∞为15 m/s、30 m/s和45 m/s，对应的基于翼尖弦长(c=0.08 m)的雷诺数为Rec=0.82×105，1.64×105,2.46×105。相对于后掠翼的尾缘，在16倍尾迹区范围内等距离测量x/c=2，4，…，16共8个截面。试验过程中机翼的安装示意图如图2 所示，其中来流方向为x轴正方向，机翼上表面方向为y轴正方向，垂直于风洞壁面向上的方向为z轴正方向。由机翼和小翼造成的风洞阻塞度小于1%。

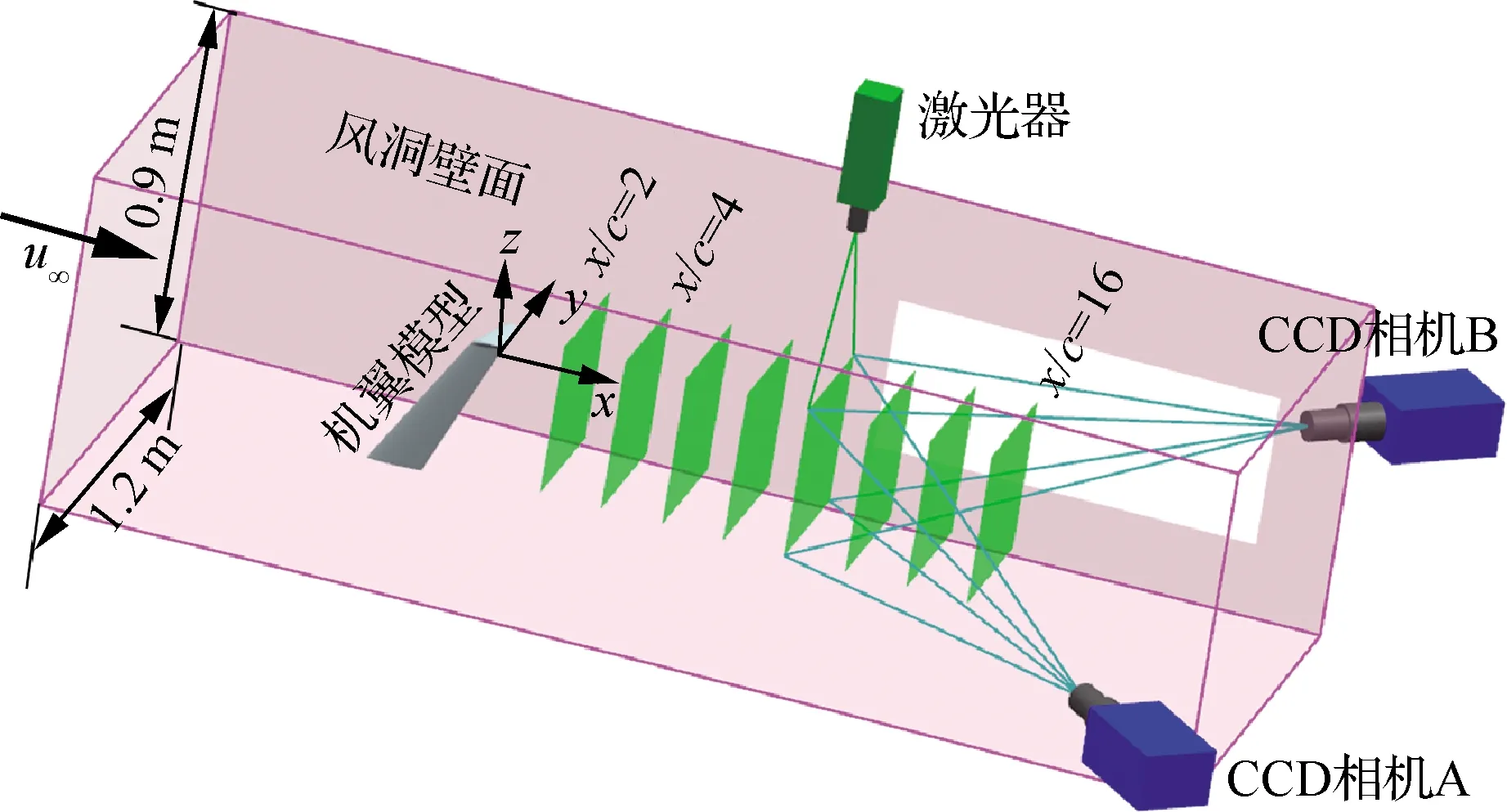
图2 SPIV试验示意图Fig.2 Schematic diagram of SPIV test

试验过程中，示踪粒子采用1～5 μm直径的雾化乙二醇油滴，保证良好的粒子跟随性。采用Nd:YAG双脉冲激光发射器发射波长为532 nm、脉冲能量为380 mJ的激光照亮测量区域。双脉冲发射频率为1 Hz，激光厚度为1 mm并垂直于来流方向。根据SPIV的测量精度对粒子在两帧图像时间内的位移要求，在15 m/s、30 m/s和45 m/s的来流条件下，两束激光的时间间隔分别设为Δt=15，7.5，5μs。试验拍摄的相机为Imager-Pco的高分辨率CCD相机，相机与激光器同步，发射与采样周期设置为1 s。为保证相机在x/c=16截面处的拍摄窗口足够，两个相机的安装角度保持在45°。相机采集的图像画幅为2 048像素×2 048 像素，拍摄画幅大小为292 mm×269 mm，对应的空间分辨率为0.131 mm/像素。每个工况下，左右相机均保存200幅瞬时图像，以求解时均流场信息并研究翼尖涡的摇摆特征。

采用TSI INSIGHT 4G软件对图像进行互相关计算。通过两次查询窗口确定粒子位移以提高速度矢量分辨率，初始查询窗口为72像素×72像素，有效重叠率为25%；第2次查询窗口为36像素×36像素，有效重叠率为50%，并通过9像素×9像素的填充算法由周围矢量插值出未能解算的速度矢量，后处理得到的达标矢量占总矢量的85%以上。由此产生的整个测量平面区域速度的测量误差小于1%[17]，满足试验结果的分析要求。

1.3 翼尖涡相关物理量的计算

在试验后处理中，瞬时流场和时均流场中翼尖涡的涡核位置均采用涡量质心公式的方法确定。以瞬时流场的计算为例，涡心位置(yc(t),zc(t))的计算式为

(1)

式中：ωx(y,z,t)为瞬时涡量；为去除试验中噪点对结果的影响，考虑置信范围，积分区域S1为集中最大涡量绝对值95%以上的涡量区域，即

|ωx(y,z,t)|≥0.05|ωx(y,z,t)|max

(2)

时均流场中的涡核半径采用与涡心位置类似的方式确定：

(3)

式中：yc、zc为时均流场中的涡心坐标；ωx(y,z)为时均流场中的流向涡量；积分区域S2的定义与S1类似。

2 全局线性稳定性分析方法

2.1 扰动方程

本试验中产生翼尖双涡结构，流场已不满足轴对称条件，但是在流向方向上可认为近似满足准平行流假设。此时，需采用Bi-global LSA对翼尖双涡结构展开稳定性分析。采用图2笛卡尔坐标系(x,y,z)下的不可压缩Navier-Stokes方程，流场中速度和压力等流动变量可表示为

(4)

忽略流向变化，基于傅里叶分解思想以线性小扰动表示的脉动矢量可写为

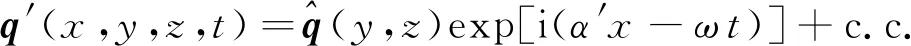
(5)

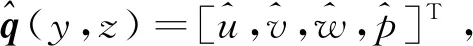
将流场变量代入不可压Navier-Stokes方程中，消去定常流动方程并略去高阶小量，得到Bi-global LSA的小扰动控制方程为

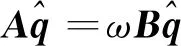
(6)

式中：A、B为稳定性矩阵，分别为

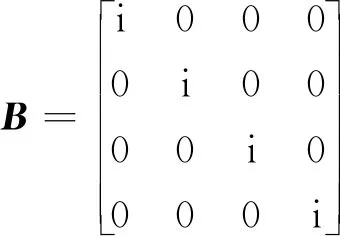
(7)

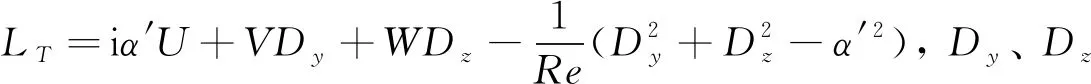
考虑到数值精度和收敛速度的要求，方程(6)的离散采用切比雪夫谱配置法[17，26]，对应的边界条件信息可参见文献[17]。通过求解方程(6)可得到特征值谱(ωr,ωi)和对应的特征向量。特征值中，ωi为翼尖涡流动在时间上最不稳定扰动模态对应的放大率。按照式(5)的结果可知，当ωi>0时，扰动在时间上会以指数形式衰减，即流动是不稳定的,而特征向量即为所期望得到的扰动模态信息。

2.2 程序验证

在对本文的翼尖双涡流场展开Bi-global LSA之前，先采用槽道流、孤立翼尖涡、等强度对转涡对、等强度同转涡对4个典型算例对程序予以严格的验证。在验证过程中，与文献结果保持一致，切比雪夫谱配置点的数目均为64×64。

在槽道流动验证计算中，设置条件与Theofilis等[27]的算例一致，宽高比分别为A=1，4。图3 为两者特征值谱的比较结果,可以发现，对于两种宽高比，特征值谱均符合完好。

图4(a)和图4(b)分别为孤立Batchelor涡和对转涡对[28]的全局时间稳定性验证结果，其中Batchelor涡的旋拧度q=0.475,Re=100，方位波数m=-1，流向波数α′=0.418。可以看出，无论是孤立涡，还是对转涡对，两种方法所得到的特征值谱基本吻合。特别地，对于ωi>0半平面上的不稳定特征值可以实现精准捕捉。

图3 槽道流结果验证Fig.3 Validation of cavity flow results

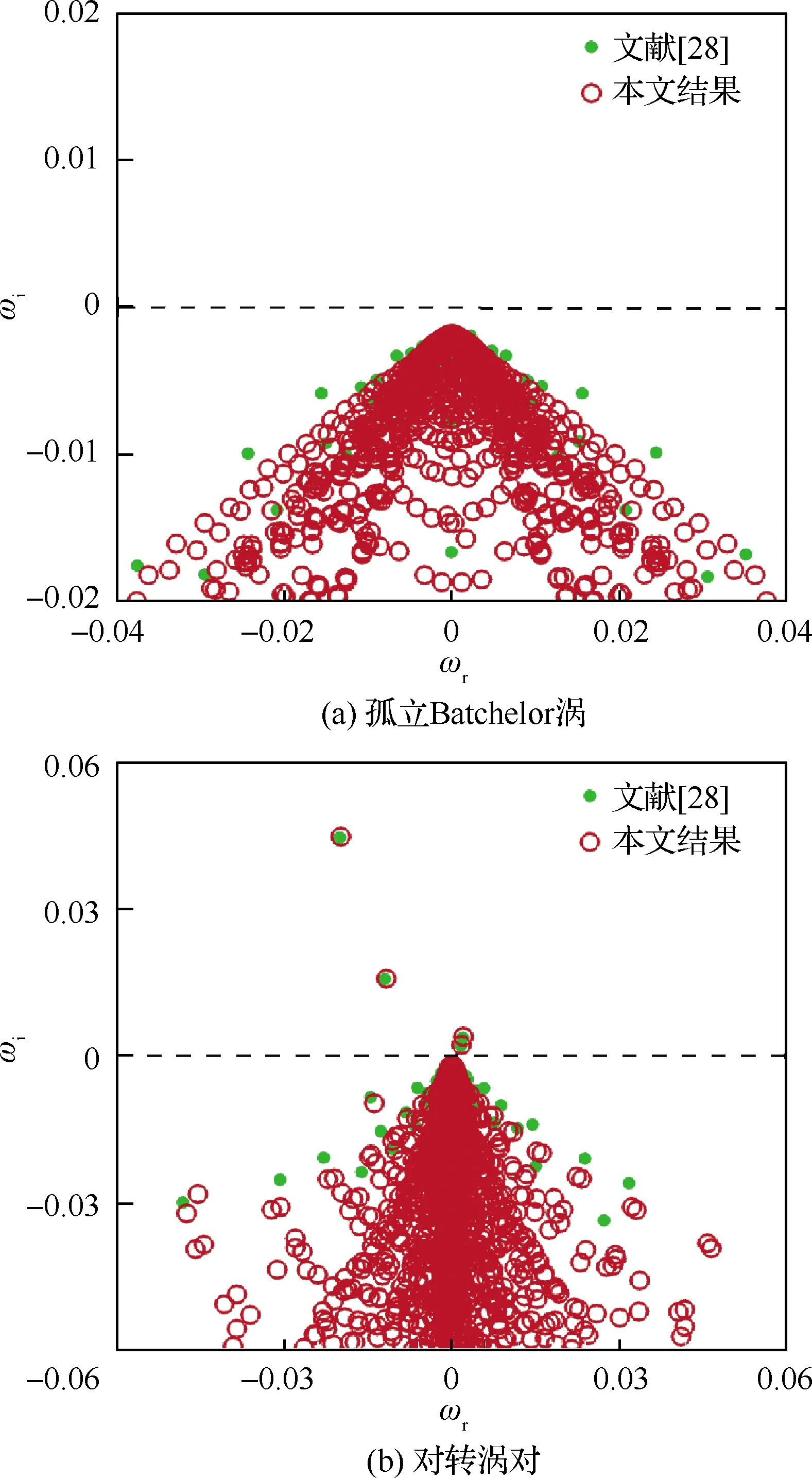
图4 孤立Batchelor涡和对转涡对的结果验证Fig.4 Validation of isolated Batchelor vortex and counter rotating vortex pairs results

在类似的参数条件下，Mayer和Powell[29]也曾做过孤立Batchelor的计算，表1列出本研究中得到的最不稳定特征值与Mayer和Powell的结果。可以看出，本研究计算得到的最不稳定特征值与文献[29]保持一致。

表1 孤立Batchelor涡流的结果验证Table 1 Validation of isolated Batchelor vortex flow results

为验证程序获取的扰动模态的准确性，程序还选取同转涡对作为验证算例。计算时初始流场为两个线性叠加的高斯涡，其初始涡核半径均为a=0.010 408 m, 涡心间距b=0.074 336 m，两涡的环量Γ1=Γ2=0.204 5 m2/s。

由于线性叠加的涡对并不是Navier-Stokes方程的解，以此为初始条件做无黏计算，在经过一个快速的松弛过程后，选取此时的流场作为全局时间稳定性分析的基准流动。此时a=0.011 2 m,Γ1=Γ2=0.204 3 m2/s，b=0.074 06 m，由此得到基于环量的雷诺数Re=13 989,a/b=0.15，流向速度为0 m/s。计算时流向波数与Roy等[11]的设置保持一致，取α′=2.0。在得到的特征谱中选取不稳定点，可以求解得到扰动模态，其结果与Roy等的结果对比如图5所示,可以发现，本程序对同转涡对中的扰动模态可以实现准确的捕获。

以上计算结果表明本文采用的方法对不稳定特征值谱和扰动模态均可以进行精确的捕捉，能够满足试验中得到的翼尖双涡结构流场的全局稳定性分析要求。

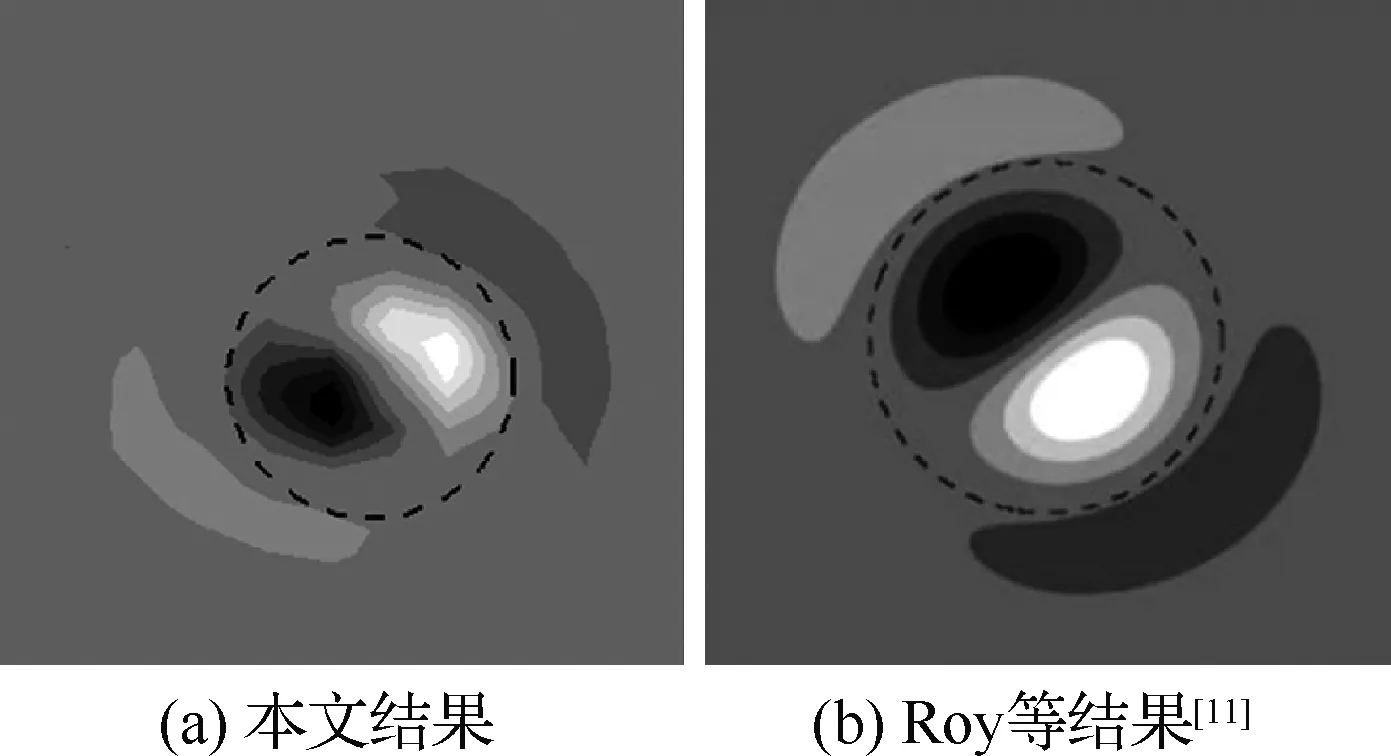
图5 同转涡对的扰动模态结果验证Fig.5 Validation of co-rotating vortex pairs flow results

2.3 翼尖双涡结构的Bi-global LSA 方法

进行全局线性稳定性分析时，关键之一是基本解的获取。在基于SPIV得到时均流场后，获取基本解之前还需进行以下步骤：① 对分析截面上的每个翼尖涡周向平均，获取旋向速度；② 对翼尖涡采用Lamb-Oseen涡模型拟合，并线性叠加；③ 在数值计算平台上对线性叠加涡对松弛计算[11,30-31]，使其满足Navier-Stokes方程的解；④ 以 流向涡量重构出轴向速度[11, 32]，从而获得最终的基本解。

本研究中，为尽可能消除尾迹对涡不稳定性潜在的影响，选取x/c=16截面处的时均流场作为分析截面。此外，根据已有结果，该风洞品质下，涡摇摆对速度场的影响十分有限[17]，因此分析流场没有考虑涡核对齐后的平均流场。松弛处理过程在商业软件Fluent中进行，具体表述为：采用Fluent中的用户自定义函数将线性叠加涡对作为初始条件，在1.28 m×1.28 m的正方形区域内对计算域初始化，网格规模为1 600×1 600。区域边界设置为速度入口条件，由于本次计算只是纯粹的松弛耦合过程，不考虑外部速度输入，所以速度项设置为0，而压力和温度条件则与风洞试验所记录的数据保持一致。流场求解采用无黏、非定常、基于压力的SIMPLE算法。计算总时间步数为300步，时间步长设置为0.000 1 s, 每个时间步的内迭代次数为20次，空间离散采用二阶迎风格式，时间推进采用二阶隐式格式。初始化完成后，计算域和初始流场如图6 所示,v、w是瞬态速度。

松弛计算后的流场缺少轴向速度信息，为此，采用Roy等[11, 32]对等强度同转及对转涡对的方法，获得流向速度为

图6 计算域和初始化后的流场Fig.6 Computation domain and flow field after initialization

(8)

式中：δ表示基于Lamb-Oseen涡的翼尖涡涡核半径；δG为试验测量流向速度的高斯分布特征半径；U(0,0)及ωx(0,0)为涡心处的速度和涡量。

图7为SPIV试验得到的轴向速度减少量和流向涡量与CFD计算结果，下标d和u分别代表下主涡和上主涡。可以看出，相关特征物理量符合完好。

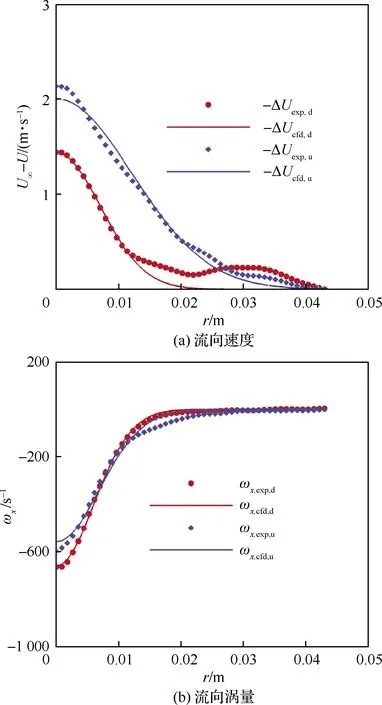
图7 SPIV试验与CFD结果比较Fig.7 Comparison of SPIV test and CFD results

基准流动是用切比雪夫谱配置点的方法将其映射到计算域内。为此，涉及到配置点数目对特征值谱的影响问题。为确定配置点数目，以α=6°、Rec=1.64×105产生的翼尖涡流场为例，分别用48×48、64×64、80×80这3套网格在扰动波数α′=1.25下进行全局稳定性分析计算，其结果如图8所示。可以发现，不同配置点数下所得到的特征值谱在稳定半平面内的树状连续分支位置基本不变，只是不稳定平面内离散点位置有所差别。对不稳定半平面中随谱配置点数变化的动点分析表明，其所对应的扰动模态为数值离散产生的计算误差，点本身为数值伪点；而不动点及其特征向量则表征具有物理意义的扰动模态。由此确定特征值谱中的两个主要模态：模态P和模态S，它们在3套网格下的特征值如表2所示。结果表明，以64×64作为计算网格能够满足分析要求。在接下来的计算中，为更明确区分开动点和不动点，所有计算和分析结果均基于56×56、64×64两套网格的结果进行。

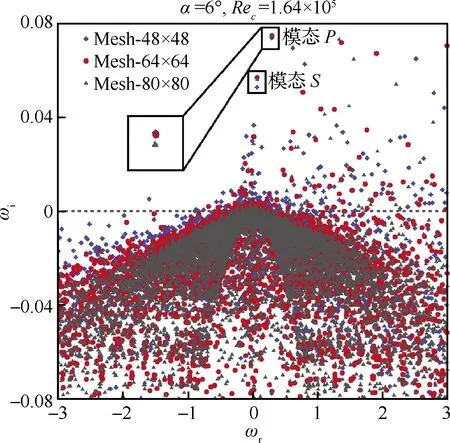
图8 配置点数无关性验证(α′=1.25)Fig.8 Validation of mesh independence (α′=1.25)

表2 不同配置点数下模态P和模态S对应的特征值对比

3 翼尖双涡结构及其不稳定性特征

3.1 翼尖双涡的结构形态

以α=8°、Rec=1.64×105为例，试验得到的时均流场如图9所示。结果表明，双叉弯刀小翼的翼尖涡为由上小翼产生的上主涡和下小翼产生的下主涡所构成的同转涡对形式。注意图中视角上方的翼尖涡为下主涡，下方的翼尖涡为上主涡。由于本试验的精心设计，该涡对近似为等强度，其中下主涡的环量为-0.299 7 m2/s，上主涡的环量为-0.321 4 m2/s；涡心坐标位置分别为(-0.003 222 m, 0.107 2 m)、(0.045 46 m, 0.049 26 m)。

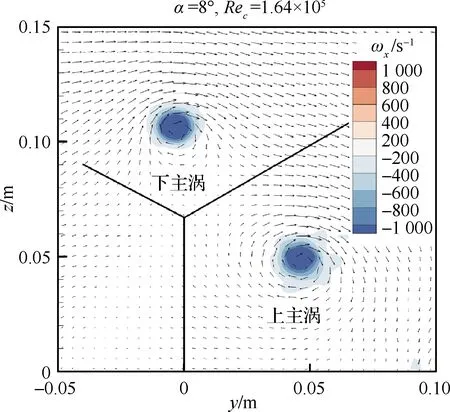
图9 试验得到的翼尖双涡时均流场云图Fig.9 Time averaged flow field contour of vortex pair from experiment

3.2 翼尖涡的不稳定特征：翼尖涡的摇摆

图10为试验中产生的同转涡对的摇摆现象，其中蓝色实线区域和黑色虚线区域分别表征翼尖涡摇摆幅值和涡核半径的圆形区域，可以看出，翼尖涡的摇摆区域始终在涡核半径范围之内。

x/c=4，10，16下，下主涡的时均涡核位置分别为(-0.018 72 m, 0.094 15 m)、(-0.006 937 m, 0.102 m)、(-0.003 222 m, 0.107 2 m)；上主涡的时均涡核位置分别为(0.081 67 m, 0.082 74 m)、(0.067 91 m, 0.057 41 m)、(0.045 46 m, 0.049 26 m)。可以发现，随着翼尖涡向远场演化，下主涡逐渐向y+、z+方向移动；上主涡逐渐向y-、z-方向移动，在这过程中，两涡逐渐靠近的同时而相互缠绕[7]。从x/c=4到x/c=16，两涡的距离从开始的0.101 m逐渐减小到0.075 68 m，而相对于y轴正方向的夹角θ则从6.48°增加到49.96°，由此可以得到该同转涡对在整个过程中的平均旋转角速度为20 rad/s。

对不同攻角、不同雷诺数下的翼尖涡摇摆幅值以对应的涡核半径无量纲化(σ/γc)，可以得到如图11所示的不同工况下的无量纲摇摆幅值随流向位置的变化规律。从图中可以看出，无量纲摇摆幅值随流向位置在逐渐增加；而上主涡的摇摆幅值总体来说均要大于下主涡的摇摆幅值，表明上主涡可能是一种更不稳定的状态。进一步地，可以发现不同工况上主涡的摇摆幅值对雷诺数和攻角变化更敏感。与NACA0015等直翼的孤立翼尖涡的摇摆幅值变化规律类似[17-18]，随着雷诺数增加，摇摆幅值也逐渐放大。然而随着攻角的变化，摇摆幅值的变化不是单调的，在α=8°下摇摆幅值最大，这可能与翼尖涡的不稳定放大率有关(详见3.3节中的讨论)。

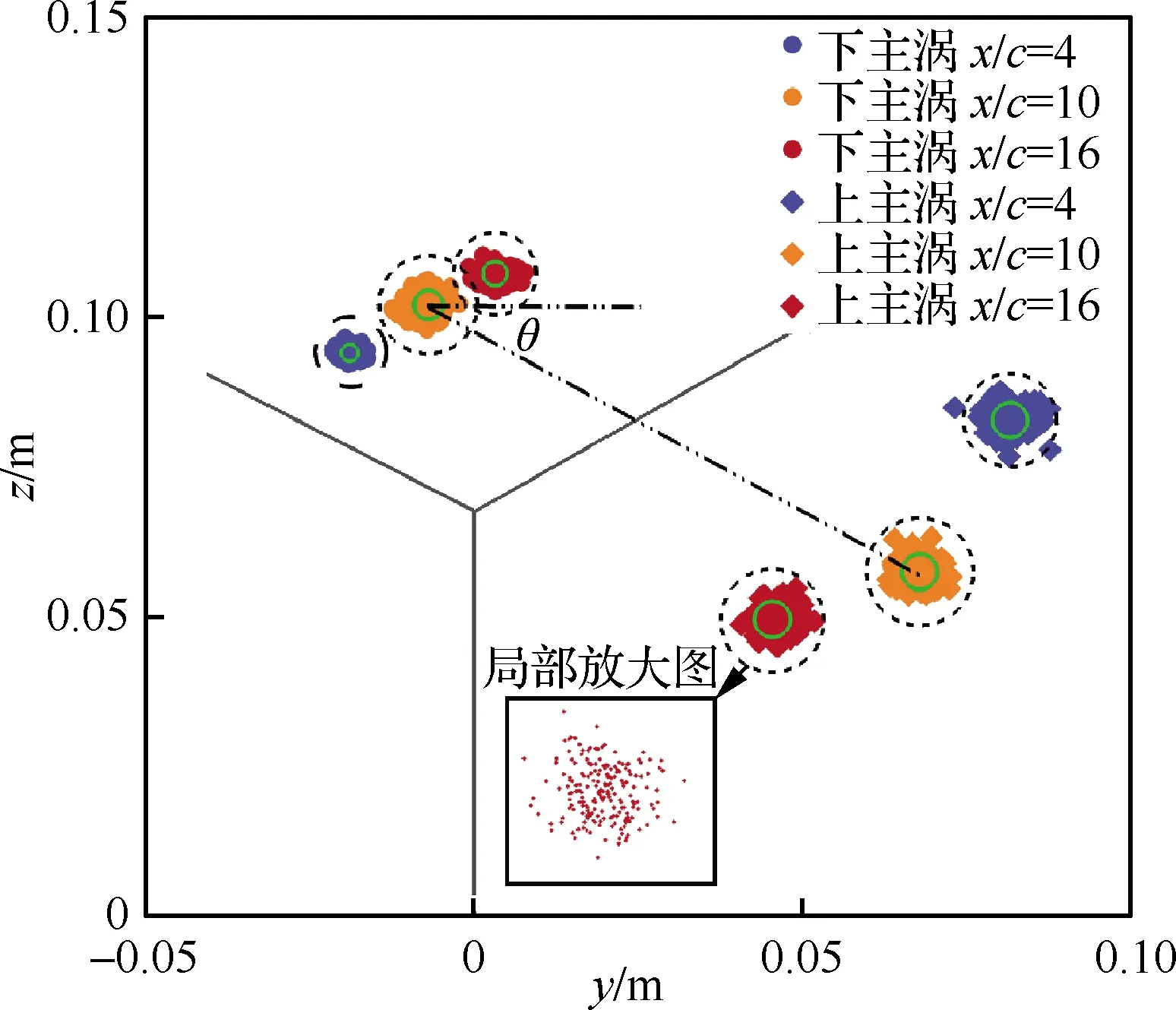
图10 翼尖双涡结构的涡核摇摆Fig.10 Vortex wandering of wingtip vortices

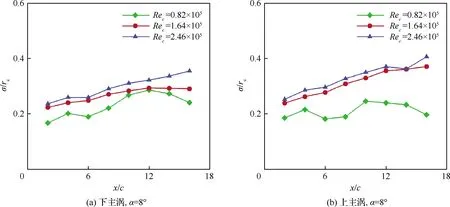
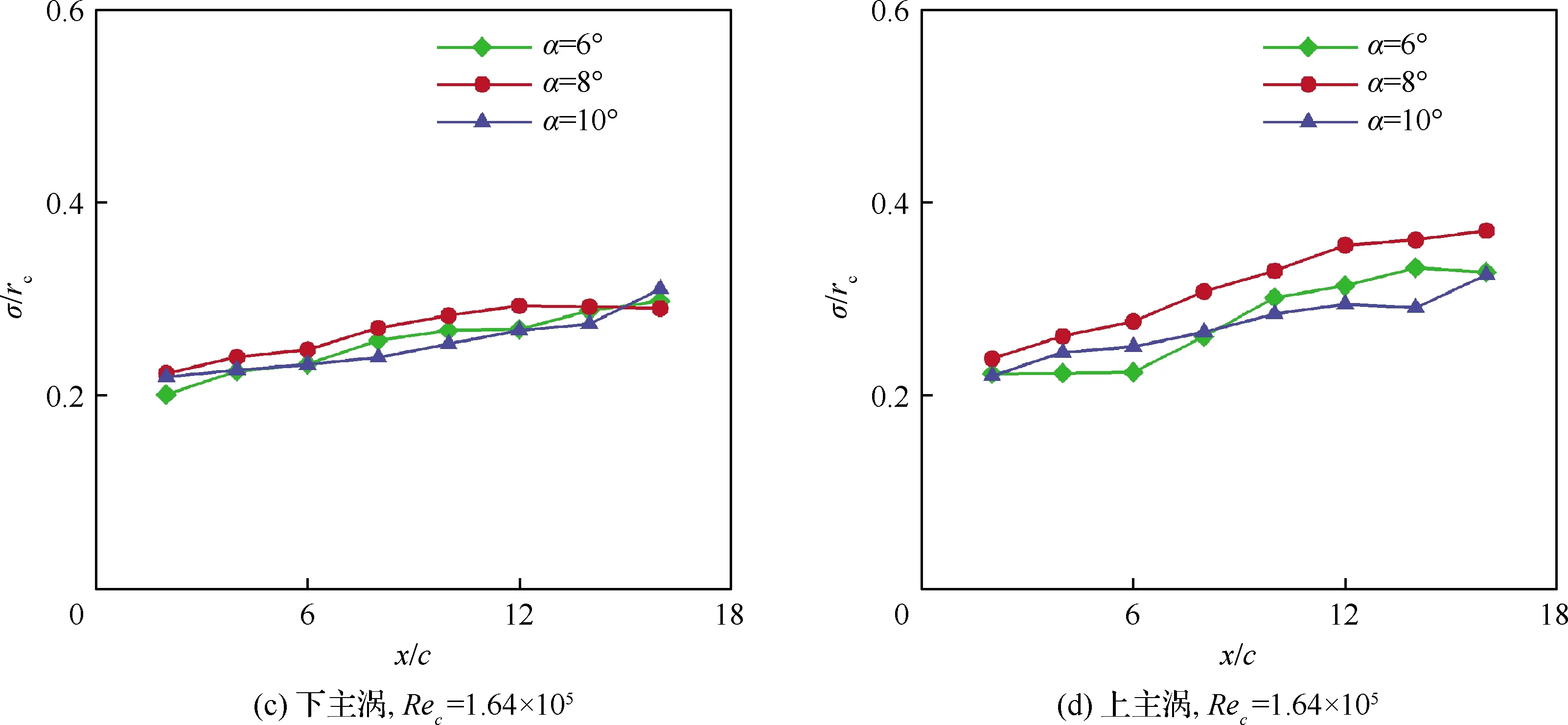
图11 不同工况下翼尖涡摇摆幅值随流向位置的变化Fig.11 Wandering amplitudes as functions of streamwise locations of wingtip vortex under different flow conditions

3.3 翼尖涡的不稳定特征：稳定性曲线

对于每一个工况而言，通过扫描不同扰动波数的特征值谱，可以得到对应的不稳定放大率，由此得到如图12所示的稳定性曲线。从图中可以发现，在各工况下，试验产生的翼尖涡的时间不稳定性放大率均大于0，这意味着翼尖涡是时间不稳定的，即扰动将随时间不断放大，超过一定阈值后扰动将使翼尖涡进入非线性发展阶段。此外，左右两列的对比结果表明，上主涡最不稳定模态(模态P)的不稳定性放大率均大于下主涡最不稳定模态(模态S)，这证明模态P在该流动中占主导地位，即上主涡的不稳定性显著强于下主涡，其扰动将随时间更快地发展而导致翼尖涡的衰减失稳。进一步分析流动条件对该双涡结构不稳定性的影响，可以发现模态P受雷诺数与攻角变化影响很大，而模态S则基本维持不变。在与图11中的结果相互印证时，也表明上主涡相对于下主涡更易于受到外界扰动的影响，是一种潜在的可调控模态。

此外，由稳定性曲线可以得到上主涡与下主涡最不稳定扰动的流向波数α′。在Rec=0.82×105～2.46×105、α=6°～10°范围内，翼尖涡最不稳定模态的扰动流向波数均分布在α′=[2.75,5]的区间内。在SPIV试验基础上经过N-S方程松弛结果得到的基于环量的特征速度Uc≈5 m/s，涡核半径δ≈0.01 m，由此可得有量纲的翼尖涡最不稳定扰动流向波数约为α*=1 800 rad/m，即沿流向每米包含约30个周期的扰动，扰动流向波长λ≈0.03 m，与翼尖涡涡核半径rc≈0.01 m可比。因此，本研究中双叉弯刀小翼产生的同转涡对所呈现的是一种短波不稳定性。

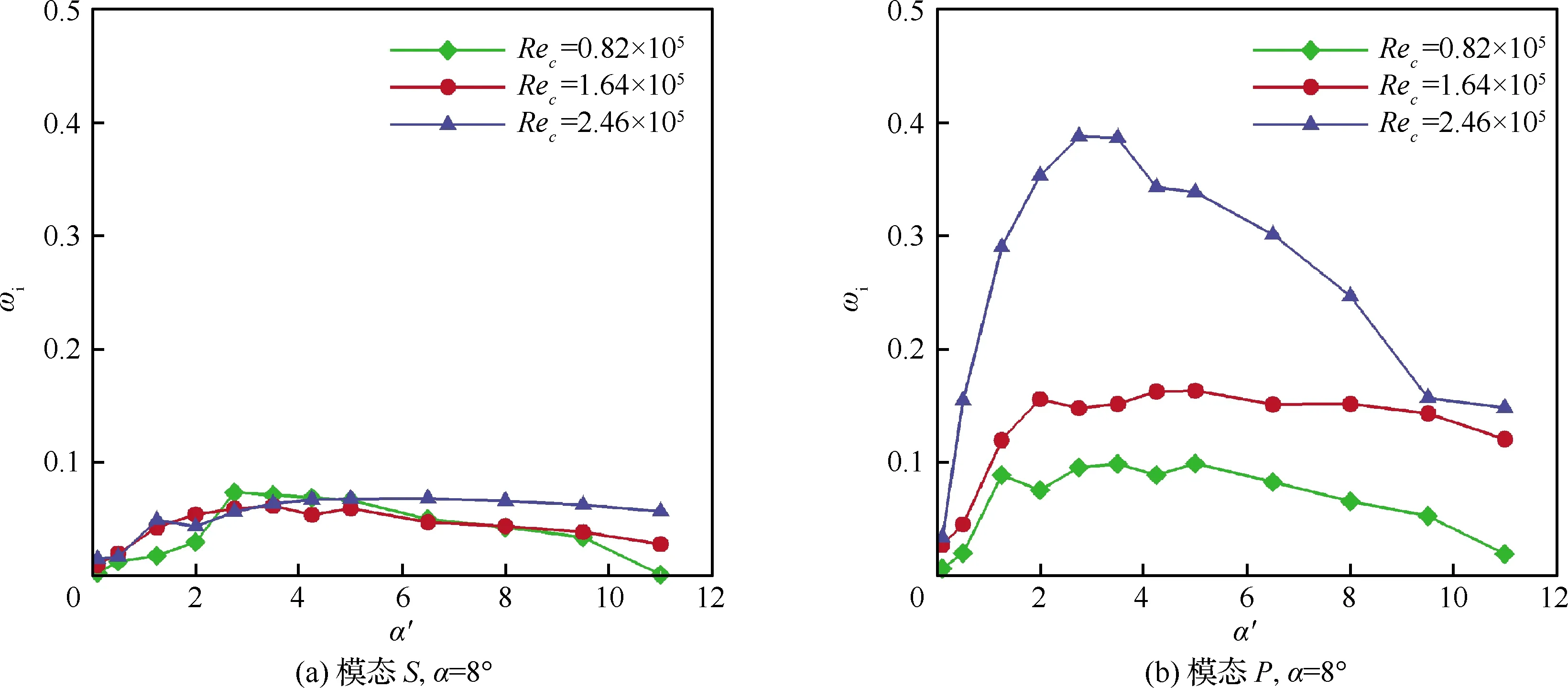
图12 各工况下翼尖涡的稳定性曲线Fig.12 Stability curves of wingtip vortex under different flow conditions

4 翼尖涡的不稳定模态演化机理

4.1 不同扰动波数下翼尖涡最不稳定模态

以α=8°、Rec=0.82×105工况为例，研究分析不同扰动波数α′下的下主涡最不稳定模态(模态P，图13)和上主涡最不稳定模态(模态S，图14)的演化行为。为显示更清晰，模态P前两个子图的无量纲显示范围分别为[-0.05,0.05]、[-0.15,0.15]，其他子图的显示范围为[-0.2,0.2]；而模态S的子图保证相同的显示范围，均保持在[-0.05,0.05]区间。

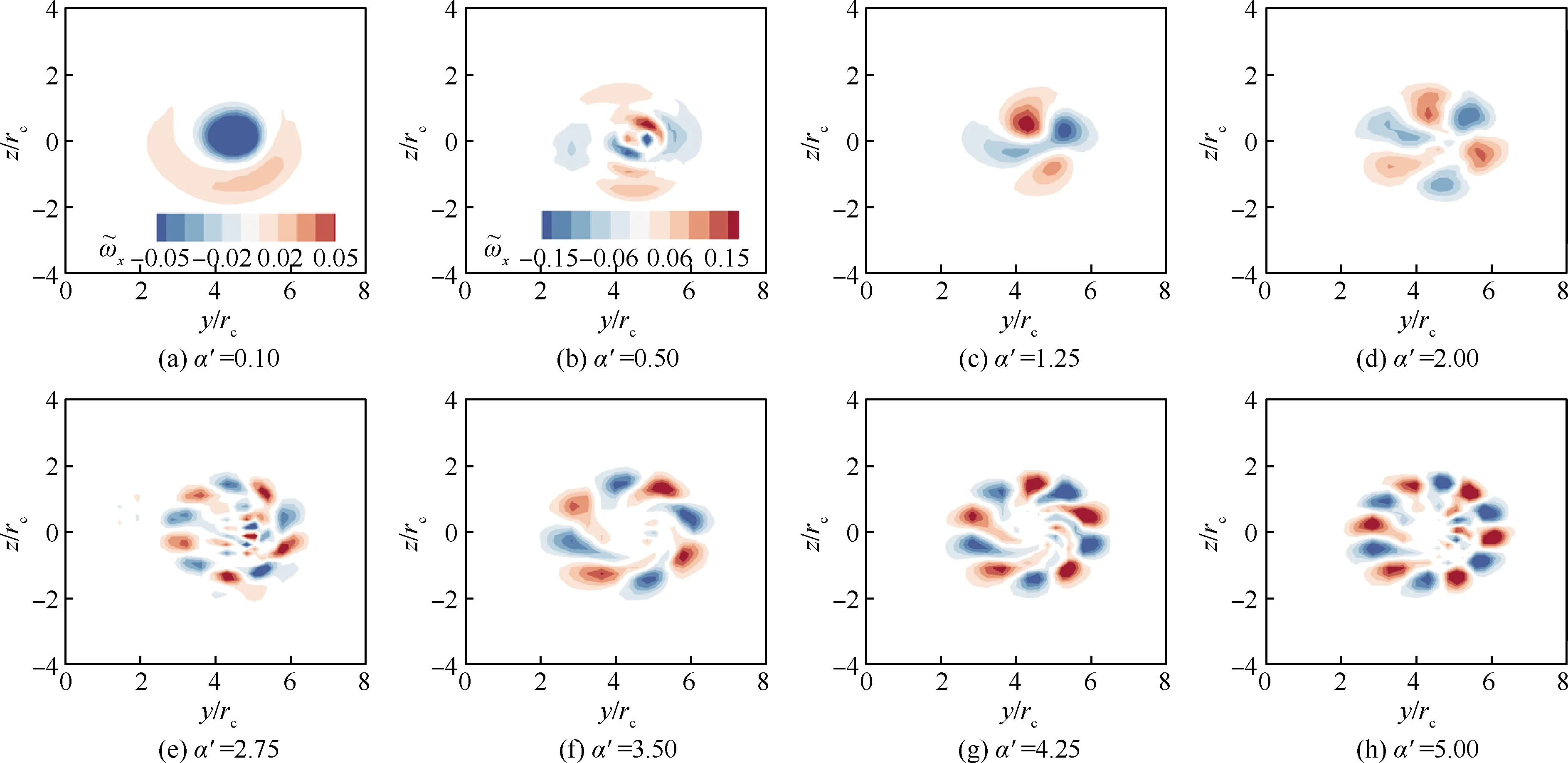
图13 不同扰动波数下模态P的演化Fig.13 Evolution of perturbation Mode P under different wavenumbers

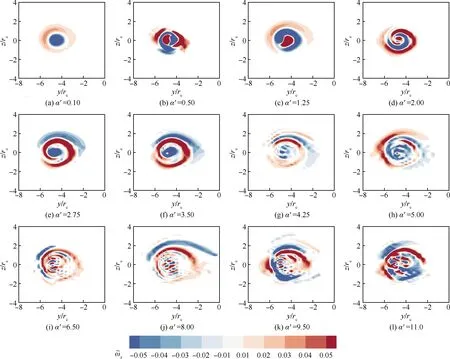
图14 不同扰动波数下模态S的演化Fig.14 Evolution of perturbation Mode S under different wavenumbers

可以发现，尽管两涡近似为等强度同转涡对，但模态P和模态S在结构特征上随着扰动波数的增加明显不同。如图13(a)和图14(a)所示，当扰动波数α′=0.1时，此时几乎没有外部扰动，模态P和模态S的形态结构一致，均为轴对称的模态，两者只有径向波数n=1，而切向波数m=0。但随着扰动波数α′的增加，模态P的切向波数也随之增大，在图13(g)中，α′=4.25时切向波数增至m=5；而α′=9.5时，m=11；但在此过程中，径向波数却变为0。对于模态S而言，扰动波数的增加改变的是径向波数n，而非切向波数。以图14 (c)中α′=1.25为例，此时径向波数n=2；当α′=5.0时，图14(d)显示的模态S径向波数至少达到n≥3。当扰动波数α′进一步增大时，模态S的径向波数已经超过64×64的切比雪夫谱配置点网格所能解析的范围，但可以预计径向波数会进一步增加。

需要指出的是，在获取上/下主涡最不稳定的模态时，要特别注意两个模态并存的耦合模态给模态识别上带来的干扰。事实上，对于耦合模态来说，类似图13和图14子图中的两种模态会分别位于各自涡核的附近区域，同时，其模态能量比下主涡的最不稳定模态的能量要强，比上主涡最不稳定模态的能量要弱。然而耦合模态在翼尖涡的演化中的作用及其调控机理尚不清楚，可在后续的工作中进一步研究。

4.2 不同工况下翼尖涡最不稳定模态

图15显示双叉弯刀式小翼翼尖涡的模态P和模态S在与基准流动相同的坐标系下的比较。图中左边为模态S，右边为模态P，可以发现模态S均准确位于下主涡涡核处，而模态P则均落在上主涡的涡核处。在各工况下，上主涡模态的扰动强度均大于下主涡，进一步表明在双叉弯刀式小翼的同转涡对中，模态P对翼尖涡不稳定性起主导作用，且其最不稳定模态均为大切向波数的扰动，各工况的切向扰动波数均达到m=5～6。对于α=10°、Rec=1.64×105条件下的最不稳定扰动模态，可以发现模态P与模态S强度较为相近，其模态之间的相对强度也与图12中稳定性曲线结果相符。

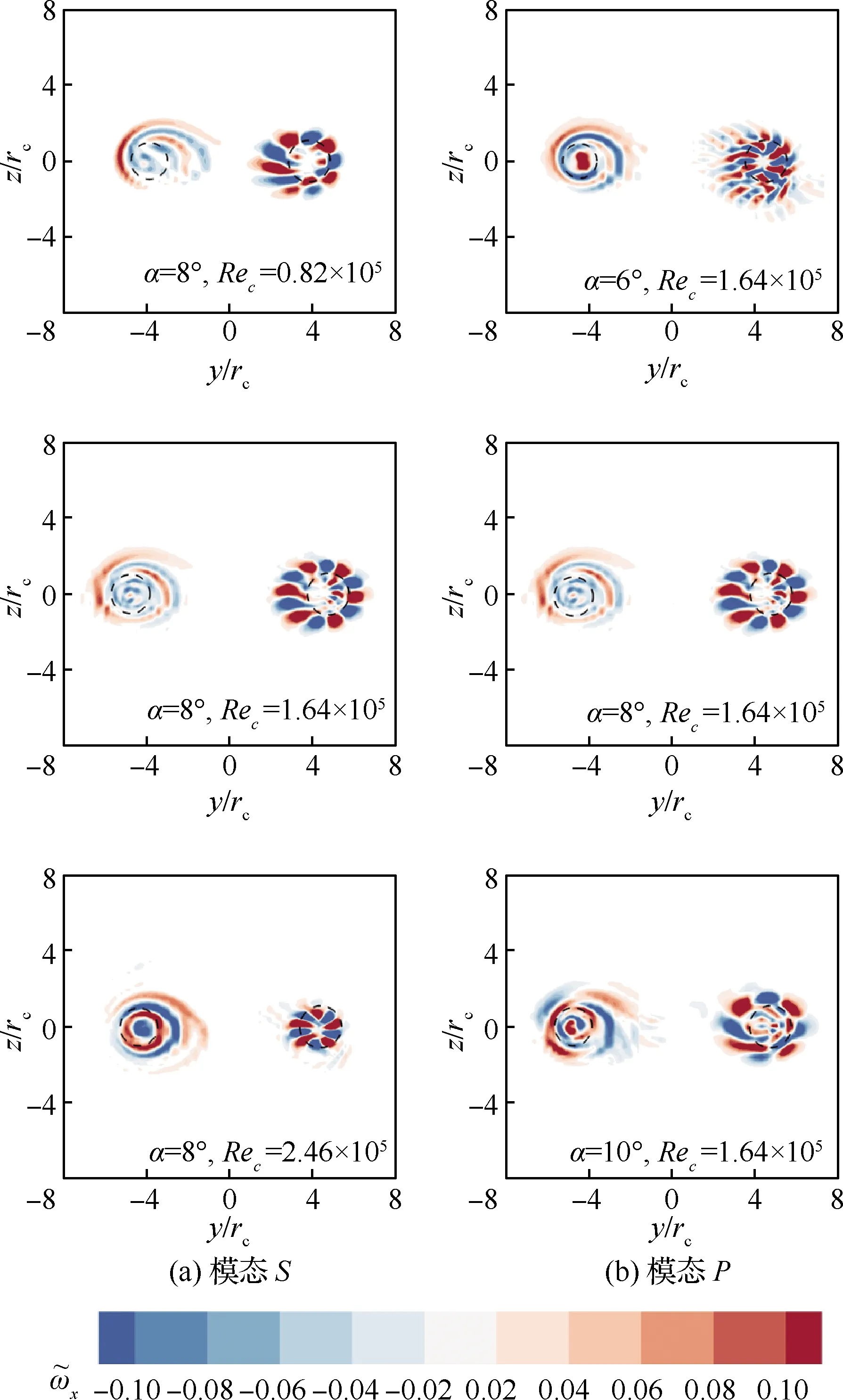
图15 不同工况下翼尖涡对的最不稳定模态Fig.15 The most perturbation modes of wingtip vortex pair under different flow conditions

图15中还标注不同工况下涡核半径的相对大小，可以发现，主涡模态的螺旋状、大切向波数扰动均紧贴涡核边界，在各工况下均有部分扰动穿透涡核边界进入涡核内部。特别地，对于α=8°、Rec=2.46×105工况，模态P扰动的绝大部分均已进入上主涡的涡核。在这种扰动模态的强作用下，该工况下的上主涡是所分析的所有工况中最不稳定的，这也与图12中稳定性曲线结果相符。

5 结 论

通过SPIV试验获得不同攻角、不同雷诺数、x/c=16范围内的双叉弯刀小翼翼尖涡流场，在CFD中经历简单的松弛阶段获得基准流动，并在此基础对其展开全局时间线性稳定性分析，得到以下结论：

1) 试验中对称布置的双叉弯刀小翼产生的翼尖涡包含上/下小翼产生的主涡(上/下主涡)结构，两者构成近似等强度的同转涡对，两者相互靠近的同时，以约20 rad/s的角速度相互缠绕。

2) 试验产生的同转涡对摇摆幅值随流向位置逐渐增大，随雷诺数的增加而增大，随攻角的增加先增大后减小。不同工况下，上/下主涡最不稳定模态(模态P/模态S)的稳定性曲线的变化规律与摇摆幅值的变化规律相一致，表明翼尖涡的摇摆源自于翼尖涡内在的不稳定性特征。

3) 在不同的扰动波数作用下，模态P与模态S的演化机理不同。增加流向扰动波数，模态P切向波数逐渐增加；而模态S则是径向波数逐渐增加。不同工况下，模态P的切向波数m=5～6，扰动流向波数分布在[2.75， 5]的区间内，对应的扰动流向波长为λ≈0.03 m，与翼尖涡0.01 m的涡核半径可比，表明试验中产生的同转涡对所呈现的是一种短波不稳定性。

4) 在不同工况条件下，模态P所对应的不稳定放大率均要大于模态S，而且对攻角、雷诺数等来流条件的改变更为敏感。不稳定放大率最大模态的扰动范围作用于上主涡的整个涡核区域，表明这种螺旋状、大切向波数的扰动模态在翼尖涡流控中的潜在价值，也表明小翼通过增加涡系的个数，可以增强不稳定的发展，实现翼尖涡快速衰减的目标。