黄雪楠， 刘锡平

（上海理工大学 理学院，上海 200093）

1 问题的提出

由于分数阶微积分在物理学、生态学、经济学等学科中具有广泛的应用，国内外学者对相关问题进行了大量的研究[1-8]。与经典的整数阶微积分不同，分数阶导数与积分需要考虑左右不同的定义，而目前对同时包含左右两个不同分数导数的微分方程的研究较少[9-11]。在现代工程技术与科学研究中，时滞对状态的影响往往是不容忽视的，因此，时滞微分方程的理论研究受到人们的重视[12-14]。

现研究一类含左右分数导数的时滞微分方程

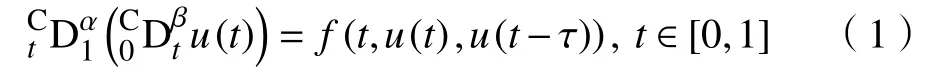
满足积分边界条件

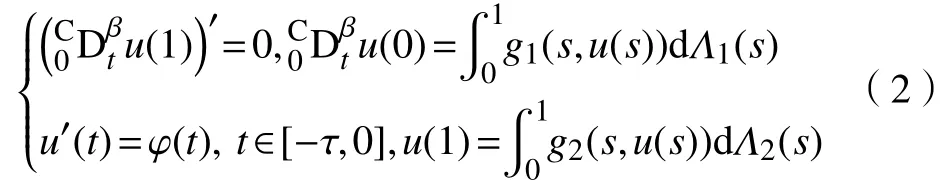
有关分数阶微积分的概念与基本性质参见文献[7-8]。本文的目的是建立一类含左右Caputo分数导数的时滞微分方程积分边值问题（1），（2）解的存在性和唯一性定理。由于Riemann-Stieltjes 积分是Riemann 积分的推广，Riemann-Stieltjes 积分边值问题以两点、多点以及一般的Riemann 积分边值问题为特例，因此，本文所研究的问题更具有一般性。本文所研究的方程在非线性项中包含了状态时滞项，该时滞项在分析系统的稳定程度和性能方面具有重要的作用，某些情况下即使时滞很小也能给系统带来严重的影响。同时含有左右分数阶导数的微分方程在许多领域都有应用，如变分原理、分数阶Lagrange 方程的极值问题、分数阶导数泛函的最优控制理论及哈密顿力学等。在文献[15-16]中，作者提出了一种用分数阶导数研究Euler-Lagrange 方程的方法，显示出分数阶微分方程在研究力学时所具有的优势。

2 预备知识

引理1设h∈C[0,1],a,b为常数，线性分数阶微分方程非齐次边值问题

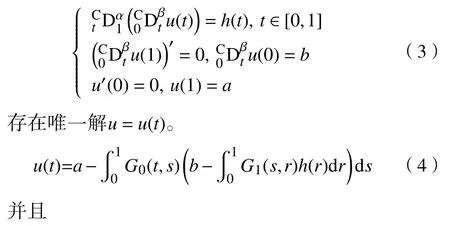
因此，边值问题（3）有解u=u(t), 并且为式（4）的形式。

反之，容易证明，若u=u(t)满足式（4），则u=u(t)满足式（3）。

由式（6）和式（7）可得引理2。

引理2对任意给定的(t,s)∈[0,1]×[0,1],G0(t,s)≥0,G1(t,s)≥ 0, 且G0(t,s),G1(t,s)在[0,1]×[0,1]上连续。

3 边值问题的上下解方法

记E=C[−τ,1], 取范数是Banach 空间。设x,y∈E, 若对任意t∈[−τ,1], 都有x(t)≤y(t), 则记x≤y。

定义1若u∈C[−τ,1]满足条件

综上所述，xk≤xk+1。

由（H1）可得

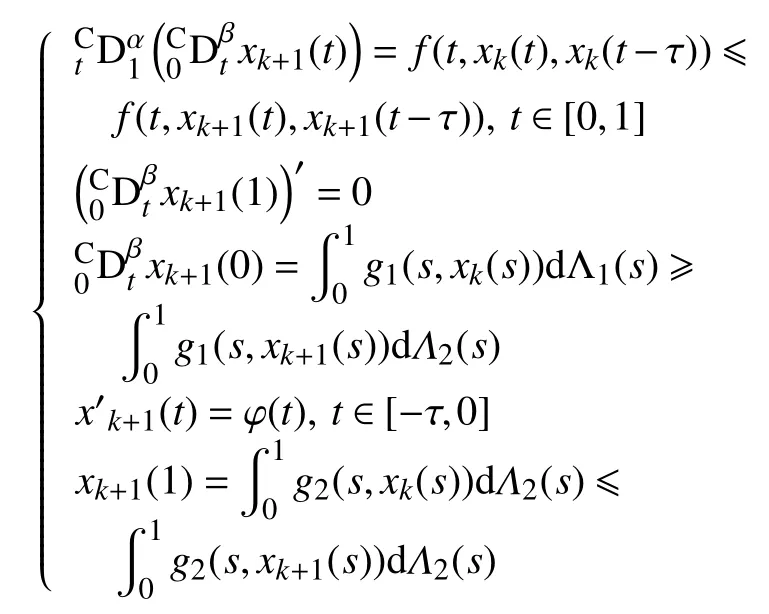
即xk+1=xk+1(t)是边值问题（10）的下解。

由引理3 可得引理4。

引理4假设（H1），（H2）成立，边值问题（1），（2）存在上解yk(t)∈E，则边值问题?

4 应用实例