杨柠玮

(四川大学数学学院，成都 610064)

1 Introduction

Three-dimensional differential systems are investigated widely because of their plentiful dynamical phenomenon. In 1963 Lorenz[1]found the first chaotic attractor in a three dimensional system. From then on，various three-dimensional systems，such as Rössler system，Chen system，Lü system，Liu system，Bao system，Pehlivan system，Jafari system and Sampath system[2-9]etc，have been proposed.

In Ref.[10]，Qietal. considered a three-dimensional nonlinear system，in which each equation contains a single quadratic cross-product term，which is described as

(1)

In this paper，we continue to study the pitchfork bifurcations in System (1) and consider thatcchanges near 1 and no mattera>1 ora≤1. Our main method is to use the parameter partition determined by the number of equilibria，which is essentially different from the center manifold method used in Ref.[11].

2 The pitchfork bifurcations

Let

Lemma 2.1(i) System (1) has five equilibriaE0,E1,E2,E3,E4if and only if (a,b,c)∈Λ1;

(ii) System (1) has three equilibriaE0,E1,E2，if and only if (a,b,c)∈Λ2∪Λ4;

(iii) System (1) has a unique equilibriumE0if and only if (a,b,c)∈Λ3∪Λ5∪Λ6，

hereE0,E1,...,E4lie at (0,0,0),(x1,y1,z1),(-x1,-y1,z1),(x2,y2,z2),(-x2,-y2,z2) respectively，and

(2)

ProofBy solving

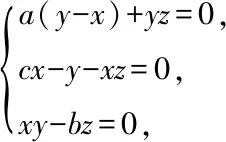
we get that

y=bcx/(x2+b),z=cx2/(x2+b)

(3)

andxsatisfies

ax5+(2ab-abc-bc2)x3+(ab2-ab2c)x=0

(4)

Obviously，x=0 is one root of (4) and all nonzero roots satisfy

ax4+(2ab-abc-bc2)x2+ab2-ab2c=0

(5)

In the following，all possible cases are considered.

(i) Ife>0,d-e>0，i.e.，(a,b,c)∈Λ1，then (5) has four distinct nonzero real rootsx1,x2,-x1,-x2，given in (2). Correspondingly，we gety1,y2,-y1,-y2,z1,z2by (3). Therefore，there are five equilibriaE0,E1,E2,E3,E4.

(ii) Ife>0,d-e≤0,d+e>0，i.e.，(a,b,c)∈Λ2，then (5) has two distinct nonzero real rootsx1,-x1given in (2). Correspondingly，we gety1,-y1,z1by (3). Therefore，there are three equilibriaE0,E1,E2.

(iii) Ife>0,d-e≤0,d+e≤0，i.e.，(a,b,c)∈Λ3，then (5) has no nonzero real roots. Thus，there is a unique equilibriumE0.

(iv) Ife=0,c>a，i.e.，(a,b,c)∈Λ4，then (5) has two distinct nonzero real rootsx1,-x1，given in (2). Correspondingly，we gety1,-y1,z1by (3). Therefore，there are three equilibriaE0,E1,E2.

(v) Ife=0,c≤a，i.e.，(a,b,c)∈Λ5，then (5) has no nonzero real roots. Thus，there is a unique equilibriumE0.

(vi) Ifeis not real，i.e.，(a,b,c)∈Λ6，then (5) has no nonzero real roots. Thus，there is a unique equilibriumE0.

Now we study the bifurcations of equilibria when parametercchanges near 1.

Theorem 2.2Let 0<ε≪1.(i) Assume thata≥1. The pitchfork bifurcation happens whencchanges from 1 to 1+ε，and the number of equilibria of System (1) changes from 1 to 3.

(ii) Assume thata<1. The pitchfork bifurcation happens whencchanges from 1 to 1-ε，and the number of equilibria of System (1) changes from 3 to 5.

ProofWhena>1 andc=1 in (2) we haved+e=0,d-e<0，i.e.，(a,b,c)∈Λ3. Whena=1 andc=1 in (2) we havee=0,a=c，i.e.，(a,b,c)∈Λ5. Thus whena≥1 andc=1，System (1) has a unique equilibriumE0by Lemma 2.1. Whena≥1 andc=1+ε，from (2) we gete>0 and

Thus (a,b,c)∈Λ2，i.e.，System (1) has three equilibriaE0,E1,E2fallows from Lemma 2.1.(i) is proved.

Whena<1 andc=1，we haved+e>0，d-e=0. Thus (a,b,c)∈Λ2，i.e.，System (1) has three equilibriaE0,E1,E2follows from Lemma 2.1. Whena<1 andc=1-ε，we gete>0 and

d-e=2a2bε/(1-a)+O(ε2)>0.

Thus (a,b,c)∈Λ1，i.e.，System (1) has five equilibriaE0,E1,E2,E3,E4follows from Lemma 2.1. From thex-coordinates ofE3,E4，we find thatE3,E4appear by the pitchfork bifurcation ofE0. (ii) is proved.

3 The stability of equilibria

In Theorem 2.2，the pitchfork bifurcation ofE0happens whencchanges near 1. In this section，we study the stability of those equilibria bifurcated fromE0.

Theorem 3.1EquilibriaE1andE2，appearing by the pitchfork bifurcation ofE0whena≥1 andcchanges from 1 to 1+ε，are locally asymptotically stable.

ProofSince System (1) is symmetric about thez-axis andE1is the corresponding symmetric equilibrium ofE2，we only need to considerE1.

Whena>1 andc=1+ε，we get

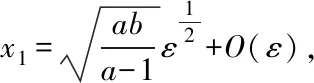
and

by (2).The Jacobian matrix atE1is given by

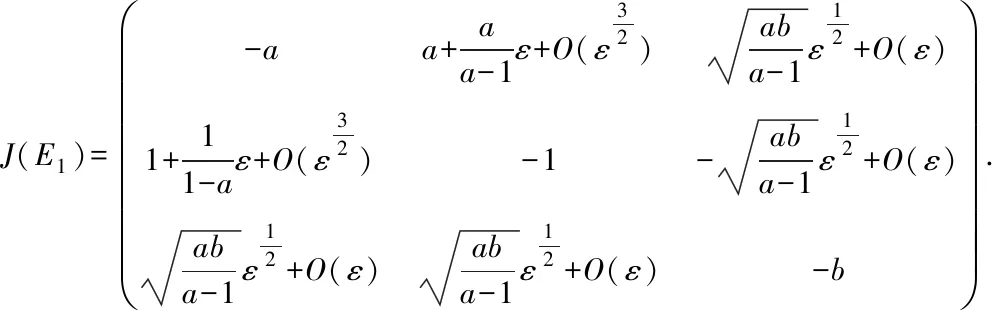
Thus the characteristic equation atE1is

whose coefficients satisfy

Then，all eigenvalues have negative real parts follows from the Routh-Hurwitz Theorem[15]. ThusE1is locally asymptotically stable，so doesE2.

Whena=1 andc=1+ε，we get

and

by (2).The Jacobian matrix atE1is

Thus the characteristic equation atE1is

λ3+(b+2)λ2+(2b+O(ε))λ+4bε+

whose coefficients satisfy

Then，all eigenvalues have negative real parts follows from the Routh-Hurwitz Theorem[15]. ThusE1is locally asymptotically stable，so doesE2.

Theorem 3.2EquilibriaE3andE4，appearing by the pitchfork bifurcation ofE0whena<1 andcchanges from 1 to 1-ε，are unstable.

ProofSince System (1) is symmetric about thez-axis andE3is the corresponding symmetric equilibrium ofE4，we only need to considerE3.

Whena<1 andc=1-ε，we get

and

by (2). The characteristic equation atE3is

(6)

whose coefficients satisfy

Then，some eigenvalues have positive or zero real parts follows from the Routh-Hurwitz theorem[15]. Obviously，there is no zero root by the expression of (6). If (6) has a pair of pure imaginary roots ±iω(ω≠0)，substitutingλ=iωinto (6) we get

i.e.,

(7)

Clearly，(7) has no solution forω. Thus (6) has eigenvalues with positive real parts. Therefore，E3is unstable，neither doesE4.