一类多项式系统的事件触发最优控制
2020-09-21楼旭阳
朱 贵,楼旭阳
(江南大学 物联网工程学院,江苏 无锡 214122)
多项式系统是一类非常重要的非线性系统,在过程控制及系统生物领域都有极其广泛的应用[1]。因此,对多项式系统的控制及其优化控制的研究一直是科学研究领域的一个热门课题。但是,由于多项式系统是一类特殊的非线性系统,求解其最优控制下的可行解显得十分困难,因此对于如何更好地获得一个求解该系统可行解的方法是多年来科学家们所研究的一个主要方向。到目前为止,基于哈密顿-雅克比不等式,以及在状态反馈控制策略下,学者们取得了一定的进展,文献[2-4]给出了对于如何有效地寻找可行解给出了各自的答案。例如,文献[2]研究了基于非线性矩阵不等式的H∞控制,文献[3]基于一类二次型Lyapunov函数和状态反馈控制策略成功获得了一类多项式系统的可行解。但是,以上所提方法的求解复杂度依旧很高,对于控制器求解不是特别直接方便。因此,本文在前人的基础上,基于哈密顿-雅克比不等式,在事件触发控制策略下,设计了一类控制器并运用平方和算法,最终得到了该系统最优控制下的一个可行解。
本文采用事件触发控制,相较于传统的时间触发控制,事件触发控制是否执行由事先给定的事件触发条件所决定,而不是根据时间周期来决定[5]。假如触发条件在某一时刻发生,则意味着控制器发出控制信号,执行器进行相应的操作。因此,可以看出,相较于传统的连续时间触发控制,事件触发控制方案可以有效地减少控制任务执行数量,在保证系统性能的基础上,有效地节约计算资源和通信资源[5]。对于多项式系统来说,之前的研究结果大多局限于一般的状态反馈和输出反馈等控制器的设计[6],基于事件触发的最优控制器的设计研究还很少。因此,本文在这方面进行了相关的研究。
此外对于多项式系统的优化控制问题,由于其非凸特性[1],对于求解其全局最优解显得十分困难。所以在求解多项式函数最优控制问题之前,首先需要先将其转化为一个凸优化问题[1]。本文采用的是基于哈密顿-雅克比不等式和状态依赖模型,将一般的多项式系统优化问题转变成求解状态依赖线性矩阵不等式问题[1],进而采用平方和算法求解状态依赖线性矩阵不等式得到其可行解。
1 问题描述
(1)
式中:x∈Rn为系统状态变量,u∈Rm为系统输入。Z(x)为一个N维的多项式状态向量,且满足只有当x=0时,Z(0)=0才成立;A(x)为多项式矩阵且满足一定的维数。B∈Rn×m是一个常数矩阵。在本文中,定义状态空间区域为Θ={x∈Rn:Z(x)TBΘZ(x)≤1},其中BΘ>0。
对于控制输入u,本文采用的是事件触发机制下的状态反馈控制器,具体形式为
(2)

(3)
式中:Z(x)表示的是当前时刻的状态信息;Z(xk-1)表示第k-1次触发时刻的状态信息,k=1,2,…。具体的事件触发条件在式(8)中给出。
此外,本文定义的误差变量形式为
(4)
由式(4)可以看出,e(x)的具体含义为:当事件触发时,该控制输入误差为0,当事件没有触发时,该控制输入误差代表上一触发时刻的控制输入减去当前时刻的控制输入所得到的控制输入误差。
引入控制输入误差变量之后,结合式(1)和误差变量式(4),式(1)可以描述成
(5)
本文设计的最优控制器主要基于如下二次型损失函数
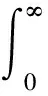
(6)
假设损失函数的最优解为J*(x0,u),可以表述成
J*(x0,u)=minJ(x0,u) ∀x0∈Θ
此外,本文还定义了该闭环系统的一个Lyapunov函数V(x)。结合Lyapunov函数V(x),本文定义了该闭环系统的一个吸引域Ω[7],形式为
Ω={x∈Rn|V(x)≤ρ}
式中:Ω⊂Θ,ρ为一个正常数。不失一般性,本文假设ρ=1。
由上述内容可知,为了求解得到最优解J*(x0,u)和最优控制器u*,需要去求解哈密-雅克比-贝尔曼方程,而直接求解这个方程是非常困难的。因此,本文通过Lyapunov函数不等式来求解损失函数的一个有限上界作为其最优解,具体的求解过程由下面的引理给出,证明过程可以参考文献[8]。
引理1[6]假设存在一个连续可微函数V:Θ→Rn和一个函数u:Θ→Rm,并满足条件V(x)>0(∀x∈Θ{0}),V(0)=0,且有
uTRu≤0 ∀x∈Θ
(7)
那么在二次型性能指标式(6)下,该系统在原点处达到了渐近稳定,并只要满足条件Ω∈Θ,则对于任意的初始值x0∈Ω,都有
J*(x0,u)≤J(x0,u)≤V(x0)
可知,找一个合适的Lyapunov函数V(x)会使求解该控制器的问题成为一个凸优化的问题,但是寻找这样一个合适的Lyapunov函数V(x)和控制器u还是一件十分困难的事。本文将利用平方和算法给出其设计过程。
注1假设f(0)=0且f(x)可以表示成f(x)=A(x)x,进一步可以表示成
2 主要结果
2.1 平方和算法
定义1[9]对于一个多变量多项式p(x1,…,xn)=p(x),如果存在多项式f1(x),…,fm(x),使得
则称p(x)是平方和多项式(SOSP)。
引理2[10]多项式p(x)是SOSP,当且仅当存在一个半正定矩阵H,使得
p(x)=Z(x)THZ(x)
式中:Z(x)是关于x的单项式向量。
由定义1和引理2可知,若多项式p(x)是SOSP,则p(x)≥0,所以SOS条件是判断一个多项式是否是非负定的一个充分条件。虽然只是一个充分条件,然而数值仿真实验表明,该方法带来的保守性很小,也已有学者证明,在某些情况下,多项式非负与该多项式SOS二者是等价的[10]。
2.2 事件触发控制
在设计事件触发控制器之前,需要先定义一个事件触发条件。本文设计的事件触发条件为
‖e(x)‖≤σ‖K(x)Z(x)‖
(8)
式中:σ为一个正常数,且取值范围为0<σ<1。
结合式(8),式(3)可以描述成为
(9)
为了满足上述引理1中的限制条件,本文选取的Lyapunov函数V(x)为
V(x)=Z(x)TP-1Z(x)
(10)
式中:P为一个对称正定矩阵,即P>0。在此基础上,吸引域Ω可以进一步表示成如下形式
Ω={x∈Rn|Z(x)TP-1Z(x)≤1}
此外,定义M(x)是一个N×n的矩阵,其中矩阵每个元素的定义为
结合上述讨论和已知条件,给出本文的主要结果。
定理1给定Q>0,R>0,若存在一个对称正定矩阵P>0满足如下条件
(11)
(12)
(13)
式中
Φ(x)=-(M(x)A(x)P+PA(x)TM(x)T)-
式(12)中I是满足一定维数的单位矩阵,则式(1)在式(2)的作用下,使得闭环系统原点渐近稳定,其中,K(x)=-R-1BTM(x)TP-1,λmax(R)和λmin(R)分别表示矩阵R的最大特征值和最小特征值。同时,对于任意的初始值x0∈Ω,满足
J*(x0,u)≤J(x0,u)≤V(x0)
证明由条件式(11)可知,吸引域Ω满足条件Ω⊂Θ。由式(2)和(4)可得u=K(x)Z(x)+e(x)。将Lyapunov函数式(10)以及K(x)=-R-1BTM(x)TP-1代入式(7)可得
2Z(x)TP-1M(x)(A(x)Z(x)+BK(x)Z(x)+
Be(x))+Z(x)TQZ(x)+(e(x)+K(x)Z(x))T·
R(e(x)+K(x)Z(x))=Z(x)T(2P-1M(x)A(x))·
Z(x)+Z(x)T(2P-1M(x)BK(x))Z(x)+
Z(x)T(2P-1M(x)B)e(x)+Z(x)TQZ(x)+
e(x)T(RK(x))Z(x)+Z(x)T(K(x)TR)e(x)+
Z(x)T(K(x)TRK(x))Z(x)+e(x)TRe(x)=
Z(x)T(2P-1M(x)A(x)+Q)Z(x)-
Z(x)T(P-1M(x)BR-1BTM(x)TP-1)Z(x)+
e(x)TRe(x)
(14)
由式(8)以及K(x)=-R-1BTM(x)TP-1,可得
e(x)Te(x)≤σ2Z(x)TΨZ(x)
(15)
式中:Ψ=P-1M(x)BR-1R-1BTM(x)TP-1。
将式(15)代入式(14),可得
Z(x)T[2P-1M(x)A(x)+Q-P-1M(x)BR-1BTM(x)TP-1]·
Z(x)+e(x)TRe(x)≤Z(x)T[2P-1M(x)A(x)+
Q-P-1M(x)BR-1BTM(x)TP-1]Z(x)+
P-1M(x)BR-1BTM(x)TP-1]Z(x)
(16)
利用Schur补引理以及Φ(x)的定义,式(12)等价于
M(x)A(x)P+PA(x)TM(x)T+PQP+
对上式分别进行左乘和右乘矩阵P-1,可得
P-1M(x)BR-1BTM(x)TP-1≤0
(17)
将式(17)代入式(16),可得
uTRu≤0
所以式(7)成立。又由于Z(0)=0,所以V(0)=0。由V函数定义可知,V(x)>0(∀x∈{Θ0})。从而,由引理1知,闭环系统在原点渐近稳定。利用Schur补引理,条件式(13)等价于Z(x0)TP-1Z(x0)≤1,即x0∈Ω,则可得J*(x0,u)≤J(x0,u)≤V(x0)成立。证毕。
注2本文考虑的是多项式系统在事件触发下的最优控制问题,而没有考虑一般状态反馈控制下的稳定性问题。一个最主要的原因是在那种情况下,会得到一个双线性矩阵不等式(BMI)的充分条件,求解十分困难[11,12]。考虑在二次型损失函数下最优控制时,本文能够得到一个状态依赖线性矩阵不等式(LMI)条件,且能用MTALAB工具箱SOSTOOLS[13]求解得到可行解。
注3相比于连续时间控制,事件触发控制可以节约大量的控制资源,同时也较为容易的在硬件设备上实现,有利于工程实践中的硬件设计和系统控制的实现。
3 仿真算例
本节给出两个具体的仿真算例来说明所提方法的有效性。
例1下面以Lorenz系统[14]为对象进行研究,它是一个典型的混沌系统,具体形式为
(18)
式中:x为状态变量,a、b和c为系统参数,u1和u2为控制信号。该系统可以转化成式(1)的形式,其中
B=[1,1,0]T
当无控制作用时,即u1=u2=0,且a=10,b=28,c=8/3时,式(15)的状态相位图如图1所示。
由图1可以看出,Lorenz系统呈现出混沌状态。利用定理1,本文设计事件触发控制器式(2),其中参数如下,a=10,b=28,c=8/3,Q=I,R=1,BΘ=1.78I,σ=0.5,其中I是3×3的单位矩阵,取初始值x0=[0.456,0.523,0.675]T,则利用平方和算法可得控制器为
u1=u2=-122.5762x1-110.9763x2+0.0004x3
且
在此控制器作用下,可以得到如图2所示的结果。由图中可以看出,在事件触发控制下,该系统能很快地趋于稳定,说明了所设计控制器的有效性。事件触发间隔如图3所示。
为了说明该控制方法的优点,本文还给出了该系统在时间触发控制情况下的系统状态,在时间触发控制下,其控制信号间隔时间由控制总时间和该段时间内的触发总次数决定,而时间触发控制下的触发总次数与事件触发控制下相同控制时间的触发总次数相同,轨迹如图4所示。比较图2和图4可以看出,事件触发控制下系统状态的收敛速度要快于时间触发控制下的收敛速度,进一步说明了事件触发控制器的优势。
例2下面这个例子是以Chua’s混沌系统[15]为研究对象,其系统状态方程为
(19)
式中:x为状态变量,α和β为系统参数,u为控制信号,f(z)为一个分段线性函数,具体形式为
f(z)=dz+0.5(d-e)(|z+1|-|z-1|)
式中:d和e为两个常数,并且满足d 同样地,Chua’s系统也可以转换成式(1)的形式,其中 B=[1,0,0]T 不考虑控制作用,即u=0时,取参数α=9.215 6,β=15.994 6,d=-1.249 05和e=-0.757 35,该系统呈现出混沌状态,效果如图5所示。 仿真中,取Q=2.5I,R=1,BΘ=0.9070I,σ=0.09,且I是一个3×3的单位矩阵,初始值x0=[0.15,0.1,0.2]T。由于f(z)是一个分段线性函数。所以,分三部分进行控制器的设计,当x1<-1时,可得控制器u=-24.1084x1-19.0293x2-9.2791x3+47.5972以及 当|x1|≤1时,可得控制器u=-65.6889x1-60.1526x2-9.8241x3且矩阵 当x1>1时,可得控制器u=-24.1084x1-19.0293x2-9.2791x3-47.5972和 在上述控制器作用下,控制效果如图6所示。从图6可以看出,约3.5 s后,系统状态收敛到原点。事件触发间隔如图7所示。 同样地,在时间触发控制下,得到图8的结果。从图中可以看出,系统状态收敛到原点需要5 s,收敛速度明显慢于事件触发控制下系统的收敛速度,从而说明了事件触发控制的优势。 本文以一类输入仿射多项式系统为研究对象,基于状态依赖模型和哈密顿-雅克比不等式成功构造了状态依赖线性矩阵不等式,与一般状态反馈控制不同,本文还采用了能有效减少计算资源的事件触发控制来研究多项式系统的最优控制。最后,基于一类事件触发控制策略和平方和算法求解得到了一个可行解,并验证了其有效性。4 结论
