沈莞蔷，王宏凯

Bézier曲线的多项式重新参数化检测

沈莞蔷，王宏凯

(江南大学理学院，江苏 无锡 214122)

研究了一种用于精确检测一条Bézier曲线的次数是否可以通过多项式重新参数化降低的算法。该算法对任意一条Bézier曲线，将重新参数化前后的基函数的关系用方程组的形式表达，但不需要解方程，而是通过系数表示的金字塔算法直接计算，可以精确求出用于重新参数化的多项式和降低次数后的Bézier曲线的控制顶点，并且该重新参数化的多项式在相差一个线性变换的前提下是唯一的。通过实例应用，该算法运算速度较之前的算法快。

Bézier曲线；多项式；重新参数化；基函数；金字塔算法

Bézier曲线凭借优良的造型性质，在几何设计中有着重要应用[1-2]。由于在参数曲线中，参数选择的多样性，有些参数化会使得一些Bézier曲线出现不适当的情况[3]，一旦使用了合适的参数化，Bézier曲线可以精确转换为低次的Bézier曲线，相比高次Bézier曲线，低次Bézier曲线具有数据量少[4]、计算更快[5]、更好的系统兼容性[6-7]、对多边形曲线的控制性更强[8-9]等优点。

已有文献在不改变曲线参数化的情况下，对Bézier曲线降次，如文献[10]通过选取合适的函数，在不受拐角插值约束的条件下，实现了形状参数可调的SG-Bézier曲线的降次；文献[11]提出一种基于约束对偶Bernstein多项式，是计算降次Bézier曲线控制顶点的方法；文献[12]用L2范数连续分段多项式曲线求解有理Bézier曲线逼近问题；文献[13]利用Bézier曲线本身的升次性质，结合广义逆矩阵的最小二乘理论，给出了一种新的降次逼近方法；文献[14]利用3次PH曲线来逼近代数曲线；文献[15]基于端点约束的Bézier曲线降次方法，为了保证曲线的平滑程度，在常规目标函数的基础上，提出了附加平滑项的Bézier曲线生成方法；文献[16]阐述了以高阶导消失为B样条曲线自身退化的条件，利用约束优化逼近原曲线。

事实上，一条多项式曲线有许多种参数形式，有些高次的曲线通过重新参数化可精确的以低次的形式表示，文献[3]将原高次曲线的参数化称为不适当的。这种改变参数化降阶的相关工作主要有：文献[17]和文献[3]使用类似求最大公约式的辗转相除法，检测多项式曲线参数化是否适当；文献[18]使用分段线性参数，对Bézier曲线进行降次，取得了更好的逼近效果；文献[19]给出了2条Bézier曲线完全重合的条件。

针对Bézier曲线参数化是不适当[3]的情况，本文给出了一种算法，即检测Bézier曲线的参数化是否是不适当的，如果是，将给出重新参数化后的Bézier曲线的控制顶点和相应的重新参数化多项式；同时与文献[3]的算法相比，并经实例应用对比表明，本文算法有更快的运算速度。

1 理论分析

如果()是DRPR曲线，那么()的LD的Bézier曲线可记为

与文献[3]相同，本文将Bernstein基转化为幂基的形式。基转换有2个目的：①为了排除在Bernstein基下最高次项系数为0的自身退化的情况；②在幂基形式，利用高次基(包括低次基作为子集)以及同次基中函数的次数差异性，在后续构造金字塔时，避免进行反求方程。

检验式(4)是否为DRPR，有

其中，=[01···]。由式(4)和式(6)，以及的线性无关性，得到

1.1 重新参数化多项式

重新参数化多项式()具有如下性质。

性质 1.如果()是曲线式(4)的重新参数化多项式，则()的任意线性变换，如()+(,Î,且≠0)，也是式(4)的重新参数化多项式。

证明：由题意知

其中

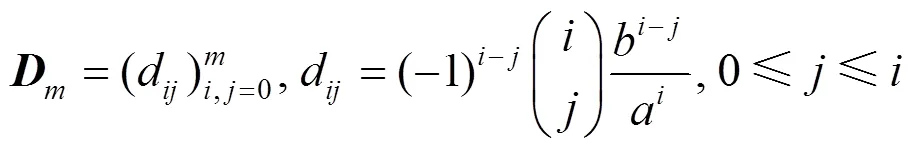
证毕

证明将在1.3节给出。

1.2 基表示矩阵

其中，①是考虑多项式S()的次数得到的，=0,1,···,；②是显然的；③是S≠0的结果；④可以由①通过数学归纳法证明得到。

性质 4. 在曲线式(4)为DRPR的情况下，如果次重新参数化多项式()确定，那么矩阵是唯一的。

1.3 方程的解

根据性质3的①，式(7)中的方程组为

在式(9)中，初始的行，每行有个方程，最后一行有1个方程，由该方程组可以依次解出,–1,···,1,0。

根据性质1，不失一般性，令()中0=0，S=1。有a=0 (0≤<≤)，且a,ik=1 (0≤≤)，根据性质3的②，若式(4)为DRPR，则有

满足式(9)的第一行的第一个方程和最后一行的方程。

命题1. 如果式(4)为DRPR，那么向量–1,···,–k+1均为的倍数，其中为重新参数化多项式的次数。

该命题给出了一种求的方法，由于在初始的Bernstein基形式(1)中，单点和直线段的情况均很容易判断，所以=的情况可以单独考虑。另外，=1的情况不会降低式(4)的次数。所以，只考虑的非平凡约数。当式(4)中的给定时，有如下性质。

性质5.如果式(4)是DRPR，那么任意可用于重新参数化的多项式的次数，均要满足：

①是的一个非平凡约数；

②≤，其中是满足–1,–2,···,–l+1都是的倍数这个条件的最大值。

此外，希望找到式(4)的MD曲线，即取最大值，在下一节的算法中，的取值从大到小列出。同时，如果不存在满足条件的，则式(4)为非DRPR。

为了解出S,=1,2,···,–1，仍然考虑式(9)的第一行方程，对于的每一个候选值，–1,–2,···,–l+1均为的倍数，并且≠0，记向量中首个不为0的分量为，对应的分量为，其中,,，根据式(9)的第一行方程可得

性质3的②与④表明，通过金字塔算法可计算a，其算法路径为

即

同样的，当=–2,–3,···,1，存在

其中，c,n–k+j为(S+1t+1+S+2t+2+···+St)展开式中t–k+j前的系数。因此，c,n–k+j的值可以通过a用同样的金字塔算法得出，所以有

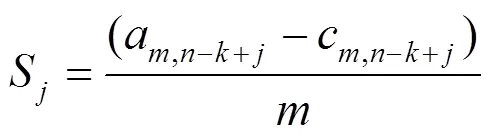
其中

并且00=1，根据上述计算可看出：S,=–2,–3,···,1可通过S+1, S+2,···,S得到。所以性质2的证明如下：

证明：若式(4)为DRPR，由于性质1，如果0和S都是固定的，那么，S,=–2,–3,···,1均是唯一的，因此，性质2成立。

证毕

计算其余，当=–1,–2,···,1，根据式(9)的第一列方程，依次有

另外，得到后，式(9)的第+1–行中就没有未知数了。然后检查方程是否成立，排除非DRPR的情况。

目前曲线式(4)有2种情况：

(1) 非DRPR；

(2) DRPR，可求得式(4)的MD曲线的控制顶点矩阵，以及重新参数化多项式()。

最后，用一个简单方法控制重新参数化多项式()的值域，使得该值域为[0,1]，记，分别为()在[0,1]的最大值和最小值，则

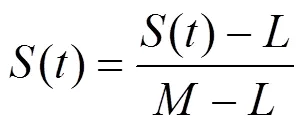
并且

其中，为式(8)中的矩阵，且=1/(–)，=–/(–)。

2 算 法

本文算法需首先考虑单点和直线段的特殊情况。

2.1 特殊情况

在Bernstein基形式(1)下直接考虑特殊情况。

并且

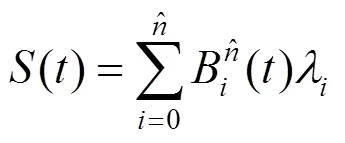
2.2 算法实现

算法：检测Bézier曲线是否为DRPR。

(1) 若为单点，可根据输入的控制顶点个数进行判断。

(2) 若是共线，可根据输入的控制顶点个数进行判断。

步骤4. 对于的每一个候选值：

(2) 根据式(11)，依次得到a,j,=–1,–2,···,–+1的值。

(3) 根据式(12)，得到S–1的值，根据式(13)，依次计算得到S–2, S–3,···,1的值。

(4) 根据性质3中的②和④，计算出其余的a,=1,2,···,–1,=,+1,···,，当=时，=,+1,···, (–1)。

(5) 当=–1,=–2, ···,1时，

①根据式(15)，计算。

(6) DRPR=T，根据式(3)得到()，跳出当前循环。

3 实 例

实验环境见表1，每个实例中，用红色空心圈表示输入的Bézier曲线()的控制顶点，用蓝色虚线表示对应的控制多边形，用蓝色粗实线表示曲线()，用绿色方块表示Bézier曲线()的控制顶点，用粉色虚线表示对应的控制多边形，用粉色细实线表示曲线()。

表1 实验环境

例1．输入Bézier曲线的控制顶点

经算法得DRPR=，重新参数化多项式

其中，MD的Bézier曲线的控制顶点为：，如图1所示。

图2 平面4次非DRPR曲线

例3. 输入Bézier曲线的控制顶点：

经算法得DRPR=。重新参数化多项式

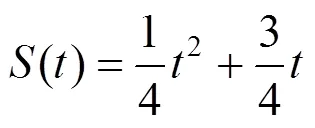
其中，MD的Bézier曲线的控制顶点为：，如图3所示。

例4. 输入Bézier曲线的控制顶点：

经算法得DRPR=T，重新参数化多项式为

曲线()在Bernstein基下控制顶点为：

图4 平面6次DRPR曲线

Fig. 4 DRPR planar curve of degree 6

最后将本文算法与文献[3]的算法进行比较。文献[3]的算法，输入和输出是幂基下的多项式曲线的顶点，所以本文对比的时间是从曲线转换为幂基形式之后(即步骤2)开始计时，到程序输出重新参数化多项式()和幂基形式下顶点(即步骤5)结束计时。时间对比见表2。

表2 算法运行时间对比(s)

4 结束语

本文给出的算法可以用来判断任意一条Bézier曲线是否为DRPR，若是DRPR，可以精确求出该曲线的MD的Bézier曲线的控制顶点，以及相应的重新参数化多项式。

本文的算法用于精确判断曲线是否为DRPR的情况，但是，大部分的Bézier曲线均是非DRPR的。在后续的工作中，将研究给定Bézier曲线的近似DRPR逼近算法，即通过控制顶点微小扰动，使得非DRPR曲线变为DRPR曲线。

[1] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M]. 北京: 高等教育出版社, 2001: 249-250. WANG G J, WANG G Z, ZHENG J M. Computer aided geometric design[M]. Beijing: Higher Education Press, 2001: 249-250 (in Chinese).

[2] 郭大勇, 成佳颐. 基于二项式系数设计矩阵的Bézier 曲线扩展[J]. 图学学报, 2014, 35(4): 511-517.GUO D Y, CHENG J Y. Extension of Bézier curve based on the design of matrix using binomial coefficient[J]. Journal of Graphics, 2014, 35(4): 511-517 (in Chinese).

[3] SEDERBERG T W. Degenerate parametric curves[J]. Computer Aided Geometric Design, 1984, 1(4): 301-307.

[4] 胡倩倩, 王国瑾. 球域Bézier曲面的精确边界及其多项式逼近[J]. 浙江大学学报: 工学版, 2008, 42(11): 1906-1909. HU Q Q, WANG G J. Exact boundary of ball Bézier surface and its approximation by polynomial form[J]. Journal of Zhejiang University: Engineering, 2008, 42(11): 1906-1909 (in Chinese).

[5] QIAO Z F, HU M, TAN Z H, et al. An accurate and fast method for computing offsets of high degree rational Bézier/NURBS curves with user-definable tolerance[J]. Journal of Computer Languages, 2019, 52: 1-9.

[6] RABABAH A, IBRAHIM S. Gometric degree reduction of Bézier curves[C]//International Conference on Mathematics and Computing. Heidelberg: Springer, 2018: 87-95.

[7] 胡倩倩. 曲线曲面的两类几何逼近与两类代数表示[D]. 杭州: 浙江大学, 2008. HU Q Q, Two kinds of geometric approximations and algebraic representations of curves and surfaces[D]. Hangzhou: Zhejiang University, 2008 (in Chinese).

[8] CHEN Y, CAI Y Y, ZHENG J M, et al. Accurate and efficient approximation of clothoids using Bézier curves for path planning[J]. IEEE Transactions on Robotics, 2017, 33(5): 1242-1247.

[9] HAN X L, GUO X. Optimal parameter values for approximating conic sections by the quartic Bézier curves[J]. Journal of Computational and Applied Mathematics, 2017, 322: 86-95.

[10] HU G, QIAO Y, QIN X Q, et al. Approximate multi-degree reduction of SG-Bézier curves using the grey wolf optimizer algorithm[J]. Symmetry, 2019, 11(10): 1242-1260.

[11] GOSPODARCZYK P, LEWANOWICZ S, WOŹNY P. Degree reduction of composite Bézier curves[J]. Applied Mathematics and Computation, 2017, 293: 40-48.

[12] ESLAHCHI M R, KAVOOSI M. The use of Jacobiwavelets for constrained approximation of rational Bézier curves[J]. Computational and Applied Mathematics, 2018, 37(3): 3951-3966.

[13] 陈国栋, 王国瑾. 基于广义逆矩阵的Bézier曲线降阶逼近[J]. 软件学报, 2001, 12(3): 435-439. CHEN G D, WANG G J. Degree reduction approximation of Bézier curves by generalized inverse matrices[J]. Journal of Software, 2001, 12(3): 435-439 (in Chinese).

[14] 寿华好, 江瑜, 缪永伟. 基于三次PH曲线误差可控代数曲线等距线逼近算法[J]. 图学学报, 2012, 33(2): 30-33. SHOU H H, JIANG Y, MIAO Y W. Error controllable algebraic curve offset approximation based on cubic PH curve[J]. Journal of Graphics, 2012, 33(2): 30-33 (in Chinese).

[15] HAN X L, YANG J. Multi-degree reduction of Bézier curves with distance and energy optimization[J]. Journal of Applied Mathematics and Physics, 2016, 4(1): 8-15.

[16] YONG J H, HU S M, SUN J G, et al. Degree reduction of B-spline curves[J]. Computer Aided Geometric Design, 2001, 18(2): 117-127.

[17] SEDERBERG T W. Improperly parametrized rational curves[J]. Computer Aided Geometric Design, 1986, 3(1): 67-75.

[18] CHEN X D, MA W Y, PAUL J C. Multi-degree reduction of Bézier curves using reparameterization[J]. Computer-Aided Design, 2011, 43(2): 161-169.

[19] CHEN X D, YANG C, MA W Y. Coincidence condition of two Bézier curves of an arbitrary degree[J]. Computers & Graphics, 2016, 54: 121-126.

Polynomial reparameterization detection of Bézier curves

SHEN Wan-qiang, WANG Hong-kai

(School of Science, Jiangnan University, Wuxi Jiangsu 214122, China)

An algorithm is presented to determine whether the degree of Bézier curve can be reduced by polynomial reparameterization. In the algorithm, for any Bézier curve, the relation between the basis functions before and after reparameterization is expressed as a system of equations. Instead of solving the equations,the polynomial for reparameterization and the control points of the lower degree Bézier curve can be calculated directly by apyramid algorithm of coefficient reparameterization.In addition,the polynomial for reparameterization is unique to within a scale factor and a constant. Compared with the previous algorithm by examples, this algorithm possesses shorter computational time.

Bézier curve; polynomial; reparameterization; basis function; pyramid algorithm

TP 391.72

10.11996/JG.j.2095-302X.2020040576

A

2095-302X(2020)04-0576-07

2020-01-19；

2020-03-29

29 March，2020

19 January，2020；

国家自然科学基金项目(61772013)；中央高校基本科研业务费专项基金项目(JUSRP21816)

National Natural Science Foundation of China (61772013); Fundamental Research Funds for the Central Universities (JUSRP21816)

沈莞蔷(1981-)，女，江苏无锡人，副教授，博士，硕士生导师。主要研究方向为计算机辅助几何设计、计算机图形学等。E-mail：wq_shen@163.com

SHEN Wan-qiang (1981-), femal, associate professor, Ph.D. Her main research interest covers computer aided geometric design, computer graphics, etc. E-mail：wq_shen@163.com