王改霞,刘纪轩,李学志

(1.信阳学院数学与统计学院,河南 信阳464000;2.空军工程大学航空机务士官学校基础部,河南 信阳464000;3.河南师范大学数学与信息科学学院,河南 新乡453007)

1.引言

2017年10月27日,世界卫生组织国际癌症研究机构公布的致癌物清单初步整理参考,乙型肝炎病毒(慢性感染)在一类致癌物清单中.慢性乙型肝炎(简称乙肝)是指乙肝病毒检测为阳性,病程超过半年或发病日期不明确而临床有慢性肝炎表现者.临床表现为乏力、畏食、恶心、腹胀、肝区疼痛等症状.从肝炎病毒入侵到临床出现最初症状以前,这段时期称为潜伏期[1−4].乙肝潜伏期为6周～6个月,一般为3个月.潜伏期随病原体的种类、数量、毒力、人体免疫状态而长短不一.

因为不同年龄的人对乙肝的免疫能力、潜伏期长短、感染能力及传播能力不同,故年龄对乙肝传播的影响不可忽略[5−10].而不同体质的易感者接触乙肝病人后可能会直接发病,也可能潜伏一段时间才表现出来,因而讨论易感类人群接触病人后比例进入潜伏类和染病类的传染病模型更加符合实际.

2.模型

把总人口分为易感类、潜伏类、染病类、免疫类,分别用S(a,t),E(a,t),I(a,t),R(a,t)表示各类年龄密度函数,a为年龄,t为时间.µ(a)为年龄依赖自然死亡率,[ε(a)]−1平均潜伏周期,[α(a)]−1为平均染病周期,b(a)为年龄依赖出生率.令感染力函数[5]为

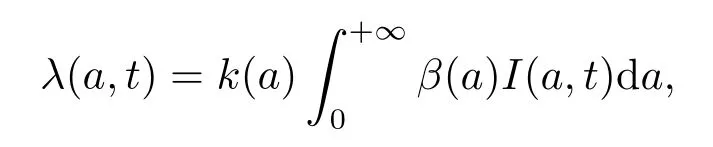
其中β(a)为年龄依赖的染病率,k(a)为年龄依赖的接触率.不考虑因病死亡,则易感类人群接触病人后按比例q和1−q进入潜伏类和染病类的年龄结构SEIR传染病模型为

这是一个标准的Mckendrick-von forester方程.假设所有的参数都非负,且

假设当个体超过一定生育年龄时b(a)=0.假设总人口处于稳定状态[6],即假设

设S0(a)≥0,E0(a)≥0,I0(a)≥0,R0(a)≥0,S0(a)+E0(a)+I0(a)+R0(a)=P∞(a).则有

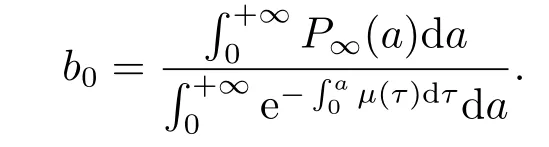
由(2.3)得

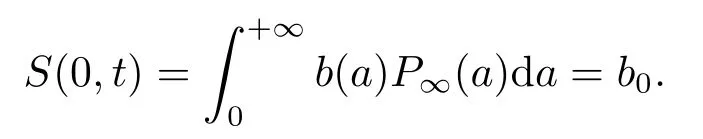
对系统(2.1) 作归一化处理

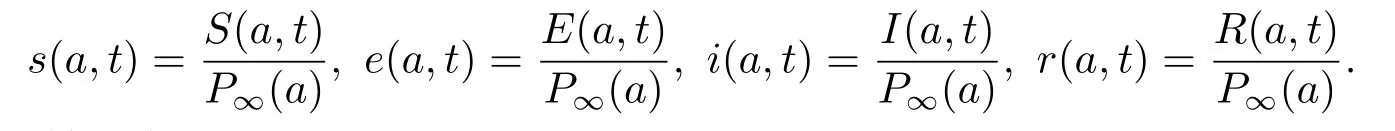
则系统(2.1) 转化为

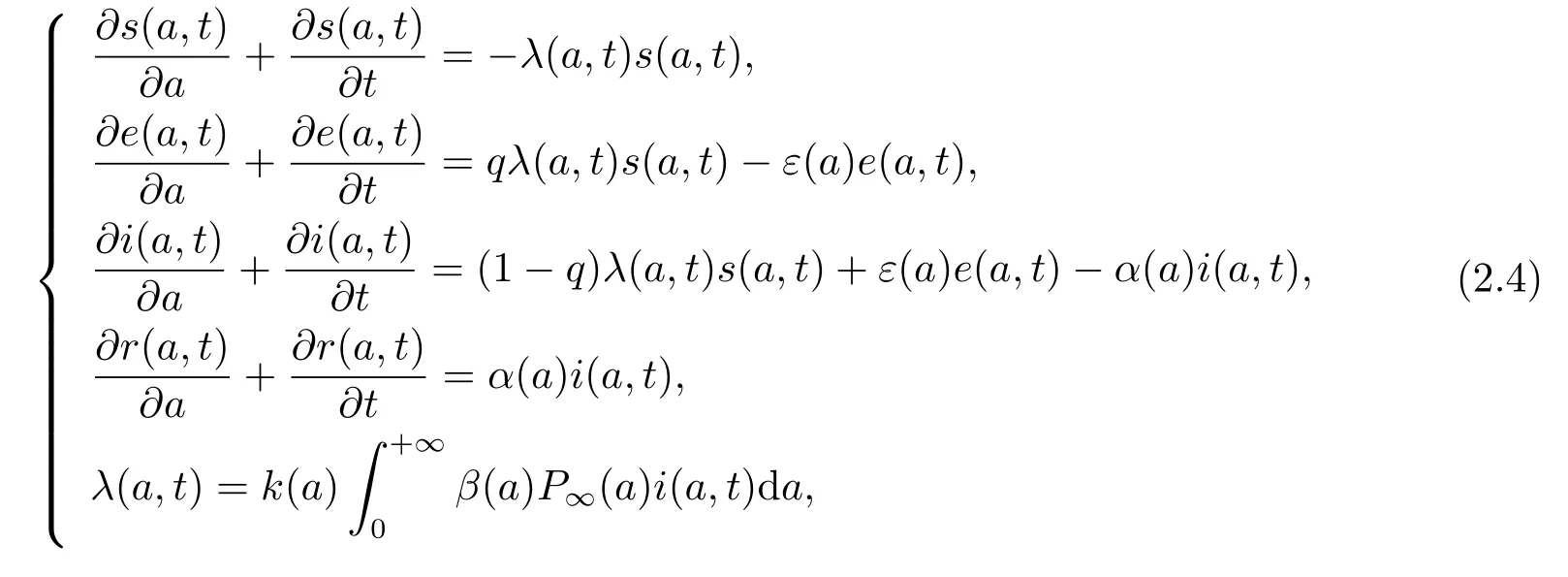
及边界条件

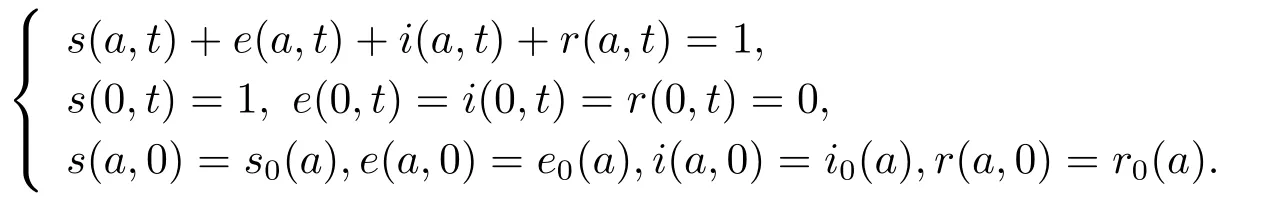
3.无病平衡点及其稳定性

系统(2.4) 及其边界条件的平衡解满足

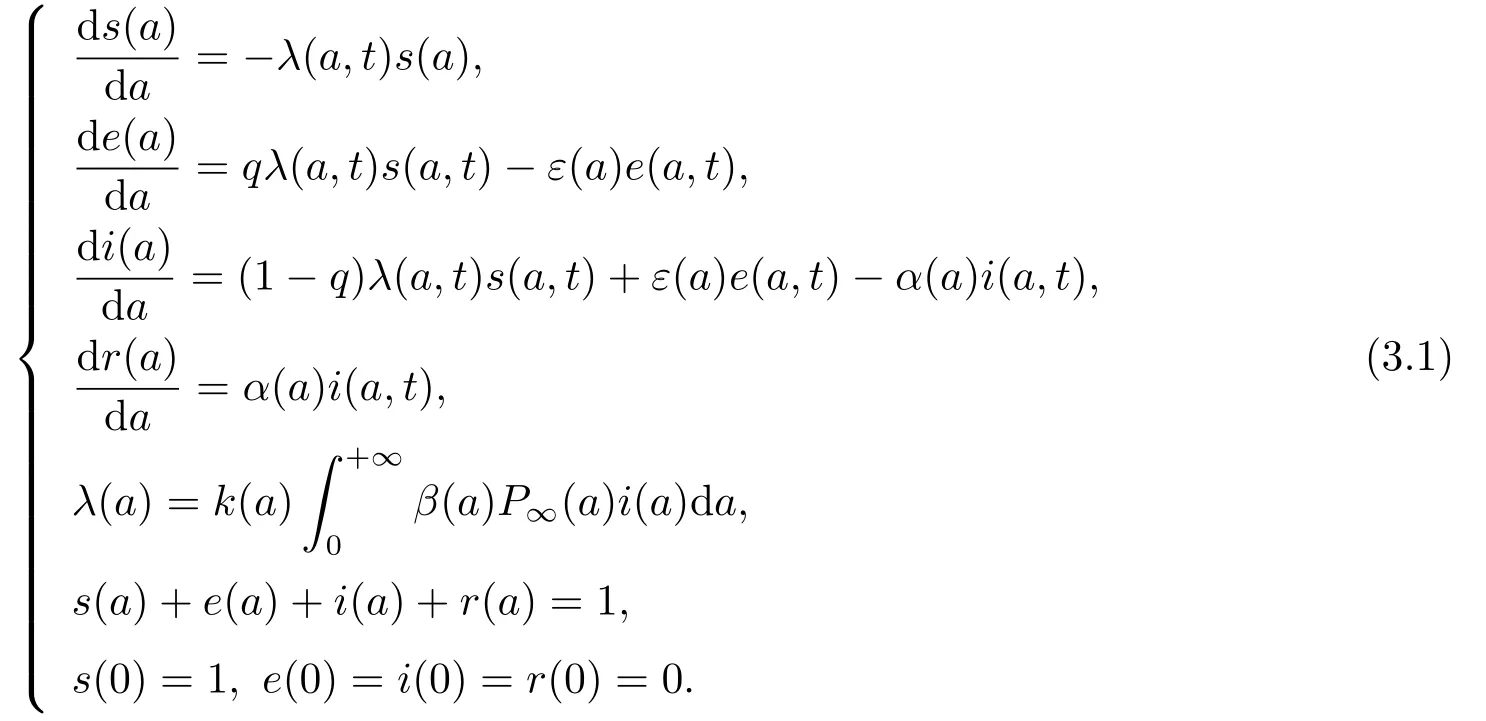
易得(3.1)的无病平衡点E0(1,0,0,0).为讨论其稳定性,将系统(2.4)在E0处线性化,考虑如下形式的指数解

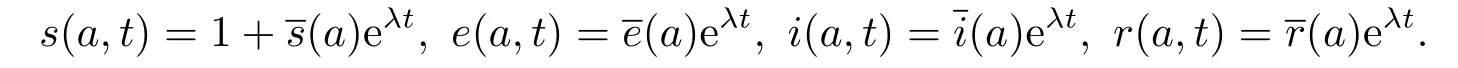
省略高阶项得

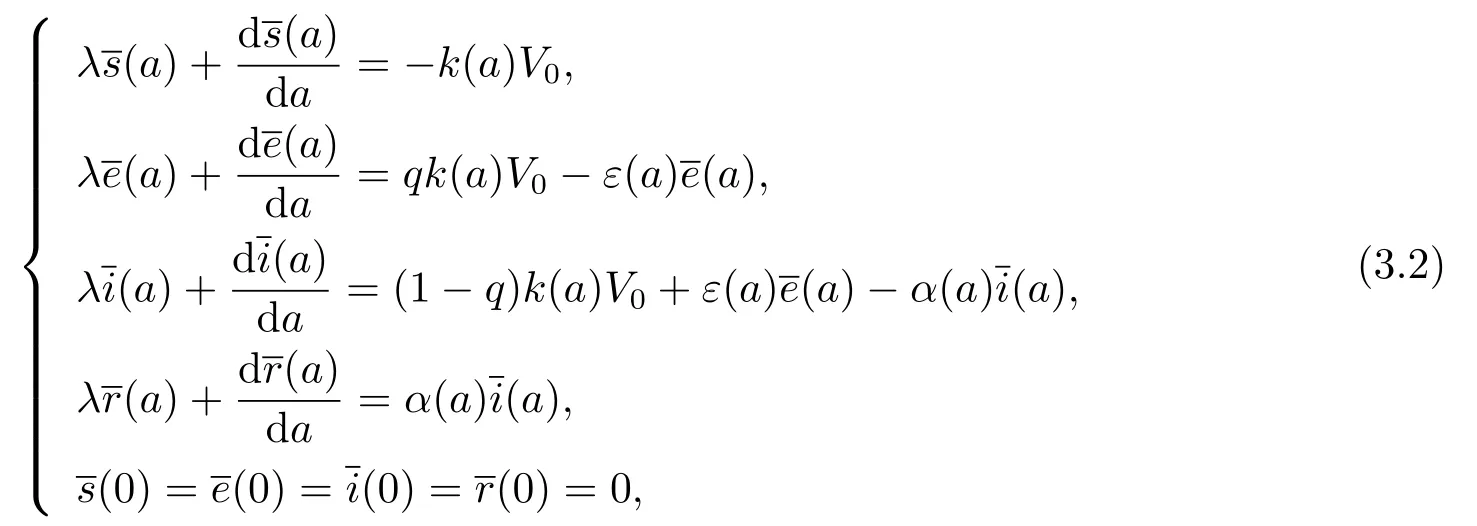
其中

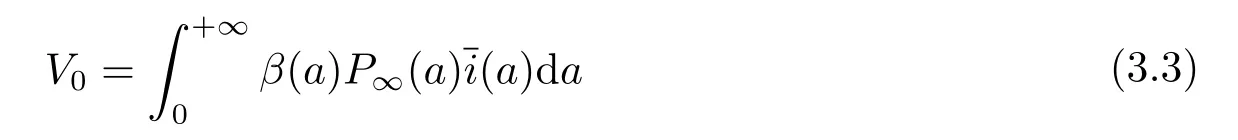
为常数.由(3.2)第二个方程得

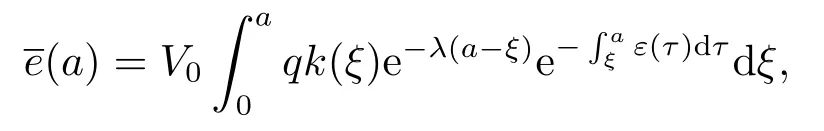
代入(3.2)第三个方程得

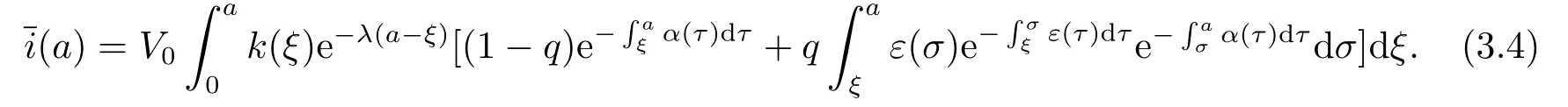
把(3.4)代入(3.3),两边同除以V0(其中V0≠0) 可得特征方程为

4.地方病平衡点的存在性和稳定性

其中N是总人口,β+=max{sup[0,+∞)β(a)}.

定理4.2若条件(4.9)满足,则

1)T(λ)关于λ递减且当λ →+∞时趋近于0;

2)T(0)<1.

证1) 若条件(4.9)满足,则(4.8)式两个中括号内的式子都大于零,进而可得T(λ)≥0,关于指数λ递减且当λ →+∞时T →0.

2) 令λ=0得

由(4.4)可以看出上式第一项积分等于1.因此,T(0)<1.证毕.

定理4.2及(4.8)说明方程T(λ)=1,也就是(4.7)有唯一的负实根且所有的复根实部都小于这个实根.因此有

定理4.3假设(4.9)成立,则系统(2.4)的地方病平衡点局部渐近稳定.

5.讨论