覃 华，刘 政，苏一丹

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

密度峰值聚类算法(DPC)具有计算效率高、能检测非球形簇等优点[1,2]，但该算法密度计算方法存在两大不足：一是密度计算所需的截断阈值dc依靠经验选取，造成算法对特征复杂的实际数据集辨识能力偏低；二是需要手动选取聚类中心，存在较大的人为误差。国内外文献对DPC的两大缺陷展开了相关研究，文献[3]提出用加权模糊K近邻方法解决截断阈值dc的选择标准问题；文献[4]引入势场模型自动选择截断阈值dc； 文献[5]用合并聚类中心方法实现自动选择截断阈值dc； 文献[6]用布谷鸟算法实现截断阈值dc的自动最优化选择；文献[7,8]用果蝇算法、DNA遗传算法优化截断阈值dc与聚类中心的选择问题；文献[9]提出用线性拟合方法自动选择聚类中心。

受上述文献启发，为避免截断阈值dc对密度计算的影响，本文提出一种最优密度估计方法计算DPC的密度，首先使用最优Oracle逼近[10]计算出最优化协方差矩阵，再利用最优协方差矩阵构造马氏距离，通过最优协方差矩阵提高DPC对数据相似度的区分能力，实现DPC中对数据样本密度的最优估计，最后通过K近邻算法计算出数据样本的密度，构造出基于最优密度估计的密度峰值聚类算法(density peaks clustering algorithm based on optimal density estimation)。人工数据集、UCI真实数据集上的仿真实验结果以及与其它DPC改进算法计算结果的比较验证了所提算法的可行性。

1 DPC的基本概念

密度峰值聚类算法基于两种假设：①聚类中心被比其密度小的点所包围。②密度中心离其它局部密度较大的点较远。基于上述假设，样本点的密度ρi和样本点与比其密度大且离其最近的点的距离δi被应用于聚类当中。样本点密度ρi的计算如下

(1)

当x<0时χ(x)=1， 当x≥0时χ(x)=0， 其中dc为截断距离，dij为点i与点j的样本相似度，通常为样本点间的欧式距离。密度ρi表示为以点i为中心，dc为半径的圆内的点的个数。在DPC算法的源代码中，作者提供了另一种ρi的计算方法

(2)

式(1)的使用可能会经常使一些样本点获得相同的密度，影响聚类中心的选择，式(2)使用高斯核来计算样本点的密度，在一定程度上解决了式(1)存在的问题。式(1)和式(2)中唯一参数dc的选择，影响着聚类的结果，原文建议取使以dc为半径的圆内包含的数据点为数据集总点数的2%的值[1]。

样本点与比其密度大且离其最近的点的距离δi的计算如下

(3)

对于密度最大的点

(4)

DPC使用上述两个变量构建ρ-δ决策图，将ρ和δ都较大的点选取成为聚类中心。然后把剩下的点分配到比其密度大且离其最近的已分配的点的所属簇。为了实现聚类中心个数的自动确定与选取，原算法使用变量

γi=ρiδi

(5)

并对γi进行降序排列，构建γ决策图，当ρi和δi都较大时,γi的值会更大，中心点离非中心点的γi值会更远，在γ决策图中会出现点的跳跃。使用启发式方法可以在γ决策图中确定聚类中心个数。

2 最优Oracle估计的马氏距离计算

马氏距离[11]作为协方差距离，与欧式距离不同的是，马氏距离考虑了数据的分布信息，测量的是样本点x在分布D下与样本点y相差的分布D的标准差的数量，分布D的信息体现在协方差矩阵S上，并且马氏距离是一种无量纲的计算方法，马氏距离的计算如下

(6)

其中，S-1为分布D的样本协方差矩阵的逆矩阵。S为对称矩阵，主对角线上的元素为分布D在各个维度上的方差。除主对角线元素外其它元素为样本点所处分布D各个维度之间的协方差，是在分布D上样本点的整体关系。计算马氏距离，重点在于协方差矩阵的计算，协方差矩阵的计算受所选分布D与计算方法影响。

对于协方差矩阵的计算，传统的样本协方差矩阵计算方法为

(7)

当样本维数p大于样本总数n时，上式计算得到的协方差矩阵不可逆。当p/n的结果小于1且不可忽略时，上式计算协方差矩阵在进行求逆运算后得到的结果会有很大的估计误差，得到的协方差矩阵不是良好的。

(8)

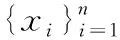
假设所有的xi都是无关系的并且有相等的方差，则协方差矩阵的一种直观估计为

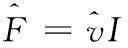
(9)

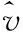
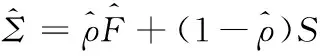
(10)

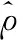
综上所述，想要得到一个良好的正定可逆的协方差矩阵的估计，需要满足下述条件

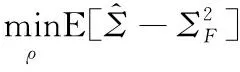
(11)

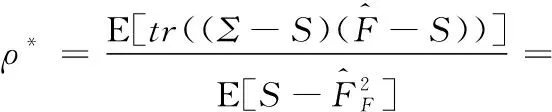
(12)

其中，ρ*的最佳取值区间为[0,1]，将ρ*代入式(10)得到协方差的Oracle估计，然而在大多数情况下Σ是未知的，ρ*不能得到结果，只能对其进行逼近。

OAS是Oracle估计的一种最佳逼近方法，OAS预先对Σ进行假设，然后循环迭代这个假设直到收敛，最后得到的ρ*的近似值为

(13)

将上式代入式(10)得到最优协方差矩阵

(14)

使用上式计算马氏距离得最优Oracle估计的马氏距离(OAS马氏距离)

(15)

使用最优Oracle估计计算马氏距离中的协方差矩阵，可以提升马氏距离在维数高的数据集的适用性和相似度的区分能力，减小计算误差。

3 基于最优密度估计的密度峰值聚类算法

本文提出算法的基本思想为：使用样本点的K个近邻点作为分布计算样本点与其K个近邻点的OAS马氏距离，并用于样本点密度的计算。

设X=[x1,x2,…,xN]， 为N个样本， NNk(xi) 为在欧式距离下，离xi最近的第K个样本点，xi的K近邻点定义如下

KNN(xi)={j∈X|d(xi,xj)≤d(xi,NNk(xi))}

(16)

基于OAS马氏距离的K近邻样本密度

(17)

其中，ρi为使用样本点xi的K个近邻点作为分布D计算该点与其最近K个点的马氏距离并求和。K取值与dc类似，可以为总点数的一个百分比。对ρi进行进一步改进，对边界点进行惩罚，得到最优密度估计方法为

(18)

上式中的第三项为惩罚项，用于使聚类中心的选取远离边界点，ω为惩罚系数，使用上式最优密度估计方法，可以提高DPC对数据相似度的区分能力，使密度计算不受数据量纲影响，提升聚类精度。

所提算法流程如下：

输入：数据集X=[x1,x2,…,xN]，k、ω值。

输出：数据集中样本标签class。

步骤1 计算样本点间的欧式距离dij。

步骤3 使用式(3)和式(4)计算样本点的δi。

步骤4 使用式(5)计算样本点的γi， 并建立γ决策图，获取聚类中心数目。

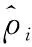
步骤6 将剩余未分配的点，按照原DPC算法对聚类中心以外的点的分配方式进行分配[1]。

上述算法中，关键点是根据最优密度估计建立决策图并确定聚类中心，以下通过与原始DPC方法相比较，说明所提算法确定聚类中心的优点。

图1为使用DPC算法在随机生成的多密度数据集上的聚类中心选取结果，实心点为被选取为聚类中心的点。从图中可以看出，密集程度较小的棱形簇在DPC算法的密度计算方式下，拥有较小的密度，在ρ-δ决策图上贴近于δ轴，不能被选取为簇中心，导致簇中心选取错误。

图1 DPC聚类中心选取结果

图2为使用本文算法在与图1相同数据集上的聚类中心选取结果，实心点为被选取为聚类中心的点。从图中可以看出，密集程度较小的棱形簇在本文算法的密度计算方式下，也能拥有相对较大的密度，从而能从决策图中被选取为簇中心，并且中心点离其它非中心点在ρ-δ决策图中的距离较远，便于簇中心的选取。

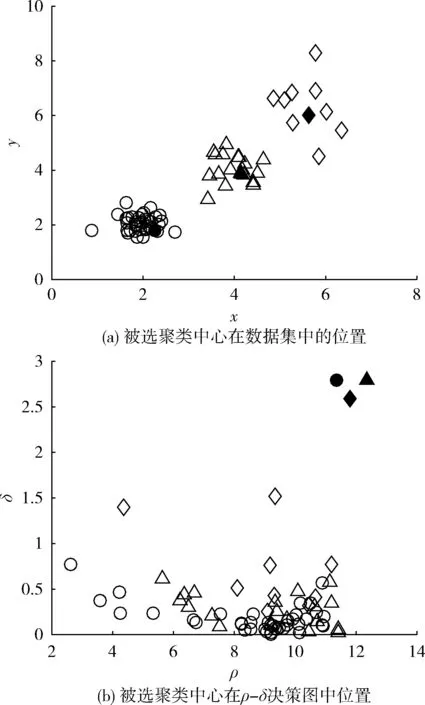
图2 本文算法聚类中心选取结果

4 仿真实验

在人工数据集和UCI真实数据集上检验所提算法的聚类效果和性能，实验的硬件环境为Intel Core i7-6700HQ @2.6 Hz CPU, 16 GB内存，在Windows7 x64平台上用Matlab2016a实现算法。

4.1 实验数据集说明

实验用到4个人工数据集和8个UCI真实数据集，数据集的描述详见表1和表2。

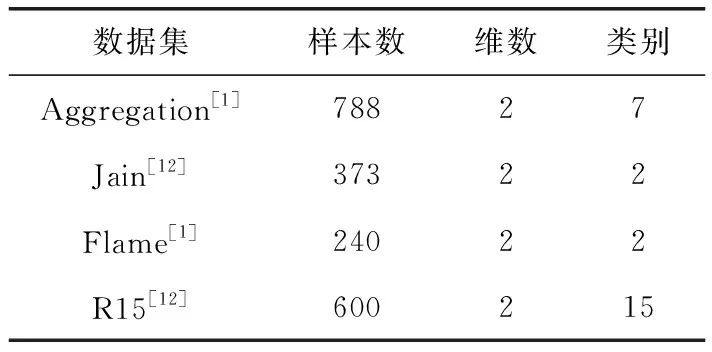
表1 人工数据集信息

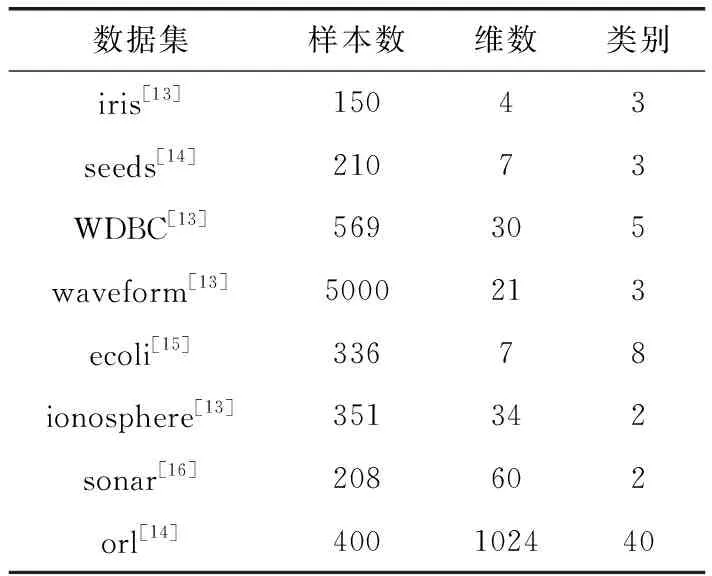
表2 UCI真实数据集信息

4.2 实验结果与分析

(1)人工数据集上的实验结果及分析

本文算法与DPC算法[1]在人工数据集上的实验结果比较如图3～图6所示，被分为同一簇的样本点在图中拥有相同的形状和灰度。DPC算法在Aggregation、Flame、R15、Jain数据集上的dc设置分别为2%、3%、2%、1%[1]。本文算法在Aggregation和Flame数据集上的参数设置为k为2，ω为3，在R15和Jain数据集上的参数设置为k为3，ω为3[11]。

图3 Jain数据集聚类结果对比

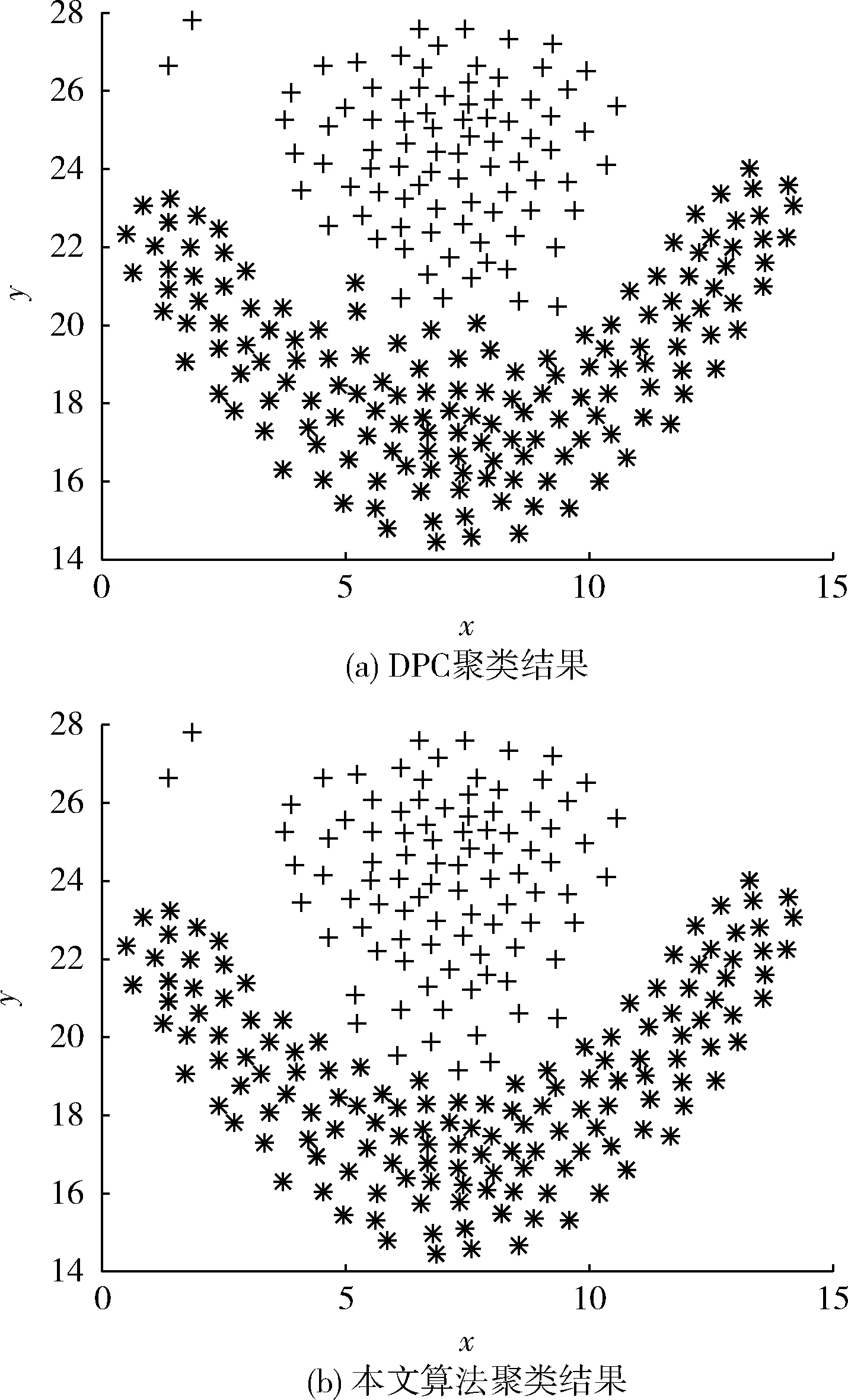
图4 Flame数据集聚类结果对比

图5 R15数据集聚类结果对比

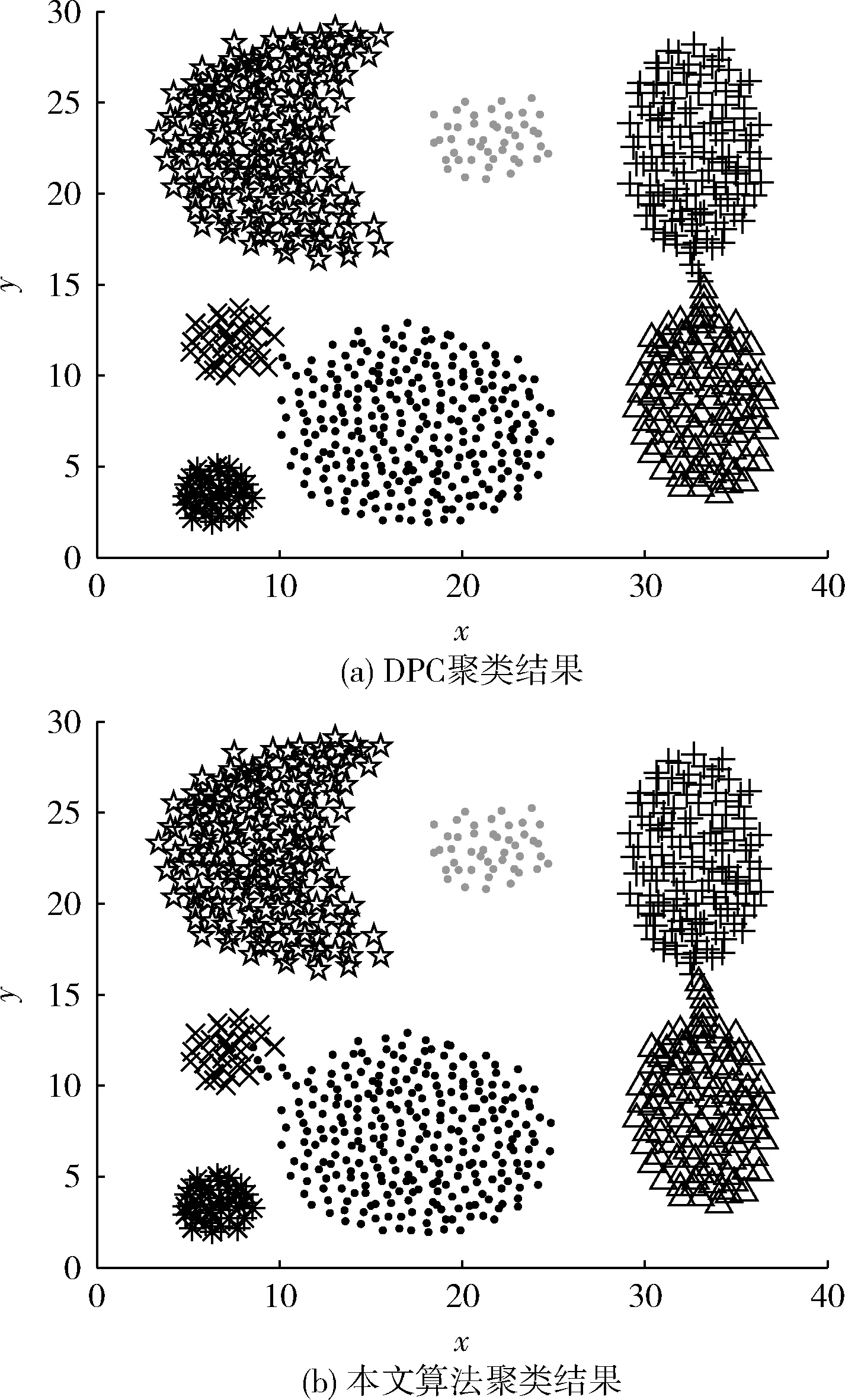
图6 Aggregation数据集聚类结果对比

图3的聚类结果显示，在有两个不同密度簇的数据集Jain上，DPC错误的将密集程度相对较高的簇的样本点选为密集程度相对较低的簇的中心，导致聚类结果不理想。而本文算法能够正确找出不同密度簇的簇中心，并正确的对剩余点进行分配，得到正确的聚类结果。

图4的聚类结果显示，在有两个不同形状簇的Flame数据集上，原DPC算法与本文算法都能识别两个不同形状的簇。对比原DPC算法，本文算法在簇的连接处识别率与原算法相当差异较小，亦保持着较高的准确率。

图5是DPC算法与本文算法在拥有多个簇的R15数据集上的比较。由图可知，两种算法都能够识别其中的15个簇，并且识别正确率相当。

图6是Aggregation典型团状数据集两种算法计算结果的比较，由图可看出两种算法均能准确地识别出7个簇,聚类表现差距较小,聚类精确率相当。

从上述实验结果比较可看出，本文算法和DPC算法在有特定形状的人工数据集上聚类效果相当，说明原始DPC算法对有特定形状的人工数据集本身就有较强的判断、识别能力，本文改进后聚类精度提高不明显。

(2)在UCI真实数据集上的实验结果及分析

在UCI真实数据集上，将本文所提算法与原DPC[1]算法及近年其它的改进DPC算法CDP[14]算法和FN-DP[13]算法相比较，结果采用准确率(accuracy，ACC)[14]、标准化互信息(normalized mutual information，NMI)[14]指标进行评估，两个指标的取值范围均为[0,1]，取值越大，表示得到的聚类结果越好。实验结果对比详见表3和表4，两表中的符号“-”表示相应文献未给出该数据集的计算结果，无法在此数据集进行结果比较。

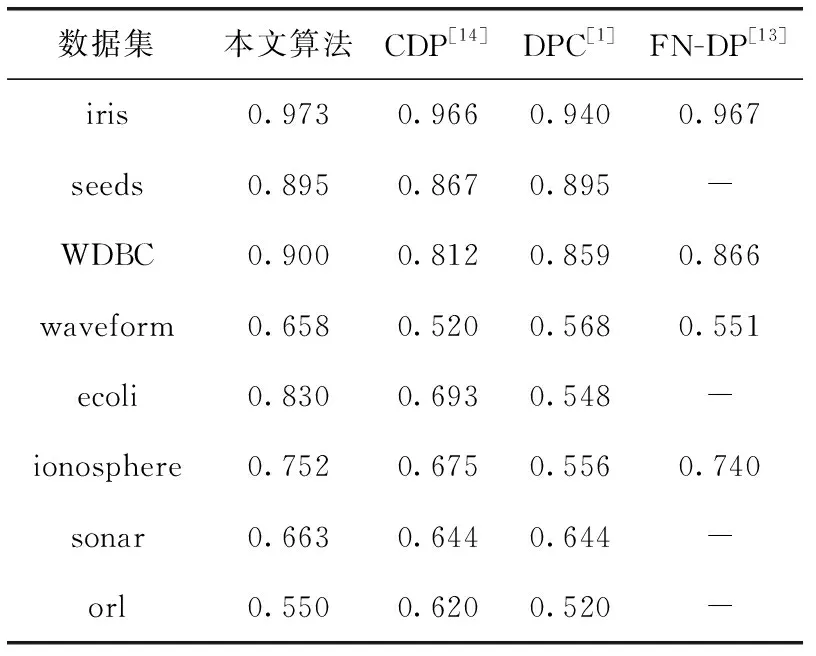
表3 各算法聚类准确率(ACC)对比

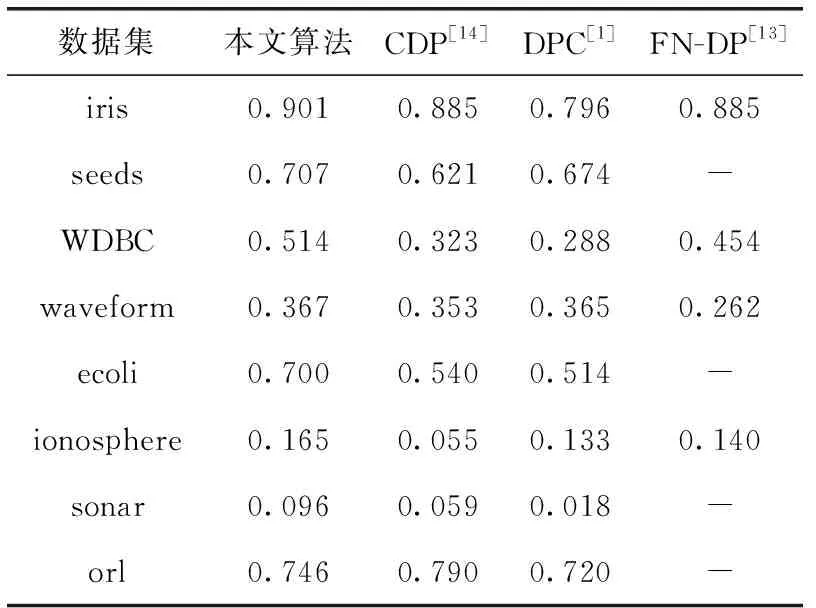
表4 各算法标准化互信息值(NMI)对比

从表3和表4的实验结果对比得出。在iris数据集上对比原DPC算法与CDP算法和FN-DP算法，本文算法在两个评估指标上获得了较好的结果。本文算法较原DPC算法在准确率上提高3.3%，较CDP算法提高0.7%，较 FN-DP 算法提高0.6%。在标准化互信息上较原DPC算法提高10.5%，较CDP算法提高1.6%，较FN-DP算法提高1.6%。FN-DP算法使用模糊逻辑原理，使样本点的局部密度更能反映局部信息，而本文算法使用KNN马氏距离能使样本点的局部密度能更好反映局部信息。

在seeds数据集的实验结果显示，本文算法在两个指标上优于原DPC算法和CDP算法。本文算法较原DPC算法在准确率上相等，较CDP算法提高2.8%。在标准化互信息上较原DPC算法提高3.3%，较CDP算法提高8.6%。

在乳腺癌数据集WDBC的实验结果显示，本文算法在两个指标上的都优于原DPC算法与CDP算法及FN-DP算法。本文算法较原DPC算法在准确率上提高了4.1%，较CDP算法提高8.8%，较FN-DP算法提高3.4%。在标准化互信息上较原DPC算法提高22.6%，较CDP算法提高19.1%，较FN-DP算法提高6%。

在样本数目较大的数据集waveform的实验结果显示，本文算法在两个指标上都优于原DPC算法与CDP算法及FN-DP算法。本文算法较原DPC算法在准确率上提高9%，较CDP算法提高13.8%，较FN-DP算法提高10.7%。在标准化互信息上较原DPC算法提高0.2%，较CDP提高1.4%，较FN-DP算法提高10.5%。

在大肠杆菌数据集ecoli的实验结果显示，本文的算法在两个指标上都优于原算法与CDP算法。本文算法较原DPC算法在准确率上提高28.2%，较CDP算法提高13.7%。在标准化互信息上较原DPC算法提高18.6%，较CDP算法提高16%。

在特征数较多的雷达数据集ionosphere上的实验结果显示，本文的算法在两个指标上都优于原DPC算法与CDP算法及FN-DP算法。本文算法较原DPC算法在准确率上提高19.6%，较CDP算法提高7.7%，较FN-DP算法提高1.2%。在标准化互信息上较原DPC算法提高3.2%，较CDP算法提高11%，较FN-DP算法提高2.5%。

在sonar数据集上的实验结果显示，本文的算法在两个指标上都优于原DPC算法与CDP算法。本文算法较原DPC算法在准确率上提高1.9%，较CDP算法提高1.9%。在标准化互信息上较原DPC算法提高7.8%，较CDP算法提高3.7%。

人脸数据集orl为样本维度较高的数据集，在orl数据集上的实验结果显示，本文算法在两个指标上的表现低于CDP算法，高于原DPC算法。本文算法较原DPC算法在准确率上提高3%，较CDP算法低7%。在标准化互信息上较原DPC算法提高2.6%，较CDP算法低4.4%。

从上述实际数据集的计算结果比较可看出，对于特征复杂的实际数据集，本文引入式(14)的最优协方差矩阵用于描述数据集不同维度(特征变量)间的相关性，并在式(6)计算样本相似度时考虑了各特征维度的重要程度，式(18)利用此相似度计算样本的密度值后，通过计算出的密度值能更容易判别样本的归属簇，例如在waveform、ionosphere、ecoli数据集上，本文算法能够在密度不一的簇中寻找到合适的簇中心，并使非中心点能够更正确地进行分配，进而提高了DPC的聚类精度。

综述上所述，本文引入最优密度估计改进DPC的密度计算后，所提算法在UCI真实数据集上优于相比较的其它DPC改进算法，因此本文改进DPC的思路是可行的、有效的。

5 结束语

传统的DPC算法的密度计算存在dc参数优化等缺陷，造成算法对没有特定形状的实际数据集聚类精度欠佳，针对此问题，本文利用Oracle最优逼近估计和K近邻算法计算数据样本的密度，避免了截断阈值dc取值对密度计算的不良影响，从而提高了DPC对实际数据集的特征辨识能力，提高了算法的聚类精度。在UCI真实数据集上的实验结果显示，本文算法能够有效地提高DPC的聚类精度，具有良好的适用性。综上所述，所提改进DPC的思路是可行的。