基于供应链视角的农产品物流成本控制模型分析
2020-07-06刘艳萍


【摘要】 新时代中国物流业发展愿景为促进农产品物流增长带来良好契机,与供应链管理理论极大推动农产品物流朝着横向一体化发展,形成的双重背景下,降低物流成本成为农产品物流竞争的突破点。文章在论述农产品供应链物流理论及农产品物流供应链成本的基础上提出供应链视角下,从库存持有成本、订单处理成本、缺货成本和运输成本分类模型中分析农产品供应链物流成本模型的构建;同时依据事前交易成本和事后交易成本对农产品供应链交易成本模型的构建加以分析。
【关键词】 农产品物流;供应链物流成本;供应链交易成本
【中图分类号】 F234 【文献标识码】 A 【文章编号】 1002-5812(2020)11-0070-04
一、引言
党的十九大报告提出,新时代中国发展方略对物流业发展提出新要求,现代供应链成为物流业发展的新动能,未来物流业将进入以质量和效益提升为核心的新发展阶段。农产品物流是实现农业生产资料流转和农产品流通的必要手段,中国作为农产品生产、消费和贸易大国,大力发展农产品物流,对于提升农村一二三产业融合发展水平,助力乡村振兴战略有着深远影响。
中国农产品流通成本一般占总成本的40%左右,其中鲜活产品及果蔬产品要占到60%以上,而国外发达国家物流成本一般控制在10%左右。国务院2017年发布的《关于积极推进供应链创新与应用的指导意见》将加速中国进入经济转型发展的供应链创新时代。为此,物流成本管理随着供应链管理思想的产生和国家战略发展的需要而迈入物流供应链成本管理阶段。
二、文献综述
张珊与王蓉(2011)将物流成本控制范围从企业内部扩大到整个产业供应链的物流运作过程,并以现代企业间竞争转变为供应链间竞争为背景提出供应链成本理论概念与逻辑框架。辜明华(2019)利用大数据技术解决采购、销售、库存等企业内部物流供应链环节成本控制问题。杨志宏等(2011)针对蔬菜供应链各环节的成本进行分析,提出降低流通费用及最终促进农产品超市经营发展的解决思路。郭玉杰(2014)和梁瑞智(2018)把作为社会物流体系中的农产品物流的成本按照广义和狭义分类,并以农产品加工配送企业对农产品物流成本制约的影响因素和控制策略进行了研究。章艳华(2017)研究得出生鲜农产品深加工规模能够有效提升供应链整体及各盟员的收益水平的结论。本文将以供应链视角对农产品物流成本控制模型进行深入分析。
三、农产品供应链物流理论分析
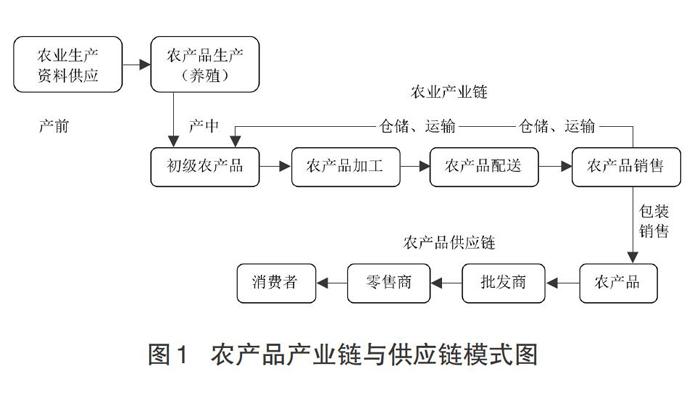
在农产品产业链的相同领域中以农产品流通与消费为主要研究对象便形成农产品供应链(如图1所示)。农产品供应链不仅包括农产品加工企业和生产者,还包括运输商、批发商、零售商和最终消费者等所有链上成员;亦是围绕核心企业对农产品从生产到消费过程中的各个环节涉及到的物流、商流、信息流和资金流进行的整合体;其目的是采用集成化管理方法满足消费者需求,即有效满足客户需要的功能系统,并实现整体上的高效益和低成本。这样,企业之间的竞争就转变为供应链间的竞争。
农产品物流是农产品供应链的重要组成部分,是商品流通的过程管理,只有在商品流通中才会使商贸、信息、资金得以完成或实现。供应链指导下的物流不仅表现为极大的集成化优势,且还可以构建合理的物流路径和结点,在全面提升物流运作效率的同时节约交易费用、降低物流成本,使农产品从田间到餐桌最终满足农产品消费者需求并获得供应链的整体利益,也称为农产品供应链物流。提高农产品物流水平,减少农产品供应链环节的同时,可以通过控制农产品物流成本进而减少农产品供应链总成本。
四、农产品物流供应链成本分析
依据德国学者StefanSeuring提出供应链成本可划分为直接成本、作业成本、交易成本,鲍新中将生鲜农产品供应链成本划分为作业成本、损耗成本和交易成本三种。共同都含作业成本和交易成本外,直接成本是农产品物流的单个企业里,经过或生产加工、或运输、或仓储等功能产生的运作成本,而损耗成本是由于生鲜农产品在流通过程中消耗的并随时间延长而成倍递增的损失,且超过保鲜期后的农产品就彻底失去自身价值,这必然成为需要各个功能企业自行承担的直接成本。
本文将农产品物流按照作业进行划分并探讨其成本动因选取。运行不同物流功能的企业将物流职能划分为不同作业进行核算与管理,仓储成本、运输成本、装卸成本、加工包装成本等均产生于物流职能的履行,所以将作业成本归为物流成本中进行管理。同样,直接成本也是农产品流通中履行各个物流功能的企业自行承担的成本,应同属于物流成本管理范围。
农产品供应链交易成本是横向一体化管理模式中必然发生的企业间交往、合作等发生交易而消耗的物化劳动和活劳动的成本。科斯同样也将交易成本分为交易前、交易中及交易后的成本。考虑生鲜农产品交易的特点,农产品供应链交易成本不仅包括交易谈判成本、合同签约成本和信息获取成本等,还包括了农产品在等待交易时发生的保管人员成本、场所使用成本、存储管理成本和交易中产生的损耗成本等,且等待时间越长,不确定可能越大,交易成本也越高。为此,本文将探讨的农产品物流供应链成本分为物流成本和交易成本两大类(如图2所示)。
五、农产品供应链物流成本模型
国内外学者均对供应链物流成本及其管理进行了建模研究。随着互联网技术迅猛发展,研究对象已由供应链内部转向外部,促使供应链成本研究更注重时间因素的影响,研究的焦点多集中在库存、运输配送方面。
(一)库存持有成本模型构建。描述库存成本模型为CH=[0Qhtndq]或者CH=[0thtndq=hQn+αn+αD-θQn+2αn+2αD2],此时Q是订货量,q(t)是t(0≤t≤1)时刻的库存水平,在有α和β作为状态参数时衡量需求率对现有库存水平变化的敏感性。q(t)在周期时间T内的即时状态下可通过下列一阶非线性微分方程給出:
[dqtdt+θqt=-Dqtβ]
(二)订单处理成本模型构建。由传统订货量模型(EOQ)取得每次订货成本为固定常数,延伸为固定订货成本(K)与可变订货成本(C)组成。在库存控制策略为最大库存水平取向时,界定n期的订货总成本为:
[C0=t-1n][Kδ(St-Xt)+C·(St-Xt)]
其中Xt代表第t期的期初库存量,St代表最大库存水平,而[δt](St-Xt)代表是否订货的可能性0—1变量。
如果针对EDI订货环境假设购买方订货成本Ti(K)是单位时间订货系统投资费用的指数函数。其模型为:
Ti(K)=[Ti]([T0ie-rk]),[r>0],i=1,2,…,m
假设KSP为农产品采购的时间成本,KSR为订单验收成本,假设农产品物流采购人力资本空闲率为[α],库存控制策略为(R,Q)策略,则订单成本为:
C0=([DQ])·[αKsp+(1-α)Ksp]
(三)缺货成本模型构建。通过将报童模型加入期末残值(S)与缺货成本(W)后,报童模型得以扩展为:
如果假設P+Q>S,且上述模式一阶偏导为零,则满足:F(Q*)=(P-C+B)/(P-S+B),如若库存不足,有成本Cμ=P-C+B,而如果库存过剩,有成本C0=C-B,则最优订货批量为:F(Q*)=Cμ/(Cμ+C0)。
(四)运输成本模型构建。供应链管理视角下,运输成本成为总成本函数中不可缺少的内容,如果将运输成本设为固定运输成本Cf和可变运输成本Cv,则有CT=Cf+Cv·D。当运输中仅与距离有关时,可将Cf和Cv设为距离的函数,即有Cf=Cs+Cd·d和Cv=C′s+C′d·d,此时的Cs代表每次运输中发生的固定成本,Cd代表单位车辆运行一公里所耗费的成本,C′s代表运输一件单独产品的附加成本,C′d代表着每件农产品每运行一公里的边际磨损和运行成本。
为使现实中较好拟合运输费率,将运输成本扩展为幂函数:令CT=f(Q)·D·(W/100)=a(QW)b·(1-d)·D·(W/100)。其中,f(Q)是幂函数形式的运输价格函数。在实际农产品满载时,满载运输的运价费率可以单位里程为基础计算,单位农产品运价费率是随着运载量上升而下降的。此时一般运输成本模型:CT=f(Q)·D=(Fx·Wx/Qw)·D·W。如果假设考虑运价折扣为d,则运输函数可变换为:CT=f(Q)·D=[Fx+d·Fx·(Wx-Qw)/Qw]·D·W。
六、农产品供应链交易成本模型
(一)事前交易成本分析模型。农产品供应链各节点企业间进行交易而产生的事前交易成本,企业可以从现有数据中获取,并按照作业动因进行分析、确认与计量。从供应链层面上分析成本发生的动因,通过动因分配费用,促进企业寻找出不增值但消耗资源的作业,尽可能增加增值作业,消除或减少不增值作业,进而有效达到控制供应链交易事前成本促使供应链效益最优的目标,是基于作业成本模型而展开分析的。
处于农产品供应链上的企业为达到m个交易行为,需要n种交易活动,s种资源,并假设BC为事前交易成本,Q为达成交易前所有耗费的交易活动数量,R为单位交易活动所消耗的资源量,p为所消耗的单位资源价格。农产品供应链上企业在达成交易前发生的成本有前期资源搜集成本、谈判成本与签约成本,如果假设基于作业成本的事前交易成本公式为:BC=QmnRnsP,而消除交易层面上不增值交易活动后事前交易成本控制模型为:BC=Qm(n-1)R(n-1)sP,优化供应链交易可以随着农产品供应链节点企业间的信任程度而变化,以此达到实现交易各方共赢的目标。
(二)事后交易成本分析模型。农产品物流在供应链模式下运用委托代理理论,考虑到环境中的复杂性与非确定性,包括了供应链参与主体之间的利益冲突和信息不确定性,来进行供应链事后交易成本的分析。
1.模型假设分析。将供应链上游企业假设为委托方,将下游节点企业假设为受托方即代理人。委托方得到的农产品价值用y=rk+ε表示时,r为受托方的努力程度,k为专用资产的投资影响系数,ε代表外部风险,其概率分布为正态分布且有E(ε)=0,Var(ε)=σ2。ε代表不可控的影响下游供应链企业农产品价值的事件。其期望产出为:E(y)=E(rk+ε)=rk,Var(y)=σ2。
作为农产品供应链上游企业的委托人对下游企业代理人的激励函数设为ω(y)=s+by,通过支付方式来调节和实现委托人对代理人的激励影响。此时,s代表与产品价值没有关系的固定额支付,b是代理方分享的委托方农产品价值的份额,代表了委托人与代理人的风险划分程度。将代理人的成本函数设为c(r)=[λ2]r2,λ为成本系数,r为努力程度。当λ>0表示相同努力带来的不同的负效用,得出实际收入函数为χ=ω(y)-c(r)=s+b(rk+ε)-[λ2]r2。这也说明,代理人的收入与代理人的努力程度、资产专用性投资、外部性风险以及委托人与代理人之间的风险划分是有很大的关系。
假定上游企业具有不变的绝对风险规避特征的效用函数,即μ=-e-ρx,确定性收入是实际收入的均值减去风险成本形成了如下函数:
E(χ)-[12]ρb2σ2=s+brk-[λ2]r2-[12]ρb2σ2
E(χ)代表上游企业的期望收入,[12]ρb2σ2是上游企业的风险成本,当b=0时,风险成本为零。上游企业最大化期望效用函数等价于最大化上述的确定性收入。如果令χ0为上游农产品企业保留的收入水平,而当上游企业从合同中得到的最大期望效用不能小于不接受合同时能得到的最大期望效用,可以如下模型表述(IR):s+brk-[λ2]r2-[12]ρb2σ2≥χ0。
2.模型构建分析。首先,考虑到下游的农产品企业能通过上游企业提供的产品与服务了解到其努力水平r,且在信息完全对称的条件下,对于最优的激励合同和激励约束(IC)不起作用,任何努力水平下的r都可以通过满足参与约束的(IR)强制合同来实现,因此上游企业委托人的问题变成选择(s,b)和r解最优化问题:
同时在成本最优的情况下,参与的约束等式如果成立,下游的单位企业就没有必要支付给上游企业更多代价来进行激励了。为此,参与约束通过固定项s构建目标函数为:
maxEv=-s+(1-b)rk=rk-[λ2]r2-[12]ρb2σ2-χ0
由于χ0是给定的,上述模型就意味着上游企业委托人实际是在最大化确定性等价收入减去努力水平后的成本,其最优化的一阶条件为:k-λr=0,此时得到最优解:
这个帕累托最优合同因为下游企业代理方是风险中等的,而上游企业是能够风险规避的,形成的以帕累托最优风险的分担要求上游单位企业不用承担任何风险(即b*=0),下游代理企业支付给上游委托企业的固定收入正好等于上游委托企业保留收入加上自身努力成本,所以上游委托企业的最优选择是r*=k/λ。
其次,考虑下游企业代理人倘若不能清楚了解上游企业委托人的努力水平r,只能从获得的产品价值及市场走势来判断,由此产生了需要考虑的上游单位企业委托人风险问题。从代理人企业视角设定努力程度r=b/λ,该努力程度受到企业的风险分担和工作难易程度的影响。如果下游代理人企业的风险分担的份额越大,则该企业自身付出的努力程度就越高,但如果代理人工作的难度越大,则努力程度越低。至此,上游委托人的最大化目标仍然是:
maxEv=max[-s+(1-b)rk]
s.t.[(IR):s+brk-λ2r2-12ρb2σ2≥χ0(IC):r=bλ]
将上述参与约束(IR)和激励约束(IC)都代入目标函数,使得最优化问题可以重新表达为:
[maxs,b]=[maxb][bkλ-12ρb2σ2-λ2bλ2-χ0]
边界条件为:[kλ]-[ρbσ2]-[bλ=0],即:b=[k1+λbσ2]。
上述模型存在着两类信息不对称下的代理成本,一类是由帕累托最优风险分担无法实现而产生的风险成本;另一类是由企业较低努力水平所导致的期望产出的净损失减去努力成本得到的节约额,被称为激励成本。因为下游代理企业是风险中等的,其努力水平可观测,促使上游企业承担全部风险意味着下游企业风险成本为零。当下游代理企业不能清楚了解其上游企业努力水平时,下游代理人承担的风险为:
b=[k1+λbσ2]
风险成本则为:
[ΔRC=][12][ρb2σ2=ρσ2k221+λpσ22]
同理,期望产出的净损失为:
[ΔEy]=[Δrk=][r*k-rk=][k2λ-k2λ1+λpσ22]=[ρσ2k21+λpσ2]
努力成本的节约:
[ΔC]=C[α*]-C[α=k22λ-k22λ1+λpσ22=2ρσ2+λpσ2221+λpσ22][k2]
所以得到的激励成本为:
[ΔEy]-[ΔC=ρσ2k21+λpσ2-2ρσ2+λpσ2221+λpσ22k2=λpkσ2221+λpσ22]
那么事后交易成本為:
AC=[ΔRC]+[ΔEy-ΔC=pσ2k221+λpσ22]+[λpkσ2221+λpσ22=]
最后,因为事后交易成本呈现出随着上游代理企业风险规避度ρ、产出的方差σ2和专用资产投资影响系数k的上升而上升。农产品供应链节点企业两两之间的事后交易成本能够计算出来,现在需要把整个农产品供应链各个节点企业的事后交易成本整合为供应链事后交易成本模型:
[i=1i=αAC]=[i=1i=αpiσ2ik2i21+λipiσ2i](α为供应链节点数)
至此得出供应链全部交易成本等于事前交易成本与事后交易成本之和,即:
TC=BC+[i=1αAC=Qm(n=1)]·[Q(n=1)s]·P+[i=1i=αpiσ2ik2i21+λipiσ2i]
七、结语
农产品供应链物流成本控制模型分析涵盖库存持有成本、订单处理成本、缺货成本和运输成本模型的构建分析。农产品物流企业进行有效供应链交易成本管控,可以运用作业成本模型和委托代理理论,从农产品供应链事前与事后两个方面产生的交易成本进行建模研究。
【主要参考文献】
[ 1 ] 张珊,章文芳,陆洲.基于供应链的物流成本管理探析[J].财会通讯,2011,(02):136-137.
[ 2 ] 王蓉,陈良华.供应链成本理论(SCC)演进框架解析与中国应用展望[J].东南大学学报(哲学社会科学版),2011,13(01):28-32+123.
[ 3 ] 辜明华.基于大数据的内部供应链成本控制策略探究[J].财会通讯,2019,(23):91-95.
[ 4 ] 杨志宏,翟印礼.超市农产品供应链流通成本分析——以沈阳市蔬菜市场为例[J].农业经济问题,2011,32(02):73-78+112.
[ 5 ] 郭玉杰.农产品物流成本控制因素分析[J].财会通讯,2014,(11):100-102.
[ 6 ] 梁瑞智.农产品加工配送企业物流成本控制研究——以M公司为例[J].商业会计,2018,(08):38-40.
[ 7 ] 章艳华.基于供应链契约的生鲜农产品深加工企业决策探析[J].财会月刊,2017,(18):63-67.
[ 8 ] 刘艳萍.基于估时作业成本法的农产品物流作业动因分析框架[J].财会月刊,2015,(06):59-63.
【基金项目】 山西大学商务学院院级科研基金项目“生态文明下绿色物流发展研究——基于成本管理视角”(项目编号:2017001)和“新时代高铁制造业质量成本管控研究”(项目编号:2019001)阶段性成果。
