王利波，徐瑰瑰

（凯里学院，贵州凯里 556011）

0 引言

近年来，相互干扰的食饵-捕食模型吸引了许多学者的关注[1-6]，其模型由Hassell[6]在1971年引入的，形式为：

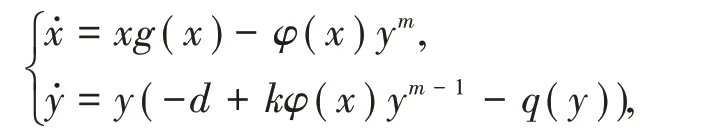
其中，x,y表示食饵，捕食者的人口密度，0＜m＜1为相互干扰系数.

现实中，由于模型的瞬时变化，使得脉冲系统能更加真实反映物种间的关系，所以，在文献［7］中，作者研究了如下系统的持久性和全局吸引性：

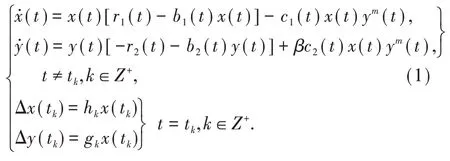
在上述系统的基础上，在文献［8］中，Wang等引入了时滞，使得系统变为：

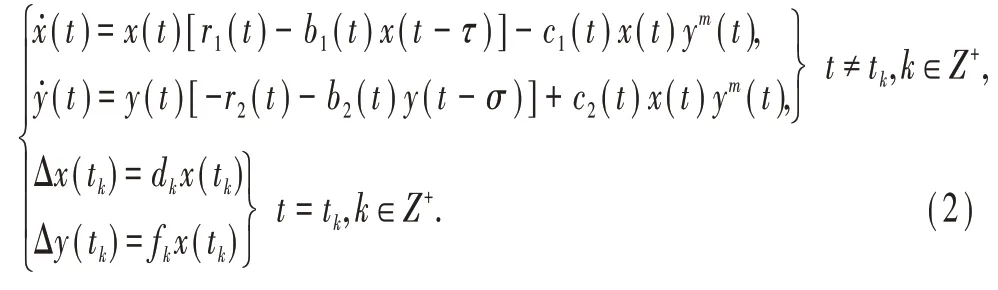
作者研究了系统（2）的周期解、持久性和全局吸引性.但是，我们注意到在文献［7-8］中假设脉冲条件满足：（F）-1＜dk≤0,-1＜fk≤0.显然，这是不合理的.另外，由于环境随季节呈现的是非严格意义上的周期性变化，概周期性变化对描述自然界的变化规律更为准确；因此，建立概周期生态系统对种群动力学行为进行研究更具有现实意义.因此，本文的目的之一是改变条件（F），研究如下系统的持久性及概周期解：

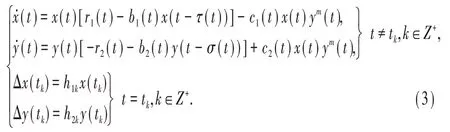
其中，hik,i=1,2表示食饵、捕食者在t时刻的脉冲作用，脉冲时刻tk满足0=t0＜t1＜t2＜…,且=+∞，序列集,j∈Z为一致概周期的.在本文中我们假设hik＞-1,i=1,2.ri(t),bi(t),ci(t),τ(t),σ(t),i=1,2为非负连续概周期函数有界函数.显然，系统（1）、（2）是系统（3）的特殊情况.

1 预备知识

设Rn是n维欧式空间，定义范数||x||=令I=，用I表示关于距离是无界且严格单增的所有序列集.令引入以下记法：

PC(ξ0)为以点μ1,μ2,…∈[ξ0-ζ,ξ0]为第一类间断点且在这些点左连续的函数φ:[ξ0-ζ,ξ0]→Ω的全体.

对于J⊂R，PC(J,R)为J→R2上以点tk为第一类间断点且左连续的分段连续函数的全体.

令φ,φ∈PC(0)，记x(t)=x(t;0,φ),y(t)=y(t;0,φ),x,y∈Ω为系统（3）满足如下初值条件的解：

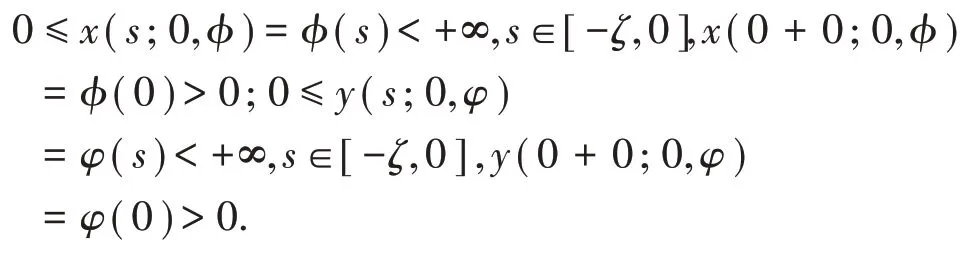
设T,P∈I,s(T⋃P):I→I为使得s(T⋃P)是一个严格增序列的映射；若D⊂R且ε＞0，则θε(D)={t+ε:t∈D},Fε(D)=⋂{θε(D):ε＞0}.

记φ=(φ(t),T)为空间PC×I的元素，对于实数序列{}αn，令θαnφ={φ(t-αn),T-αn}⊂PC×I，其中T-αn={tk-αn:k∈Z,n=1,2,…}.

定义1[9]称序列是一致概周期的，若对∀ε＞0，存在任何序列的ε-概周期的相对稠密集.

定义2[9]函数φ∈PC(R,R)被称为概周期函数是指：

（2）对∀ε＞0,∃δ＞0使得若t′和t″属于φ(t)的同一个连续区间，当|t′-t″|＜δ时，有|φ(t′)-φ(t″)|＜ε.

（3）对∀ε＞0，存在相对稠密集T，使得若η∈T，有|φ(t+η)-φ(t)|＜ε,∀t∈R,|t-tk|＞ε,k∈Z成立.称T的元素是ε-概周期的.

引理1[9]序列为一致概周期的当且仅当每个无限平移序列{tkαn},k∈Z,n=1,2,…,αn∈R中有一个在I中收敛的子列.

定义3[9]序列φn,φn=(φn(t),Tn)∈PC×I一致收敛到φ,φ=(φ(t),T)∈PC×I当且仅当对∀ε＞0,∃n0＞0使得当n≥n0,t∈RFε(s(Tn⋃T))时，ρ(T,Tn)＜ε,||φn(t)-φ(t)||＜ε一致成立.

定义4[9]称φ∈PC为具有T中第一类间断点的分段连续的概周期函数，若对任一实数序列存在一子列{αn}使得θαnφ在PC×I上是紧的.

引理2[9]令{tk}∈I，则存在一个正整数A，使得对于每个长度为1的区间，序列{}tk的元素个数不超过A，即i(s,t)≤A(t-s)+A，其中i(s,t)是区间(s,t)内点tk的个数.

为方便行文，我们引入以下符号：

其中f(t)是非负有界函数.

2 持久性

引理3[10]假设x∈PC(R)在t=tk,(k∈Z+)处为间断且是左连续的，若

其中，f∈C(R×R,R),Ik∈(R,R),且Ik(x),(k∈Z+)关于x非减.设如下脉冲微分方程在[t0,∞)上存在最大解u∗(t)

则当t≥t0时，由可得x(t)≤u∗(t).

注：如果引理3中不等式反号，u∗(t)系统（4）在[t0,∞)上的最小解，则当t≥t0时，由可得x(t)≥u∗(t).

引理4[11]假设a,b＞0，对于如下脉冲方程：

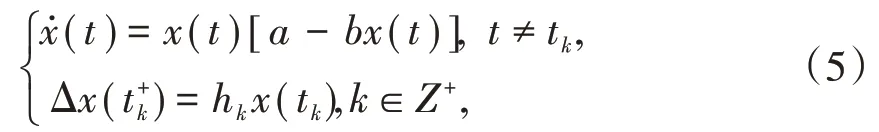
存在唯一全局渐进概周期解x∗(t)，且，其中A如引理2中定义

利用上述引理的证明，不难证明：

引理5假设a,b＞0，对于如下脉冲方程：

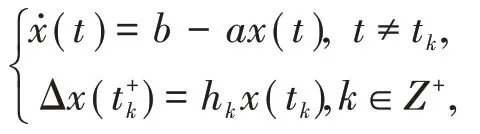
存在概周期解x∗(t)，且

引理6假设a,b＞0,0＜m＜1，对于如下脉冲方程：

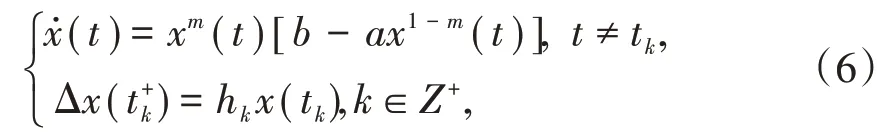
存在概周期解x∗(t)，且

引理7假设a,b＞0，对于如下脉冲方程：

当t≠tk,k∈Z+，考虑区间[t-τ(t),t),t∈(0,+∞)，不妨设t1＜t2＜…＜tj是[t-τ(t),t)内的脉冲点，对不等式（9）从t-τ(t)到t积分，可得

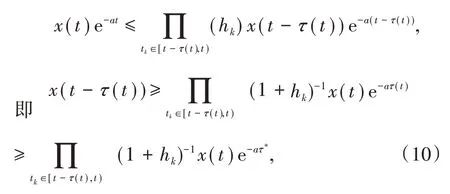
将上式代入（8）式可得

利用引理3和引理4可得结论.

引理8假设a,b＞0,x(t)≤M，对于如下脉冲方程：

证 有假设x(t)≤M，即对于∀ε＞0，存在T＞0，当t≥T，有x(t)≤M+ε.

由（11）式，可得：

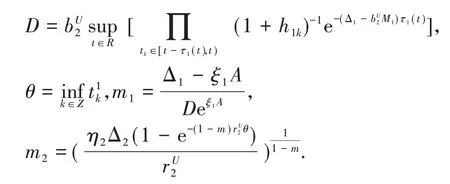
定理1如果(H1)Δ1＞0,Δ2＞0成立，则系统（3）的每个解(x(t),y(t))T都满足m1≤x(t)≤M1,m2≤y(t)≤M2.

证由系统（3）可得

3 全局吸引性

定理2假设定理1成立，并且满足以下条件：(1-σ′(t))＞0，其中τ(t),σ(t)在[0,+∞)上连续可微；

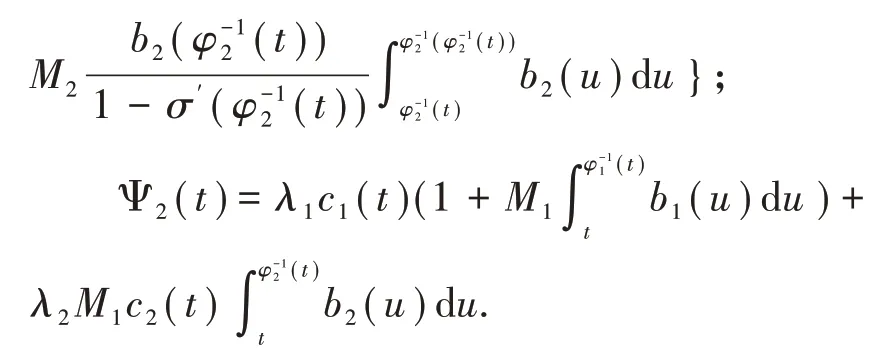
则系统（3）是全局吸引的.

证：若(x(t),y(t))T,((t),(t))T是系统（3）的任意两个正解，由定理1知，存在T0＞0和正常数mi,Mi(i=1,2)，使得：

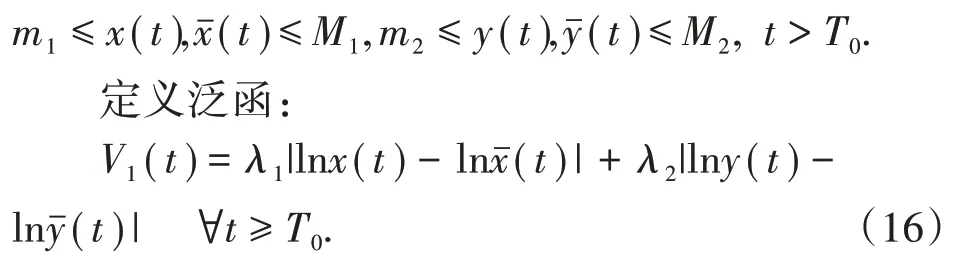
当t≠tk,k∈Z+，由系统（3）的解，计算（16）式的右上导数得

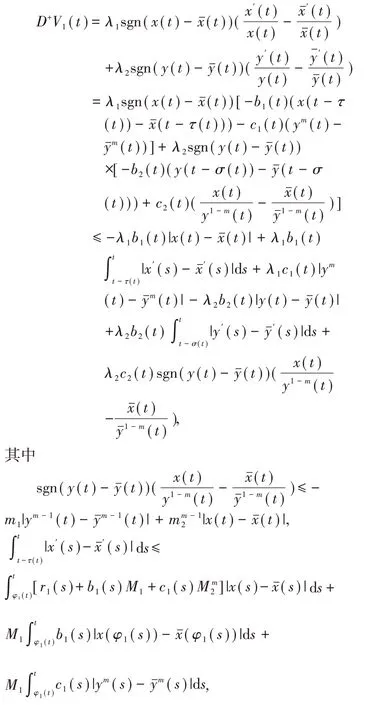
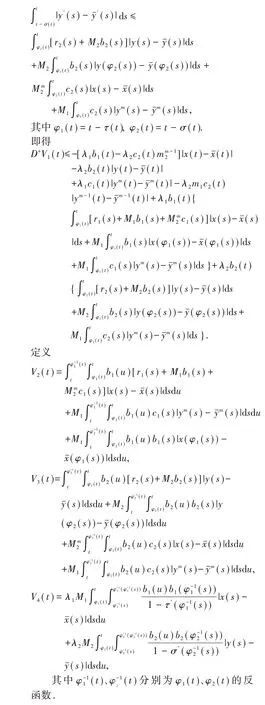
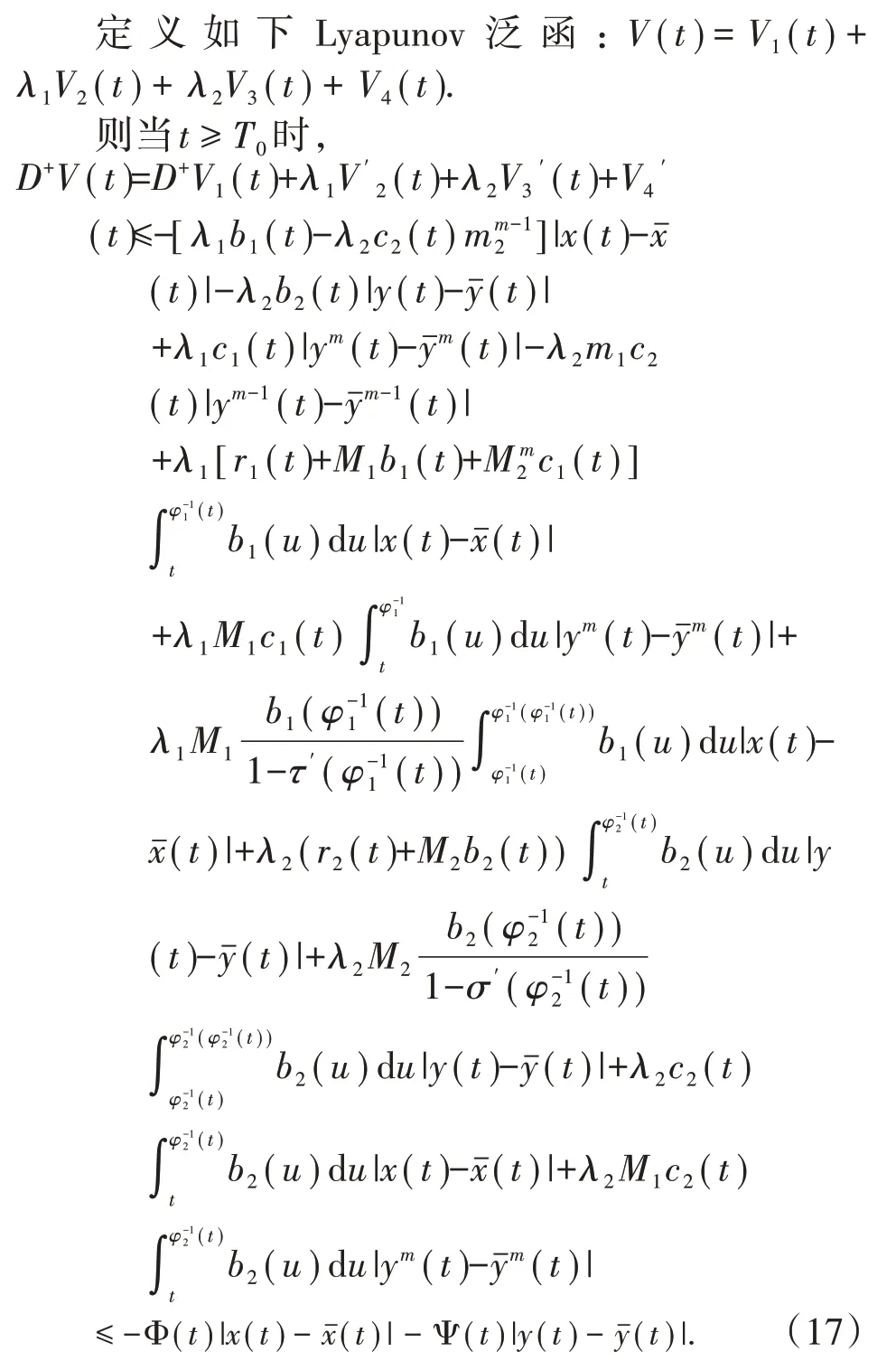
由于（H2）、（H3）可知对足够大的T＞T0，存在正常数p,q使得

即系统（3）是全局吸引的，定理得证.

4 概周期解

令{sn}为任意整数序列，使得当n→∞时，有sn→∞.如有必要取其一子列，对于t∈R有ri(t+

σ(t+sn)→σ*(t).由引理1可知，当n→∞时，序列集{tk-sn},k∈Z关于k∈Z一致收敛到序列

则系统（3）的壳方程为：

由概周期理论，可以得到如果系统（3）满足条件（H1）-（H3），则系统（3）的壳方程（19）同样满足（H1）-（H3）.

由文献［9］中的引理，容易得到如下引理.

引理9若系统（3）的每个壳方程都有唯一严格正解，则系统（3）有唯一严格正概周期解.

引理10若系统（3）满足（H1）-（H3），则系统（3）存在唯一严格正概周期解.

证：由引理9，我们仅需证明系统（3）的每一个壳方程都存在一个唯一严格正解即可.

令xn(t)=x(t+sn),yn(t)=y(t+sn)，对所有t≥-sn+T0,n=1,2,…，使得

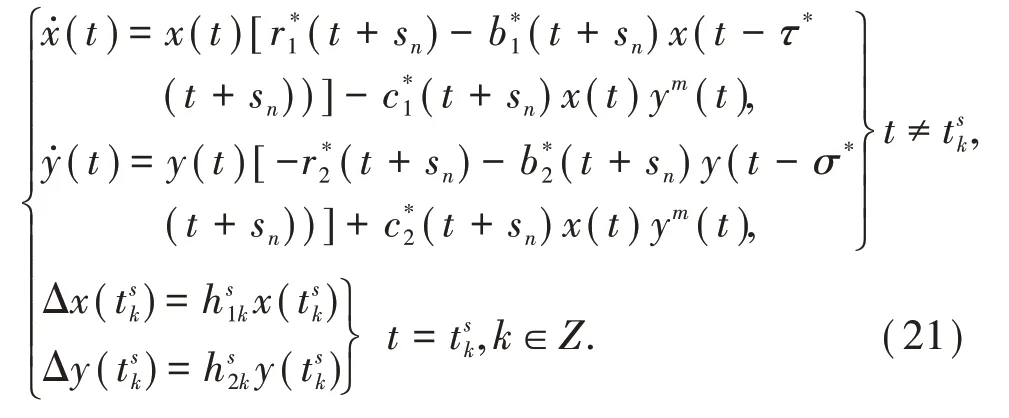
下面证明每一个壳方程（19）严格正解的唯一性.假设壳方程（19）有两个任意严格正解(x(t),y(t))T,(x*(t),y*(t))T，其满足

类似定理2，定义Lyapunov泛函：V*(t)=

其中

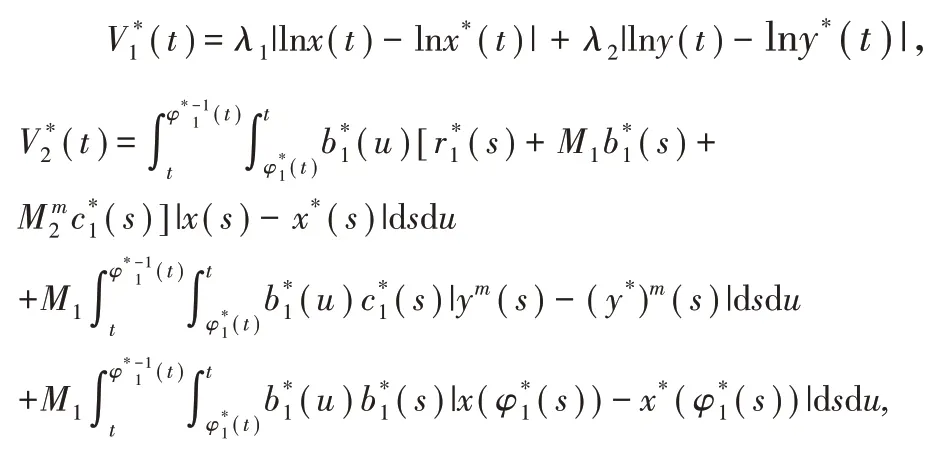
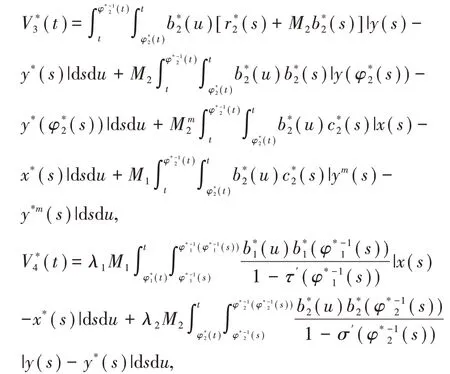
D+V(t)≤-p|x(t)-(t)|-q|y(t)-(t)|,∀t∈R.

上式两端从t到0积分，有

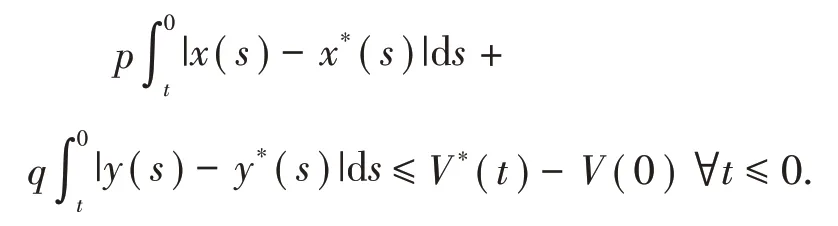
注意到V*是有界的.因此

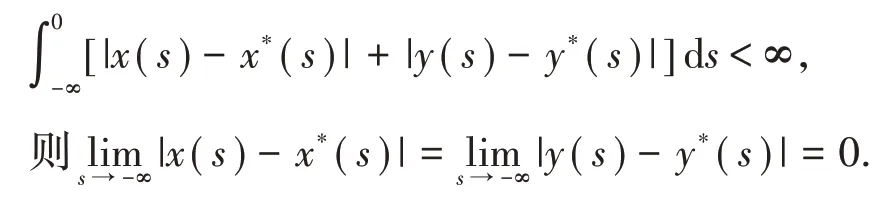
对∀ε0＞0，存在正常数L使得max{|x(t)-x*(t)|,|y(t)-y*(t)|}＜ε0,∀t＜-L.

因此，对∀t＜-L有

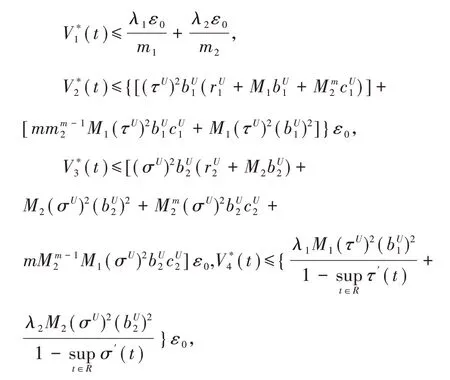
即存在正常数ρ使得V*(t)＜ρε0,∀t＜-L.所以

注意到V*(t)在R上是非增泛函，则V*(t)≡0.即x(t)=x*(t),y(t)=y*(t),∀t∈R.

因此，系统（3）的每一个壳方程都有唯一的严格正解.根据引理9，系统（3）有唯一全局渐进稳定的正概周期解.

由定理2和引理10，可得如下结论.

定理3假设（H1）-（H3）成立，则系统（3）有唯一全局渐进稳定的正概周期解.

注1 定理3给出了系统（3）的全局渐进稳定的正概周期解的充分条件.因此，定理3推广了文献［8］的相应结论.