王雪

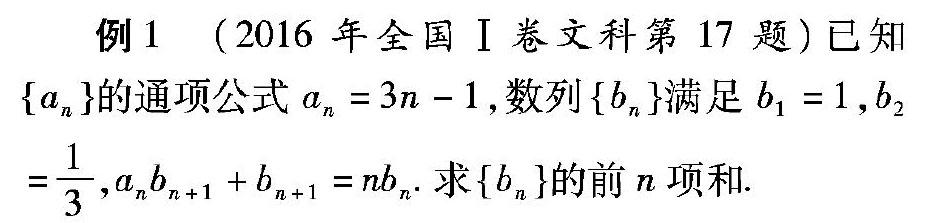
摘 要：数列在高中数学知识体系中的地位极其重要，通过对近几年的高考试题的整理分析，发现数列求和问题在其中扮演着“枢纽”的作用.因此，本文对常见数列求和方法进行整理、分析，并归纳其适用题目所具备的特征.

关键词：高考数学;数列;求和

高考中关于数列求和的考查较为常见，题型的主要方向有正向、逆向（由数列的前n项和求数列的通项公式或其他量）、数列求和与函数（将数列前n项和看作关于n的函数）、不等式综合应用（求取数列和的最值或证明不等式成立）.

数列求和的常用方法有公式法求和、倒序相加法求和、错位相减法求和、裂项相消法求和、分组转化法求和等.在解题中，学生常常分不清何时采用何方法，下面通过几道典型例题，对几种方法的适用特征进行总结.

1 公式法求和

若一个数列是等差数列、等比数列以及由等差数列、等比数列通过加、减运算构成的数列，则其可以使用相应的等差数列或等比数列的公式直接进行求和运算.

例1 （2016年全国Ⅰ卷文科第17题）已知an的通项公式an=3n-1，数列bn满足b1=1，b2=1 3，anbn+1+bn+1=nbn.求bn的前n项和.

分析 此题在判断出该数列为等比数列的基础上，直接应用等比数列的前n项和公式进行计算，属于简单题.解题的关键在于熟练地掌握及应用公式.

解析 因为an=3n-1，所以（3n-1）bn+1+bn+1=nbn.整理，得bn+1=bn 3.

所以数列bn是首项为1，公比为1 3的等比数列.

设bn的前n项和为Sn，则

Sn=1-（1 3）n 1-1 3=3 2-1 2×3n-1.

總结 （1）等差数列前n项和公式Sn=n（a1+an） 2（公式1），Sn=na1+n（n-1） 2d（公式2）在解题时需要根据已知条件决定选用哪个公式更为简便：若已知首项、末项和项数时，则选择公式1;若已知首项、公差和项数时，则选择公式2.

（2）等比数列的前n项和公式

Sn=na1， q=1，a1（1-qn） 1-q=a1-anq 1-q， q≠1.

易错点 在解题时需要对q的取值进行分类讨论.

拓展 由奇数项和偶数项分别构成的等差或等比数列以及等差数列各项的绝对值构成的数列、等差数列的通项乘（-1）n构成的数列可以适用公式法进行数列求和.

2 倒序相加法求和

若一个数列中与首末两项等距离的两项的和相等，则可使用倒序相加法来求此类数列的和.该方法的本质思想是消项.

例2 已知f（x）=x3 1+x3，求f（1 2020）+f（1 2019）+…+f（1）+f（2）+…+f（2020）的值.

分析 由于该式的第一项与最后一项互为倒数，第二项与倒数第二项互为倒数，依次类推.考虑f（x）+f（1 x）的结果，f（x）+f（1 x）=x3 1+x3+1 x3 1+1 x3=x3 1+x3+1 x3+1=1.

解析 令所求式子和为S，则S=f（1 2020）+f（1 2019）+…+f（1）+…+f（2020）.①

S=f（2020）+f（2019）+…+f（1）+…+f（1 2020） .②

两式相加，得2S=1+1+…+14039个

所以S=4039 2.

总结 解决此题的关键是通过观察题目所给的表达式的形式，发现问题的答案（f（x）+f（1 x）=1），此类问题的答案往往在问题之中，我们在解答时要注意从问题入手，之后应用倒序相加法求和.应用倒序相加法求和的步骤是：

（1）令所求式子和为S，S=a1+a2+a3+…+an;

（2）将S的表达式等式右端进行倒置：S=an+an-1+an-2+…+a1;

（3）将以上两式相加得2S，进而求得S的值.

拓展 由此例题我们发现，若能在所给要求和的题目中得到某表达式的和为常数，例如f（x）+f（-x）=c， f（x）+f（1 x）=c，…此种情况下，我们可以应用倒序相加法来解题.

由此可以得出结论：非等差数列也可以使用倒序相加法进行求和[1].

3 错位相减法求和

错位相减法求和适用于an·bn型数列，其中an，bn分别是等差数列、等比数列（即cn=（an+b）qn-1（q≠1））.我们首次接触错位相减法是在推导等比数列的前n项和时，通过错位相减法的应用，可使数列求和计算化繁为简.

例3 （2016年山东高考理科第18题）已知数列an=6n+5，bn=3n+1，令cn=（an+1）n+1 （bn+2）n，求数列cn的前n项和Tn.

分析 此题经过化简后发现是差比型数列，所以我们可以应用错位相减法进行求和计算.

解析 由题意，可知cn=（6n+6）n+1 （3n+3）n=3（n+1）·2n+1.

则数列cn的前n项和Tn=c1+c2+…+cn.

所以Tn=3×[2×22+3×23+…+（n+1）×2n+1].①

2Tn=3×[2×23+3×24+…+（n+1）×2n+2].②

①-②，得 -Tn=3×[2×22+23+24+…+2n+1-（n+1）×2n+2]

=3×[4+4（1-2n） 1-2-（n+1）×2n+2]=-3n·2n+2.

所以Tn=3n·2n+2.

总结 应用错位相减法进行数列求和的步骤是：

（1）写出Tn=c1+c2+…+cn;

（2）等式两边同乘等比数列的公比q，即qTn=qc1+qc2+…+qcn;

（3）将两式作差，转化为等比数列，应用公式进行求和;

（4）两边同时除以1-q，整理得到最后结果.

易错点 在书写过程中，为了准确写出Tn-qTn的表达式，提高解题的准确性，应特别注意将两式“错项对齐”.同时，要对等比数列的公比进行讨论，若q=1，则不能应用错位相减法进行求和.

拓展 学生在应用错位相减法求和时，最大的困难在于最后结果的化简整理.此处将拓展一个公式帮助学生进行计算：形如（An+B）·qn-1型数列求和，其结果为Sn=（αn+β）·qn-β，

其中α=A q-1，β=B q-1-A （q-1）2.（此公式只是验证计算结果的辅助公式，不能写在答题卡上）

4 裂项相消法求和

形如bn=1 anan+1（an为等差数列或an=1 n+k+n）型的数列可使用裂項相消法求和，其基本原理通俗来讲是将数列的某一项拆分为两项或多项，在求和时使前后项能够相互抵消，达到消项化简的目的.

例4 （2017年全国Ⅲ卷文科第17题）若an=2 2n-1，求数列an 2n+1的前n项和.

分析 解决此题的关键是通过对该数列的通项公式的观察发现其分母可拆分，之后将其裂项相抵消.

解析 设数列an 2n+1的前n项和为Sn.

an 2n+1=2 （2n+1）（2n-1）=1 2n-1-1 2n+1.

则Sn=1 1-1 3+1 3-1 5+…+1 2n-1-1 2n+1=1-1 2n+1=2n 2n+1.

总结 在运用裂项相消法求和过程中，要注意以下几个问题：

（1）在利用裂项相消法求和时，要检验裂项前后等式两端是否相等，若不相等，可通过添加系数，使等式的左右两端保持相等;

（2）在利用裂项相消法求和时，我们发现，前后剩余项数是具有对称性的.

拓展 常用的裂项公式：

（1）1 n（n+k）=k（1 n-1 n+k）;

（2）1 （2n-1）（2n+1）=1 2（1 2n-1-1 2n+1）;

（3）1 n（n+1）（n+2）=1 2[1 n（n+1）-1 （n+1）（n+2）];

（4）1 n+n+k=1 k（n+k-n）;

（5）loga（1+1 n）=loga（n+1）-logan.

5 分组转化法求和

此方法是针对一些特殊的数列，从它们的通项公式上来看，既不是等差数列也不是等比数列，但是，若将其拆分开来，可分为几个等差、等比或常见数列.因此，对于这样的数列在进行求和时，应该先将其拆分，之后分别求和，最后将其合并.

例5 （2015年福建高考文科第17题）等差数列an的通项公式为an=n+2，设bn=2an-2+n，求b1+b2+b3+…+b10的值.

分析 解决此题的关键是将该数列的通项公式进行拆分后，发现其是等差数列与等比数列的和，之后分别应用各自的求和公式进行计算求和.

解析 由题意，可得bn=2an-2+n=bn=2n+n.

所以b1+b2+b3+…+b10=（2+1）+（22+2）+（23+3）+…+（210+10）

=（2+22+23+…+210）+（1+2+3+…+10）=2×（1-210） 1-2+（1+10）×10 2=2103.

总结 能够应用分组转化求和法进行求和的数列类型[2]：

（1）an=bn±cn，bn，cn为等差或等比数列;

（2）通项公式为an=bn，n为奇数，cn，n为偶数，bn，cn为等差或等比数列.

6 结论

高考中对于数列知识的考查是必考点，近年来数列在高考中的地位更是突出，数列求和问题的考查频率也很高，但是不难.因此，在平时的教学中，仅仅给出简略的说明是不够的，应该让学生掌握每种方法适用题目所应具有的特征，这样才能“对症下药”，顺利解决数列求和问题.

参考文献：

[1]秦秀红.揭开“倒序相加法”的神秘面纱[J] .中学教研（数学），2008（07）：36-37.

[2]董兴勇.高中数列求和的有效方法初探[J].数学学习与研究，2017（05）：142-143.

（收稿日期：2020-02-17）