倪德果，江 震，杨守志

（汕头大学理学院，广东 汕头 515063）

0 引言

1952年，Duffin和Schaeffer[1]在研究非调和分析问题时，提出了框架的概念.但直到1986年，Daubechies等人的工作才使得人们开始真正地关注到框架理论.框架作为基的推广，由于它的冗余性，使得框架的设计更加地灵活，从而比基能够更好地解决信号处理和传输过程中产生的一些问题，因而框架理论在信号处理，无线通信等领域得到了较为广泛的应用和发展.

经过学者们多年的努力，框架理论取得了丰硕的成果，如：Daubechies和Bin[2]研究了小波框架的典范对偶框架，Gröchenig[3]提出了Banach空间上对偶框架的概念.但借助框架的典范对偶框架去重构信号要涉及到求框架算子的逆算子，通常求逆算子的运算量很大或者无法进行.对于借助于框架的对偶框架重构信号，计算框架的对偶框架也是较为复杂的[4].学者们开始寻求方法去逼近对偶框架，见文献[5-6]，Christensen等[7]人提出了逼近对偶框架的概念和一些构造方法.近年来很多学者也对逼近对偶框架的构造和性质进行了研究，如：Khosravi[8]研究了g-框架的逼近对偶框架，Javanshiri[9]研究了Hilbert空间上逼近对偶框架的一些性质，张伟[10]研究了逼近对偶Hilbert-Schmidt框架等.

本文在第一部分回顾了框架理论的一些基础知识.在第二部分得到了构成逼近对偶框架的一些充分条件和构造方法，首先研究了利用框架的倍数去构造逼近对偶框架.如果是框架，的对偶框架或逼近对偶框架，通过适当的选择实数a，b，之间可构成逼近对偶框架，之间也可构成逼近对偶框架.当U，V是有界线性算子时，之间可构成逼近对偶框架，之间也可构成一对逼近对偶框架.然后研究了通过两个框架的线性组合构造逼近对偶框架，包括框架的两个对偶框架的线性组合，框架和它的对偶框架的线性组合，框架的对偶框架和框架的逼近对偶框架的线性组合，框架的两个逼近对偶框架的线性组合及框架的对偶框架扰动后得到的两个序列的线性组合和原框架之间都可构成一对逼近对偶框架.在第三部分，构造了一些例子.文章中Hilbert空间简记为H，H到H上全体有界线性算子组成的集合简记为B（H）.

1 预备知识

首先回顾一下Hilbert空间中有关框架的基础知识.

定义1.1设是Hilbert空间H上的序列，如果存在常数A，B＞0，对于任意的f∈H，使得

如果{fk}∞k＝1是 Bessel序列，定义 T 是的合成算子，有T算子是线性的，有界的，且.定义 T*是的分析算子，定义S是框架算子，有如果是 Bessel序列，定义U是的合成算子，定义U*是的分析算子，定义V是复合框架算子，有

定义1.2设是Hilbert空间H上的Bessel序列，如果对于任意的f∈H，使得

其中，

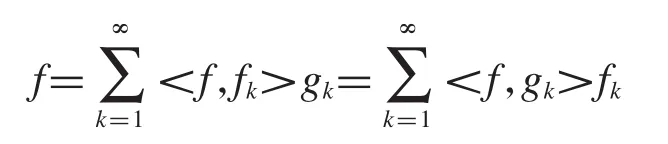
称上式为完美重构.

定义1.3设是Hilbert空间H上的Bessel序列，如果存在0≤ε＜1，对于任意的f∈H，使得

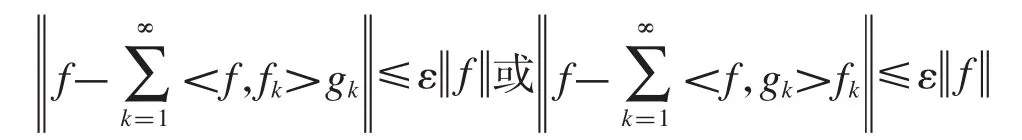
2 逼近对偶框架的充分条件

2.1 利用框架乘以系数构造

在文献[11]中，Azandarani给出了这样的一个论述，设是Hilbert空间中的标准正交基，如果任意实数0＜a＜2，则的逼近对偶框架.当是框架时，a需要满足什么条件，可以构成一对逼近对偶框架.

定理2.1[12]设是Hilbert空间H上的框架，上、下框架界分别为B、A，且A、B＞0，框架算子记为S，如果任意实数那么的逼近对偶框架.

由 Gröchenig[13]91，（1-aB）I≤I-aS≤（1-aA）I.

由于

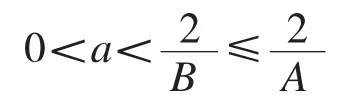
所以

通常显式构造对偶框架的方法[14]159较为复杂，而在定理2.1中，仅通过框架乘以一个系数就构造出了一对逼近对偶框架.我们可以通过调整a，趋于完美重构.当为标准正交基时，我们会发现Azandarani在文献[11]中的论述是该定理的一个推论.我们可以看到Christensen在文献[7]和Javanshiri在文献[9]中的论述也是该定理的推论.

推论2.2设是 Hilbert空间的框架，B、A 是的上、下框架界，则是的逼近对偶框架.

推论2.3设是Hilbert空间中的框架，上框架界为M，则的逼近对偶框架.

定理2.4设任意非零实数0＜ab＜2，设是Hilbert空间中的框架，上、下框架界分别为B，A，的对偶框架，则是一对逼近对偶框架.

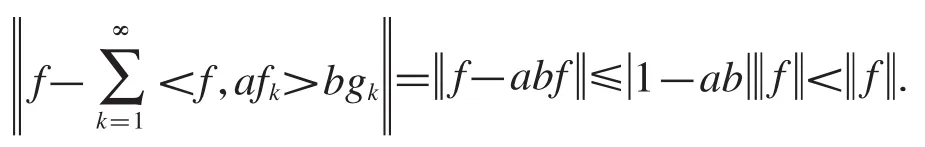
由于对偶框架是逼近对偶框架的特殊情况，于是当ab＝1时，得到构成一对对偶框架.

推论2.5在定理2.4的条件下，当ab＝1时，是一对对偶框架.

定理2.6设任意非零实数a，b，且ab＝1，是 Hilbert空间中的框架，的逼近对偶框架，则是一对逼近对偶框架.

定理2.7设是Hilbert空间中的框架，的对偶框架，U、V∈B（H），且，则是一对逼近对偶框架.

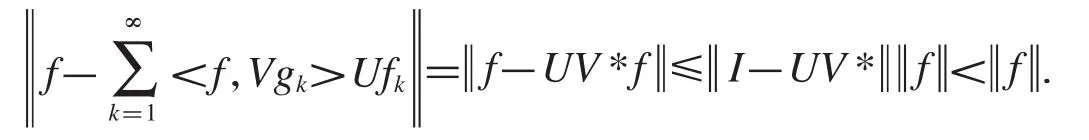
推论2.8设是Hilbert空间中的标准正交基，U、V是B（H）中的可逆算子，当，则是Riesz基，并且构成一对逼近对偶框架.

推论2.9设是Hilbert空间中的标准正交基，U、V是B（H）中的满射算子，当，则是框架，并且构成一对逼近对偶框架.

我们通过Hilbert空间中的标准正交基和有界线性算子，构造出了一对逼近对偶Riesz基和逼近对偶框架.

定理2.10设是 Hilbert空间中的框架，的逼近对偶框架，V 是和的复合框架算子，U是B（H）中的一个酉算子，且U*和V可交换，则和是一对逼近对偶框架.

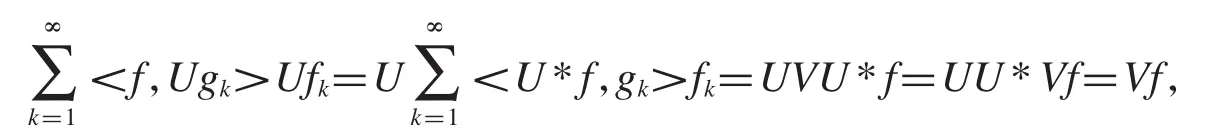
定理2.11设是 Hilbert空间中的一对逼近对偶框架，U、V∈B（H），a，b是非零实（复）数，当U＝aI，V＝bI时，是一对逼近对偶框架等价于和是一对逼近对偶框架.

2.2 利用两个框架的线性组合构造

这一部分我们将研究通过两个框架的线性组合构造逼近对偶框架，首先研究地是通过两个对偶框架的线性组合去构造逼近对偶框架.

定理2.12设任意非零实数是 Hilbert空间中的框架，的两组对偶框架，hk＝agk＋bg'（kk＝1，2，3，…），如果0＜a＋b＜2，则是一对逼近对偶框架.

证明 由题意得，

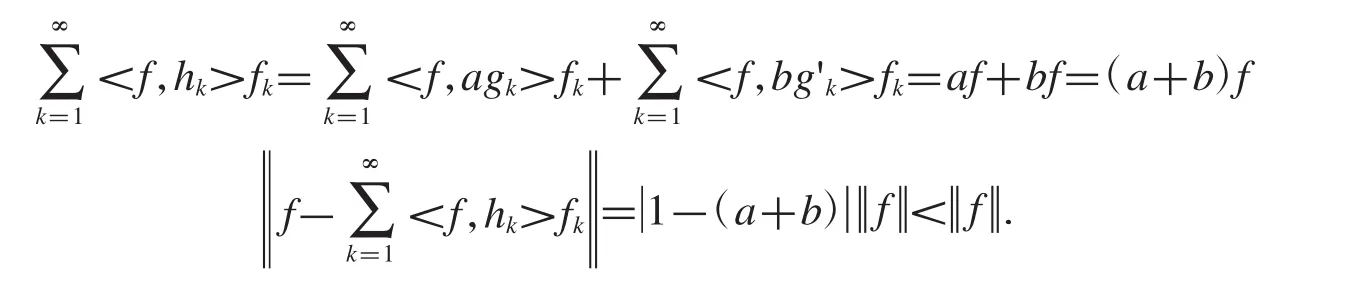
由于对偶框架是逼近对偶框架的特殊情况，所以当a＋b＝1时，我们得到框架和它的两组对偶框架的线性组合之间构成是一对对偶框架.

推论2.13在定理2.12的条件下，如果a＋b＝1，则是一对对偶框架.

定理2.14设是Hilbert空间中的框架，框架算子记为S，的对偶框架，hk＝fk＋g（kk＝1，2，3，…），且满足S＜1，则是一对逼近对偶框架.证明 已知是 Hilbert空间中的框架，易知是 Hilbert空间中的 Bessel序列.

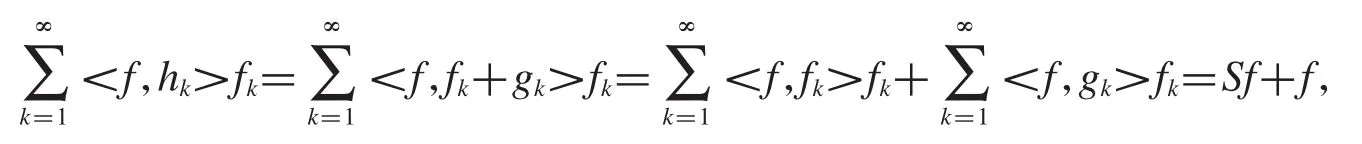
定理2.15设是 Hilbert空间中的框架，的对偶框架，的逼近对偶框架，hk＝gk＋g'（kk＝1，2，3，…），则是一对逼近对偶框架.

定理2.15的证明过程与定理2.14类似，这里不再赘述.在逼近对偶框架的定义中，我们把ε不妨看成趋于完美重构的误差上限，这样得到了下面两个定理.

定理2.16设是 Hilbert空间的框架，的两个逼近对偶框架，ε0记为关于的趋于完美重构的误差上限，ε1记为关于的趋于完美重构的误差上限，且满足 ε0＋ε1＜2，则是一对逼近对偶框架.

证明

定理2.17设a，b是非零实（复）数，是 Hilbert空间的框架，的两个逼近对偶框架，V1记为的复合框架算子，V2记为的复合框架算子，ε0记为关于的趋于完美重构的误差上限，ε1记为关于的趋于完美重构的误差上限，且满足，则是一对逼近对偶框架.

证明

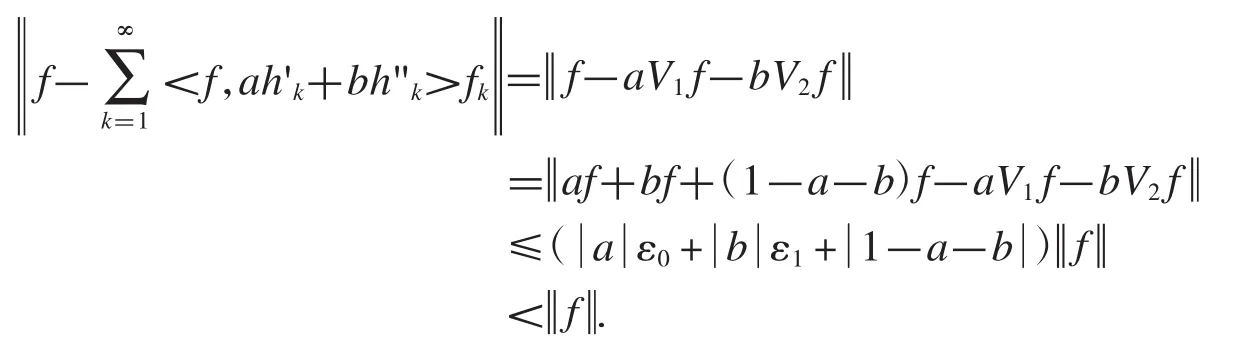
定理2.18设是Hilbert空间的框架，上、下框架界为A，B，的对偶框架，上框架界为是Hilbert空间中的序列，如果存在常数对于任意的有限序列{ck}，使得

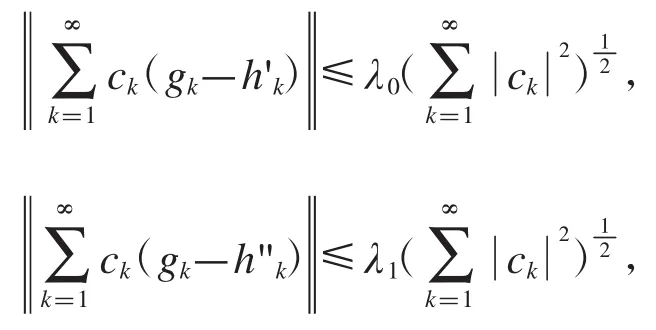
成立，对于任意的f∈H，则有

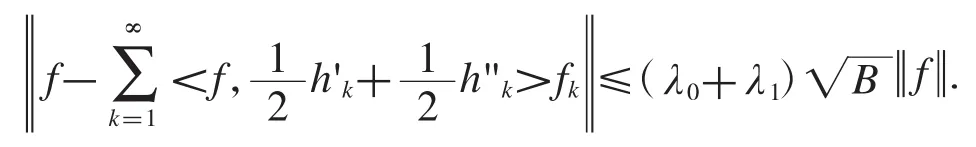
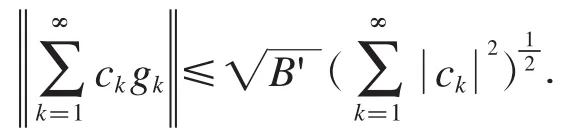
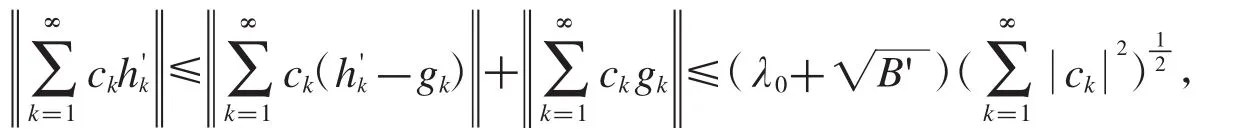
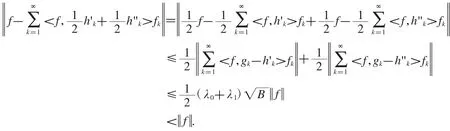
3 例子

这一部分，我们给出了关于前面的部分定理的一些例子，并且我们发现可以通过调整a，b的取值，去趋于完美重构.

考虑H＝C2，标准正交基为{e1，e2}，令

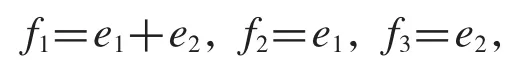
例3.1构造关于定理2.1的例子，取，计算验证得，的逼近对偶框架，且求得的ε不同，这也表明我们可以通过选择适当的a趋于完美重构.

例3.2构造关于定理2.4和推理2.5的例子，通过计算得，其典范对偶框架为

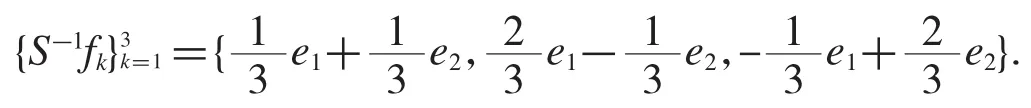
例3.3构造关于定理2.12和推论2.13的例子，通过文献[14]159的方法，我们构造出了的一个对偶框架为取另一个对偶为当取验证得构成一对逼近对偶框架.当取，验证得构成一对对偶框架.